Методичка РГР 4. Задание 4 расчет переходных процессов в электрических цепях

• Название: Задание 4 расчет переходных процессов в электрических цепях
• Дата: 24.04.2022
• Размер: 2.22 Mb.
• Имя файла: Методичка РГР 4.doc
• Тип: Документы; #492766
• страница: 4 из 5

Расчет переходного режима
с помощью интеграла Дюамеля

В соответствии с п. 4 и данными карточки задания исходная схема преобразуется в схему рис. 4.43. При этом требуется определить переходный ток i₅(t).

Рекомендуемый порядок расчета следующий.

1. 
   Записать формулу Дюамеля в общем виде
   

.

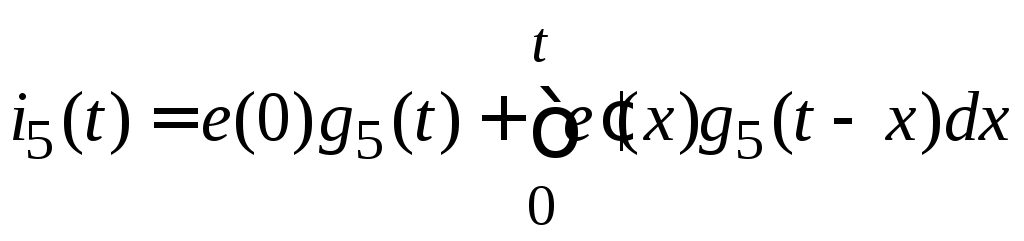2. Найти переходную проводимость g₅(t) для исследуемой цепи, принимая во внимание, что g₅(t) численно равно переходному току i₅(t) в схеме рис. 4.43 при замене e₅(t) на постоянную эдс величиной 1 В. При этом определение может выполняться классическим или операторным методами расчета переходных процессов.

3. 
   Определить g₅(t – х), для чего достаточно заменить в формуле g₅(t) величину t на (t – х).
   

4. Рассчитать для каждого временного интервала функции e(t). Для этого необходимо найти производную по времени t от заданного закона e(t) для каждого временного интервала, а затем в полученных выражениях заменить t на х.

5. Подставить найденные величины в формулу Дюамеля и записать искомую величину с помощью этой формулы для каждого временного интервала заданной функции e(t).

Ниже приводится пример записи произвольного тока i(t) в общем виде с помощью формулы Дюамеля для графика e(t), показанного на р


Рис. 4.45
ис. 4.45. Следу­ет обратить вни­мание на правиль­ность подстанов­ки пределов ин­тегрирования и учета скачков для каждого временного интервала e(t). Из рис. 4.45 видно, что e(t) изменяется во времени по сложному закону. Начальное значение эдс e(0)= E₀.
В интервале от t = 0 до t = t₁ эдс плавно растет, а закон ее изменения в этом интервале времени e₁(t). В момент t = t₁ она меняется скачком от значения e_a до значения e_b, затем снова изменяется по другому законуe₂(t). В интервале времени от t = t₂ до t = t₃ эдс во времени не изменяется. При t = t₃напряжение скачком уменьшается от значения e_c = e_d до нуля.

Пусть требуется найти ток в пределах каждого из приведенных интервалов времени. Под первым интервалом будем понимать интервал от t = 0 до t = t₁ (не включая скачок эдс от e_a до e_b); под вторым от t₁ до t₂, включая скачок от e_a до e_b; под третьим от t₂ до t₃ (не включая скачок от e_d до нуля); под четвертым интервалом будем понимать время при t > t₃, включая скачок от e_dдо нуля.

Интегрирование проводим по х, понимая под t фиксированный момент времени, в который требуется найти ток. Ток в любой момент времени t определяется действием всех эдс, вступивших в действие к этому моменту.

В первый интервал времени (0 ≤ t ≤ t₁)

.

Во второй интервал времени (t₁ ≤ t ≤ t₂)

.

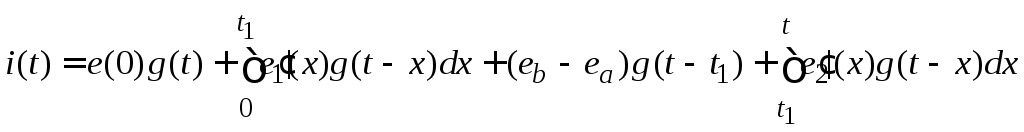Слагаемое (e_b – e_a)g(t – t₁) обусловлено скачком напряжения от e_a до e_b в момент времени t₁.
В третий интервал времени (t₂ ≤ t ≤ t₃)



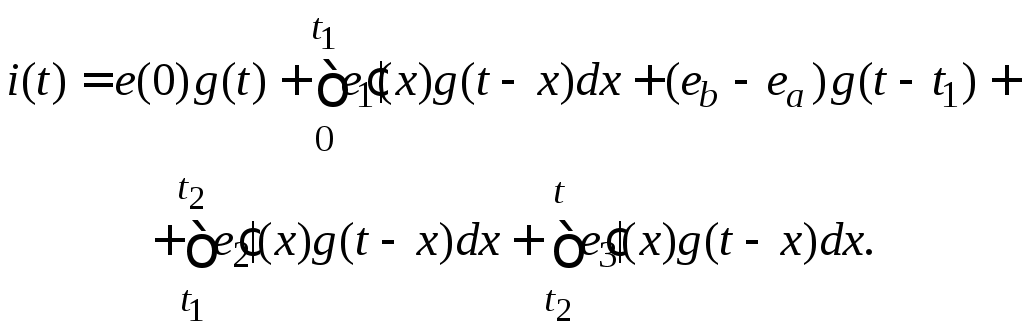
Очевидно, что последний интеграл в выражении для i(t) в рассматриваемом интервале будет равен нулю, так как , поскольку в этом интервале эдс не зависит от t.

В четвертом интервале времени (t > t₃)