|
|
Методичка РГР 4. Задание 4 расчет переходных процессов в электрических цепях
Графики входных эдс (к п. 4 задания) 

УКАЗАНИЯ К РАСЧЕТУ
Классический метод
К резистивной части любой неоднородной цепи применимы методы преобразований, известные из теории цепей постоянного тока. Поэтому если возможно послекоммутационную схему рекомендуется упростить, за счет сведения цепи, не содержащей реактивных элементов, в одну эквивалентную ветвь. Например, на рис. 4.1 показана исходная схема, в которой после коммутации (замыкания ключа) сохраняется три контура. С учетом равнопотенциальности узлов 1 и 2 параллельные резистивно-активные ветви (вторая и пятая) могут быть преобразованы в одну эквивалентную активную ветвь с параметрами Eэ и Rэ. При этом послекоммутационная схема принимает вид, представленный на рис. 4.36. Параметры эквивалентной ветви:
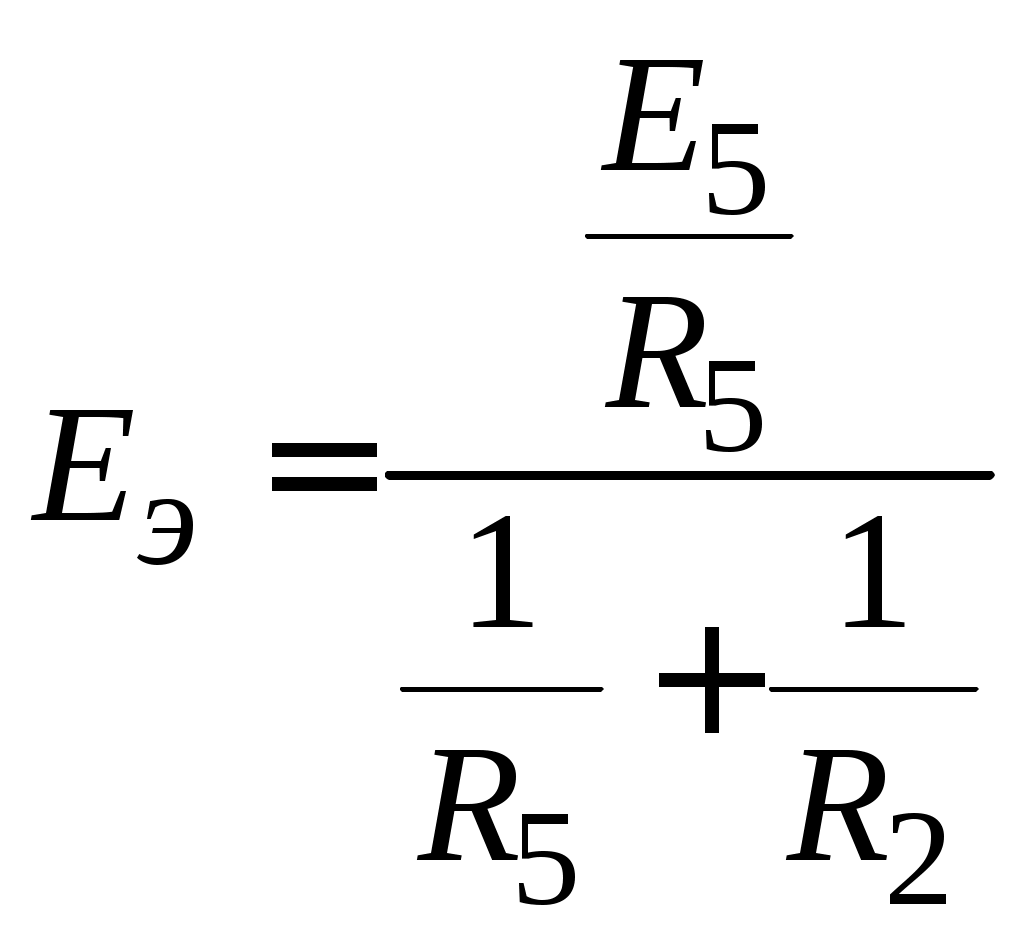 , , 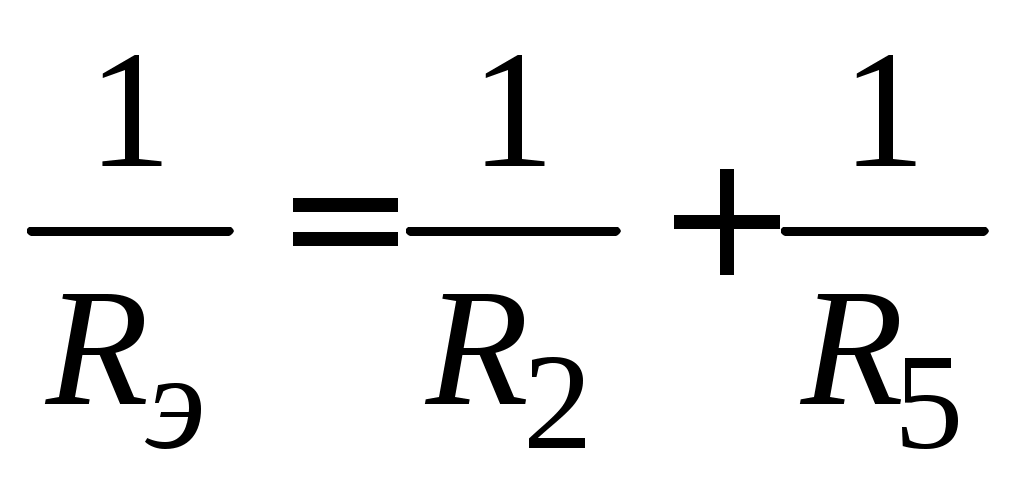 . .
Первый пункт задания предусматривает расчет переходного процесса в схеме классическим методом. В соответствии с рассматриваемым примером для п. 1 индивидуальной карточки переходный процесс имеет апериодический характер, а искомой величиной является переходный ток i6(t).
Рекомендуемый порядок расчета следующий.
1. Записать общее решение для искомого тока (напряжения).
Например,
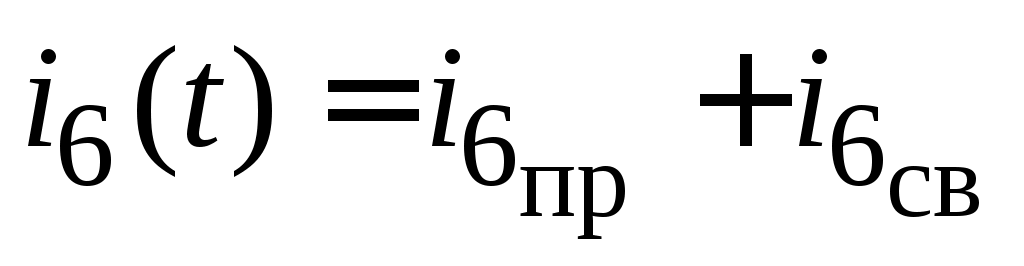 . (4.1) . (4.1)
2. Определить принужденную составляющую искомой величины. Для этого необходимо в послекоммутационной схеме в установившемся режиме (t = ∞) выполнить расчет i6пр любым из известных методов расчета цепей постоянного тока. Так как в схеме (рис. 4.36) действует постоянная во времени ЭДС Eэ, то  и и 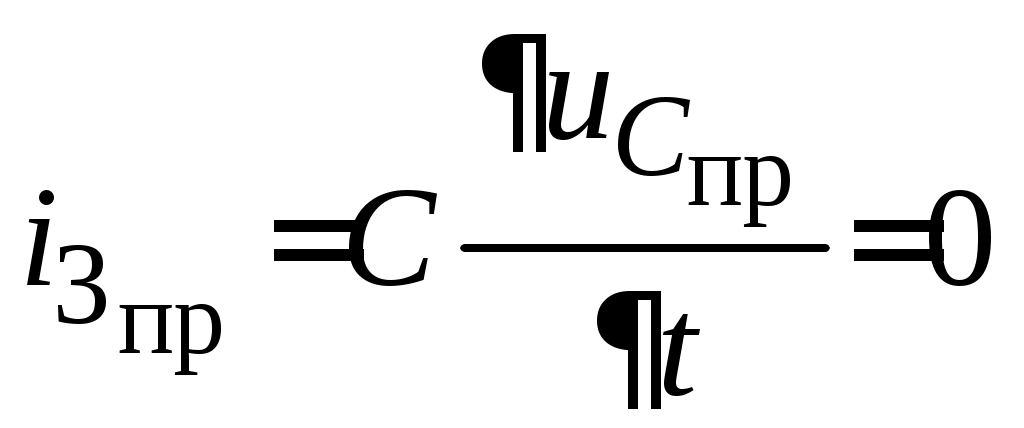 . .
 
Рис. 4.36 Рис. 4.37
Расчетная схема для определения принужденных составляющих при Eэ = constпоказана на рис. 4.37. Очевидно, что для рассматриваемой схемы
 . .
Если в соответствии с требованиями карточки задания требуется определить  (напряжение в разрыве), достаточно составить уравнение по второму закону Кирхгофа для любого контура, включающего искомое напряжение, например, (напряжение в разрыве), достаточно составить уравнение по второму закону Кирхгофа для любого контура, включающего искомое напряжение, например,
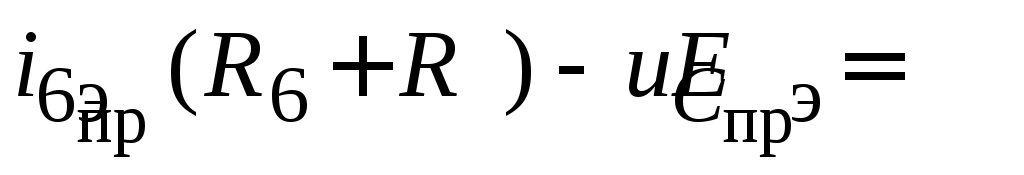 , ,
и найти  после предварительного определения необходимых токов в ветвях. после предварительного определения необходимых токов в ветвях.
3. Записать в общем виде выражение для свободной составляющей искомой величины. Для реализации п. 3 следует иметь в виду, что в общем случае свободная составляющая представляет собой сумму слагаемых, число которых определяется числом корней характеристического уравнения, а вид этих слагаемых зависит от вида корней характеристического уравнения. Поэтому прежде всего следует составить характеристическое уравнение для послекоммутационной цепи и определить его корни.
Характеристическое уравнение можно получить, приравняв нулю главный определитель системы алгебраизированных уравнений, составленных по методу контурных токов для свободных составляющих в послекоммутационной схеме. Контуры рекомендуется выбирать так, чтобы в каждом из них было минимум реактивных элементов. Так, для схемы рис. 4.36 (выбранные контуры обозначены пунктирными линиями) после представления индуктивного сопротивления как Lp,а емкостного как 1/pC, приравнивая нулю главный определитель системы уравнений, получим
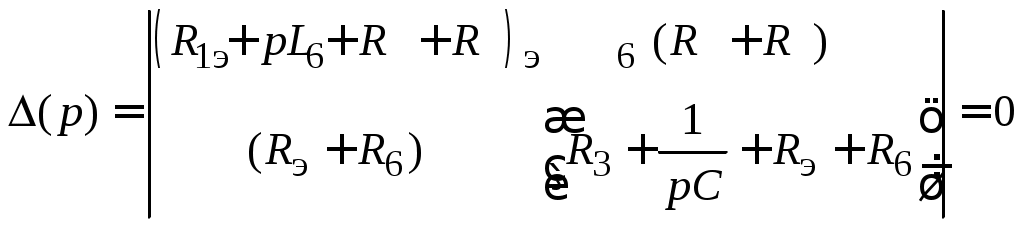 . .
Это уравнение следует привести к виду
p2 + Bp + Q = 0. (4.2)
В случае когда значение емкости взято из карточки для апериодического процесса (С = Са), в результате решения уравнения (2) должны получиться два действительных и различных корня p1 и p2. При этом p1 < 0, p2 < 0. Для колебательного процесса (когда С = Ск) p1,2 =
= – ± jщ0.
Аналитические выражения для свободных составляющих в зависимости от числа и характера корней характеристического уравнения представлены в табл. 4.1.
Т а б л и ц а 4.1
№ п/п
|
Число и характер
корней
|
Характер переходного процесса
|
Вид свободной
составляющей
|
1
|
p1 < 0
|
Апериодический
|
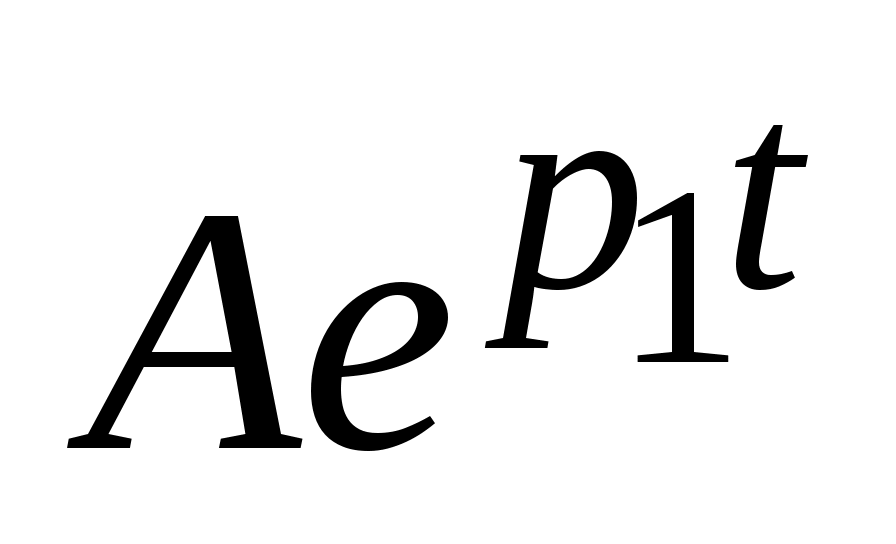
|
2
|
p1 ≠ p2; p1 < 0;
p2 < 0
|
Апериодический
|
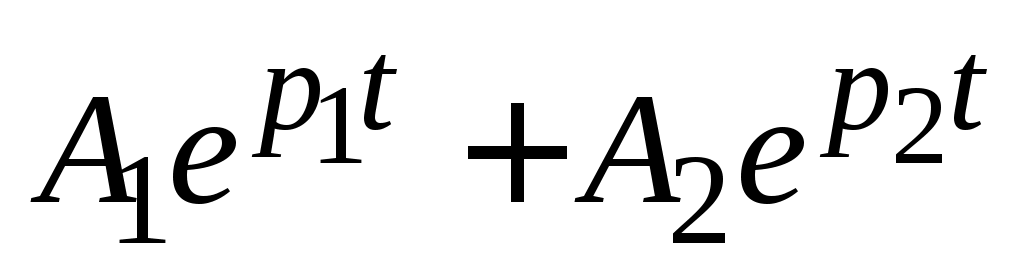
|
3
|
p1,2 = – ± jщ0
|
Колебательный
|
Ae–tsin (щ0t + ш)
|
4. Записать общее решение для искомого тока (напряжения) с учетом известных корней характеристического уравнения. Для рассматриваемого примера в случае апериодического процесса
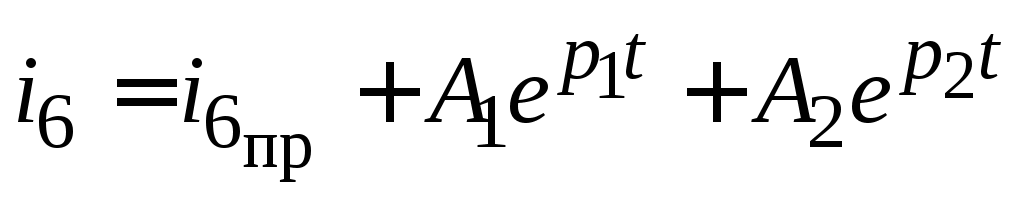 , (4.3) , (4.3)
в случае колебательного процесса
 . (4.4) . (4.4)
С целью последующего определения постоянных A1,A2 для апериодического процесса и A,ш для колебательного необходимо найти значение искомой функции  и ее производной и ее производной  в начальный момент переходного процесса, т. е. при t = 0. Запишем уравнения (4.3) и (4.4) для момента времени t = 0. в начальный момент переходного процесса, т. е. при t = 0. Запишем уравнения (4.3) и (4.4) для момента времени t = 0.
Для апериодического процесса
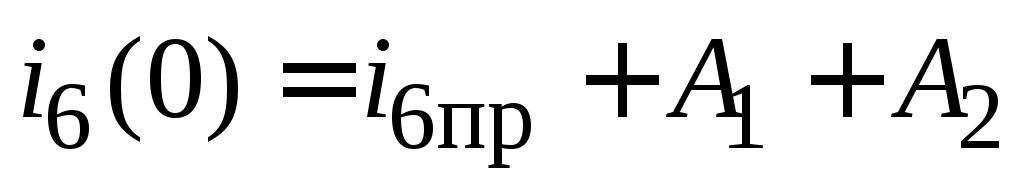 ; (4.5) ; (4.5)
для колебательного процесса
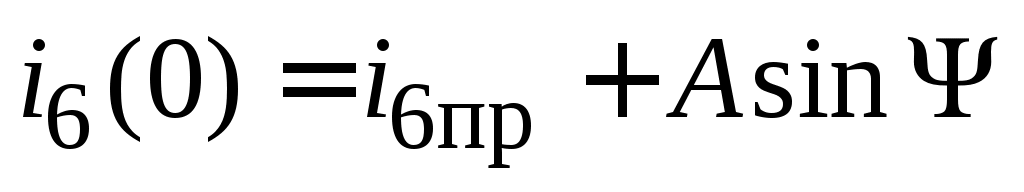 . (4.6) . (4.6)
Дифференцируем выражение (4.3) или (4.4):
 (4.7) (4.7)
или
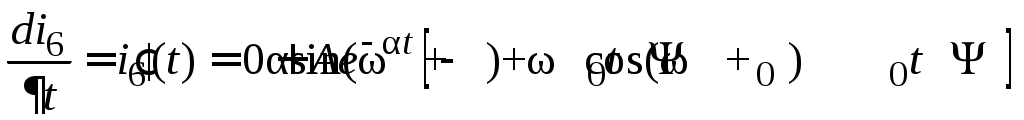 . (4.8) . (4.8)
Рассматривая выражения (4.7) или (4.8) в момент времени t= 0, получим
 (4.9) (4.9)
или
 . (4.10) . (4.10)
Совместное решение уравнений (4.5) и (4.9) для апериодического процесса или (4.6) и (4.10) для колебательного, позволит определить A1 и A2 или Aи ш, если будут известны левые частиi6(0) и 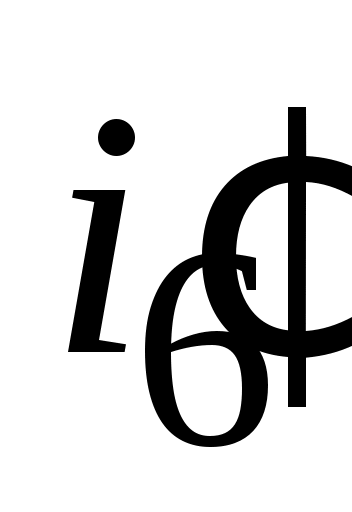 (0)этих уравнений, которые носят названия начальных условий. (0)этих уравнений, которые носят названия начальных условий.
5. Определить независимые начальные условия iL(0) и uC(0) с помощью законов коммутации, согласно которым
iL(0) = iL(– 0); uC(0) = uC(–0). (11)
Значения iL( 0) и uC(0) могут быть найдены в результате расчета цепи в установившемся докоммутационном режиме (t < 0). Схема для расчета независимых начальных условий (c учетом E = const) показана на рис. 4.38. Расчет этой цепи может проводиться с использованием любых методов расчета цепей постоянного тока. В частности, ток в индуктивности до коммутации
 . .
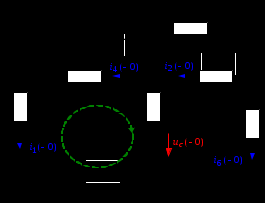
Рис. 4.38
Докоммутационное напряжение на зажимах конденсатора может быть найдено из уравнения, составленного по второму закону Кирхгофа для любого из контуров, включающих в себя искомое напряжение (например, обозначенного пунктирной стрелкой):
 , ,
где 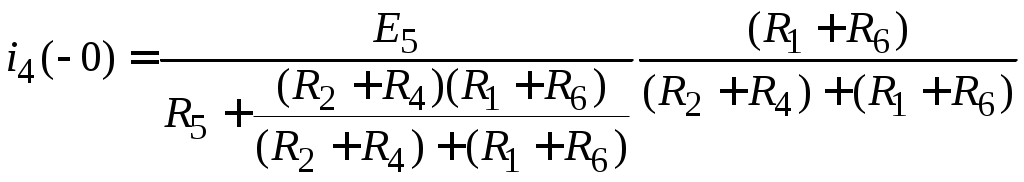 . .
6. Определить зависимые начальные условия. Как известно, зависимыми начальными условиями называют все прочие начальные условия за исключением независимых. Для определения зависимых начальных условий следует составить полную систему уравнений Кирхгофа для мгновенных значений токов и напряжений для исходной схемы в послекоммутационном режиме. Ниже приведены эти уравнения в соответствии со схемой рис. 4.6:
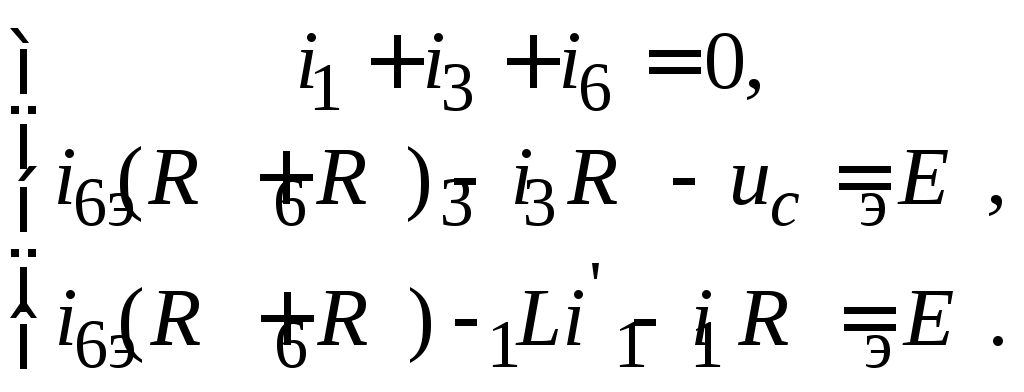 (4.12) (4.12)
Рассмотрим систему уравнений (4.12) для момента времени t = 0
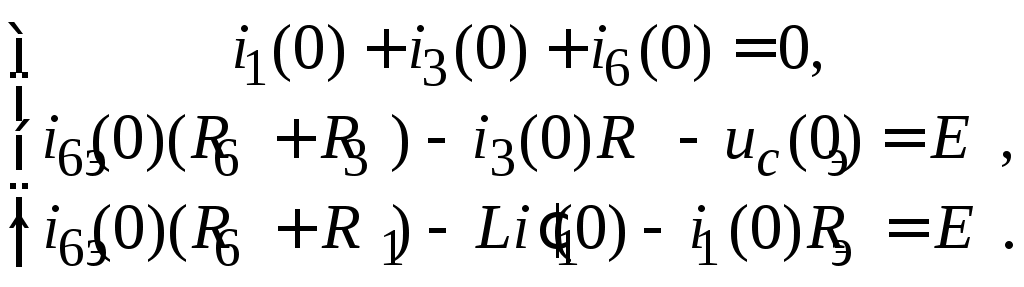 (4.13) (4.13)
Принимая во внимание, что независимые начальные условия i1(0) и uc(0) уже известны (см. п. 5), в системе уравнений (4.13) остаются лишь три неизвестных, которые легко определяются. В частности, находится величина i6(0),представляющая собой левую часть уравнений (4.5) и (4.6). Для определения левой части уравнений (4.9) и (4.10) необходимо исходную систему уравнений (4.12) продифференцировать. В результате чего для t = 0 получим
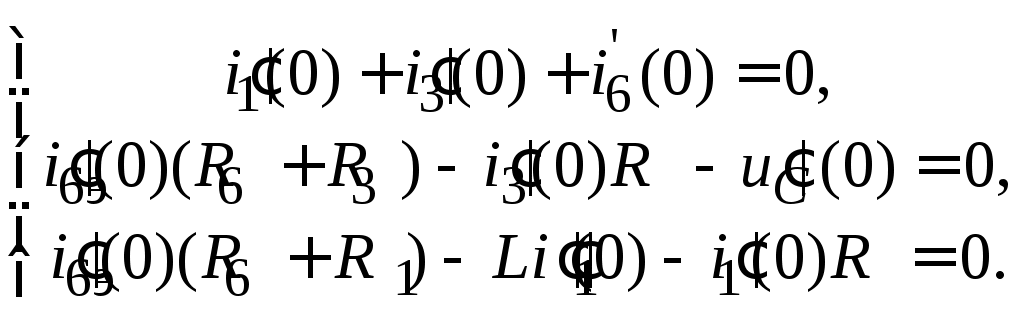 (4.14) (4.14)
Совместное решение систем уравнений (4.13) и (4.14) с учетом того, что
 , (4.16) , (4.16)
позволяет определить производную искомой величины в начальный момент переходного процесса, в частности  , представляющую собой левую часть уравнений (4.9) и (4.10). , представляющую собой левую часть уравнений (4.9) и (4.10).
Таким образом, совместное решение уравнений (4.5) и (4.9) для апериодического процесса или (4.6) и (4.10) для колебательного позволяет определить неизвестные A1и A2 или A и ш, а затем после подстановки их значений в уравнения (4.3) и (4.4) записать окончательные аналитические выражения для искомых переходных токов или напряжений.
Примечание. Если найден ток или напряжение на любом участке преобразованной цепи, с помощью первого и второго законов Кирхгофа можно определить токи и напряжения в любом участке исходной (непреобразованной) цепи.
|
|
|
 Скачать 2.22 Mb.
Скачать 2.22 Mb. .
.
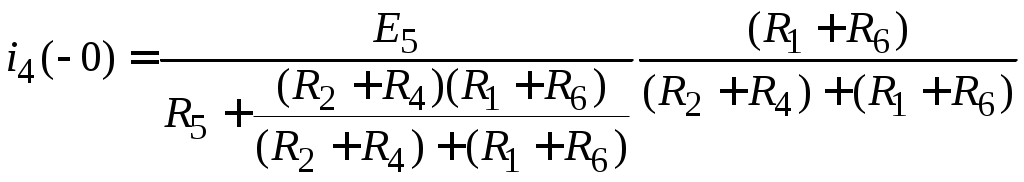 .
.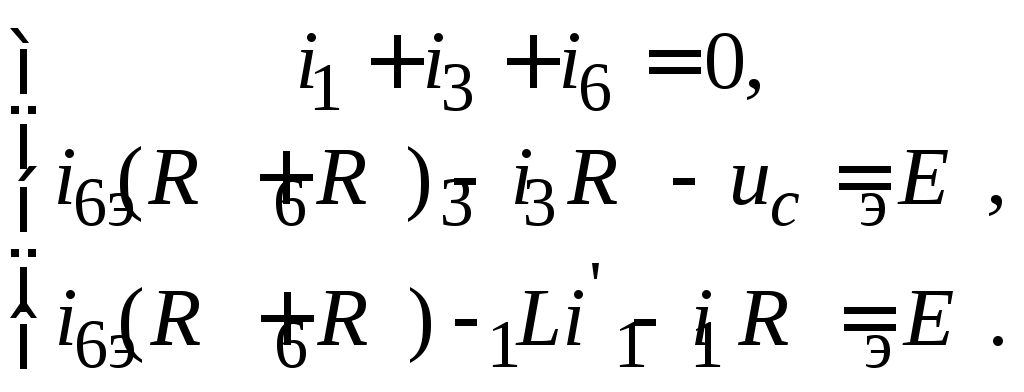 (4.12)
(4.12)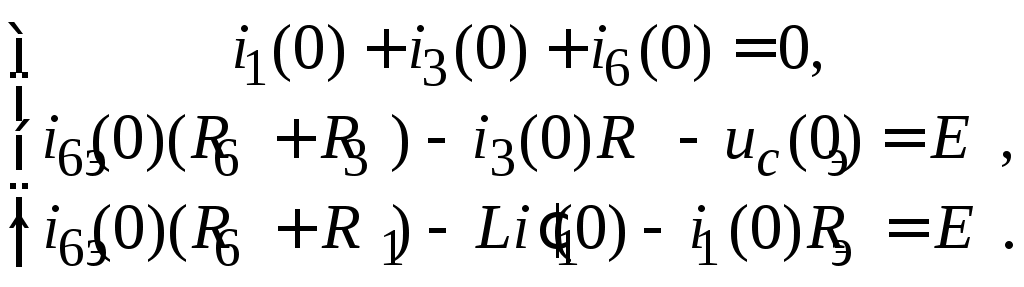 (4.13)
(4.13)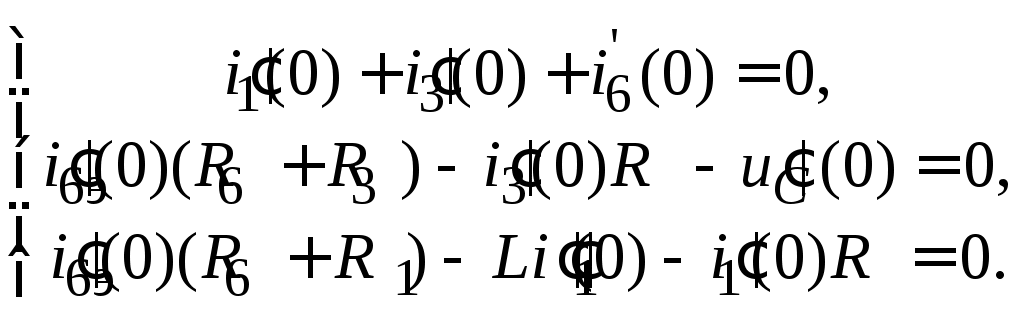 (4.14)
(4.14)


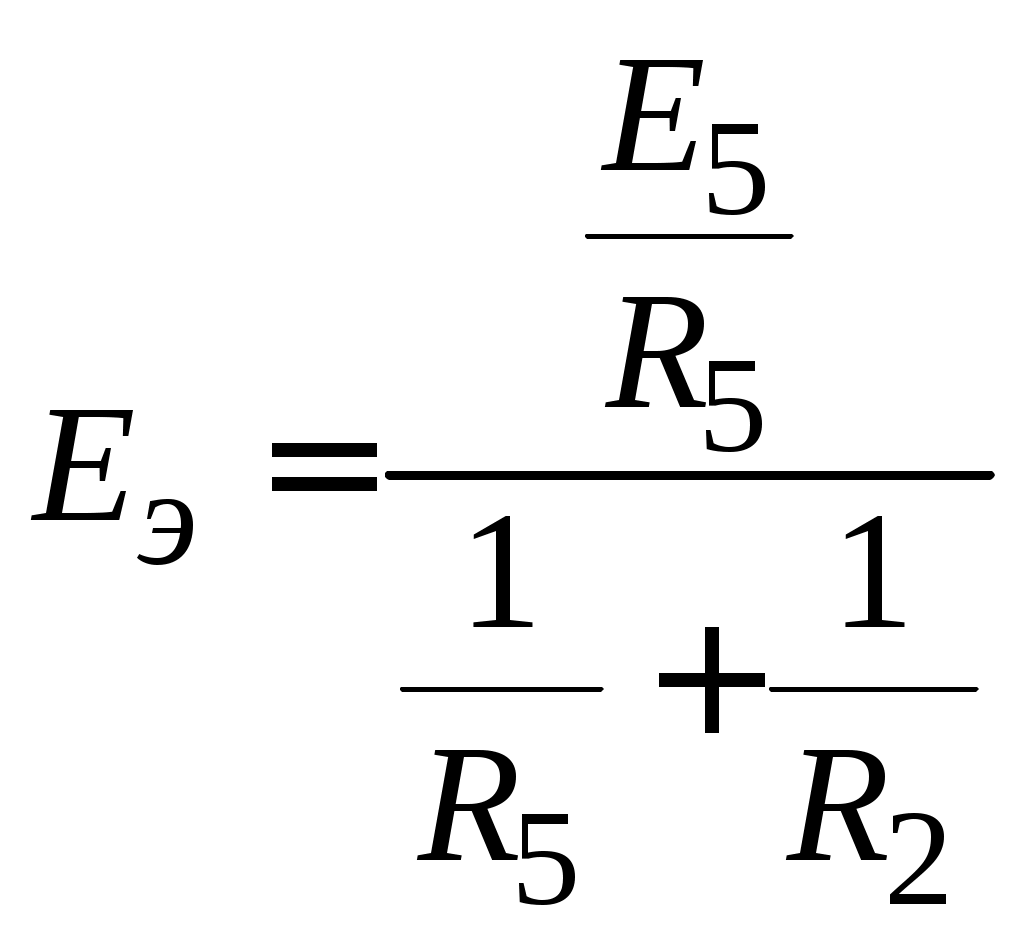 ,
, 

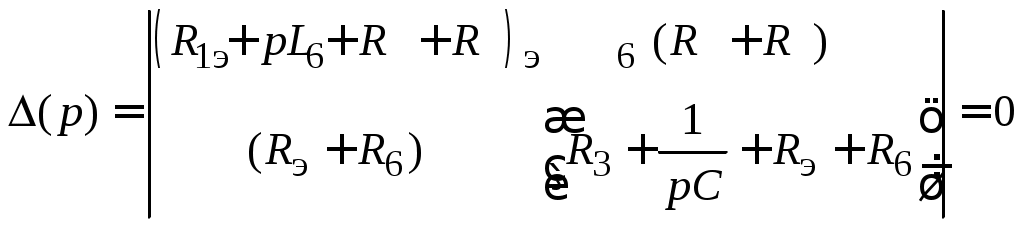 .
.