ИСУ. ИСУ Готовое. Задание Дерево целей и выбор наилучшего решения
 Скачать 315.86 Kb. Скачать 315.86 Kb.
|
|
Задание 1. Дерево целей и выбор наилучшего решения Главному инженеру компании необходимо решить, монтировать или нет новую производственную линию, использующую новейшую технологию. Если новая линия будет работать безотказно, компания получит прибыль 200 млн. рублей. Если же она откажет, компания может потерять 150 млн. рублей. По оценкам главного инженера, существует 6о% шансов, что новая производственная линия откажет. Можно создать экспериментальную установку, а затем уже решать, монтировать или нет производственную линию. Эксперимент обойдется в 10 млн. рублей. Главный инженер считает, что существует 50% шансов, что экспериментальная установка будет работать. Если экспериментальная установка будет работать, то 90% шансов за то, что смонтированная производственная линия также будет работать. Если же экспериментальная установка не будет работать, то только 20% шансов за то, что производственная линия заработает. Следует ли строить экспериментальную установку? Следует ли монтировать производственную линию? Построить дерево целей и привести расчеты и привести расчеты ожидаемой стоимостной оценки Решение Эта задача является типов примером принятия решений в условиях рисков. Мы рассмотрим, как решаются аналогичные проблемы с помощью метода, что, получив название дерево решений. Дерево решение — это графическое отражение проблемы выбора в условиях риска. Отображение возможен альтернатив и их последствий имеет древовидную структуру. Этот метод удобно применять при поэтапная принятии решений. Дерево состоит из ряда узлов и ветвей, что выходят из узлов. Узлы, изображаемые в виде квадратов, обозначают точку Принятие решение, а узлы, изображаемые в видекругов - возможны события. Вдоль ветвей пишут названия альтернатив, их вероятности, платежи за дополнительный информацию. У концов ветвей расставляют платежи. Условные обозначения: А - монтировать производственную линию. Б – создать экспериментальную установку. Q – вероятность события. Дерево строится слева направо, а анализируется наоборот, начиная с конечных ветвей и направляясь к корню. В каждом из узлов-решений выбирается альтернатива (ветвь) с максимальным показателем отдачи, например, самой ожидаемой суммой выигрыша. Если мы хотим использовать принцип максимизации ожидаемой полезности, то надо перенести все промежуточные платежи (в данном случае это плата за монтаж) до конечных ветвей, а затем заменить суммы выигрышей на соответствующие значения полезности. Построим дерево решений.  Рис. 1.1 – Дерево решений Ответ: из дерева решений (рис. 1.1) видно, что если мы не будем создавать экспериментальную установку и сразу смонтируем производственную линию, то мы получим максимальный ожидаемый убыток в размере 10 млн. руб. Если мы создадим экспериментальную установку, то получим в лучшем случае максимальный ожидаемый доход 32,5 млн. руб. Исходя из этого стоит принять решение о создании экспериментальной установки. Задание 2. Дерево целей и выбор наилучшего решения Предприятие занимается перевозками груза. Выиграв тендер на заказ, появилась возможность получить существенную прибыль. Однако собственного транспорта не хватало, что бы вовремя осуществить перевозки. Стоимость работ, в случае их выполнения составляла 50000 т.руб. По условиям договора, в случае своевременного невыполнения заказа предприятию начислялись штрафные баллы, в результате которых терялось половина стоимости (25000 т.руб.) заказа. Для выполнения работ рассматривались два варианта действий: приобрести новые грузовики на сумму 10000 т.р. или отремонтировать транспортные средства, имеющиеся у предприятия, что обойдется предприятию в 4000 т.руб. Экспертная группа определила, что если приобретать новые автомобили, то вероятность их работоспособности на период выполнения работ составляет 90%, а вероятность отказа 10% при этом потери с учетом ремонта и штрафов, составят 10000т.р.. В случае использования отремонтированного собственного парка автомобилей вероятность их работоспособности составляет 60%, а отказа 40% при этом потери от штрафов и ремонта составят 30000т.р.. Выбрать наилучший вариант решения. Построить дерево целей и привести расчеты ожидаемой стоимостной оценки Решение Эта задача является типов примером принятия решений в условиях рисков. Мы рассмотрим, как решаются аналогичные проблемы с помощью метода, что, получив название дерево решений. Дерево решение — это графическое отражение проблемы выбора в условиях риска. Отображение возможен альтернатив и их последствий имеет древовидную структуру. Этот метод удобно применять при поэтапная принятии решений. Дерево состоит из ряда узлов и ветвей, что выходят из узлов. Узлы, изображаемые в виде квадратов, обозначают точку Принятие решение, а узлы, изображаемые в видекругов - возможны события. Вдоль ветвей пишут названия альтернатив, их вероятности, платежи за дополнительный информацию. У концов ветвей расставляют платежи. Условные обозначения: А –приобрести новые грузовики. Б –отремонтировать существующие транспортные средства. Q – вероятность события. Дерево строится слева направо, а анализируется наоборот, начиная с конечных ветвей и направляясь к корню. В каждом из узлов-решений выбирается альтернатива (ветвь) с максимальным показателем отдачи, например, самой ожидаемой суммой выигрыша. Построим дерево решений.  Рис. 1.2 – Дерево решений Ответ: из дерева решений (рис. 1.2) видно, что если мы приобретем новые грузовики, то получим максимальный ожидаемый доход в размере 489т. руб. Если мы отремонтируем существующие транспортные средства, то получим в лучшем случае максимальный ожидаемый доход 284 т. руб. Исходя из этого стоит принять решение о приобретении новых грузовиков. Задание 3. Определение проблем, решение которых даст ощутимый эффект. Предприятие выпускает пластиковую одноразовую посуду. Но в последние полгода наблюдается рост ее себестоимости. Для изучения этого явления была создана специальная комиссия, задачей которой было выяснить причины роста себестоимости. В результате работы комиссии были определены несколько причин, приводящих к росту себестоимости, а также составлена таблица с частотой проявления этих причин.
Построить диаграмму Парето по данным таблицы Определить, какие причины необходимо устранять в первую очередь, что бы был получен максимальный эффект. Решение Перед тем как построить диаграмму Парето необходимо сперва просчитать стоимость причин роста себестоимости. Для этого необходимо умножить столбец (потери от появления причин) на столбец (частота проявления). Получаем следующую таблицу:
После чего необходимо отсортировать причины по убыванию стоимости и просчитать накопительную долю стоимости каждой причины в общей сумме стоимостей причин. Выполнив данные действия получаем следующую таблицу:
После чего приступаем к построению диаграммы Парето и получаем следующий результат:  Ответ: исходя из полученных результатов можно сделать вывод, что необходимо устранить следующие причины роста себестоимости (низкое качество пластика и неисправность оборудования) так как именно на эти причины приходиться 80% потерь. Задание 4. Моделирование системы управления предприятия. Управление автосервисом на первый взгляд задача простая. В то же время эффективность его работы зависит от правильной организации нескольких производственных процессов. Задание. Необходимо разработать модель процессов с использованием модели IDEF0 для небольшого автосервиса: количество машиномест 10, оказываемые услуги – ремонт средней сложности по механике и электрике. Есть приемщик, работа в две смены. Для выполнения задания рекомендуется использовать сведения о работе предприятий автосервиса, включая такие процедуры, как: прием заказа, подготовка к диагностике и ремонту, работы по ремонту или обслуживанию автомобиля, передача отремонтированного автомобиля клиенту, получение оплаты за выполненные работы. Решение IDEF0 — методология функционального моделирования (англ. functionmodeling) и графическая нотация, предназначенная для формализации и описания бизнес-процессов. Основные элементы схемы данной нотации изображены на Рис. 1.3. 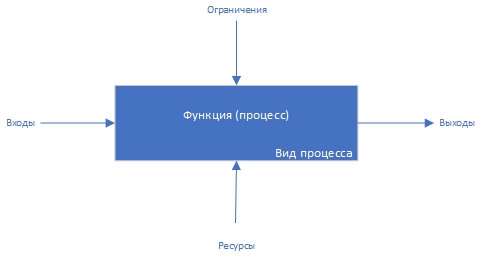 Рис. 1.3 – Элементы схемы нотации IDF0 Исходя из данной нотации нарисуем схему бизнес-процесса управления автосервисом Рис. 1.4 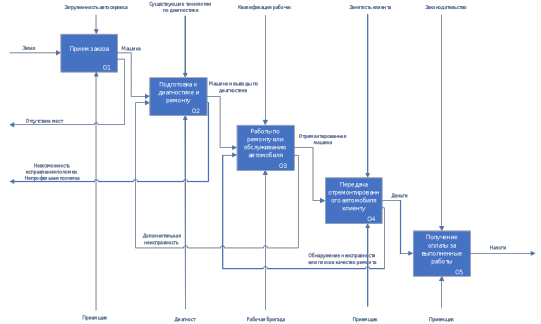 Рис. 1.4 – Модель процессов управления автосервисом (нотация IDF0) |
