Курсовая по диффурам. Задание Для данного дифференциального уравнения методом изоклин построить интегральную кривую, проходящую через точку Решение Построим поле направлений для данного дифференциального уравнения.
 Скачать 1.53 Mb. Скачать 1.53 Mb.
|
|
Задание 1. Для данного дифференциального уравнения методом изоклин построить интегральную кривую, проходящую через точку 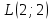 : :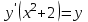 . .Решение: Построим поле направлений для данного дифференциального уравнения. Изоклины, соответствующие направлениям поля с угловым коэффициентом 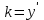 , равны , равны 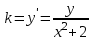 . Отсюда . Отсюда 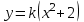 , то есть изоклинами являются параболы. Учтем, что искомая интегральная кривая проходит через точку , то есть изоклинами являются параболы. Учтем, что искомая интегральная кривая проходит через точку 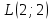 , и сделаем чертеж: , и сделаем чертеж: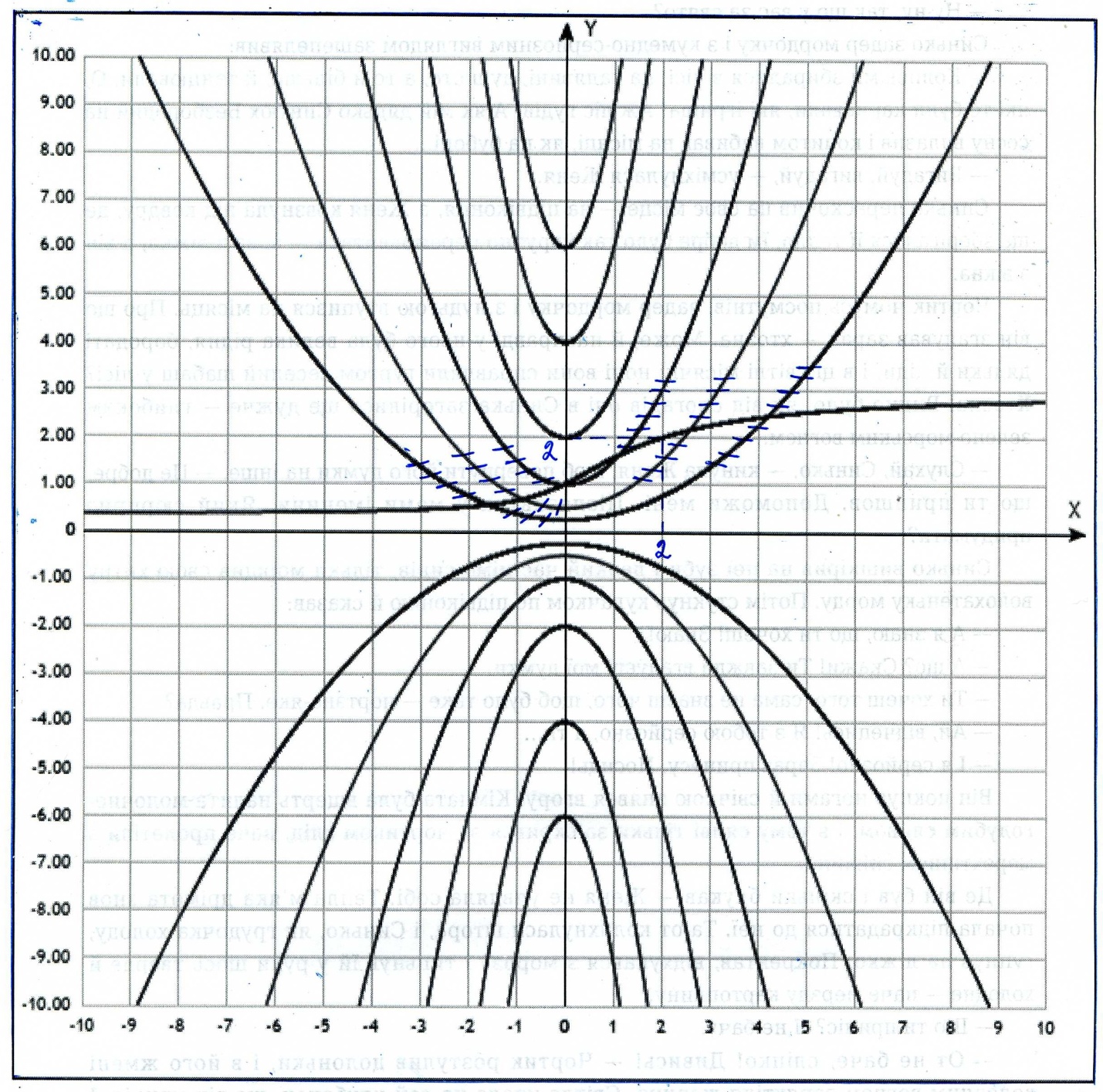 Задание 2. Найти линию, проходящую через 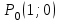 , если отрезок любой ее нормали, заключенный между осями координат, делится точкой линии в отношении , если отрезок любой ее нормали, заключенный между осями координат, делится точкой линии в отношении 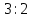 (считая от оси ОY). (считая от оси ОY).Решение: Сделаем чертеж: 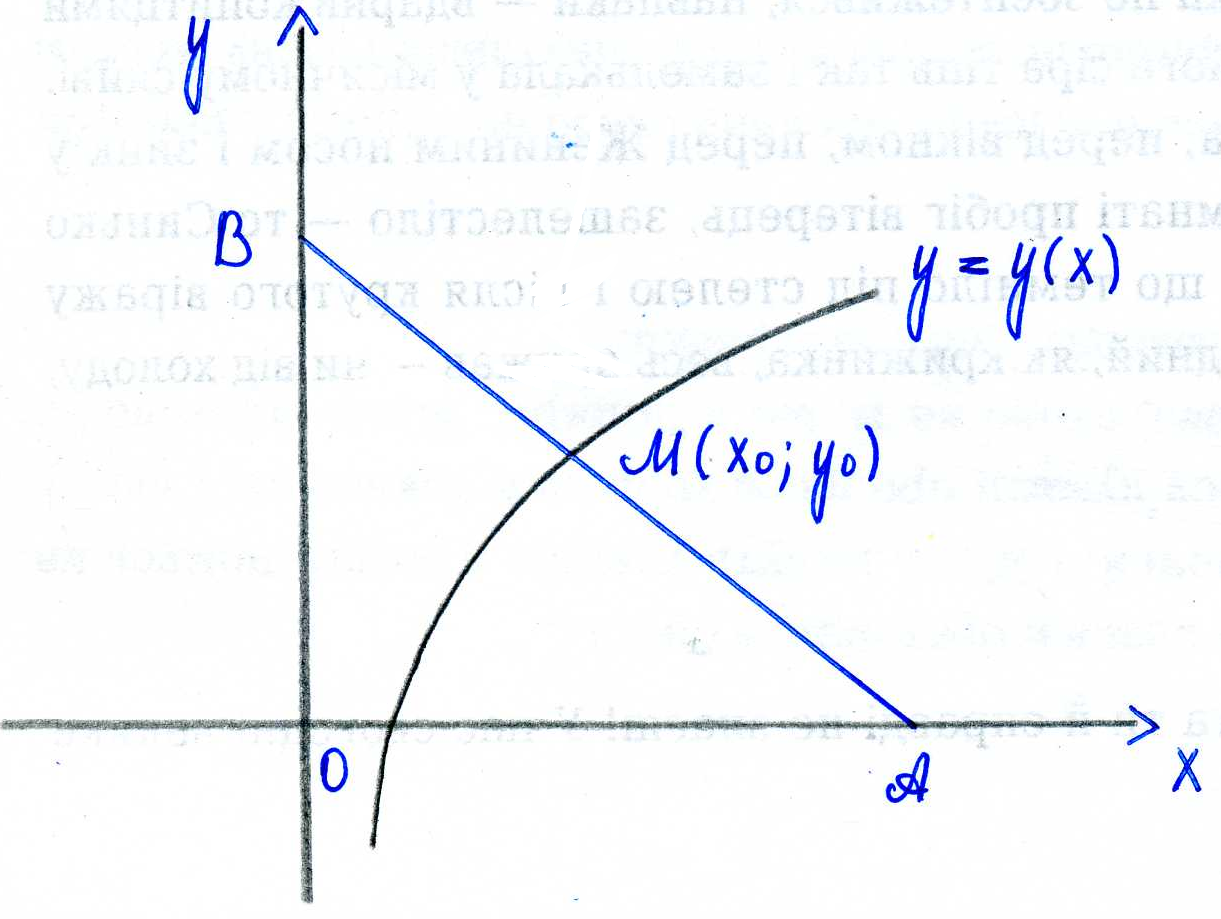 Уравнение нормали к кривой 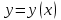 в точке в точке 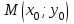 имеет вид имеет вид 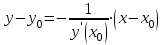 . В точке . В точке 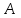 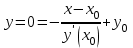 , откуда , откуда 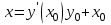 . В точке . В точке 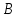 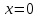 , , 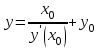 . По условию задачи . По условию задачи 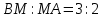 , откуда , откуда 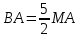 или или 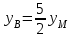 , или , или 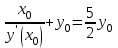 . Опускаем индекс “ноль” и получаем следующее дифференциальное уравнение: . Опускаем индекс “ноль” и получаем следующее дифференциальное уравнение: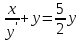 , , 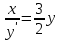 , , 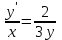 , ,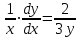 , , 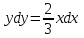 , , 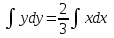 , ,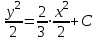 , , 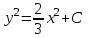 , , 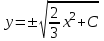 . .Константу 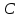 определим из начального условия: определим из начального условия: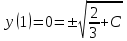 , , 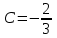 . .Тогда получаем: 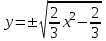 , , 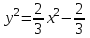 , , 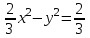 , ,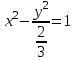 - искомая линия, являющаяся гиперболой. - искомая линия, являющаяся гиперболой.Задание 3. Найти общий интеграл дифференциального уравнения: 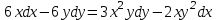 . .Решение: Представим данное уравнение в следующем виде: 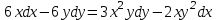 , , 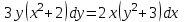 , ,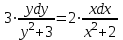 , , 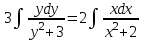 , ,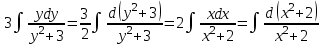 , ,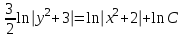 , , 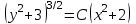 , ,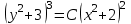 - общий интеграл данного дифференциального уравнения. - общий интеграл данного дифференциального уравнения.Задание 4. Найти общий интеграл дифференциального уравнения: 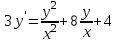 . .Решение: Сделаем замену 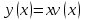 , , 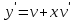 . Тогда получаем: . Тогда получаем: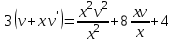 , , 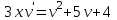 , ,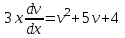 , , 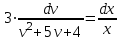 , ,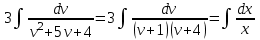 . .Используем метод неопределенных коэффициентов: 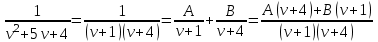 , ,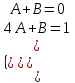 , , 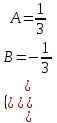 . .Тогда получаем: 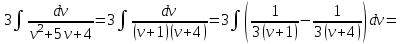 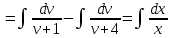 , ,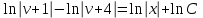 , , 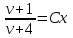 , , 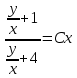 , ,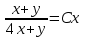 - общий интеграл данного дифференциального уравнения. - общий интеграл данного дифференциального уравнения.Задание 5. Найти общий интеграл дифференциального уравнения: 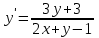 . .Решение: Найдем решение системы уравнений 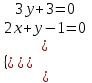 , откуда , откуда 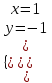 . Сделаем замену . Сделаем замену 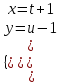 , , 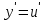 . Тогда получаем: . Тогда получаем: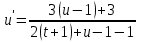 , , 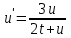 . .Сделаем замену 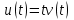 , , 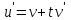 . Тогда получаем: . Тогда получаем: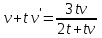 , , 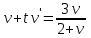 , , 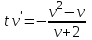 , ,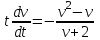 , , 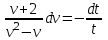 , , 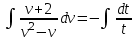 . .Используем метод неопределенных коэффициентов: 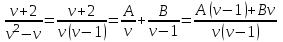 , ,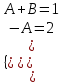 , , 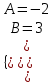 . .Тогда получаем: 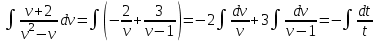 , ,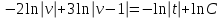 , , 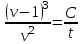 . .Подставляем 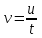 : :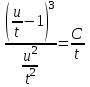 , , 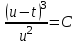 . .Подставляем 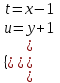 : :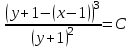 , ,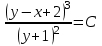 - общий интеграл данного дифференциального уравнения. - общий интеграл данного дифференциального уравнения.Задание 6. Найти общий интеграл дифференциального уравнения: 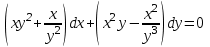 . .Решение: Проверим, является ли данное уравнение уравнением в полных дифференциалах для некоторой функции 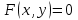 : :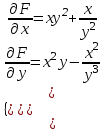 , , 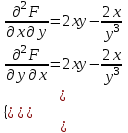 , , 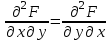 . .Отсюда следует, что данное уравнение является уравнением в полных дифференциалах для некоторой функции 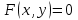 . Тогда получаем: . Тогда получаем: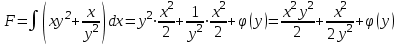 , ,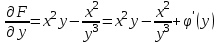 , ,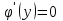 , , 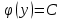 , , 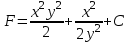 , ,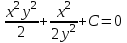 - общий интеграл данного дифференциального уравнения. - общий интеграл данного дифференциального уравнения.Задание 7. Найти решение задачи Коши: 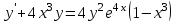 , , 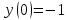 . .Решение: Представим данное уравнение в следующем виде: 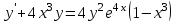 , , 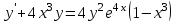 . .Отсюда следует, что 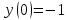 - особое решение данного дифференциального уравнения. Сделаем замену - особое решение данного дифференциального уравнения. Сделаем замену 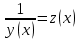 , , 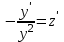 . Тогда получаем: . Тогда получаем: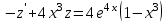 , , 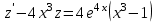 . .Умножим обе части равенства на 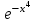 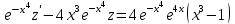 , , 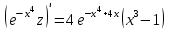 , ,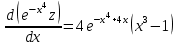 , , 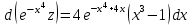 , ,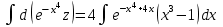 , ,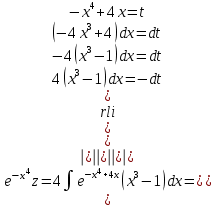 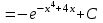 , ,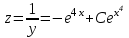 , , 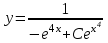 . .Константу 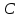 определим из начального условия: определим из начального условия: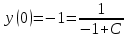 , , 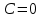 . .Тогда получаем: 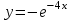 - частное решение данного дифференциального уравнения, удовлетворяющее начальному условию. - частное решение данного дифференциального уравнения, удовлетворяющее начальному условию.Задание 8. Найти решение задачи Коши: 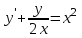 , , 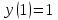 . .Решение: Сделаем замену 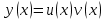 , , 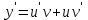 . Тогда получаем: . Тогда получаем: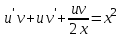 , , 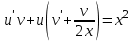 , ,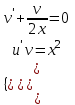 . .Рассмотрим первое уравнение: 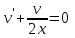 , , 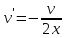 , , 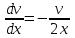 , , 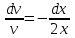 , ,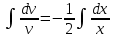 , , 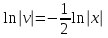 , , 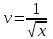 . .Рассмотрим второе уравнение: 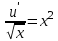 , , 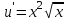 , , 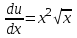 , , 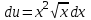 , ,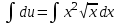 , , 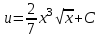 . .Тогда получаем: 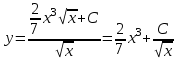 . .Константу 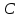 определим из начального условия: определим из начального условия: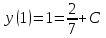 , , 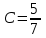 . .Тогда получаем: 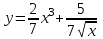 - частное решение данного дифференциального уравнения, удовлетворяющее начальному условию. - частное решение данного дифференциального уравнения, удовлетворяющее начальному условию.Задание 9. Решить задачу Коши: 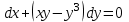 , , 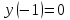 . .Решение: Представим данное уравнение в следующем виде: 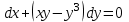 , , 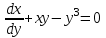 , , 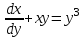 . .Сделаем замену 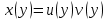 , , 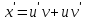 . Тогда получаем: . Тогда получаем: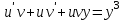 , , 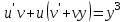 , ,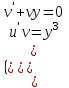 . .Рассмотрим первое уравнение: 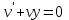 , , 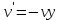 , , 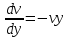 , , 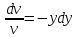 , ,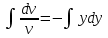 , , 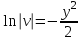 , , 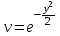 . .Рассмотрим второе уравнение: 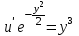 , , 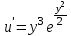 , , 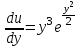 , , 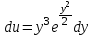 , ,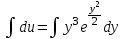 , ,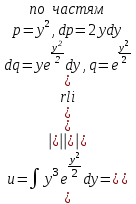 . .Тогда получаем: 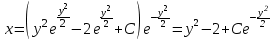 . .Константу 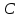 определим из начального условия: определим из начального условия: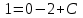 , , 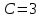 . .Тогда получаем: 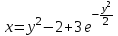 - частный интеграл данного дифференциального уравнения, удовлетворяющий начальному условию. - частный интеграл данного дифференциального уравнения, удовлетворяющий начальному условию.Задание 10. Найти общее решение дифференциального уравнения: 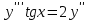 . .Решение: Сделаем замену 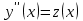 , , 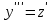 . Тогда получаем: . Тогда получаем: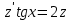 , , 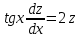 , , 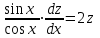 , ,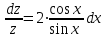 , , 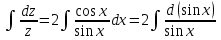 , , , , 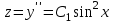 . .Интегрируем обе части полученного уравнения: 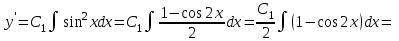 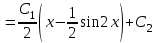 . .Интегрируем обе части полученного уравнения: 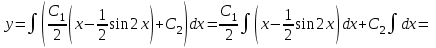 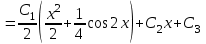 , ,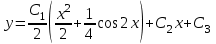 - общее решение данного дифференциального уравнения. - общее решение данного дифференциального уравнения. |
