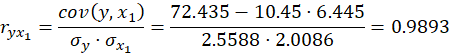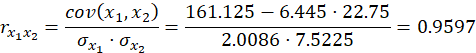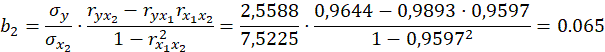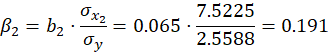Задания множественная регрессия. ЗаданиЕ для выполнения контрольной работы по дисциплине Эконометрика
 Скачать 67.24 Kb. Скачать 67.24 Kb.
|
|
ЗаданиЕ для выполнения контрольной работы по дисциплине «Эконометрика» Исследуется зависимость месячного расхода семьи на продукты питания yi. , тыс.р. от месячного дохода x1i тыс.р. на одного члена семьи (в ценах прошлого века) и от размера семьи x2i, чел. (смотри таблицу своего варианта). Требуется: Построить линейную модель множественной регрессии. Записать стандартизованное уравнение множественной регрессии. На основе стандартизованных коэффициентов регрессии и средних коэффициентов эластичности ранжировать факторы по степени их влияния на результат. Найти коэффициенты парной, частной и множественной корреляции. Проанализировать их. Найти скорректированный коэффициент множественной детерминации. Сравнить его с нескорректированным (общим) коэффициентом детерминации. С помощью 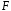 -критерия Фишера оценить статистическую надежность уравнения регрессии и коэффициента детерминации -критерия Фишера оценить статистическую надежность уравнения регрессии и коэффициента детерминации 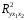 . .С помощью частных 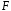 -критериев Фишера оценить целесообразность включения в уравнение множественной регрессии фактора -критериев Фишера оценить целесообразность включения в уравнение множественной регрессии фактора  после после 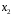 и фактора и фактора 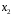 после после  . .Составить уравнение линейной парной регрессии, оставив лишь один значащий фактор.
Для удобства проведения расчетов поместим результаты промежуточных расчетов в таблицу:
Найдем средние квадратические отклонения признаков:   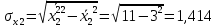 Расчет парных коэффициентов корреляции и параметров линейного уравнения множественной регрессии 1) Для нахождения параметров линейного уравнения множественной регрессии: y=a+b1x1+b2x2 необходимо решить следующую систему линейных уравнений относительно неизвестных параметров : a1,b1,b2: 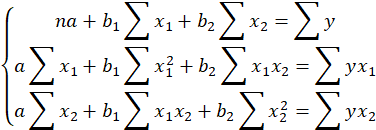 Решать систему уравнений методом Крамера, методом обратной матрицы или методом Гаусса достаточно трудоемко, поэтому воспользуемся готовыми формулами: Рассчитаем сначала парные коэффициенты корреляции:
Находим:
Таким образом, получили следующее уравнение множественной регрессии:  Коэффициенты стандартизированного уравнения регрессии Коэффициенты 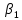 и и 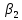 стандартизированного уравнения регрессии стандартизированного уравнения регрессии
То есть уравнение будет выглядеть следующим образом: 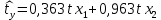 Так как стандартизованные коэффициенты регрессии можно сравнивать между собой, то можно сказать, что размер семьи оказывает большее влияние на месячный расход семьи на продукты питания, чем месячный доход на одного члена семьи. Коэффициенты эластичности Сравнивать влияние факторов на результат можно также при помощи средних коэффициентов эластичности:  Вычисляем: Э1=0,3569*(3,4/2,89)=0,42 Э2=0,7891*(3/2,89)=0,82 Т.е. увеличение только месячного дохода на одного члена семьи (от своего среднего значения) или только размера семьи на 1% увеличивает в среднем месячного расхода семьи на продукты питания на 0,42% или 0,82% соответственно. Таким образом, подтверждается большее влияние на результат фактора фактора x2, нежели x1. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||