Финансовы менеджмент. ФИНАНСОВЫЙ МЕНЕДЖМЕНТ1. Задание Финансовая математика
 Скачать 234 Kb. Скачать 234 Kb.
|
|
Вариант задания 1 Задание 1. Финансовая математика 1.a. Рассчитайте настоящую стоимость S1 тыс. руб., которые потребуются через n1 лет при ставке дисконтирования r1 %. 1.b. Рассчитайте с помощью компаундинга сумму вклада через n2 года при условии, что Вы положили в банк S2 тыс. руб. под r2 % годовых. 1.c. За какую сумму Вы согласитесь продать свой бизнес, который приносит Вам S3 тыс. руб. ежегодно, если известно, что банк принимает бессрочные вклады под r3 % годовых? 1.d. Как оценить сегодня доходы, которые вы будете получать ежегодно в течение n4 лет в сумме S4 тыс. руб. если учетная ставка составляет r4 % годовых?
Решение 1.а. Дисконтированная (настоящая, текущая) стоимость — оценка стоимости (текущий денежный эквивалент) будущего потока платежей исходя из различной стоимости денег, полученных в разные моменты времени (концепция временно́й ценности денег). Формула для расчета дисконтированного денежного потока: 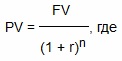 FV—будущая стоимость; PV—текущая стоимость; r—ставка дисконтирования; n — количество лет. PV = 650000/(1 + 0,05)5,5=650000/1,308=496941,90 руб. 1.b. Наращивание (компаундинг) - это процесс увеличения первоначальной суммы денежных средств в результате начисления процентов. Определяется по формуле: S = P(1+i) n где S – наращенная сумма денежных средств; P – первоначальная сумма денежных средств; n – период времени; i – ставка процента. S = 800000* (1+0,11)5=800000* 1,6851= 1348080 руб. 1.с. Стоимость бизнеса определим по формуле: VC = CF/r, где CF - ежегодный доход; r - ставка процента. VC = 160/0,05 = 3200 тыс. руб. Таким образом, продать бизнес целесообразно за 3200 тыс. руб. 1.d. Определим дисконтированную стоимость по формуле: CF - денежный поток; r - ставка процента; n - число лет. Получаем: PV = 80000*(1- (1 + 0,085)-4) = 262023,53 руб. 0,085 Таким образом, дисконтированная стоимость платежей составит 262023,53 руб. Задание 2 «Структура бухгалтерского баланса» 2.a. В составе имущества предприятия внеоборотные активы составляютS1 140 млн. руб., оборотные активы составляют S2 180 млн. руб. Величина собственного капитала составляет S3160 млн. руб. Рассчитайте величину заемного капитала. 2.b. Сумма внеоборотных и оборотных активов предприятия составляет S4 1200 млн. руб. Рассчитайте величину собственного капитала, если доля заемного капитала составляет R % в величине всего капитала предприятия.
Решение 2.a. Под заемным капиталом понимаются все заемные средства (как долгосрочные и краткосрочные займы, так и кредиторская задолженность, то есть текущие обязательства). Из суммы всех активов (т. е. оборотные активы+ внеоборотные активы) вычитаем собственный капитал = заемный капитал. Заемный капитал = (140 млн.руб. + 180 млн. руб.) – 160 млн. руб.= 160 млн. руб. 2.b. Данная задача решается с учетом основных балансовых соотношений: 1) сумма актива (хозяйственных средств предприятия) равна сумме пассива (источников хозяйственных средств), т.е. А=П; 2) актив состоит из внеоборотных (ВА) и оборотных активов (ОА), т.е. А=ВА+ОА; 3) пассив состоит из собственного (СК) и заемного капитала: П=СК+ЗК. ВА+ОА=СК+ЗК ЗК=1 200 млн.руб. *0,2=240 млн.руб. СК= 1 200 млн.руб. – 240 млн.руб. = 960 млн.руб. Задание 3 «Выбор источника финансирования» Предприятие рассматривает вопрос о приобретении оборудования. Первый вариант — лизинг за S1 тыс.руб. с рассрочкой платежа в течение четырех лет. Второй вариант — покупка на заводе-изготовителе за S2 тыс руб. Ставка налога на прибыль равна T %. Предоплата и остаточная стоимость оборудования равны нулю. Можно получить кредит в банке под г% годовых. Используется равномерное начисление износа. Сравнить эти варианты.
Решение 1. В случае лизинга. Ежегодный лизинговый платеж равен: L0= 700 тыс.руб./4 = 175 тыс. руб. / год Тогда чистая приведенная стоимость после налоговых лизинговых платежей L равна: L = E0 + (1 – Kн) × L0 где L – чистая приведенная стоимость посленалоговых платежей; E0 – предоплата; Kн – ставка налога на прибыль; L0 – сумма ежегодных лизинговых платежей; n – срок реализации проекта; r – процентная ставка за кредит; 3,103 Таким образом: L = 0+(1–0,3)×175×1-1/(1+0,11)4 ≈ 380,12 тыс. руб. 0,11 2. В случае кредита. Определим график погашения кредита при покупке оборудования. Заполним таблицу 1. Таблица 1 – Расчет сумм возврата кредита и процентов по нему
Ежегодный возврат кредита: S0= 560 / 4 = 140 тыс. руб./год Каждое число 2-й строки, начиная с 3-го столбца, есть разность предыдущего числа 2-й строки и числа из этого же столбца предыдущей строки. Каждое число 2-й строки умножаем на 0,11 и результат пишем в следующем столбце 3-й строки. Ежегодные амортизационные начисления равны: А0 =(первоначальная стоимость – остаточная стоимость) / количество лет. Таким образом: А0 = (560 – 0) / 4 = 140 тыс. руб./год Тогда чистая приведенная стоимость после налоговых платежей в случае покупки за счет кредита равна: S=E0+(S0–KnA0)× Тогда: S=0+(140–0,3×140)× 1-1/(1+0,11)4 +(1–0,3)×(61,6/(1+0,11)1+ 0,11 + 46,2/1,112 + 30,8/1,113 + 15,4/1,114) – 0 ≈ 392,03 тыс. руб. Так как 380,12 тыс. руб. < 392,03 тыс. руб., то выгоднее лизинг. Задание 4 «Оценка инвестиционного проекта» Предприятие анализирует два инвестиционных проекта в S млн. руб. Оценка чистых денежных поступлений приведена в таблице.
Альтернативные издержки (ставка дисконтирования) по инвестициям равны r %. 4.а. Определить чистую приведенную стоимость каждого проекта. Какой проект предпочтительнее? 4.b. Определить внутреннюю норму доходности каждого инвестиционного проекта. 4.c. Определить период окупаемости каждого инвестиционного проекта.
Решение 4.а. Метод «Чистой приведенной стоимости» (NPV) основан на сопоставлении дисконтированной стоимости денежных поступлений за прогнозируемый период и инвестиций (капиталовложений). 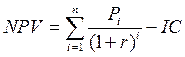 , , где n – расчетный период; Рi – денежные поступления в году i; r – коэффициент дисконтирования. Чистая приведенная стоимость проекта А равна: (1,1/1+0,11) + (1,5/(1+0,11)2) -2,1=0,10 млн.руб. Чистая приведенная стоимость проекта В равна: (0,8/1+0,11) + (1,2/(1+0,11)2) + (1,6/(1+0,11)3) - 2,1=0,75 млн.руб. Так как 0,75 > 0,1, то проект В предпочтительнее. 4.b. Внутренняя норма доходности – коэффициент, показывающий максимально допустимый риск по инвестиционному проекту или минимальный приемлемый уровень доходности. Для определения способа вычисления ВНД используется уравнение: 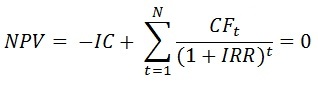 , ,где: NPV — размер ЧПС; IC — начальная сумма инвестиций; CFt — приток денег за временной период; IRR — внутренняя норма доходности. Учитывая это уравнение, определяем показатель IRR по формуле: 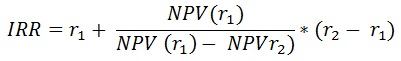 , ,где r — процентная ставка. Расчет ВНД для проекта А. 1) минимальное значение ВНД проекта А:  , , где N — число лет; IC — первоначальная стоимость вклада; ∑ — сумма доходов за каждый год. ²√ 1,1+1,5 -1 =1,1127 – 1=0,11=11% 2,1 2) максимальное значение ВНД проекта А: IRRmax=1,1+1,5/2,1 – 1=0,24=24% ВНД проекта А находится в промежутке от 11 до 24 %. Рассмотрим величину NPV для каждого значения: NPV (11%)= -2,1+1,1/1,11+1,5/1,23=0,11 NPV (24%)= -2,1+1,1/1,24+1,5/1,54=-0,24 Теперь рассчитаем IRR для проекта А: IRR=0,11+0,11/0,11- (-0,24)*(-0,24-0,11)=0% Расчет ВНД для проекта В. 1) минимальное значение ВНД проекта В: 3√ 0,8+1,2+1,6 -1 =1,20 – 1=0,20=20% 2,1 2) максимальное значение ВНД проекта В: IRRmax=0,8+1,2+1,6/2,1 – 1=71% ВНД проекта В находится в промежутке от 20 до 71 %. Рассмотрим величину NPV для каждого значения: NPV (20%)= -2,1+0,8/1,20+1,2/1,44+1,6/1,73=0,32 NPV (71%)= -2,1+0,8/1,71+1,2/2,92+1,6/5,00=-0,90 Теперь рассчитаем IRR для проекта В: IRR=0,20+0,32/0,32- (-0,90)*(-0,90-0,32)=12% Принятие решения по инвестиционному проекту по критерию IRR основывается на правиле: если значение IRR больше ставки финансирования проекта, то данный проект следует принять, и наоборот. Так как IRR>r 12%>11%, то принимаем проект В. 4.c. Дисконтированный срок окупаемости проекта – это временной период, в течение которого полученная прибыль перекроет объем использованных инвестиций. При этом и сумма прибыли, и объем вложенных средств рассчитываются с учетом барьерной ставки или ставки дисконтирования. 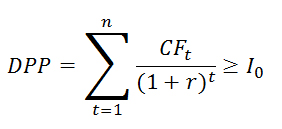 где: DPP – дисконтированный период окупаемости проекта; CF – денежный поток за определенный период времени; I0 – вложения на начальном этапе; n – количество временных периодов (в годах); t – порядковый номер временного периода; r – ставка дисконтирования. Срок окупаемости проекта А: DPP= 1,1/(1+0,11)1 +1,5/(1+0,11)2 =0,99+1,22=2,2 года Срок окупаемости проекта В: DPP= 0,8/(1+0,11)1 +1,2/(1+0,11)2 +1,6/(1+0,11)3 =0,72+0,97+1,17=2,9 года Таким образом, вложения на начальном этапе окупятся быстрее по проекту А. Но при выборе наиболее привлекательного проекта необходимо учитывать и другие показатели: NPV, IRR. |
