Задание на расчетно-графическую работу. КР4_046. Задание на расчетнографическую работу
 Скачать 0.52 Mb. Скачать 0.52 Mb.
|
|
Задание на расчетно-графическую работу Разветвленная магнитная цепи (рис. 1) представляет собой трехстержневой сердечник из листов электротехнической стали, кривая намагничивания которой представлена в табл. 1. Для этой цепи надо выполнить следующее: 1. Начертить эквивалентную схему магнитной цепи, указав на ней направление магнитных потоков и магнитодвижущих сил (МДС). 2. Составить систему уравнений по законам Кирхгофа для магнитной цепи. 3. Определить магнитные потоки в стержнях, магнитное напряжение и значение магнитной индукции в воздушном зазоре. Размеры магнитной цепи на рис. 1 указаны в мм. В табл. 2 даны величины токов и число витков обмотки для каждого варианта. Примечание. При расчете цепи потоками рассеяния пренебречь. Таблица 1 Кривая намагничивания
Таблица 2 Числовые значения параметров цепи
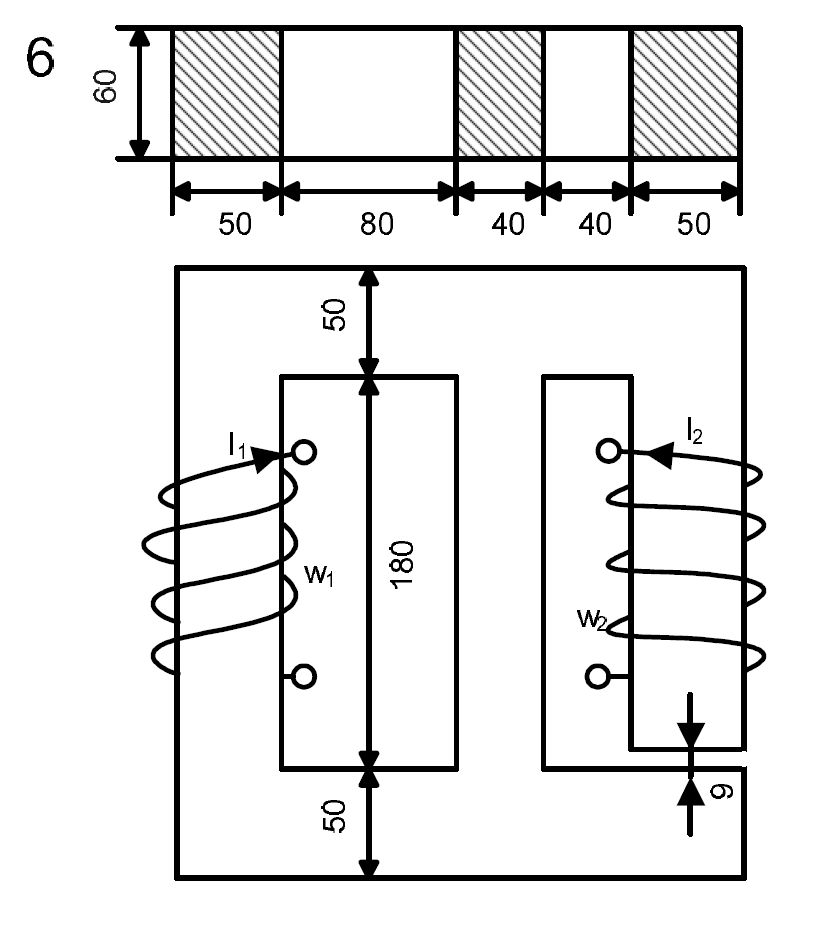 Рис. 1. Магнитная цепь Расчет разветвленной магнитной цепи постоянного тока 1. Составление эквивалентной схемы Данная магнитная цепь имеет два узла, обозначим их на эквивалентной схеме как а и b, три ветви, один воздушный зазор и два источника МДС, направление которых определяем по правилу правой руки. Первая МДС направлена вверх, вторая – вниз. Эквивалентная схема будет представлять собой три параллельно соединенные ветви (рис. 2). Первая ветвь состоит из последовательно соединенных источника МДС На эквивалентной схеме показываем направления магнитных потоков: магнитные потоки 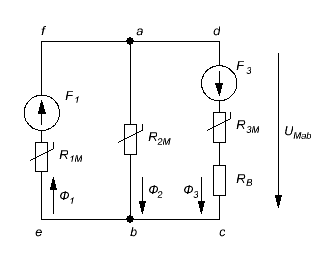 Рис. 2. Эквивалентная схема магнитной цепи 2. Законы Кирхгофа для магнитной цепи Для расчета электрической цепи непосредственно по законах Кирхгофа надо составить по первому закону Кирхгофа на одно уравнение меньше, чем количество узлов, а по второму – количество ветвей минус количество уравнений, составленных по первому закону. Поскольку цепь содержит два узла и три ветви, по первому закону надо составить одно уравнение, по второму – два. Составляем уравнения. Примем, что втекающие магнитные потоки будут записаны со знаком плюс, а вытекающие – с минусом. Тогда для узла а по первому закону Кирхгофа для магнитной цепи получаем: Запишем уравнения по второму закону Кирхгофа для контуров abefaиadcba. Выбираем направление обхода обоих контуров по часовой стрелке. abefa: adcb: Полученная система уравнений будет выглядеть следующим образом: 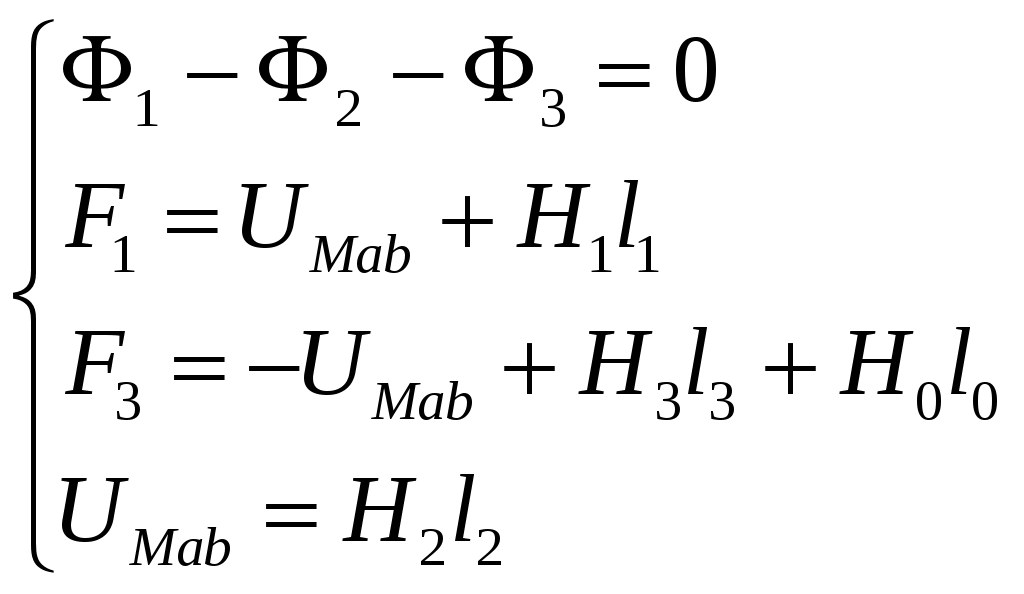 3. Решение нелинейной системы уравнений Полученная система нелинейных уравнений может решена графоаналитическим методом. Для этого необходимо построить зависимости магнитных потоков от магнитного напряжения Прежде чем строить необходимые зависимости, выполним следующее. 1. Определим площади поперечного сечения участков магнитопровода 2. Определяем длины участков средней линии 3. Вычисляем: 3.1. Магнитодвижущие силы: 3.2. Напряженность поля в воздушном зазоре 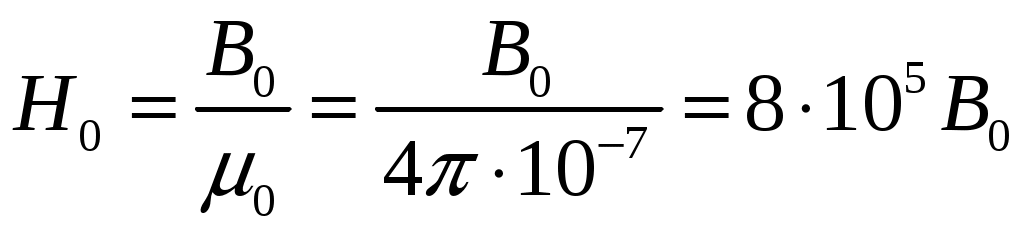 , А/м. , А/м.3.3. Произведение 4. По табличным данным (табл. 1) строим кривую намагничивания (рис. 3). 5. Из уравнений, составленных по второму закону Кирхгофа для магнитных цепей 6. Вычисляем для заданных значений потоков 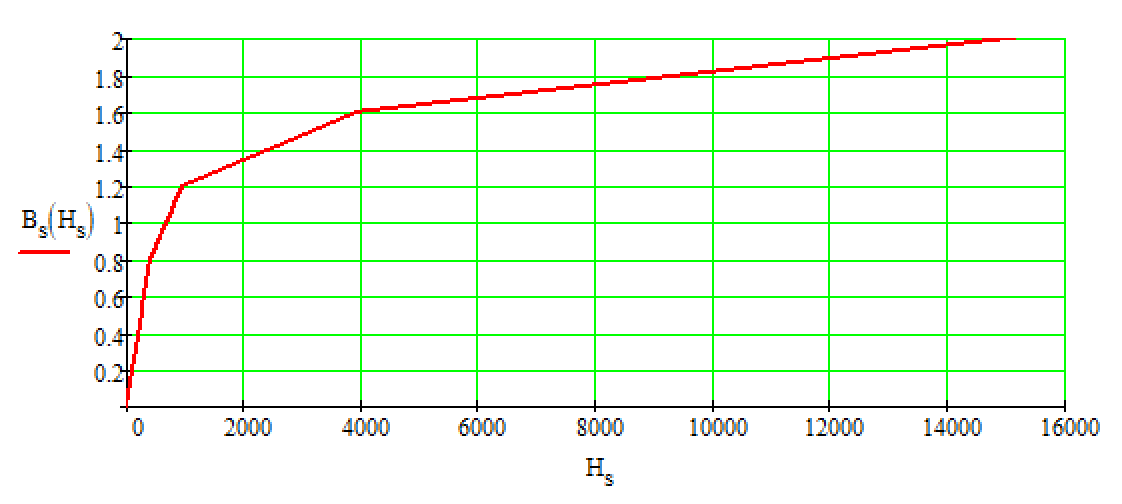 Рис. 3. Кривая намагничивания Далее для каждого заданного значения В по кривой намагничивания (рис. 3) определим напряженность магнитного поля магнитопровода Н. По известным значениям напряженности магнитного поля Н вычислим магнитное напряжение Например, при магнитной индукции Вычислим магнитные потоки: Магнитное напряжение на участках магнитопровода для различных участков определяем как: Результаты вычислений представлены в табл. 3-5. Таблица 3 Расчетные данные для построения зависимости
Таблица 4 Расчетные данные для построения зависимости
Таблица 5 Расчетные данные для построения зависимости
На основании результатов вычислений, представленных в табл. 3-5, строим зависимости а 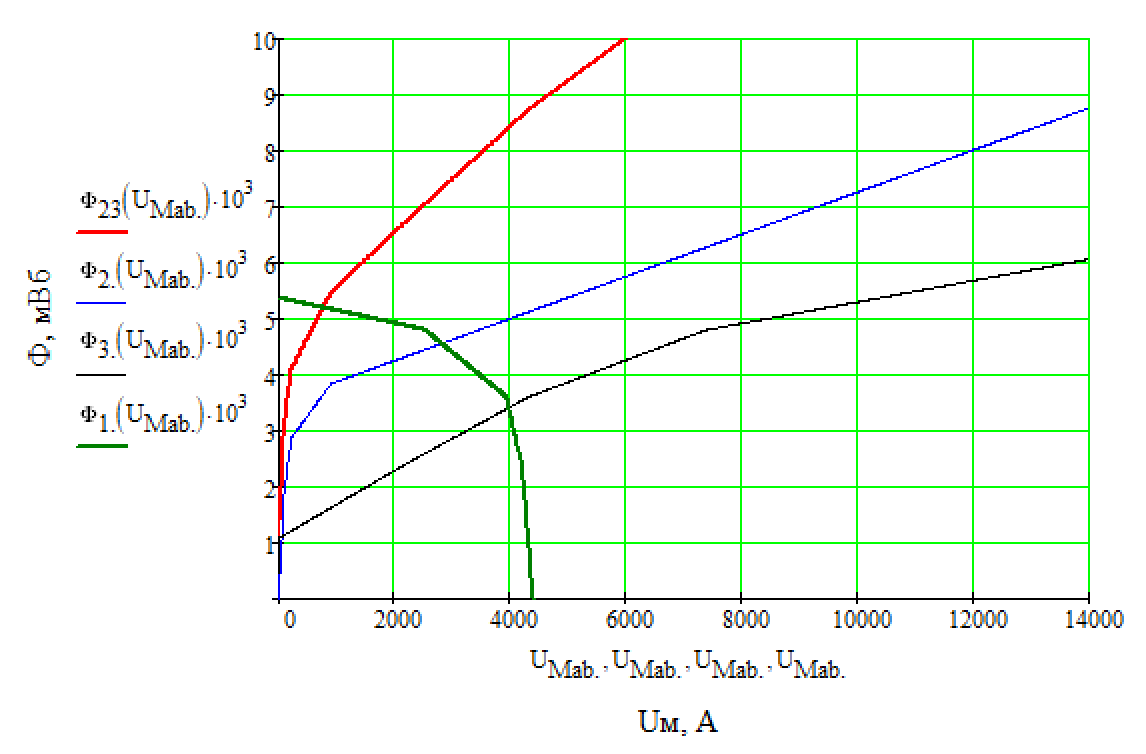 б 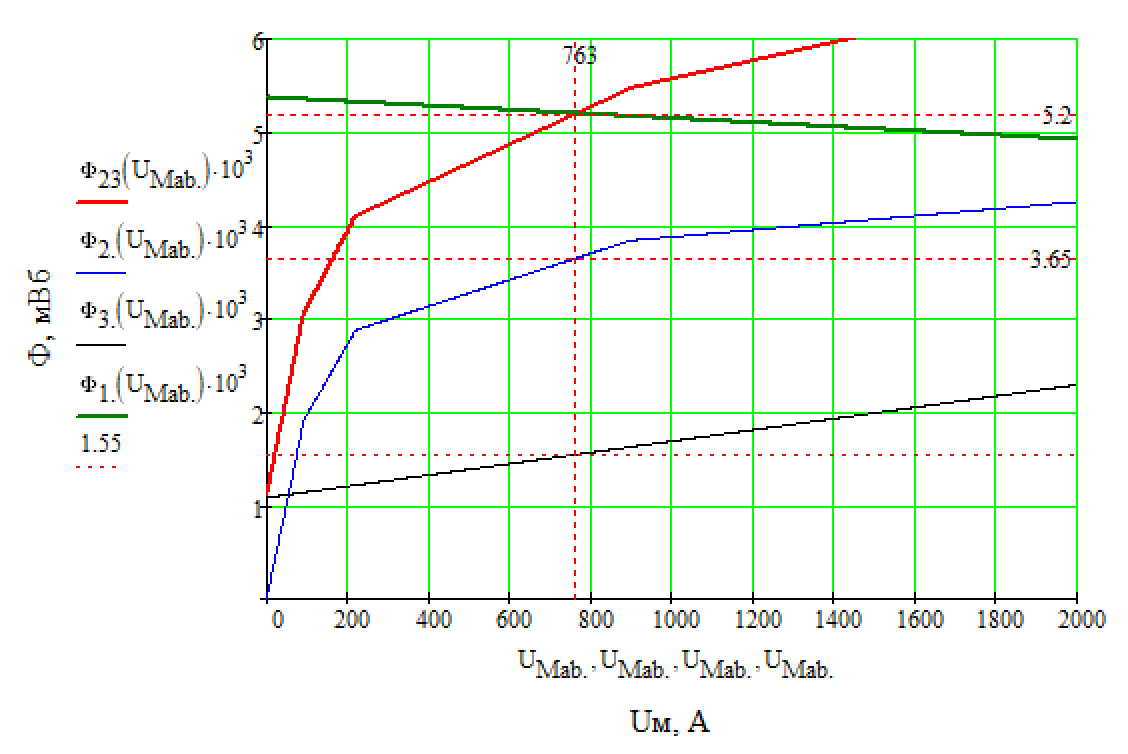 Рис. 4. Зависимости Последнюю кривую строим, суммируя ординаты кривых Из рис. 4 видно, что кривые Проведем прямую, параллельную оси ординат. Точки пересечения проведенной прямой с кривыми Определим значения магнитной индукции и магнитного напряжения в воздушном зазоре. Пренебрегая магнитными потоками рассеяния будем считать, что 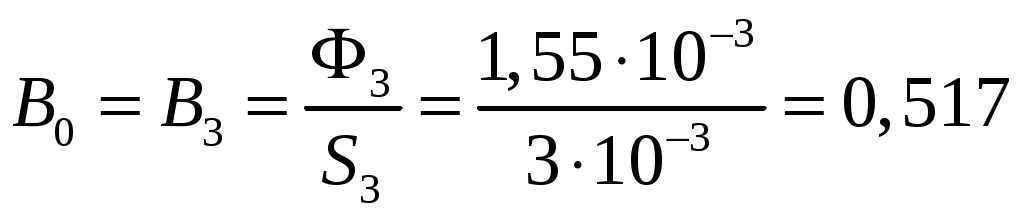 Тл, Тл, |
