Курсовик. Задание на расчетнографическую работу
 Скачать 178.05 Kb. Скачать 178.05 Kb.
|
|
Задание на расчетно-графическую работу Задание 11 вариант Г
1.Структурный анализ механизма Вычерчивается структурная схема механизма 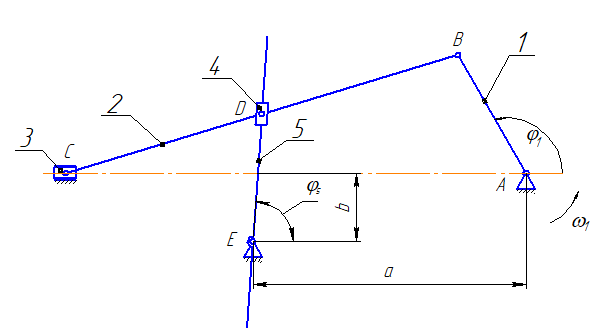 Рисунок 1.1 – Схема исследуемого механизма Данный механизм служит для преобразования вращательного движения кривошипа 1 в поступательное движение ползуна 3. Таблица 1 – Звенья механизма.
Таблица 2 – Кинематические пары.
Число одноподвижных кинематических пар Р5=7, число двухподвижных кинематических пар Р4=0. Определяется степень подвижности механизма по формуле Чебышева: W = 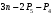 , (1.1) , (1.1)где: n – число подвижных звеньев; 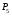 – число кинематических пар пятого класса; – число кинематических пар пятого класса;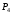 – число кинематических пар четвертого класса. – число кинематических пар четвертого класса.W= 35 - 27 – 0 =1. При W=1 в схеме механизма одно ведущее звено. Это звено – АВ. Определяется класс механизма. Для этого механизм разбивается на группы Ассура и его класс определяется по классификации Ассура- Артоболевского (см. таблицу 3). Таблица 3 – Классификация структурных групп
Записывается формула строения механизма: 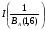 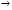 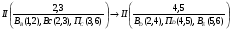 Класс всего механизма II, т.к наивысший класс группы Ассура, входящей в данный механизм – II. 2.Кинематический анализ механизма Выбирается масштаб длин для построения схемы механизма: 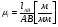 , (1.2) , (1.2)где lAB– истинная длина; AB – выбранный чертёжный размер. Звено АВ на схеме выбирается произвольно. Приняв на чертеже отрезок AB=50 мм, находим: 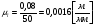 Определяем длины звеньев на схеме: 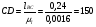 мм мм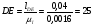 мм мм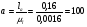 мм ммВ масштабе µ=0,0016 м/мм вычерчивается схема. Для построения 12 положений звеньев механизма разделим траекторию, описываемую точкой B кривошипа AB, на 12 равных частей. По данной схеме определяется положение выходного угла 1. За нулевую точку принимаем точку пересечения оси перемещения ползуна 3 с осью вращения кулисы 5. Значения 5 приведены в таблице 4. Таблица 4 – Перемещение выходного угла
Для построения графика перемещения выходного звена задаём масштабы: - масштаб угла поворота μφ1 = 360 / 180 = 2 град./мм, - масштаб перемещения μφ5 = 1 град/мм, т.е. одному миллиметру ординаты графика соответствует перемещение 1 град. По данным таб.4, в заданном масштабе строим график зависимости 5(1). По графику перемещения методом графического дифференцирования (метод касательных) построим график зависимости приведённой скорости 5от угла 1. Для этого разбиваем абсциссу на равное число отрезков и проводим в этих точках ординаты. В точках пересечения ординат с графиком 5(1)проводим касательные. Строим систему координат 5(1). Масштаб угла поворота принимаем такой же как на графике 5(1). μφ1 = 2 град./мм. На продолжении абсциссы отмечаем полюс Н. Полюсное расстояние ОН выбираем произвольно, ОН = 22,5 мм. Из полюса проводим прямые параллельные касательным графика 5(1) Из точек пересечения касательных с осью 5 проводим горизонтальные прямые и находим точки пересечения их с соответствующими ординатами из точек на оси 1. Соединив полученные точки пересечения плавной кривой, находим график приведённой скорости 5(1). Масштаб скорости находим по формуле: 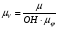 (1.3) (1.3)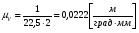 3.Построение планов скоростей Определяем скорость точки B кривошипа по формуле: 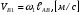 (1) (1)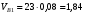 м/с м/сНазначаем полюс плана скоростей РV и из него перпендикулярно кривошипу АВ, в направлении вращения кривошипа строим вектор VBМасштабный коэффициент принимаем: 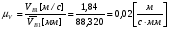 Вектор скорости точки 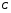 находим как векторную сумму скорости точки B и относительной скорости находим как векторную сумму скорости точки B и относительной скорости 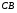 относительно точки относительно точки 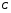 : :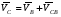 (2) (2)Вектор VСBнаправлен перпендикулярно звену BC. Вектор точки C направлен горизонтально (параллельно оси перемещения ползуна 3). Таким образом проводим из полюса плана скоростей горизонтальную прямую, а из конца вектора VВ прямую перпендикулярную звену ВС. На пересечении этих прямых находится конец вектора скорости точки C. Вектор скорости точки D5 находим как векторную сумму скорости точки 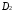 и относительной скорости точки D5 относительно точки C: и относительной скорости точки D5 относительно точки C: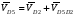 (3) (3)Вектор находим VD2 по 3 свойству планов скоростей. Конец вектора VD2 лежит на середине вектора 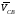 . . Вектор VD5D2 направлен параллельно звену ED. ВекторVD5 перпендикулярен звену ED. Таким образом проводим из конца вектора VD2 линию параллельную ED, а из полюса плана скоростей линию перпендикулярнуюED. На пересечении этих прямых находится конец вектора скорости точки D5. Строим планы скоростей для 12 положений механизма. Полученные значения приведены в таблице 5. Таблица 5 – скорость выходного звена, полученная методом планов скоростей.
5.Построение плана ускорений. План ускорений строим для положения механизма при 1=30. Определяем ускорение точки 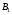 кривошипа по формуле кривошипа по формуле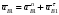 (4) (4)где: 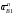 – нормальное ускорение точки – нормальное ускорение точки 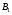 . .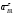 – тангенциальное ускорение точки – тангенциальное ускорение точки 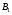 . .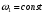 , поэтому , поэтому 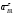 =0. =0.Нормальное ускорение определяется выражением: 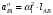 (5) (5)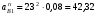 м/с2 м/с2Этот вектор направлен параллельно АВ от точки 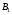 к центру вращения кривошипа. к центру вращения кривошипа.Назначаем полюс плана ускорений Рa и из него параллельно звену АВ от точки 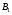 к центру вращения кривошипа строим вектор к центру вращения кривошипа строим вектор 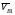 . Масштабный коэффициент принимаем: . Масштабный коэффициент принимаем: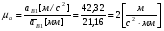 Ускорение точки 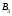 находим по формуле: находим по формуле: 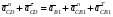 (6) (6)где: 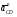 – нормальная составляющая относительного ускорения точки – нормальная составляющая относительного ускорения точки 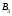 относительно точки С, направлена параллельно BC. относительно точки С, направлена параллельно BC. 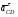 – тангенциальная составляющая относительного ускорения точки – тангенциальная составляющая относительного ускорения точки 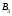 относительно точки С, направлена перпендикулярно ВС. относительно точки С, направлена перпендикулярно ВС.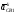 - ускорение Кориолиса точки - ускорение Кориолиса точки 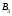 относительно точки относительно точки 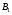 , направлено перпендикулярно BC. , направлено перпендикулярно BC.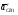 - релятивное ускорение точки - релятивное ускорение точки 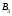 относительно точки относительно точки 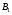 , направлено параллельно BC. , направлено параллельно BC.Нормальная составляющая вычисляется по формуле: 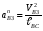 (7) (7)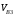 – относительная скорость точки – относительная скорость точки 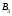 относительно точки С, была найдена нами при построении планов скоростей относительно точки С, была найдена нами при построении планов скоростей 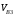 =1,84 м/с. =1,84 м/с.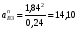 м/с2 м/с2На чертеже вектор 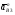 равен: равен: 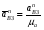 (8) (8)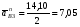 мм ммУгловую скорость найдем по формуле: 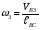 (9) (9)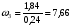 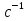 Ускорение Кориолиса вычисляется по формуле: 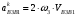 (10) (10)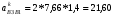 м/с2 м/с2На чертеже вектор 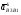 равен: равен: 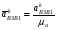 (11) (11)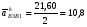 мм ммИз полюса строим вектор 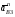 параллельно BC, а из конца параллельно BC, а из конца 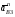 проводим прямую перпендикулярную BC. Из конца вектора проводим прямую перпендикулярную BC. Из конца вектора 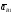 строим вектор строим вектор 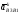 перпендикулярно BC, направленный в противоположную сторону вращения 2 звена. Из конца перпендикулярно BC, направленный в противоположную сторону вращения 2 звена. Из конца 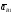 строим прямую параллельную BC. На пересечении этих прямых находится конец вектора ускорения точки строим прямую параллельную BC. На пересечении этих прямых находится конец вектора ускорения точки 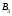 . .Ускорение точки D находим по 3 свойству планов ускорений. Вектор 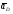 направлен перпендикулярно вектору направлен перпендикулярно вектору 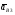 и величина находится из пропорции: и величина находится из пропорции: 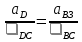 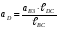 (12) (12)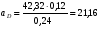 м/с2 м/с2На чертеже вектор 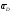 равен: равен: 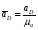 (13) (13)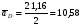 мм ммИз полюса строим вектор 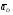 перпендикулярно вектору перпендикулярно вектору 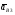 . .Ускорение точки E находим по формуле: 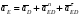 (14) (14)Нормальная составляющая вычисляется по формуле: 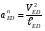 (15) (15)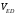 – относительная скорость точки E относительно точки D, была найдена нами при построении планов скоростей VED=0,83465 м/с. – относительная скорость точки E относительно точки D, была найдена нами при построении планов скоростей VED=0,83465 м/с.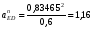 м/с2 м/с2На чертеже вектор 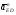 равен: равен: 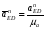 (16) (16)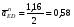 мм ммВектор 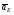 направлен вдоль оси перемещения ползуна, т.е. расположен на горизонтальной прямой. Вектор направлен вдоль оси перемещения ползуна, т.е. расположен на горизонтальной прямой. Вектор 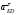 направлен перпендикулярно звену ED. Вектор направлен перпендикулярно звену ED. Вектор 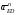 направлен параллельно звену ED от точки D к точке E. направлен параллельно звену ED от точки D к точке E.Таким образом строим из конца вектора 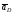 вектор вектор 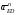 , а из конца вектора , а из конца вектора 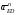 проводим прямую перпендикулярную звену ED. Из полюса плана ускорений проводим прямую параллельную оси перемещения ползуна. На пересечении этих прямых находится конец вектора ускорения точки E. проводим прямую перпендикулярную звену ED. Из полюса плана ускорений проводим прямую параллельную оси перемещения ползуна. На пересечении этих прямых находится конец вектора ускорения точки E. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||