Определение границ и отделение корней. Задание Определение границ и отделение корней. Постановка задачи
 Скачать 0.79 Mb. Скачать 0.79 Mb.
|
|
Задание: Определение границ и отделение корней. Постановка задачи: Определение границ, где находятся корни. Отделение корней, нахождение промежутков, где только один корень. Написание программы для отделения корней. Номер 1: Определить границы следующего уравнения: 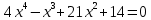 Это алгебраическое уравнение вида: 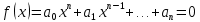 . Из условия видно, что . Из условия видно, что 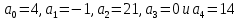 . Найдем область, в которой расположены все корни уравнения. Для этого введем обозначения: . Найдем область, в которой расположены все корни уравнения. Для этого введем обозначения: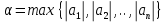 и и 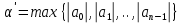 . Сразу запишем численные значения . Сразу запишем численные значения 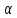 и и 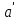 : : 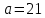 и и 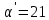 . . Воспользуемся теоремой, которая утверждает, что область, где находятся все корни алгебраического уравнения вида 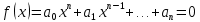 могут быть найдены с помощью неравенства: могут быть найдены с помощью неравенства: 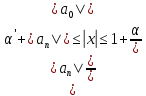 Подставляем значения и получаем: 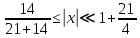 , и как следует получаем следующие границы: , и как следует получаем следующие границы: 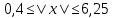 . .Мы определили границы данного в условии уравнения, то есть, нашли область, в которой содержатся все корни уравнения 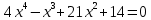 , и границы получились : , и границы получились : 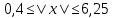 . . Данный номер решен. Подзадание номера 1: Отделить корни уравнения: 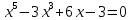 Отделить корни уравнения значит, что нужно найти промежутки, где находится один и только один корень. Как и в первом номере, сначала найдем область, где находятся все корни уравнения. Уравнение в данном номере имеет алгебраический вид 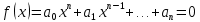 , где , где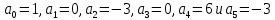 . Вводим обозначения . Вводим обозначения 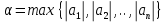 и и 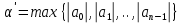 , в данном уравнение их значения будут следующими: , в данном уравнение их значения будут следующими: 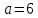 и и 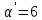 . Следовательно, по уже известному нам неравенству для поиска границ, получаем: . Следовательно, по уже известному нам неравенству для поиска границ, получаем: 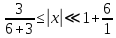 , следовательно: , следовательно: 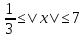 . . Существует теорема, что если непрерывная функция принимает значения разных знаков на промежутке, то внутри такого промежутка существует хотя бы один корень уравнения. Сначала проверим значения на концах промежутка 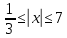 : : 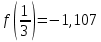 и и 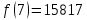 , как видим значения функции имеют разные знаки на концах найденного нами промежутка, следовательно, существует хотя бы один корень. , как видим значения функции имеют разные знаки на концах найденного нами промежутка, следовательно, существует хотя бы один корень. Для отделения корней необходимо воспользоваться производной – если производная существует и сохраняет постоянный знак, значит корень будет единственным. Производная уравнения равна 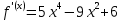 . Ее значения на концах промежутка: . Ее значения на концах промежутка: 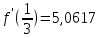 и и 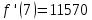 , следовательно функция монотонна возрастает или убывает на этом промежутке и имеет один-единственный корень уравнения в области, которую мы нашли ранее. , следовательно функция монотонна возрастает или убывает на этом промежутке и имеет один-единственный корень уравнения в области, которую мы нашли ранее. Номер 2: Отделить графически корни уравнения 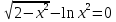 . . Удобнее это уравнение переписать в 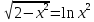 . Таким образом получаем две функции, графики которых нам надо построить: . Таким образом получаем две функции, графики которых нам надо построить: 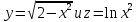 . Корнем исходного уравнения . Корнем исходного уравнения 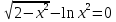 будут считаться точки их пересечения. будут считаться точки их пересечения. График получился следующим: К 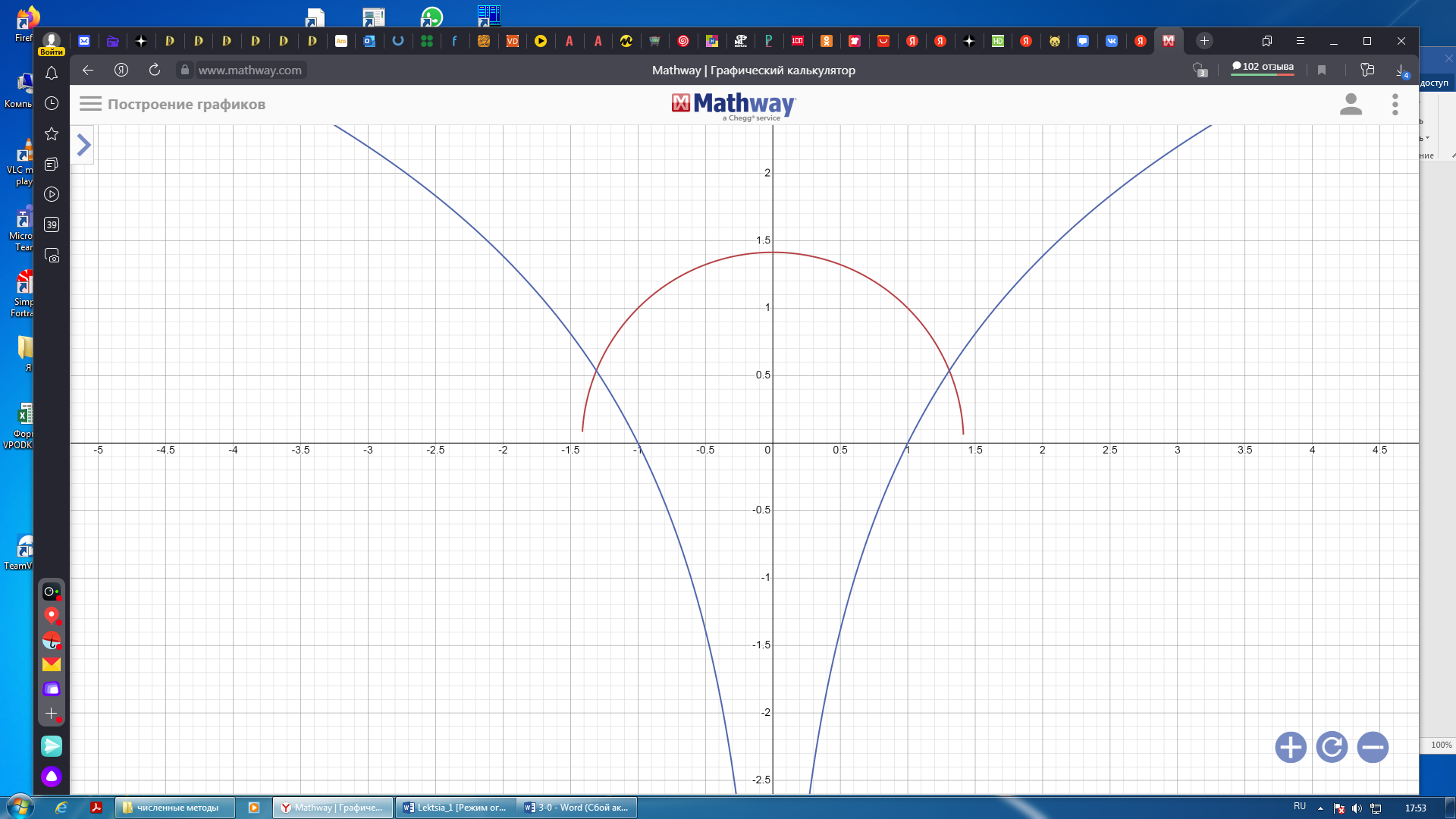 расным: расным: 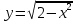 Синим: 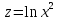 Точек пересечения по графику мы видим две: 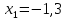 и и 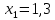 . . Подзадание номера 2: Отделение корней уравнения с помощью компьютера. 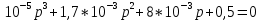 Составим математическую модель, заранее упростим выражение, умножив данное уравнение на 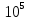 , получаем , получаем 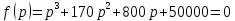 . Уравнение является уравнением третьего порядка, следовательно, будет иметь три корня с учетом их порядка кратности и эти корни могут быть как вещественными, так и комплексными. . Уравнение является уравнением третьего порядка, следовательно, будет иметь три корня с учетом их порядка кратности и эти корни могут быть как вещественными, так и комплексными. Отделить корень, значит найти промежутки, в каждом из которых находится один корень. Чтобы отделить корни данного уравнения (т.е. уравнений третьего порядка), нужно найти производную и решить, полученное выражение: 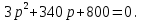 Это квадратное уравнение. Чтобы решить такое уравнение найдем дискриминант и по формуле посчитаем p1, p2: Это квадратное уравнение. Чтобы решить такое уравнение найдем дискриминант и по формуле посчитаем p1, p2: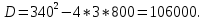 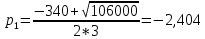 . .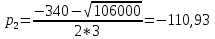 . .Для того чтобы отделить все вещественные корни уравнения, достаточно сначала найти все интервалы монотонности функции, а затем из выбранных интервалов оставить те, на границах которых принимает значения разных знаков. Данная функция монотонна на интервалах 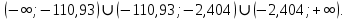 При этом При этом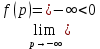 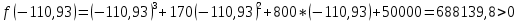 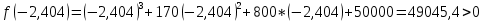 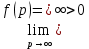 Интервалы монотонности 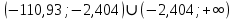 не содержат корней данного уравнения, так как функция не меняет знак на концах. Единственный вещественный корень уравнения расположен между не содержат корней данного уравнения, так как функция не меняет знак на концах. Единственный вещественный корень уравнения расположен между 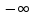 и -110,93. и -110,93.Проанализировав математическую модель, приступим к написанию программы. Сделаем программу, которая подходит не только для данного случая, но и для уравнений третьего порядка. Поэтому для удобства введем функцию общего вида для уравнений третьего порядка, которых имеют вид: 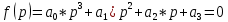 . (см. 70 – 75 строчки программы). Для решения понадобится ввести только коэффициенты a0, a1, a2, a3. (см. 6-8 строчки программы). Так же нужны будут вспомогательные переменные: b0, b1, b2 – коэффициенты после взятии производной; d – дискриминант функции, от которой взята производная; p11, p12 – сортировочные переменные, т.е. переменные нужные только для сортировки корней уравнения, p1, p2 – корни уравнения, полученного из взятия производной функции и приравниванию к нулю выражения; z1, z2- значения функции в найденных корнях. (см. 4 строчку программы). . (см. 70 – 75 строчки программы). Для решения понадобится ввести только коэффициенты a0, a1, a2, a3. (см. 6-8 строчки программы). Так же нужны будут вспомогательные переменные: b0, b1, b2 – коэффициенты после взятии производной; d – дискриминант функции, от которой взята производная; p11, p12 – сортировочные переменные, т.е. переменные нужные только для сортировки корней уравнения, p1, p2 – корни уравнения, полученного из взятия производной функции и приравниванию к нулю выражения; z1, z2- значения функции в найденных корнях. (см. 4 строчку программы).В программе рассматриваются случаи, когда: 1)дискриминант меньше 0 и выдает, что нет вещественных корней; 2) Дискриминант равен нулю и выдает, что существует единственный вещественный корень, который лежит в полученном отрезке; 3) Дискриминант больше нуля и выдает различные случая, исходя из заданного условия. (См. 17-62 строчки программы). В третьем пункте так же происходит сортировка корней по промежутку (см. 34- 40 строчки программы). Программа: 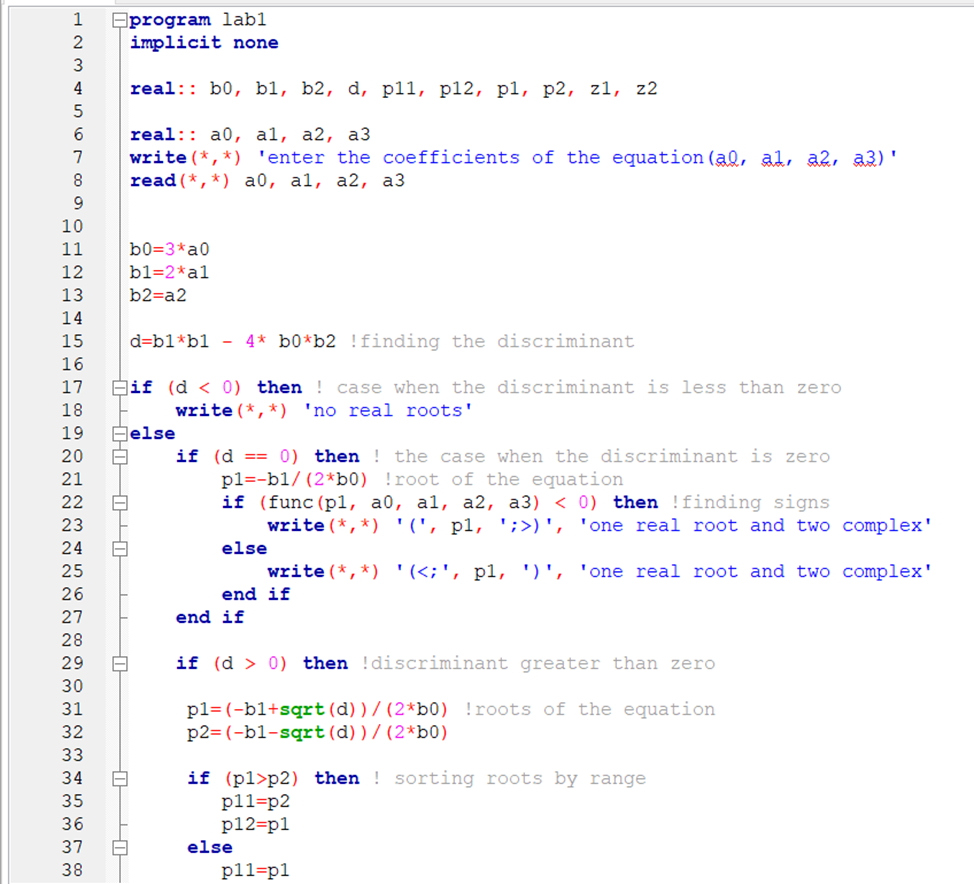 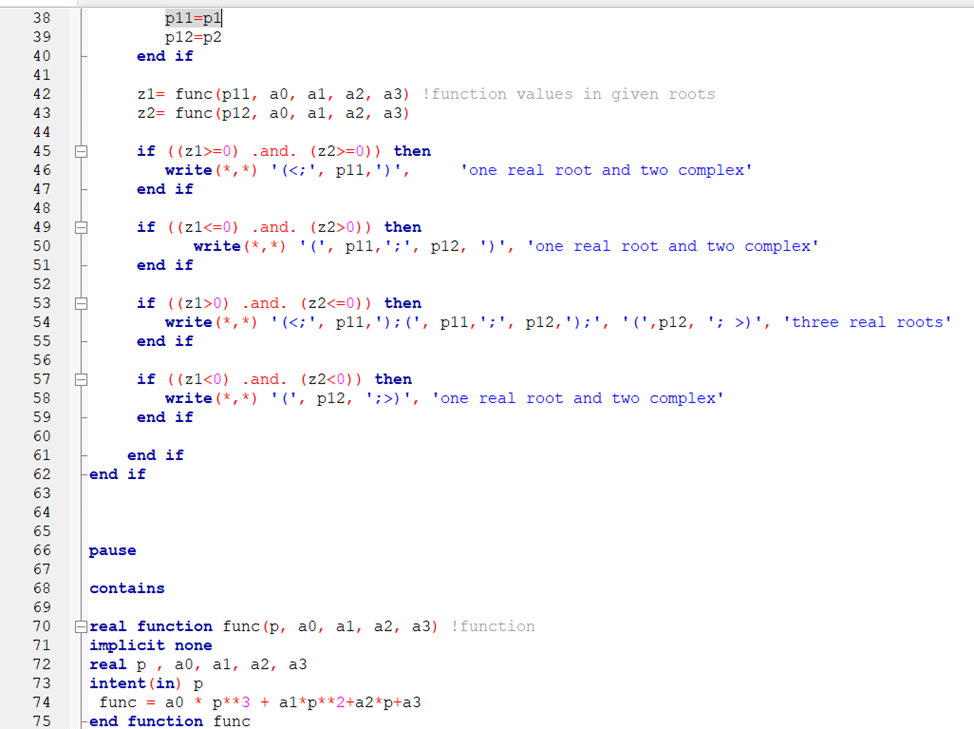 Текст программы: program lab1 implicit none real:: b0, b1, b2, d, p11, p12, p1, p2, z1, z2 real:: a0, a1, a2, a3 write(*,*) 'enter the coefficients of the equation(a0, a1, a2, a3)' read(*,*) a0, a1, a2, a3 b0=3*a0 b1=2*a1 b2=a2 d=b1*b1 - 4* b0*b2 !finding the discriminant if (d < 0) then ! case when the discriminant is less than zero write(*,*) 'no real roots' else if (d == 0) then ! the case when the discriminant is zero p1=-b1/(2*b0) !root of the equation if (func(p1, a0, a1, a2, a3) < 0) then !finding signs write(*,*) '(', p1, ';>)', 'one real root and two complex' else write(*,*) '(<;', p1, ')', 'one real root and two complex' end if end if if (d > 0) then !discriminant greater than zero p1=(-b1+sqrt(d))/(2*b0) !roots of the equation p2=(-b1-sqrt(d))/(2*b0) if (p1>p2) then ! sorting roots by range p11=p2 p12=p1 else p11=p1 p12=p2 end if z1= func(p11, a0, a1, a2, a3) !function values in given roots z2= func(p12, a0, a1, a2, a3) if ((z1>=0) .and. (z2>=0)) then write(*,*) '(<;', p11,')', 'one real root and two complex' end if if ((z1<=0) .and. (z2>0)) then write(*,*) '(', p11,';', p12, ')', 'one real root and two complex' end if if ((z1>0) .and. (z2<=0)) then write(*,*) '(<;', p11,');(', p11,';', p12,');', '(',p12, '; >)', 'three real roots' end if if ((z1<0) .and. (z2<0)) then write(*,*) '(', p12, ';>)', 'one real root and two complex' end if end if end if pause contains real function func(p, a0, a1, a2, a3) !function implicit none real p , a0, a1, a2, a3 intent(in) p func = a0 * p**3 + a1*p**2+a2*p+a3 end function func end program lab1 |
