контрольная работа ПРИКЛОДНАЯ МЕХАНИКА (Автосохраненный). Задание Привод бегунов для приготовления формовочной земли
 Скачать 337.39 Kb. Скачать 337.39 Kb.
|
 Задание: Привод бегунов для приготовления формовочной земли. Задание: Привод бегунов для приготовления формовочной земли.Исходные данные: Р4 = 16 кВт 4 = 2,5 рад/с Срок службы редуктора L = 20000 ч. Рассчитать быстроходную цилиндрическую ступень редуктора.  Привод бегунов для приготовления формовочной земли состоит из электродвигателя, двухступенчатого цилиндрического редуктора, выполненного по развернутой схеме и открытой конической зубчатой передачи, смонтированных на одной раме. Электродвигатель соединен с ведущим валом редуктора с помощью муфты. Выходной вал редуктора с валом барабана ленточного транспортера соединен также с помощью муфты. Муфты, примененные здесь, относятся к упругим компенсирующим муфтам. Называемая муфта упругая втулочно-пальцевая ГОСТ 21424-75 (МУВП). Муфта применяется для соединения соосных валов и передачи номинального вращающего момента от 6,3 до 16000 Нм и уменьшения динамических нагрузок; диаметры валов от 9 до 160 мм. Муфты данного типа обладают большой радиальной и угловой жесткостью. Муфта состоит из двух чугунных полумуфт, в отверстиях которых закреплены стальные пальцы с надетыми на них кольцами и резиновыми гофрированными втулками. Металлический контакт полумуфт отсутствует, что обеспечивает плавную работу муфт и электрическую изоляцию валов. Посадочные отверстия для валов могут быть цилиндрическими или коническими. Муфты упругие втулочно-пальцевые получили широкое распространение благодаря относительной простоте конструкции и удобству замены упругих элементов. Зубчатый или червячный передаточный механизм, представляющий собой систему зубчатых колес в отдельном закрытом корпусе, непроницаемом для пыли и одновременно являющемся масляной ванной  для механизма, называется редуктором. для механизма, называется редуктором.Назначение редуктора – понижение угловой скорости и повышение вращающего момента ведомого вала по сравнению с валом ведущим. Звенья редукторной передачи делают из высококачественных материалов с повышенным классом точности. Это объясняется, прежде всего, тем, что зубчатые передачи редукторов защищены от пыли и грязи, хорошо смазываются, а поэтому менее повреждены абразивному износу, истиранию, заеданию и при изготовлении из высококачественных материалов длительное время сохраняют первоначальную точность. Кроме того, колеса в закрытых передачах проверяются на контактную прочность, которая у высококачественных материалов в 15-20 раз выше, чем у низкокачественных. Размещение опор валов редуктора в одном общем жестком корпусе обеспечивает постоянство относительного расположения осей валов, а это позволяет применять широкие зубчатые колеса с малым модулем. Применение малых модулей в свою очередь приводит к увеличению точности и уменьшению шума при работе передачи, к снижению стоимости ее изготовления. Автоматическая смазка способствует малому износу и высокому КПД редукторной передачи. Наличие кожуха обеспечивает безопасность работы редукторов. Этими положительными качествами объясняется широкое применение редукторов в современном машиностроении и вытеснение ими открытых передач. Крутящий момент от двигателя передается на входной или ведущий  вал редуктора через соединительную муфту. От выходного или ведомого вал редуктора через соединительную муфту. От выходного или ведомоговала крутящий момент передается на вал ведущий шестерни открытой конической передачи также через соединительную муфту. Недостатком развернутой схемы редуктора является несимметрическое расположение зубчатых колес (шестерни) относительно опор, что вызывает неравномерное распределение давления на подшипники и появление осевых усилий, нагружающих подшипники колес первой ступени. Кроме того, при изгибе валов редуктора зубчатые колеса тяжело нагруженной второй ступени оказываются расположенными на наклонных участках валов, что ведет к неравномерному распределению нагрузки вдоль зуба. Эти недостатки устраняются применением схемы, у которой первая ступень раздвоена на две пары колес с противоположно направленными зубьями.  Выбор электродвигателя. Определим общий КПД привода. 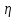 = =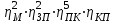 , ,где ηМ – КПД муфты, ηМ ≈ 0,98. [1, табл.1] ηЗП – КПД одной пары зубчатой передачи, принимаем ηЗП ≈ 0,95. [1, табл.1] ηПК – КПД одной пары подшипников кочения, принимаем ηПК ≈0,99 . [1, табл.1] ηКП – КПД одной пары конической передачи, ηПК ≈ 0,92. [1, табл.1] η = 0,982 ∙ 0,952 ∙ 0,995 ∙ 0,92 =0,758 Определим требуемую мощность двигателя по формуле: η= 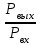 = =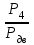 отсюда требуемая мощность двигателя: Ртр.мощ.дв.= 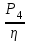 = =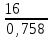 =21,10 кВт. =21,10 кВт.Определим требуемую частоту вращения вала двигателя по формуле: ДПдв = iред. ∙nвых.=i1 ∙ i2 ∙ i3 ∙ n4 i1 - передаточное отношение первой ступени закрытой цилиндрической передачи, принимаем i1= от 4 до 6. [1, табл.2] i2 - передаточное отношение второй ступени закрытой цилиндрической передачи, принимаем i2= от 4 до 6. [1, табл.2] i3 - передаточное отношение третий ступени открытой конической передачи, принимаем i3= от 1 до 2. [1, табл.2] n4 = 10 ∙ 4 = 10 ∙ 2,5 = 25  ДПдв = (4-6) ∙ (4-6) ∙ (1-2) ∙ 25 = 400 ….. 1800 об/мин. ДПдв = (4-6) ∙ (4-6) ∙ (1-2) ∙ 25 = 400 ….. 1800 об/мин.Принимаем по таблице [1, П1] электродвигатель асинхронный серии 4А 200М6 с мощностью Рдв = 22 кВт, nдв = 1000 об/мин. 3. Кинематический расчет. Определим передаточное отношение редуктора по формуле: iр = 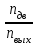 = = 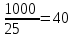 Производим разбивку данного передаточного отношения по ступеням. Передаточное отношение привода: iр = i1 ∙ i2 ∙ i3 = 5 ∙ 4 ∙ 2 = 40 i1 – передаточное отношение быстроходной ступени редуктора. [1, стр.6] i2 – передаточное отношение тихоходной ступени редуктора. [1, стр.6] i3 – передаточное отношение открытой конической передачи, [1, стр.6] Принимаем:i1 = 5,0; i2 = 4,0; i3 = 2,0.  4. Определение крутящих моментов на валах с учетом КПД. 4. Определение крутящих моментов на валах с учетом КПД. 1) Вал двигателя. Частота вращения вала: nдв = 1000 об/мин. Угловая скорость вала: дв = 100 рад/с. Вращающий момент вала двигателя: Мдв = 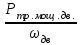 = = 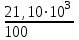 = 211,0 Н∙м = 211,0 Н∙м2) Ведущий вал редуктора: n1 = 1000 об/мин. 1 = 100 рад/с. Р1 = Рдв ∙ ηМ ∙ ηПК = 21,10 ∙ 0,98 ∙ 0,99 = 20,47 кВт. М1 = 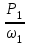 = = 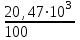 = 204,7 Н∙м = 204,7 Н∙м3) Промежуточный вал редуктора: i1 = 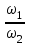 => 2 = => 2 = 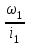 2 = 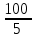 = 20 рад/с. = 20 рад/с.n2 = 20 ∙ 10 = 200 об/мин. Р2 = Р1 ∙ ηПК ∙ ηЗП = 20,47 ∙0,99 ∙ 0,95 = 19,25 кВт. М2 = 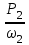 = = 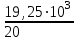 = 962,5 Н∙м = 962,5 Н∙м 4) Выходной вал редуктора. 4) Выходной вал редуктора.i2 = 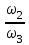 => 3 = => 3 = 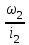 3 = 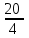 = 5 рад/с. = 5 рад/с.Р3 = Р2 ∙ ηЗП ∙ ηПК = 19,25 ∙ 0,95 ∙ 0,99 = 18,10 кВт. М3 = 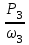 = = 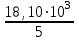 = 3620 Н∙м = 3620 Н∙мВал ведущий конической передачи. i2 = 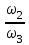 => 3 = => 3 = 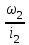 3 = 5рад/с. 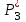 = Р3 ∙ ηМ ∙ ηПК = 18,10 ∙ 0,98 ∙ 0,99 = 17,56 кВт. = Р3 ∙ ηМ ∙ ηПК = 18,10 ∙ 0,98 ∙ 0,99 = 17,56 кВт.М3 = 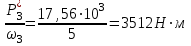 6) Вал бегунов. i3 = 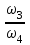 => 4 = => 4 = 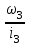 4 = 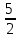 = 2,5 рад/с. = 2,5 рад/с.Р4 = Р3 ∙ ηПК ∙ ηКП = 17,56 ∙ 0,99 ∙ 0,92 = 16 кВт. М4 = 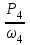 = = 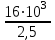 = 6400 Н∙м. = 6400 Н∙м. 5. Предварительный расчет валов по передаваемым моментам. 5. Предварительный расчет валов по передаваемым моментам.1) Вал двигателя. Для определения диаметра выходного вала: 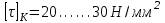 Для определения промежуточного вала под колесом 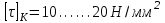 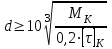 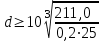 = 34,8 мм. = 34,8 мм.2) Ведущий вал. 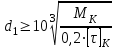 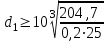 = 34,4 мм. = 34,4 мм.3) Промежуточный вал. 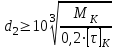 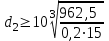 = 50,5мм. = 50,5мм.4) Выходной вал. 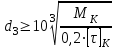  = 89,9 мм. = 89,9 мм. 5) Вал бегунов. 5) Вал бегунов.  = 108,6 мм. = 108,6 мм.6. Расчет быстроходной цилиндрической ступени редуктора. Исходные данные: Крутящий момент на валу шестерни: М1 = 204,7 ∙103 Н∙мм Крутящий момент на валу колеса: М2 = 972,5 ∙103 Н∙мм Частота вращения шестерни: n1 = 1000 об/мин. Передаточное число: u12 =5 Срок службы передачи: L = 20000 ч. 2.1.1 По таблице 1принимаем для шестерни – 40Х, термообработка – улучшение НВ 250, σн limb1 = 560 МПа, Sн1 = 1,1; σ0Flimb2= 440 МПа, SF1 = 1,6; для колеса – сталь 45, термообработка – нормализация НВ=200, σн limb2 = 455 МПа, Sн2 = 1,1; σ 0Flimb2 = 350 МПа, SF2 = 1,65. Определяем допускаемое напряжение: [σн]i= (σн lim bi / Sнi) ·KнLi·[σk]i = (σ0F lim bi/SF i) · KFCi · KFLi , где i = 1 –для шестерни, i = 2 –для колеса; σнlimbi- предел контактной выносливости; σFlimbi- предел выносливости на изгиб при отнулевом цикле изменения напряжений; Sнi- коэффициент безопасности при расчете на контактную прочность зубьев; SFi - коэффициент безопасности при расчете зубьев на изгиб.  Рассчитываем допускаемые напряжения с учетом фактических условий нагружения. Базовое число циклов напряжений: NHO1 = 30 НВ2,4 = 30 · 2502,4 = 1,7 · 107; NHO2 = 30 · 2002,4 = 9,9 · 106 ; NFO1 = NFO2 = 4 · 106 Время работы передачи за весь срок службы: tΣ = 20000 ч. Число циклов напряжений: NHE1 = NFE1 = 60 · n1 · tΣ = 60 · 1000· 20000 = 1,2 · 108 NHE2 = NFE2 = 60 · n1 · tΣ/ i1,2 =60 · 1000 · 20000 / 5 = 2,4 · 108 Коэффициенты долговечности KHL1 = KHL2 =1, так как NHE1 > NHO1 и NHE2 >NHO2 ; KFL1 =KFL2 =1, так как NFE1>NFO1 и NFE2>NFO2. Коэффициенты KFC1=KFC2=1 для нереверсивной передачи. где ni - частота вращения зубчатого колеса, об/мин; tΣ, – время работы передачи за срок службы (ресурс передачи), часы. Допускаемые контактные напряжения: [σн]1= (σн lim b1 / SH1) · KHL1 = (560 / 1,1) · 1= 509 МПа, [σн]2= (σн lim b2 / SH2) · KHL2 = (455 / 1,1) · 1= 414 МПа. Допускаемые напряжения при изгибе: [σF]1= (σ 0F lim b1 / SF1) · KFC1 · KFL1 = (440/ 1,6) · 1 · 1= 275 МПа, [σF]2= (σ0F lim b2 / SF2) · KFC2 · KFL2 = (350/ 1,65) · 1 · 1= 212 МПа. 2.1.3 Определяем числа зубьев шестерни, колеса и передаточное число. Принимаем угол наклона линии зуба β = 11º. Число зубьев шестерни по условию неподрезания:  Z1 >17cos³β =17cos³11º=16,08. где i12 – требуемое передаточное отношение передачи (отношение угловых скоростей шестерни и колеса); β - угол наклона линии зуба, принимается для косозубых колес в интервале (8…15º), для шевронных – (25…45º) Принимаем Z1 = 16. Число зубьев колеса Z2 = Z1 · i12 = 16 · 5 = 80, принимаем Z2= 8. Передаточное число: u = Z2 / Z1 = 80/16 = 5. 2.1.4. Определяем требуемое межосевое расстояние передачи из условия контактной прочности. аW = (u+1){0,78·М2·КН·cosβ·Е1·Е2/ ([σН]·u)²·Ψbа·(Е1+Е2)}1/3 где М2 – крутящий момент на колесе, Н·мм; Ψbа – коэффициент ширины зубчатого колеса, выбирается по таблице 2; Кн - коэффициент нагрузки, учитывающий дополнительные вредные нагрузки, сопутствующие работе передачи; предварительно принимается Кн = 1,2 для колес с твердостью поверхностей зубьев < НВ 350 и Кн = 1,35 для колес с твердостью НВ 350; Е1, Е2 – модули упругости первого рода соответственно материала шестерни и колеса; [σн] - расчетное допускаемое контактное напряжение; u – передаточное отношение ступени. аW =(5+1){0,78·972500·1,2·cos110·2,1·10 5∙2,1·10 5/(414∙5)²·0,25·(2,1∙2,1)∙105}1/3=266,46мм. Коэффициент нагрузки предварительно принимаем Кн = 1,2; Е1=Е2 = 2,1·10 5 Мпа  Расчетное допускаемое напряжение: Расчетное допускаемое напряжение: [σн]= [σн]min= [σн]2= 414 МПа. Коэффициент Ψbа с учетом твердости < НВ 350 и несимметричного расположения колес относительно опор по таблице 2 принимаем Ψbа=0,250. 2.1.5. Определяем нормальный модуль передачи: mn = (2 · aw · cosβ)/(Z1 + Z2) = 2 ·266,46 ·cos11º (16+80) = 5,4 мм. По таблице 3 принимаем стандартное значение модуля mn = 5,5 мм. 2.1.6. Уточняем межосевое расстояние передачи: аw = 0,5(Z1+Z2)mn /cosβ = 0,5(16+80) 5,5/cos11º = 269,4 мм. За уточненное значение принимаем целую часть аw = 269 мм. 2.1.7. Уточняем угол наклона линии зуба: β=arccos[0,5(Z1+Z2)mn/аw]=arccos0,5(16+80)5,5/269=11,058º =11º3´29″. 2.1.8 Рассчитываем геометрические параметры зубчатой передачи. Делительные параметры: d1 = mn · Z1 / cosβ = 5,5 · 16 / cos 11º3´29″ = 89,795 мм; d2 = mn · Z2 / cosβ = 5,5· 80 / cos 11º3´29″ = 448,979 мм. Диаметры вершин: da1 = d1 + 2· mn = 89,795 + 2· 5,5 = 100,795 мм; da2 = d2 + 2· mn = 448,979 + 2 · 5,5 = 459,979 мм. Диаметры впадин: df1 = d1 - 2,5 · mn= 89,795 – 2,5 · 5,5 = 76,045 мм; df2 = d2 - 2,5 · mn = 159,288 – 2,5 · 2,75 = 152,413 мм. Ширина колеса b2 = Ψba · аw = 0,25 · 269,4 = 67,35 мм,  принимаем b2 = 67мм. Ширина шестерни b1 = 1,12 · b2 = 1,12 ∙ 269 = 75мм. Коэффициент ширины шестерни: Ψbd= b2 / d1 = 67 / 89,795 = 0,74. 2.1.9. Определяем окружную скорость на делительном диаметре зубчатых колес: V = (π ·d1·n1)/60 000 = (π·89,795·1000)/60 000 = 4,69 м/с. где n1 – частота вращения шестерни, об/мин. 2.1.10. Выбирается степень точности зубчатой передачи в соответствии с окружной скоростью V и рекомендациями, приведенными в таблице 5. 2.1.11. Уточняется значение коэффициента нагрузки Кн Кн = Кнα · Кнβ · Кнv , где Кнα – коэффициент, учитывающий распределение нагрузки; для прямозубых колес Кнα = 1, для косозубых и шевронных определяется по таблице 6; КНβ – коэффициент, учитывающий концентрацию нагрузки, определяется по таблице 7; КНV– коэффициент, учитывающий динамичность приложения нагрузки, определяется по таблице П8. Кнα= 1,09 по таблице П6; КНβ= 1,08 по таблице П 7; КНV= 1,04 по таблице П8. 2.1.12. Производится проверочный расчет контактных напряжений на рабочих поверхностях зубьев :  σН=Zε{4,35·Е1·Е2·cosβ·М2·КНα·КНβ·КНv(u+1)/(Е1+Е2)·d22·b2}1/2≤[σН], где Zε– коэффициент, учитывающий суммарную длину контактных линий; для прямозубых колес при α = 20º, Zε= 0,9 для косозубых и шевронных Zε = 0,8. Если полученное в результате расчета контактное напряжение меньше или превышает допускаемое напряжение [σН] не более, чем на 3%, т.е. Е = (σН - [σН])/ [σН] · 100% < 3%, то прочность зубчатой передачи по контактным напряжениям считается обеспеченной. σН=0,8{4,35·2,1·105∙2,1∙105·cos11º3´·972500·1,09·1,08·1,04(5+1)/(2,1+2,1)·105∙ ∙(448,979)2 ·67}1/2 = ≤[σН]= 414 МПа. 2.1.13.Определяются силы, действующие в зацеплении зубчатых колес: Окружная сила: Ft = 2 М2/ d2 = 2 ∙ 972500/448,979 = 4332 Н. Радиальная сила: Fr= Ft · tgα / cosβ = 4332 ∙ tg20º/ cos 11º3´29″ = 1609 Н. Осевая сила: Fa = Ft · tg β = 4332 ∙ tg11º3´29″ = 789,72 Н. 2.1.14. Определяем коэффициенты формы зубьев шестерни YF1 и колеса YF2 YF1 = 4,28 по таблице 9 для ZV1 = Z1 · cos³β = 16 / cos³ 11º3´29″ = 14,46; YF2= 3,65 по таблице 9 для ZV2 = Z2 · cos³β = 80 / cos³ 11º3´29″ = 72,34. 2.1.15. Определяем коэффициент наклона зуба:  Yβ= 1- β / 140 = 1 – 11,058/140 = 0,921. 2.1.16. Определяем коэффициенты нагрузки для расчета напряжений изгиба зубьев: КFα = 0,91 – по таблице П 10; КFβ = 1,17 – по таблице П 11; КFv = 1,11 – по таблице П 12. 2.1.17. Определяем отношения [σF]/YF: [ σF]1 / YF1 = 275 / 4,28 = 64,25 МПа; [ σF ]2 / YF2 = 212 / 3,65 = 58,08 МПа. 2.1.18. Производим проверочный расчет напряжений изгиба в опасном сечении зубьев колеса, т.к. должно быть {[σF]2 /YF2} < {[σF]1 /YF1 } σА = (НА2·Нβ·Ае ·КАα·КАβ·КАм).(и2·ьт) σА = (3,65·0,921·4332·0,91·1,17·1,11)/(67·5,5) = 12,80 МПа; σF = 12,80 МПа < [σF]2 = 212 МПа. 2.1.19. С целью обеспечения большей равнопрочности передачи и увеличения Z1 и Z2 уменьшаем mnпри том же значении аw. Принимаем по таблице 3 стандартное значение mn = 3,0 мм. 2.1.20. Определяем суммарное число зубьев: ZΣ = Z1 + Z2 ZΣ= 2 · аW · cosβ / mn = 2 · 269 · cos 11º3´29″ / 3,0= 175,75. 2.1.21. Определяем числа зубьев шестерни и колеса: Z1 = ZΣ / ( i12 +1) = 175,75 / 5 + 1 = 29,15, принимаем Z1 = 29. Z2 = Z1 · i12 = 29 · 5 = 145,  принимаем Z2 = 145. 2.1.22. Определяем передаточное число: u = Z1 / Z2 = 145 / 29 = 5. 2.1.23. Уточняем угол наклона линии зуба: β = arccos [ 0,5 (Z1 +Z2) mn / аW] = arcos [ 0,5 (29 + 145) · 3 / 269 ] = 11,573747º = 11º3′29″. 2.1.24. Рассчитываем геометрические параметры зубчатой передачи: d1 = mn · Z1 / cosβ = 3 · 29 / cos 11º3′29″ = 88,775 мм; d2 = mn · Z2 / cosβ = 3 · 145 / cos 11º3′29″= 441,714 мм; da1 = d1 + 2 · mn = 88,775 + 2 · 3 = 94,775 мм; da2 = d2 + 2 · mn =441,714 + 2 · 3 = 447,714 мм; df1= d1 – 2,5 · mn = 88,775 – 2,5 · 3 = 81,275; df2= d2 – 2,5 · mn= 441,714 – 2,5 · 3 = 434,214 мм; b2 = 67мм, b1 = 75мм, Ψbd = 0,75. 2.1.25. Повторяем проверочный расчет контактных напряжений: σН=0,8{[4,35·2,1·105·2,1·105cos11º3´·972500·1,09·1,06]/[(2,1+2,1)105·(441,714)²·67]}1/2= = {1,04(5+1)}1/2 = МПа < [σН] = 414 МПа. 2.1.26. Определяем силы в зацеплении: Ft= 2 · М2/ d2 = 2 · 972500 / 441,714 = 4403,30 Н; Fr = Ft · tg α / cos β = 4403,30 · tg 20º / cos 11º3´29″ = 1627,53 Н; Аф = Ft · tg β = 4403,30 · tg 11º3´29″ = 802,72 Н. 2.1.27. Определяем коэффициенты зубьевYF1 иYF2 YF1 = 3,90 ZV1 = Z1 cos3β = 29 cos311º3´29″ = 26,5;  YF2 = 3,60 ZV2= Z2 cos3β = 145 cos3 11º3´29″ = 94,1. 2.1.28. Определяем коэффициент наклона зуба: Yβ = 1- β/140 = 1 – 11,57374 / 140 = 0,917. 2.1.29. Определяем коэффициенты нагрузки: КFα = 0,91; КFβ = 1,12; КFV=1,11. Определяем отношения: [σF]1 / YF1 = 275 / 3,90 = 70,51 МПа; [σF]2 / YF2 = 212 / 3,60 = 58,88 МПа. Повторяем проверочный расчет напряжений изгиба в опасном сечении зубьев колеса, т.к. σF = (3,60·0,917·4403,30·0,91·1,12·1,11)/(67·3) = 81,81 МПа. Сравниваем полученное значение с допускаемым напряжением изгиба: σF = 81,81 МПа < [σF ]2 = 212 МПа и видим, что условие прочности на изгиб выполняется, что даёт нам основание считать выполненные расчёты верными. |
