парные линейные задание. Контрольные.МУ.Парный линейный.34с.. Заказ Тираж Цена свободная Издательство Тюменского государственного нефтегазового университета. Тюменский государственный нефтегазовый университет, ризограф литература Айвазян С. А. Статистическое исследование
 Скачать 0.72 Mb.
|
|
2. Выполняем вычисления аналогичные прямой регрессии. Коэффициенты уравнения обратной регрессии статистически значимы. Получили уравнение обратной регрессии X = b0 (ху) + b1 (ху) У = -3,55 + 1,43 У. X1р = -3,55 + 1,43 х5,0 = 3,6 ;  X1 = 1,5 – 3,6 = - 2,1; X12 = 4,41;X2р = -3,55 + 1,43 х4,5 = 2,855 и т.д.; 3. Наносим линию обратной регрессии на график (рис. 2), указываем на графике величины коэффициентов обратной регрессии. Линия обратной регрессии круче линии прямой регрессии, обе линии пересекаются в центре массива экспериментальных данных  = 7,44 и  = 7,69.3.4.3. Корреляция Вычисляем коэффициент парной корреляции  = 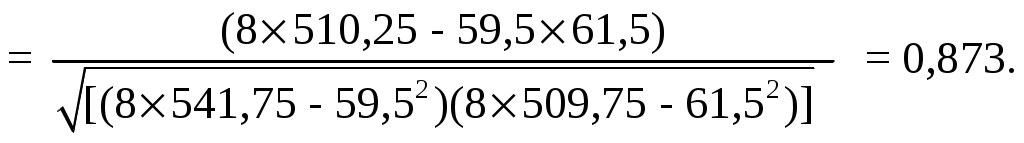Проверка r = Qху / (Qх Qу)0,5 = 52,84/(99,22х36,97)0,5 = 0,87. 2. Проверяем правильность вычислений по коэффициенту детерминации и произведению угловых коэффициентов регрессии. r2 = b1 (ух) b1 (ху) = 0,53х1,43 = 0,76; r = 0,760,5 = 0,87. Коэффициент детерминации r2 = 0,76 (76%) показывает процент разброса - изменчивости искомой величины Y относительно среднего значения, определяемого изменчивостью фактора Х. 27 Если выполняется условие  , то уравнение регрессии статистически значимо описывает результаты эксперимента. Для рассмотренного случая при 5%-ном уровне значимости уравнение неадекватно описывает результаты опытов. При 10%-ном уровне значимости табличное значения критерия Фишера составит 3,0145. В этом случае условие , 3,59 > 3,0145 выполняется. Уравнение прямой регрессии адекватно описывает результаты опытов при 10%-ном уровне значимости. 3.4.2. Обратная регрессия 1. Вычисляем коэффициенты уравнения линии обратной регрессии: 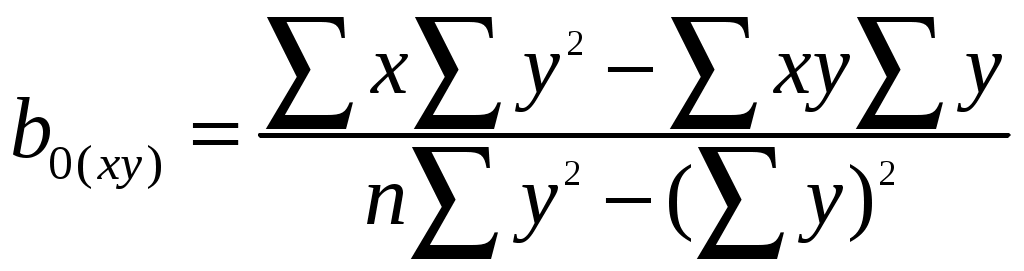 = 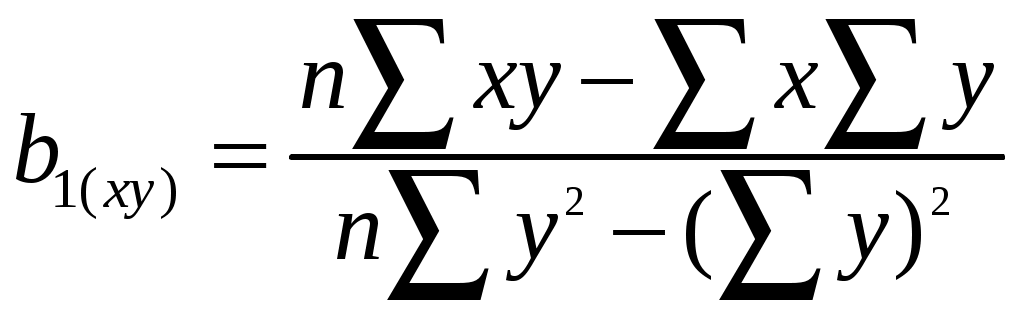 = 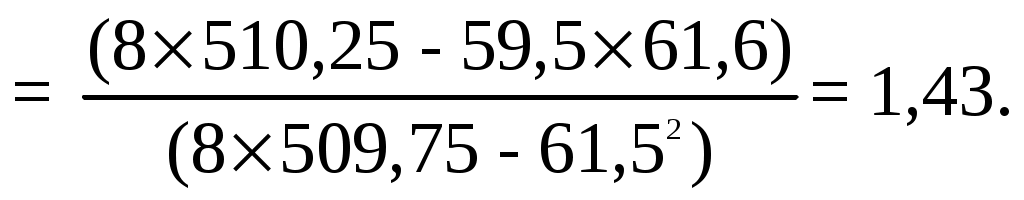Проверка: b1 (ху) = Qху / Qу = 52,84/36,97 = 1,43; b0 (ху) = - b1 (ху) = 7,44 – 1,43х7,69 = -3,55.26 3. ПАРНЫЙ ЛИНЕЙНЫЙ РЕГРЕССИОННЫЙ И КОРРЕЛЯЦИОННЫЙ АНАЛИЗ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ 3.1. Основные определения Подавляющее большинство формул, используемых в технических дисциплинах, относятся к так называемым "парным" зависимостям типа  .Задача обработки данных заключается в аналитическом представлении искомой функциональной зависимости, т. е. в подборе формулы, описывающей результаты эксперимента. Особенность задачи состоит в том, что наличие случайных ошибок измерения (или как говорят наличия “шума“ в эксперименте), при описании результатов, не должно включать все опытные значения. Другими словами, график искомой функции не должен проходить через все точки (соединять их), а должен по возможности сглаживать “шум" – плавная линия (в нашем случае прямая) должна проходить в области расположения точек. Регрессионный анализ дает возможность получить математическую модель объекта исследования - уравнение, аналитическое представление функциональной зависимости одной величины y от другой величины x. Линейный регрессионный анализ, при помощи метода наименьших квадратов (МНК), состоит в том, что, зная положение экспериментальных точек на плоскости, нужно так провести линию регрессии, чтобы сумма квадратов отклонений вдоль выбранной оси координат от этих точек до проведенной линии регрессии была бы минимальной. Для проведения регрессионного анализа по МНК предъявляется следующее требование: уравнение должно быть линейным по параметрам или допускать возможность линеаризации - спрямления. В этом случае получим уравнение прямой регрессии в декартовых координатах - У = b0(yх) + b1(yх) Х . Также иногда применяют обратную регрессию - Х = b0(xy) + b1(xy) У где: b0 (yх) - свободный член уравнения регрессии; 11 геометрически он представляет собой расстояние от начала координат до точки пересечения линии прямой регрессии с ординатой (это отрезок, отсекаемый на ординате линией регрессии); (yх) – У относительно Х или У от Х. Для обратной регрессии b0 (xy) - это отрезок на абсциссе, отсекаемый этой прямой; (xy) - Х относительно У или Х от У . b1(yх) – угловой коэффициент уравнения прямой регрессии - тангенс угла наклона линии прямой регрессии к оси абсцисс, b1(xy) - угловой коэффициент уравнения обратной регрессии - тангенс угла наклона линии обратной регрессии к оси ординат. Корреляционный анализ изучает усредненный закон поведения каждой из величин в зависимости от значений другой величины, а также меру зависимости (тесноту взаимосвязи) между рассматриваемыми величинами. Корреляция между величинами x и y называется линейной, если обе функции регрессии (y от x и x от y) линейны. Угловые коэффициенты этих прямых выражаются через коэффициент корреляции, который также служит мерой линейной зависимости между величинами. Мера зависимости между величинами характеризуется коэффициентом корреляции  (для прямых) или корреляционным отношением  (для нелинейных зависимостей - кривых).Коэффициент корреляции представляет собой безразмерную величину, значение и знак которой характеризуют направление и величину подобной взаимосвязи между y и x. Значения коэффициента корреляции могут изменяться от -1 до +1, включая 0. Коэффициент корреляции, равный +1 или -1, указывает на наличие строгой функциональной (детерминированной, ортогональной) взаимосвязи. 0 - говорит об отсутствии какой бы то не было взаимосвязи. Коэффициент корреляции, отличный от 1, указывает на случайную (стохастическую) взаимосвязь. Знак коэффициента указывает на направление взаимосвязи между двумя переменными. Этот знак (+ или -) соответствует знаку углового коэффициента b1(yх). 12 Ур1 = b0 (ух)+ b1 (ух)X = 3,73 + 0,53х1,5 = 4,53; Y1 = У1 эк - У1 р = 5,0 – 4,53 = 0,47; Y12 = 0,2209;У2р = 3,73 + 0,53 х 4,0 = 5,85; Y2 = У2 эк - У2 р = 4,5 – 5,85 = -1,35; Y22 = 1,8225 и т.д. =0,2209+1,8225+0,3844+0,8836+1,5876+0,0009++2,0736+1,8225= 8,796. 8. Вычисляем остаточную дисперсию, характеризующую ошибку предсказания результатов опытов по уравнению прямой регрессии  =  9. Определяем общую дисперсию:  = 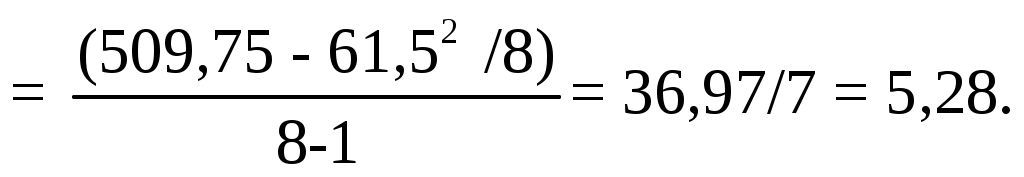10. Проверяем адекватность (статистическую значимость) уравнения регрессии по F-критерию Фишера (табл. 2 Приложения). Адекватность уравнения характеризует его способность предсказывать результаты последующих опытов.  ,5,28/1,47 = 3,59 < 4,207. где  ,  - число степеней свободы. Табличное значение критерия Фишера (4,207) определено при 5%-ном уровне значимости.25 6. Наносим линию прямой регрессии на график (рис.2), указываем на графике величины коэффициентов прямой регрессии. 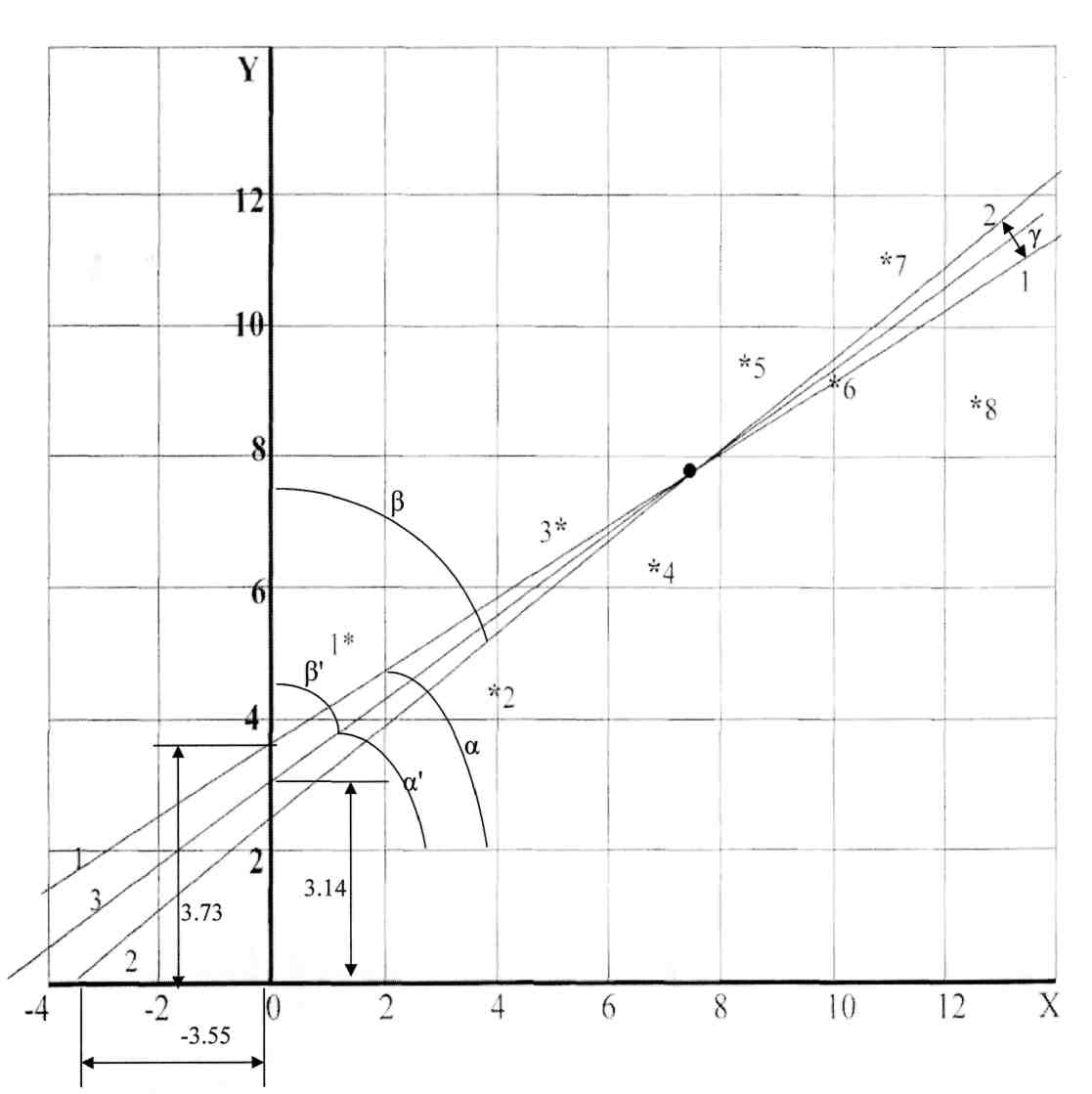 Рис.2. Линии прямой (1), обратной (2) и ортогональной (3) регрессии по методу наименьших квадратов 7. Определяем расчетные значения по уравнению прямой регрессии - расчетные значения должны находиться на линии регрессии. Вычисляем отклонения между экспериментальными и расчетными величинами, а также квадраты этих отклонений и заполняем таблицу 2 24 Абсолютное значение коэффициента (без учета знака) характеризует силу или тесноту взаимосвязи. Уравнение прямой линии может быть получено различными способами: методом Асковица, методом группировки /14/, методом средних /3,7,11/, методом наименьших квадратов (МНК) и т.д. Выполним обработку условных экспериментальных данных несколькими методами, начиная с простейшего. 3.2. Метод группировок Этот метод является наиболее простым. Для применения этого метода необходимо знать хотя бы одну точку прямой, так как определяется только угловой коэффициент. Построение прямой производится очень быстро. Если задан ряд экспериментальных точек с координатами Х и Y, то угловой коэффициент прямой, принадлежащей этим точкам, можно вычислить по формуле  где Х и Y – координаты m точек, сгруппированных в одной части графика, а Х’ и Y’ – координаты m точек, сгруппированных в другой части графика. Если интервалы между значениями Х примерно одинаковы, то имеющиеся данные необходимо разделить на три примерно равные группы и использовать группу точек с координатами Х и Y, находящихся в верхней части графика, и группу точек с координатами Х’ и Y’, находящихся в нижней части графика, исключив среднюю группу точек. В этом случае нарушается общее практическое правило статистического анализа: «Статистический критерий оказывается наиболее эффективным при использовании всех данных». Например, имеем 8 пар измерений, n = 8: Y : 9,0; 11,0; 9,0; 9,5; 6,5; 7,0; 4,5; 5,0. Х : 12,5; 11,0; 10,0; 8,5; 7,0; 5,0; 4,0; 1,5. 13 Эти исходные данные и результаты статистической обработки сводим в таблицу 2. В таблице 2 приведены результаты статистической обработки этих данных и другими методами. Для контрольной работы надо приготовить таблицу для 10 точек. Наносим точки на график – рис.1. Делим массив данных на три примерно равные группы: выделяем по три точки в верхней и нижней части графика (первые три и последние три пары значений), две точки в средней части не используем. 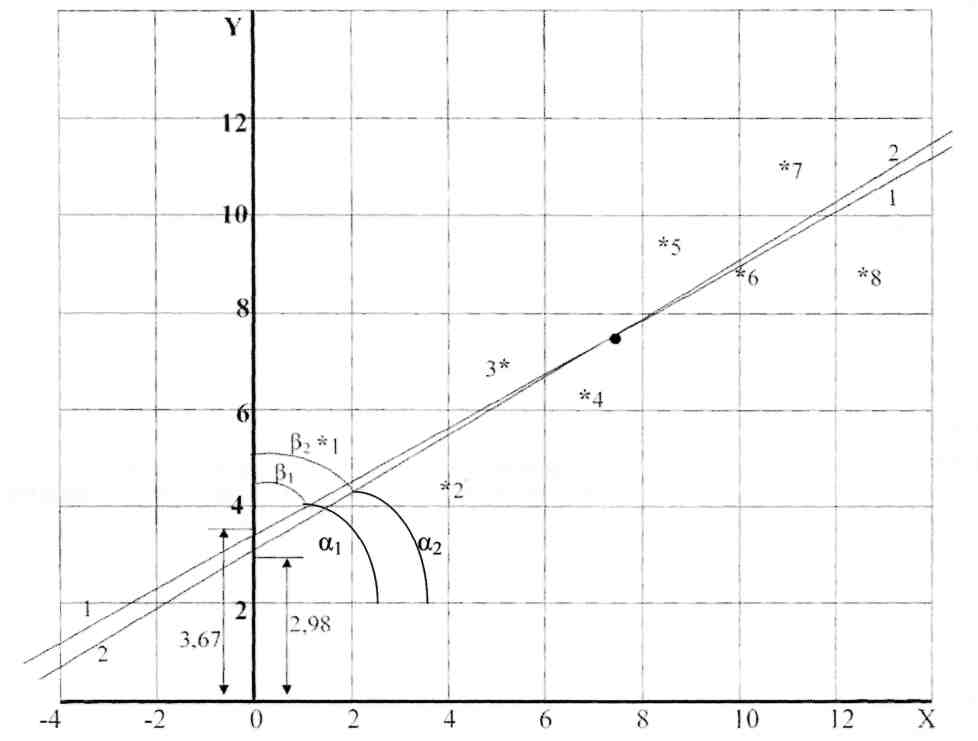 Рис. 1. Линии регрессии по методу группировок (1) и методу средних (2) 14 3. Проверяем правильность вычислений  2072 – 1212/8 = 99,22 + 36,97 + 2×52,84; 241,87 = 241,87. b1 (ух) = Qху / Qх = 52,84/99,22 = 0,53; b0 (ух) = - b1 (ух) = 7,69 – 0,53×7,44 = 3,73 = 1,008/0,122 =  ; 8,2 = 8,2. 4. Проверяем статистическую значимость коэффициентов регрессии по критерию Стъюдента 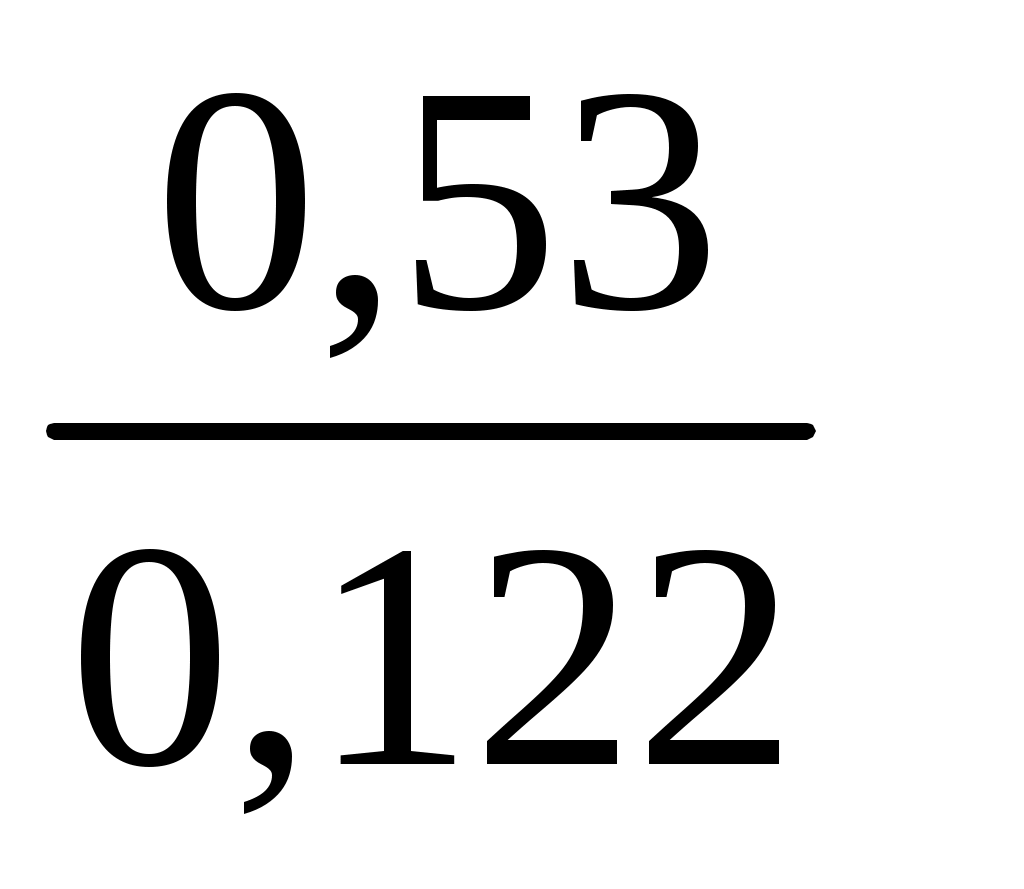 =  = 3,73 > 2,447, =  = 4,34 > 2,447.Если расчетные значения больше табличных  , то коэффициенты регрессии статистически значимы. Если расчетное значение меньше табличного, коэффициент исключается из формулы. Табличное значение критерия определяем из табл. 1 Приложения при заданном уровне значимости (5%) и числе степеней свободы f=n-2. Для нашего случая расчетные значения обоих коэффициентов регрессии больше табличных значений – коэффициенты регрессии статистически значимы. 5. Записываем уравнение прямой регрессии с учетом статистической значимости коэффициентов. Ур = b0 (ух)+ b1 (ух)X = 3,73 + 0,53 Х. 23 3.4.1. Прямая регрессия 1. Вычисляем коэффициенты уравнения линии прямой регрессии:  = =   ==  2. Определяем промежуточные величины для проверки значимости коэффициентов регрессии и оценки адекватности уравнения:  = 541,75 – (59,52/8) = 99,22;  = 509,75 – (61,52/8) = 36,97;  = 510,25 – (59,5х61,5)/8 = 52,84;  = 36,97 – 0,53х52,84 = 8,96; =  = 1,22;  =  = 1,22 / = 0,122.22 1. Определяем угловой коэффициент уравнения прямой регрессии b1(yх) =  = [(9,0+11,0+9,0) – (7,0+4,5+5,0)] / [(12,5+11,0+10,0) – (5,0+4,0+1,5)] = (29,0-16,5)/(33,5-10,5) = 12,5/23 = 0,543.Прямая должна проходить по опорной точке, расположенной в центре массива данных и имеющей координаты: Х ср =  /n = 59,5/8 = 7,44 и Yср =  /n = 61,5/8 = 7,69.В уравнение прямой У = b0(yх) + b1(yх) Х подставляем рассчитанные значения Х ср и Yср, получим 7,69 = b0(yх) + 0,54х 7,44. 2. Определяем свободный член уравнения прямой регрессии b0(yх) = Yср - b1(yх) Х ср = 7,69 - 0,54х 7,44 = 3,67. Получили искомое уравнение прямой регрессии |