экзамен по ттд. Закон Бойля Мариотта

• Название: Закон Бойля Мариотта
• Анкор: экзамен по ттд
• Дата: 13.02.2022
• Размер: 1.13 Mb.
• Имя файла: Ekz_-_TTD.docx
• Тип: Закон; #360257

1. 
   Понятие об идеальном газе. Основные законы идеальных газов.
   

Идеальным газом называется газ, в котором отсутствуют силы притяжения или отталкивания между молекулами и не учитывается объем молекул (молекула = мат. точка).

• 
  Закон Бойля — Мариотта: при постоянной температуре объем, занимаемый идеальным газом, изменяется обратно пропорционально его давлению: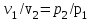
  

• 
  Закон Гей-Люссака: при постоянном давлении объемы одного и того же количества идеального газа изменяются прямо пропорционально абсолютным температурам: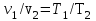
  

• 
  Закон Шарля: для данной массы газа при постоянном объеме давление прямо пропорционально температуре:
  

P₁/P₂ = T₁/T₂

2. 
   Универсальное уравнение состояния идеального газа. Универсальная газовая постоянная.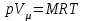
   

- уравнение Менделеева – Клайперона



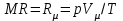Произведение M·R называют универсальной (молярной) газовой постоянной

Универсальная газовая постоянная Rm есть работа 1 моль идеального газа в процессе при постоянном давлении и при изменении температуры на 1°.

3. 
   Уравнение состояния Ван-дер-Ваальса.
   

Ван-дер-Ваальс ввел две поправки

• 
  первая поправка, зависящая от объема самих молекул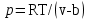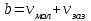
  

b – наименьший объем до которого можно сжать газ.

• 
  Вторая поправка учитывает влияние сил взаимодействия между молекулами
  

Поправка Δp прямо пропорциональна как числу притягиваемых, так и числу притягивающих молекул, или прямо пропорциональна квадрату плотности газа, или обратно пропорциональна квадрату его удельного объема: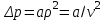



а — коэффициент пропорциональности, принимающий для каждого газа определенное числовое значение, не зависящее от параметров состояния

В итоговом виде уравнение ВДВ: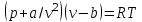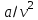



- внутреннее давление

(для воды при температуре 293 К а/v² ≈ 1080 МПа)

Возьмем уравнение ВДВ, все скобки раскроем и получим характеристическое уравнение 3-го порядка.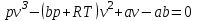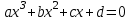





- уравнение третьей степени относительно удельного объема газа

1) все три корня различны и действительны;

2) все три корня действительны и равны между собой;

3) один корень действительный и два мнимых (комплексных) [реальное значение имеет только один действительный корень].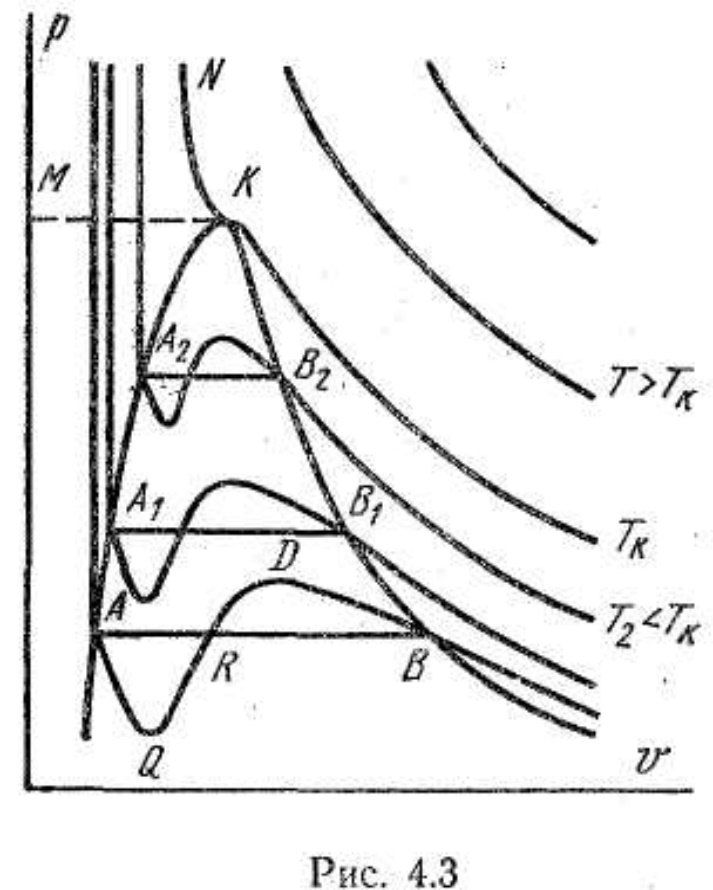

• 
  Прямая АВ, пересекающая такого типа изотерму, дает три действительных значения удельного объема в точках A, R и В, т. е. эти изотермы соответствуют первому случаю решения уравнения Ван-дер-Ваальса (три различных действительных корня).
  
• 
  При определенной температуре, называемой критической, изотерма уравнения Ван-дер-Ваальса не будет иметь волнообразного участка. На этой изотерме есть точка перегиба, касательная к которой должна быть горизонтальной. Это соответствует второму случаю решения уравнения Ван-дер-Ваальса, когда все три корня действительны и равны между собой (рис. 4.3, точка К).
  
• 
  При температурах T > T_к имеет место третий случай решения уравнения Ван-дер-Ваальса, когда один корень действительный, а два мнимых.
  

• 
  Кривую АК, на которой жидкость находится в состоянии кипения, называют пограничной кривой жидкости (нижней пограничной кривой);
  
• 
  криваяВК, называемая пограничной кривой пара (верхней пограничной кривой), представляет собой совокупность состояний сухого насыщенного пара.
  

Таким образом, для реального вещества рv-диаграмму можно разбить на три характерные области:

1) область жидкого состояния, расположенную левее пограничной кривой жидкости;

2) область двухфазных состояний (влажного пара), расположенную между пограничными кривыми жидкости и пара;

3) область перегретого пара, расположенную правее пограничной кривой пара и выше критической точки.

4. 
   Критические параметры вещества.
   

Критические точки – это точки соответствующие температуре, при которой пропадает различие между жидкостью и газом, поверхностное натяжение воды становится = 0.

Критические параметры, выраженные через константы уравнения a и b: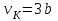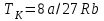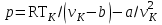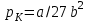







Константы а и b при известных критических параметрах: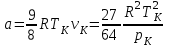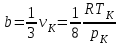

5. 
   Общее аналитическое выражение первого закона термодинамики.
   

Сумма изменений внутренней кинетической и внутренней потенциальной энергии представляет полное изменение удельной внутренней энергии du.

С увеличением объема на dv тело совершает внешнюю работу по преодолению внешних сил, которую обозначают δl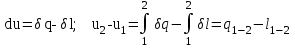



Математическое выражение первого закона термодинамики :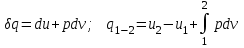



изменение удельной внутренней энергии термодинамической системы равно алгебраической сумме полученной системой энергии в форме удельной теплоты δq и совершенной ею внешней удельной работой δl,

или подведенная к рабочему телу энергия в форме удельной теплоты расходуется на изменение удельной внутренней энергии тела и на совершение телом внешней работы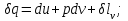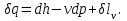





Уравнения (написанные выше) являются наиболее общим аналитическим выражением первого закона термодинамики для обратимых процессов изменения состояния термодинамической системы.

6. 
   Истинная и средняя теплоемкости. Отношение теплоемкостей ср и сv.
   

Истинной теплоемкостью называется отношение элементарного количества теплоты, сообщаемой термодинамической системе в каком-либо процессе, к бесконечно малой разности температур.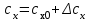



Первое слагаемое c_x0представляет собой теплоемкость данного газа в разреженном (идеально газовом) состоянии (при p→0 или v→∞) и зависит только от температуры.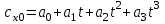



Второе слагаемое Δс_х определяет зависимость теплоемкости от давления или удельного объема и связано с изменением потенциальной составляющей внутренней энергии реального газа.

Средней теплоемкостью данного процесса в интервале температур от t₁ до t₂ называют отношение количества теплоты q_1-2 к конечной разности температур t₂ — t₁: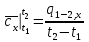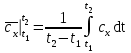





Отношение теплоемкости при постоянном давлении к теплоемкости при постоянном объеме, обозначаемое обычно k: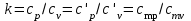



Величина k определяется числом степеней свободы молекулы.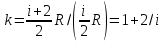



для одноатомного газа k = 1,66;

для двухатомного газа k = 1,4;

для трех- и многоатомных газов k = 1,33.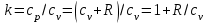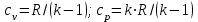

7. 
   Общие вопросы исследования термодинамических процессов идеальных газов.
   

К основным процессам относятся:

• 
  изохорный, протекающий при постоянном объеме v = const;
  
• 
  изобарный, протекающий при постоянном давлении p = const;
  
• 
  изотермический, протекающий при постоянной температуре T = const;
  
• 
  адиабатный, протекающий при отсутствии теплообмена с внешней средой S = const;
  
• 
  политропные, характеризующиеся постоянством теплоемкости в процессе c_x = const.
  

Общий метод исследований процессов

1. 
   Выводится уравнение кривой процесса на pv- и Ts-диаграммах;
   
2. 
   Устанавливается зависимость между основными параметрами рабочего тела в начале и конце процесса;
   
3. 
   Определяется изменение удельной внутренней энергии по формуле, справедливой для всех процессов идеального газа: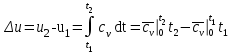
   

или при постоянной теплоемкости: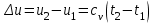



4. Вычисляется работа изменения объема газа по основной формуле: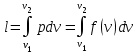



5. Определяется удельное количество теплоты, участвующее в процессе, по формуле: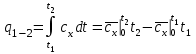



6. Определяется изменение удельной энтальпии в процессе по формуле, справедливой для всех процессов идеального газа: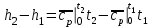



или для постоянной теплоемкости: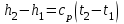



7. Определяется изменение удельной энтропии идеального газа по формулам: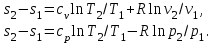



Рассматриваемые процессы считаются обратимыми.

8. 
   Прямой обратимый цикл Карно.
   

Обратимый цикл, осуществленный между двумя источниками теплоты постоянной температуры, состоящий из двух обратимых изотермических и двух обратимых адиабатных процессов, называется циклом КАРНО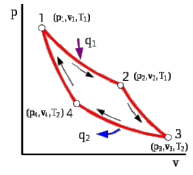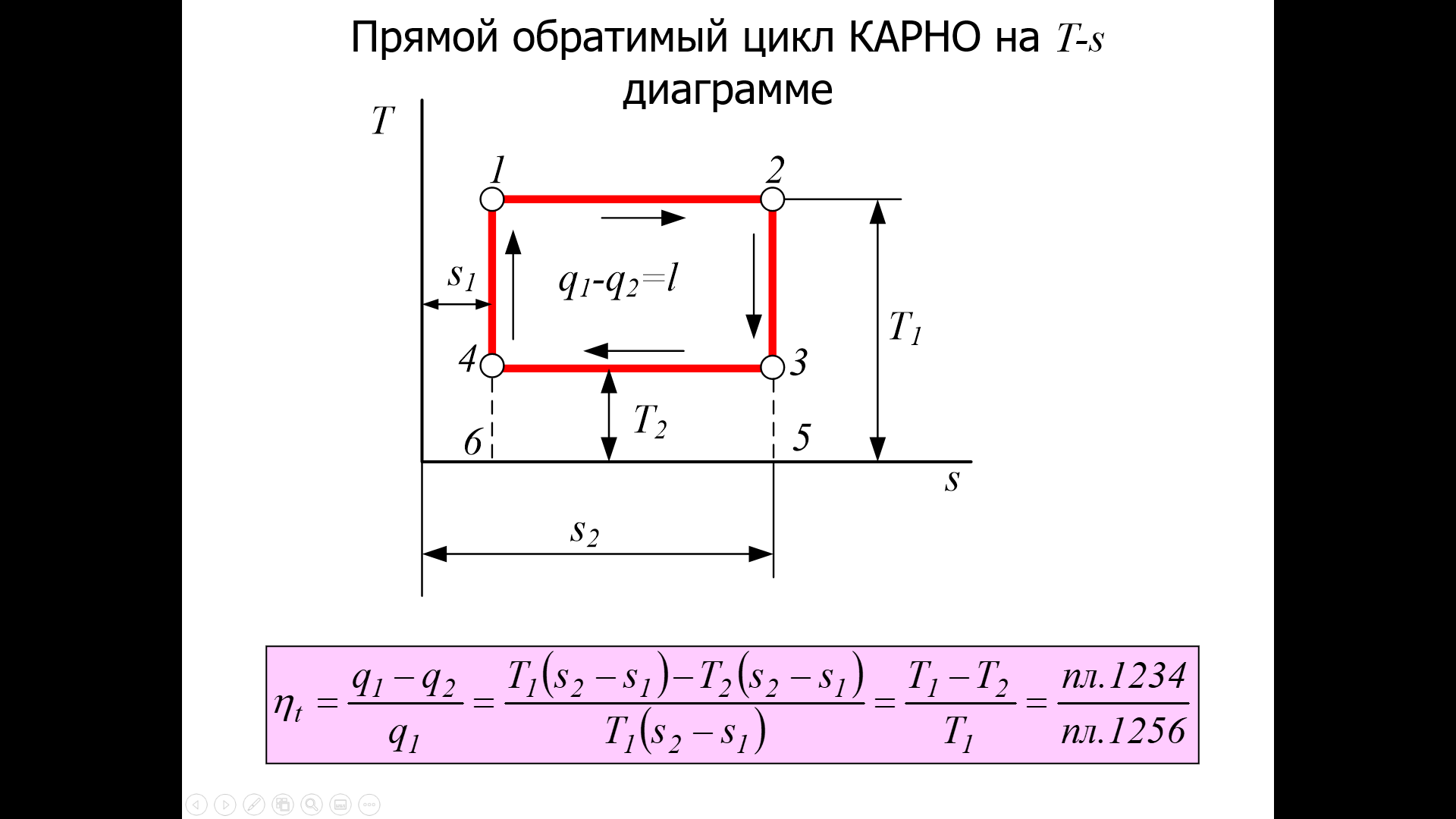

9. 
   Обратный обратимый цикл Карно.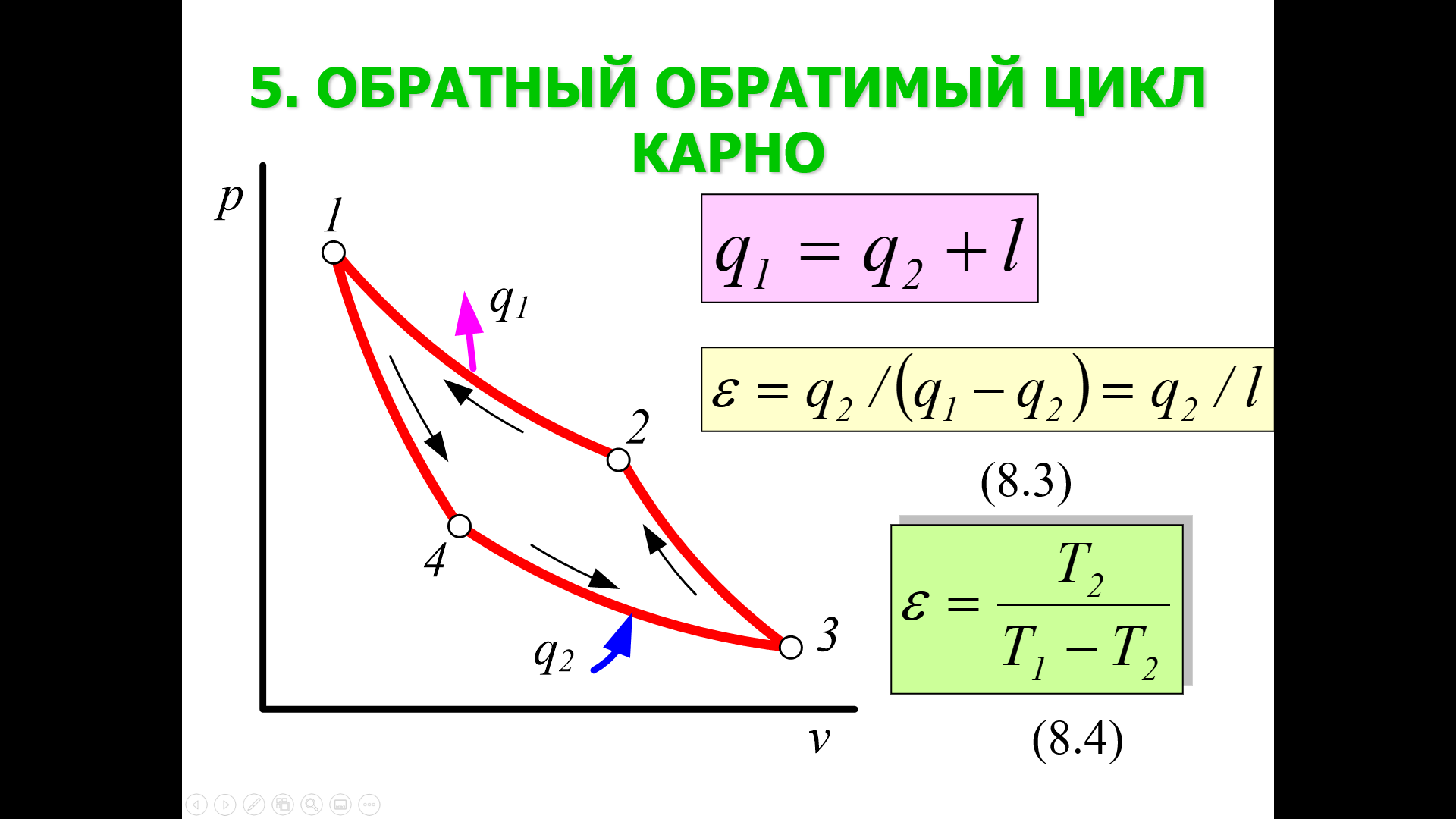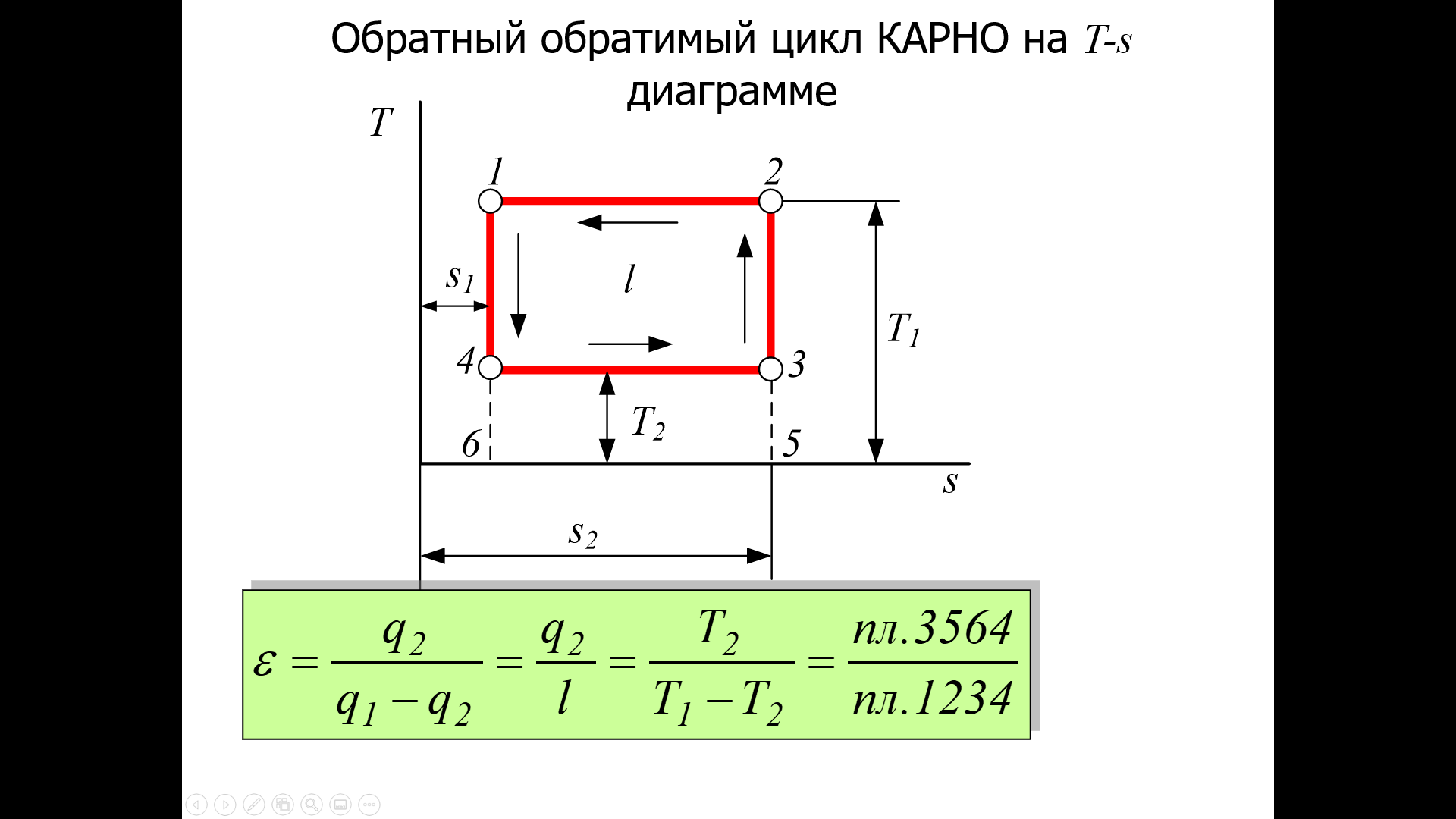
   

Машина, работающая по обратному циклу, называется холодильной машиной

Затрачиваемая внешняя работа сжатия больше работы расширения на величину пл. ₁₄₃₂ внутри замкнутой линии цикла. Эта работа превращается в теплоту и передается вместе с теплотой q₂ источнику с температурой Т₁. Таким образом, затратив на осуществление обратного цикла удельную работу l, можно перенести от теплоприемника к теплоотдатчику q₂ единиц теплоты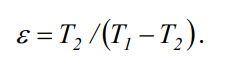



Из рассмотрения обратного цикла Карно можно сделать вывод, что передача теплоты от источника с низкой температурой к источнику с высокой температурой, как это следует из постулата Клаузиуса, обязательно требует затраты энергии.

10. 
    Обобщенный (регенеративный) цикл Карно.
    

11. 
    Располагаемая работа при истечении газа. Скорость истечения и массовый расход идеального газа из суживающегося сопла.
    

Величина dw2 /2, равная бесконечно малому приращению внешней кинетической энергии рабочего тела, называется элементарной располагаемой работой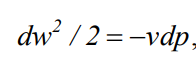



Массовый расход идеального газа зависит от площади выходного сечения канала, начального состояния газа и степени его расширения

Массовый расход: m = a*w/v

а – площадь поперечного сечения канала,

w – скорость газа,

V₂ – удельный объём в выходном сечении сопла.

Скорость истечения газа зависит от состояния газа при входе в сопло и от давления р2 на выходе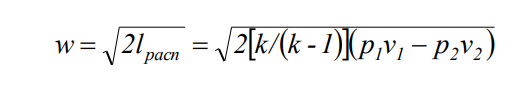

12. 
    Случаи истечения идеального газа из сужающегося сопла
    

Первый случай

Давление внешней среды больше критического. При этих условиях используется весь перепад давления и происходит полное расширение газа. Скорость газа в выходном сечении сопла меньше скорости звука. Давление газа в выходном сечении сопла равно давлению внешней среды

Второй случай

Давление внешней среды меньше критического. При этих условиях используется не весь перепад давлений, а только часть от р1 до рк, происходит неполное расширение газа, и скорость газа в выходном сечении суживающегося сопла равна критической скорости или местной скорости звука). Давление в устье сопла равно критическому давлению:

p_к  p₁_к