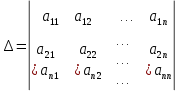Закон Кулона для взаимодействия точечных зарядов или заряженных шариков в вакууме записывается в форме, (1) где электрическая постоянная в си
 Скачать 23.93 Kb. Скачать 23.93 Kb.
|
|
Задание 1 Закон Кулона для взаимодействия точечных зарядов или заряженных шариков в вакууме записывается в форме
где  - электрическая постоянная в СИ. - электрическая постоянная в СИ.Каждый электрический заряд создает в пространстве электрическое поле независимо от наличия других электрических зарядов. Принцип наложения (суперпозиции) электрических полей: напряженность электрического поля системы N зарядов равна векторнойсумме напряженностей полей, создаваемых каждым из них в отдельности:
где N – произвольное положительное число. Абсолютная величина  действительного числаaпо определению есть действительного числаaпо определению есть число, равное a, если a  0, или равное 0, или равное 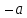 , если aменьше 0. , если aменьше 0.Отметим
  
Задание 2 1. Элементарные примеры раскрытия неопределенностей разного вида. Предел отношения двух многочленов с постоянными коэффициентами. Пусть  . .При х 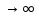 отношение многочленов представляет неопределенность вида отношение многочленов представляет неопределенность вида  . Для ее раскрытия преобразуем каждый многочлен, вынося за скобки переменную в наибольшей степени: . Для ее раскрытия преобразуем каждый многочлен, вынося за скобки переменную в наибольшей степени:
Таким образом, можно сформулировать следующие правила: Предел отношения двух многочленов одинаковой степени равен отношению коэффициентов при старшей степени; Если степень многочлена, стоящего в числителе, больше степени многочлена, стоящего в знаменателе, то предел их отношения равен бесконечности; Если степень многочлена, стоящего в знаменателе, выше степени многочлена, стоящего в числителе, то предел их отношения равен нулю. 2. Найти наибольшее значение функции  в интервале (0; в интервале (0; ). Решение. ). Решение.Всюду в интервале (0;  ) функция дифференцируема. Найдем ) функция дифференцируема. Найдем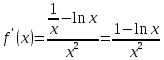 . Так как . Так как  при при  , то x=e. , то x=e.Задание 3. Метод Крамера решения системы  линейных уравнений с линейных уравнений с  неизвестными. неизвестными.Рассмотрим систему  алгебраических линейных уравнений с алгебраических линейных уравнений с  неизвестными: неизвестными:
Определителем системы называется определитель матрицы системы
  Обозначим Обозначим  - определитель, который получится из определителя системы - определитель, который получится из определителя системы  заменой j-го столбца на столбец заменой j-го столбца на столбец 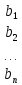 . . |

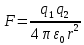 ,
, ,
, ; из
; из  ,
,
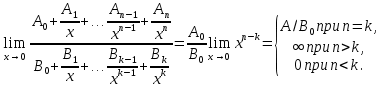

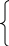 ;
;