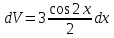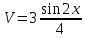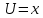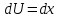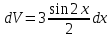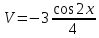математика. Математика Зарипова. Математика
 Скачать 160.8 Kb. Скачать 160.8 Kb.
|
ВЫПОЛНЕНИЕ ПРАКТИЧЕСКИХ ЗАДАНИЙ ПО ДИСЦИПЛИНЕ МатематикаГруппа Пм21М571в Студент Зарипова М.В. МОСКВА 2021 Выполнить деление комплексных чисел 1.1 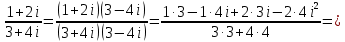 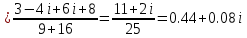 1.2 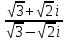 = =  = = 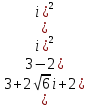 = = = =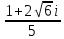 Вычислить пределы последовательностей 2.1. 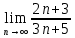 Ведущим членом в знаменателе 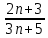 является n. Нужно разделить числитель и знаменатель так: является n. Нужно разделить числитель и знаменатель так: 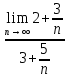 Выражения 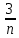 и и 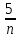 стремятся к нулю при приближении n к бесконечности, поэтому ответ такой: стремятся к нулю при приближении n к бесконечности, поэтому ответ такой: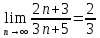 2.2. 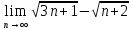 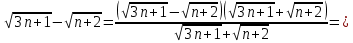 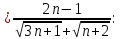 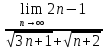  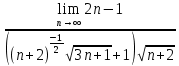 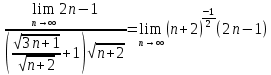 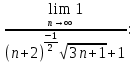 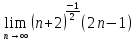 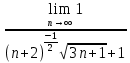 Используем взаимное правило: 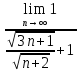 в виде в виде 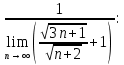 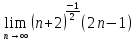 в виде в виде 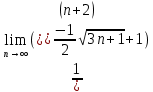 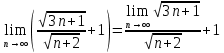 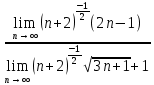 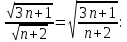 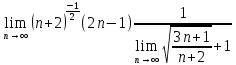 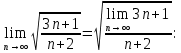 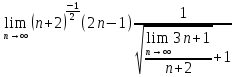 Ведущим членом в знаменателе 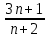 является n. Нужно разделить числитель и знаменатель так: является n. Нужно разделить числитель и знаменатель так: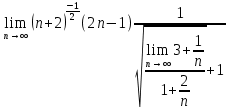 Выражения  и и 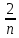 стремятся к нулю при приближении n к бесконечности поэтому: стремятся к нулю при приближении n к бесконечности поэтому: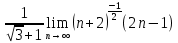 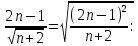 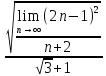 Выражение 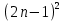 растёт асимптотически быстрее чем n+2 так как n приближается к бесконечности растёт асимптотически быстрее чем n+2 так как n приближается к бесконечности Кроме того 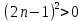 и n+2>0 так как n приближается к бесконечности и n+2>0 так как n приближается к бесконечностиИ так:  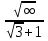 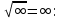 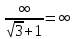 Ответ: 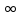 3. Используя признаки Даламбера и Коши исследовать сходимость рядов 3.1  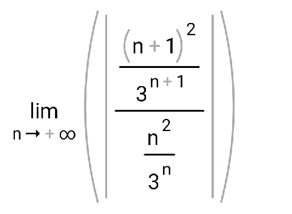 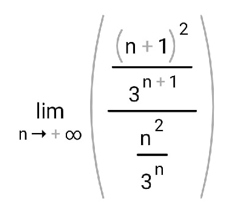 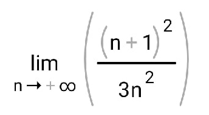   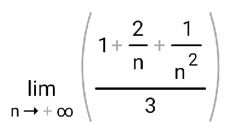  Ответ:_Ряд_сходится'>Ответ: Ряд сходится 3.2 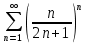 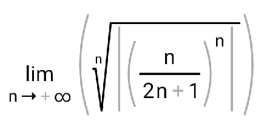 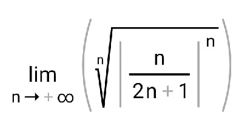 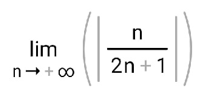 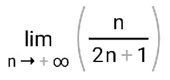 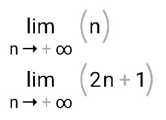 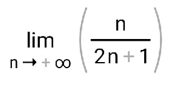 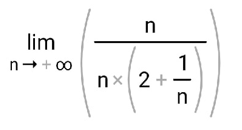 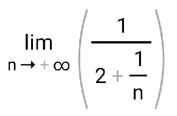  Ответ: Ряд сходится 4. Найти производные сложных функций 4.1. 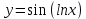 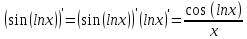 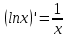 Ответ: 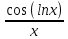 4.2. 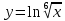 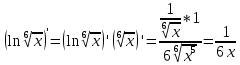 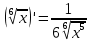 Поскольку: 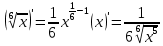 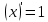 Ответ: 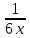 5. Вычислить неопределенный интеграл 5.1. 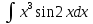 Формула интегрирования по частям: 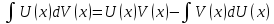 Положим 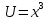 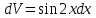 Тогда:  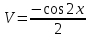 Поэтому: 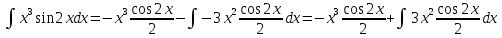 Находим интеграл 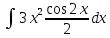
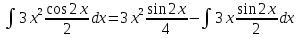 Находим интеграл 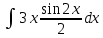
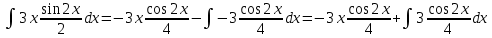 Находим интеграл 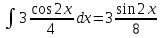 Ответ: 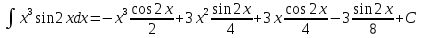 5.2. 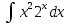 Формула интегрирования по частям: 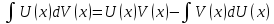 Положим  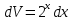 Тогда: 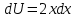 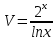 Поэтому: 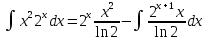 Находим интеграл 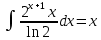 Ответ:  6. Найти частные производные первого и второго порядка 6.1   = = ’ = ’ =   = =   ( ( 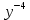 )’= )’=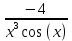  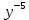  = = 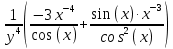 ‘ = ‘ =   = =     = =  6.2  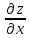 = =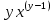 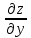 =lnx =lnx 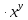  = =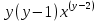 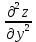 = (lnx = (lnx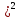 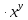  = = +ylnx +ylnx  Найти сумму матриц 7.1  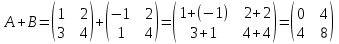 7.2 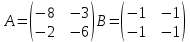 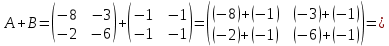 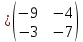 Найти произведение матриц 8.1 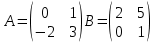 Компоненты матрицы С вычисляются следующим образом:  = =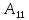 · ·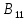 + +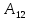 · ·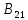 =0 2+1 0=0+0=0 =0 2+1 0=0+0=0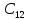 = =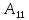 · ·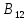 + +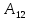 · · =0 5+1 1=0+1=1 =0 5+1 1=0+1=1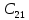 = = · ·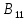 + +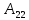 · ·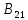 =(-2) 2+3 0=(-4)+0=-4 =(-2) 2+3 0=(-4)+0=-4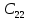 = = · ·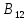 + +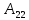 · · =(-2) 5+3 1=(-10)+3=-7 =(-2) 5+3 1=(-10)+3=-7Ответ: 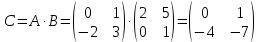 8.2 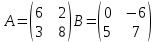 Компоненты матрицы С вычисляются следующим образом:  = =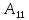 · ·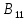 + +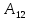 · ·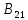 =6 0+2 5=0+10=10 =6 0+2 5=0+10=10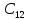 = =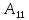 · ·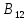 + +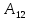 · · =6 (-6)+2 7=(-36)+14=-22 =6 (-6)+2 7=(-36)+14=-22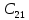 = = · ·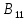 + +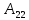 · ·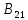 =3 0+8 5=0+40=40 =3 0+8 5=0+40=40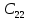 = = · ·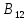 + +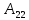 · · =3 (-6)+8 7=(-18)+56=38 =3 (-6)+8 7=(-18)+56=38Ответ: 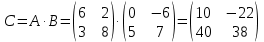 Найти определители матриц 9.1 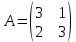 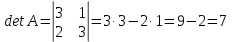 9.2 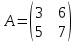  Решить систему уравнений 10.1 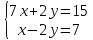 Решим данную систему уравнений методом Крамера Приведём систему уравнений к каноническому виду 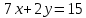 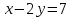 Запишем систему линейных уравнений в матричном виде 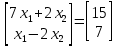 Это есть система уравнений, имеющая форму 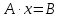 Так как определитель матрицы 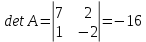 То корень 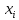 получается делением определителя матрицы получается делением определителя матрицы 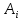 на определитель матрицы на определитель матрицы 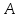 . ( . (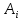 получаем заменой в матрице получаем заменой в матрице 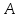 i-го столбца на столбец i-го столбца на столбец 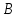 ) )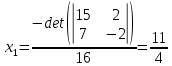 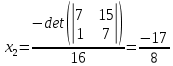 10.2 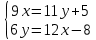 Решим данную систему уравнений методом Крамера Приведём систему уравнений к каноническому виду 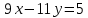 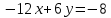 Запишем систему линейных уравнений в матричном виде 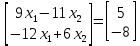 Это есть система уравнений, имеющая форму 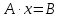 Так как определитель матрицы  То корень 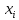 получается делением определителя матрицы получается делением определителя матрицы 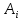 на определитель матрицы на определитель матрицы 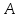 . ( . (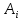 получаем заменой в матрице получаем заменой в матрице 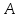 i-го столбца на столбец i-го столбца на столбец 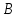 ) )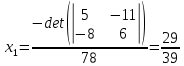 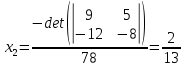 Для заданных векторов найти смешанное произведение 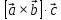 11.1 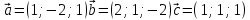 Запишем матрицу в виде  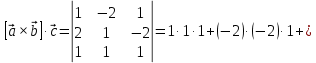 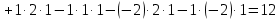 11.2  Запишем матрицу в виде 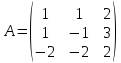 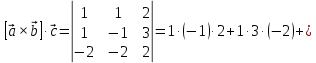 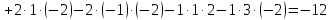 |