1. Электрический заряд. Закон Кулона
 - закон Кулона. - закон Кулона.
2. Напряженность поля. Теорема Гаусса
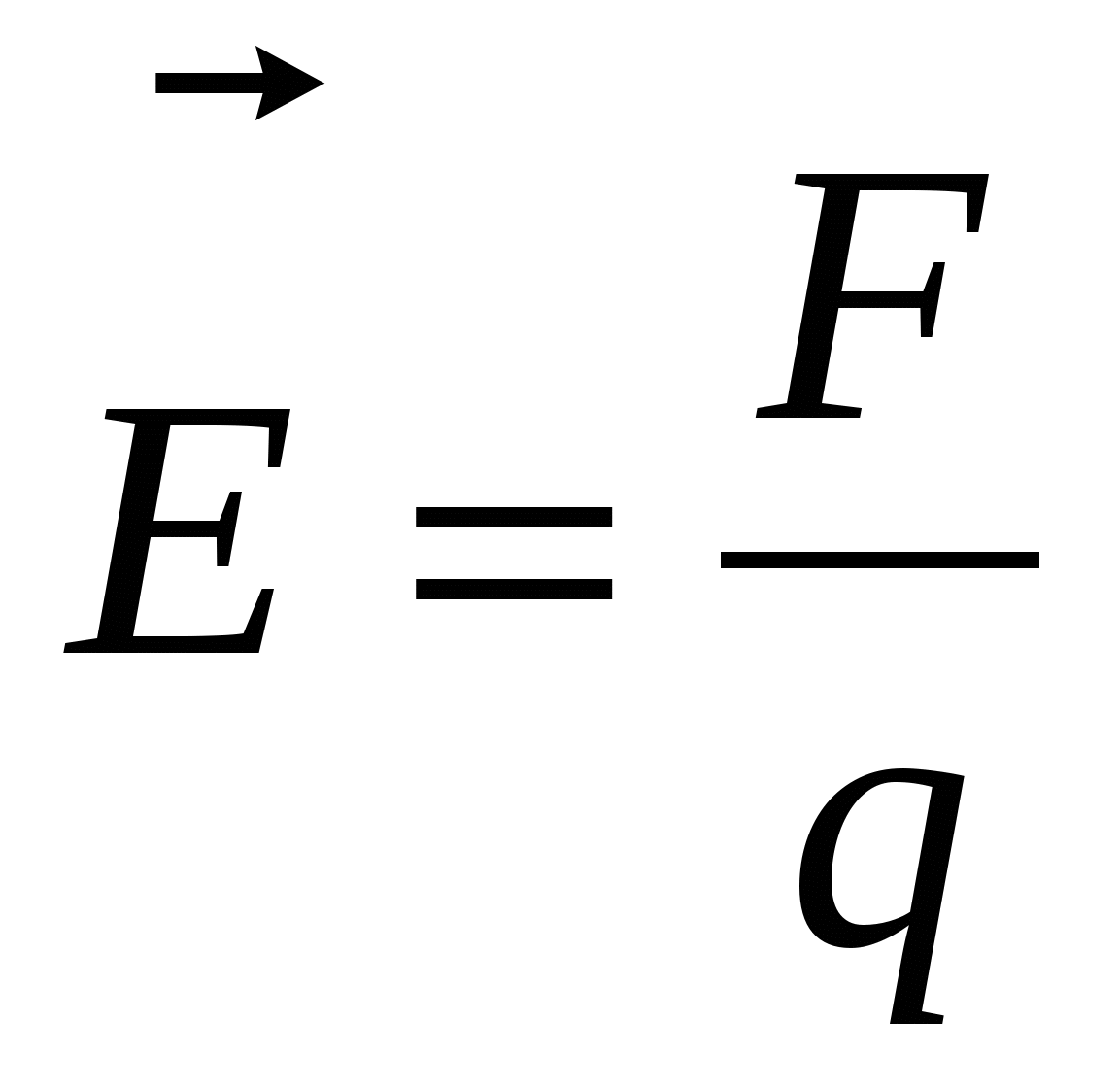 - определение напряженности поля; - определение напряженности поля;
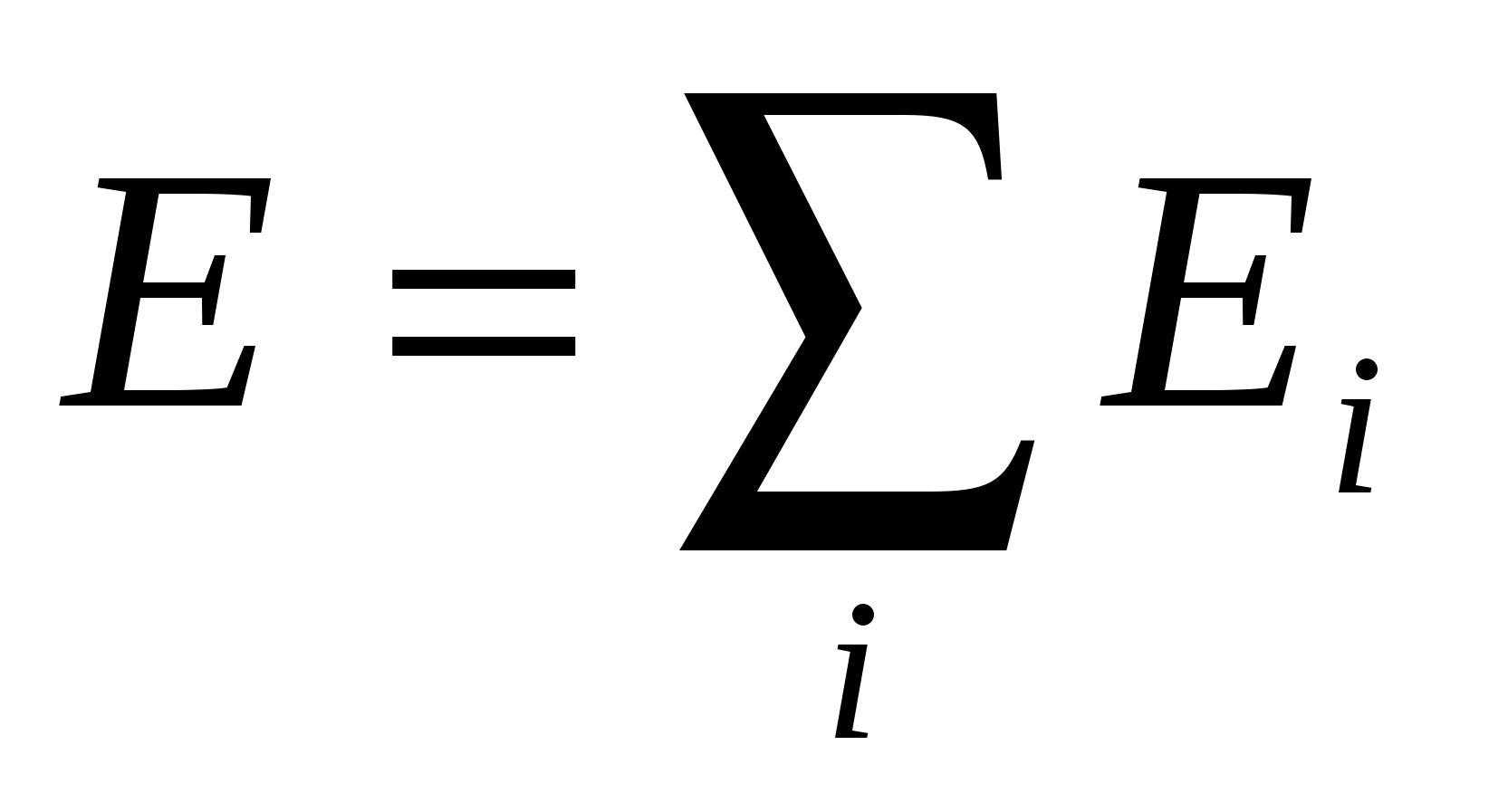 , , 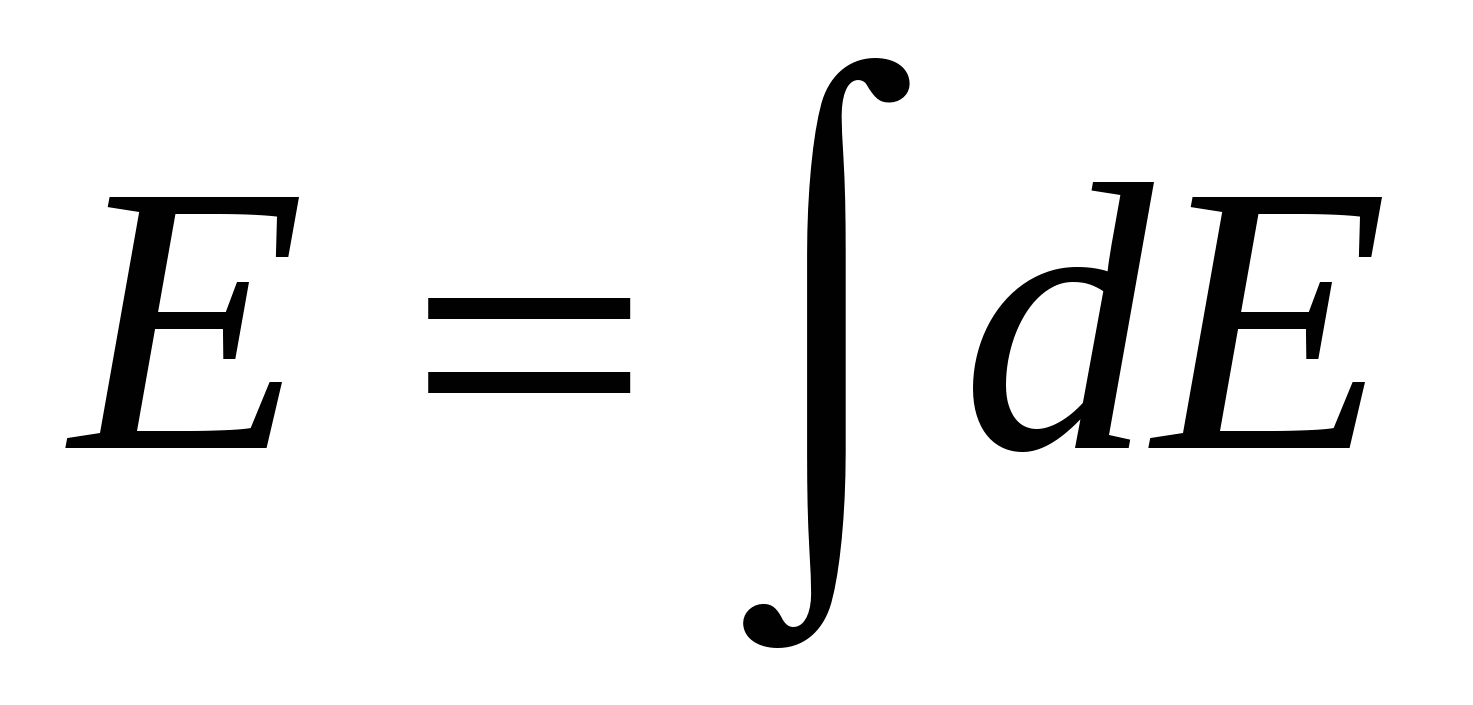 - принцип суперпозиции; - принцип суперпозиции;
 - диэлектрическая проницаемость диэлектрика; - диэлектрическая проницаемость диэлектрика;
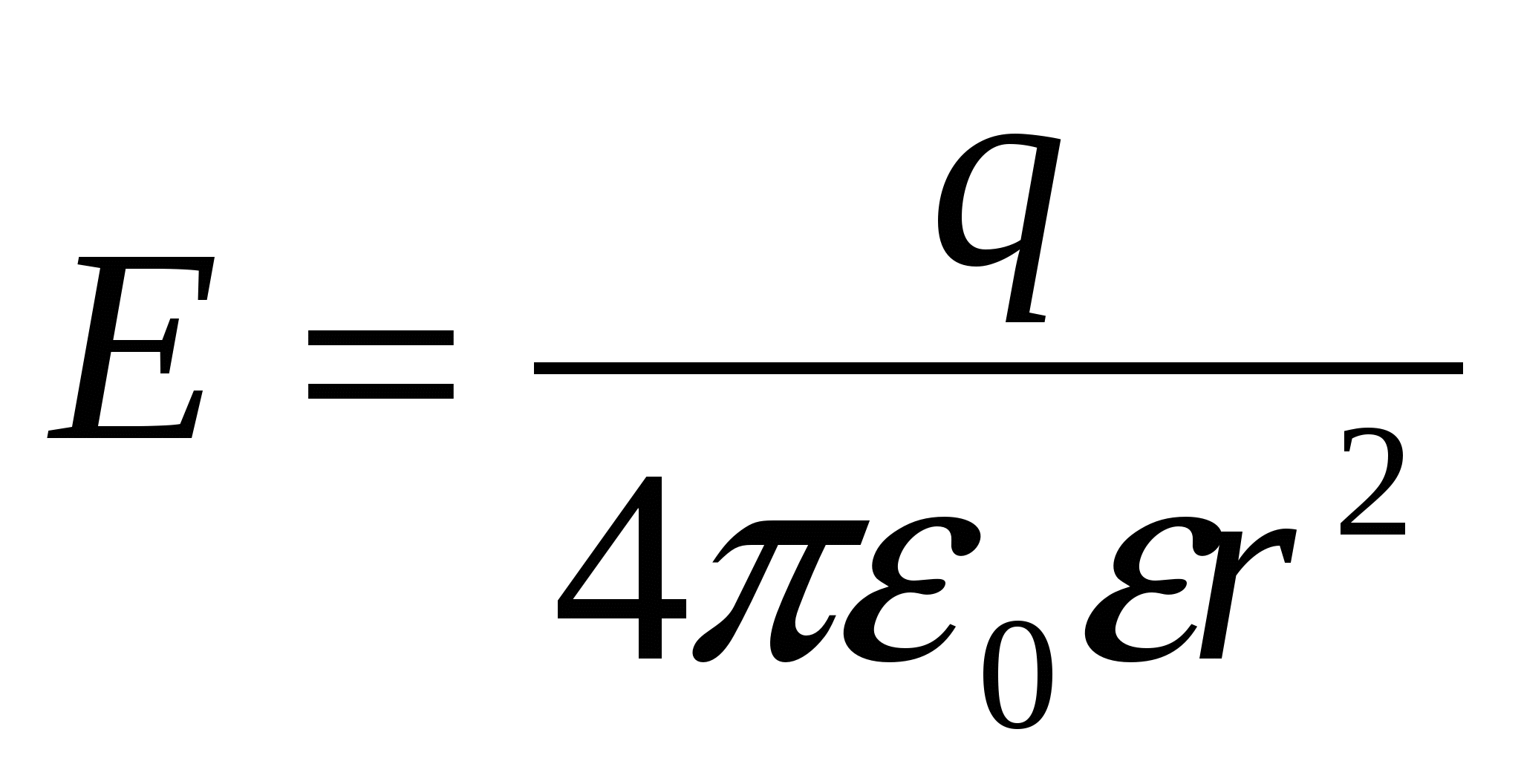 - напряженность поля точечного заряда; - напряженность поля точечного заряда;
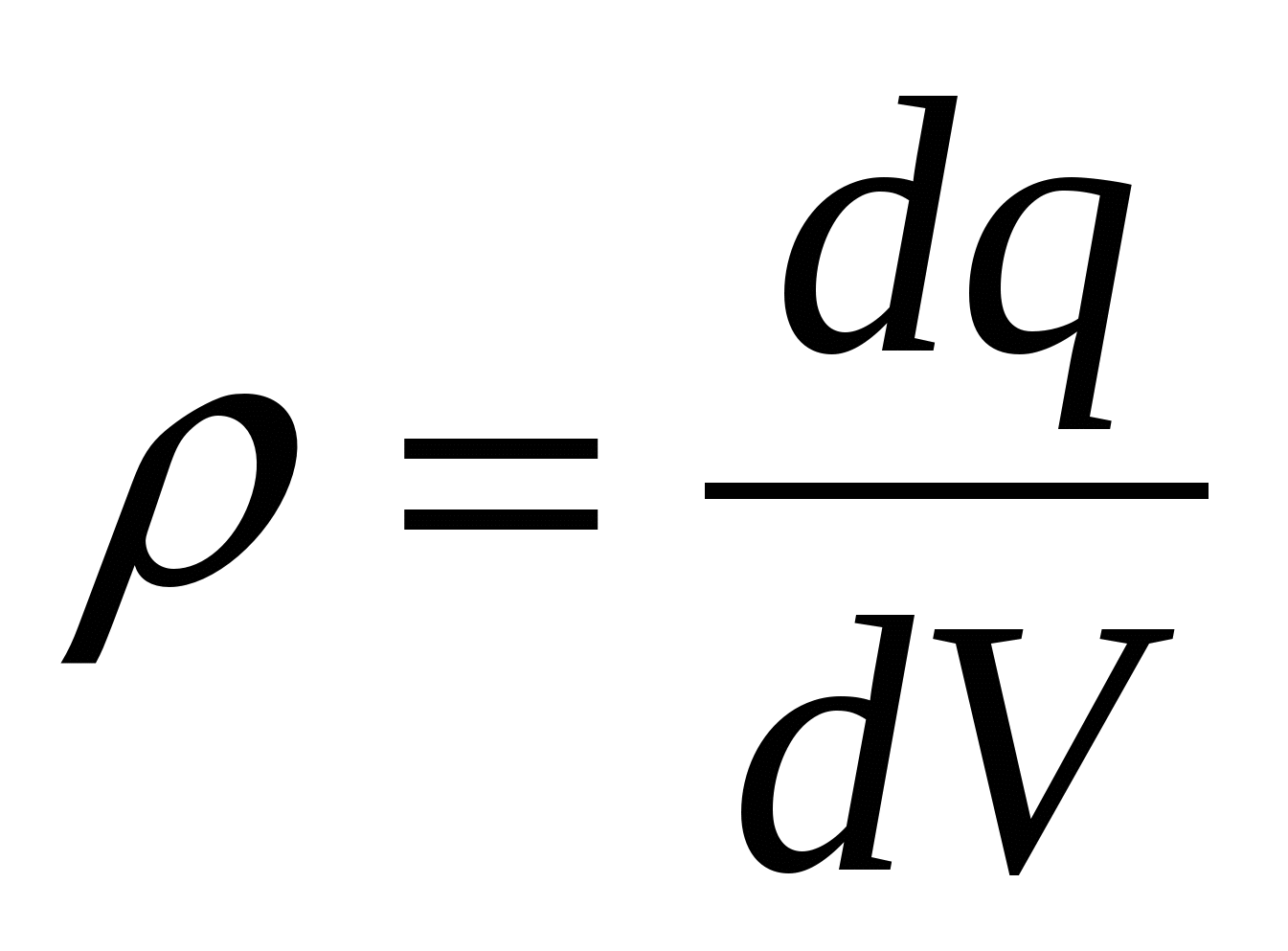 , , 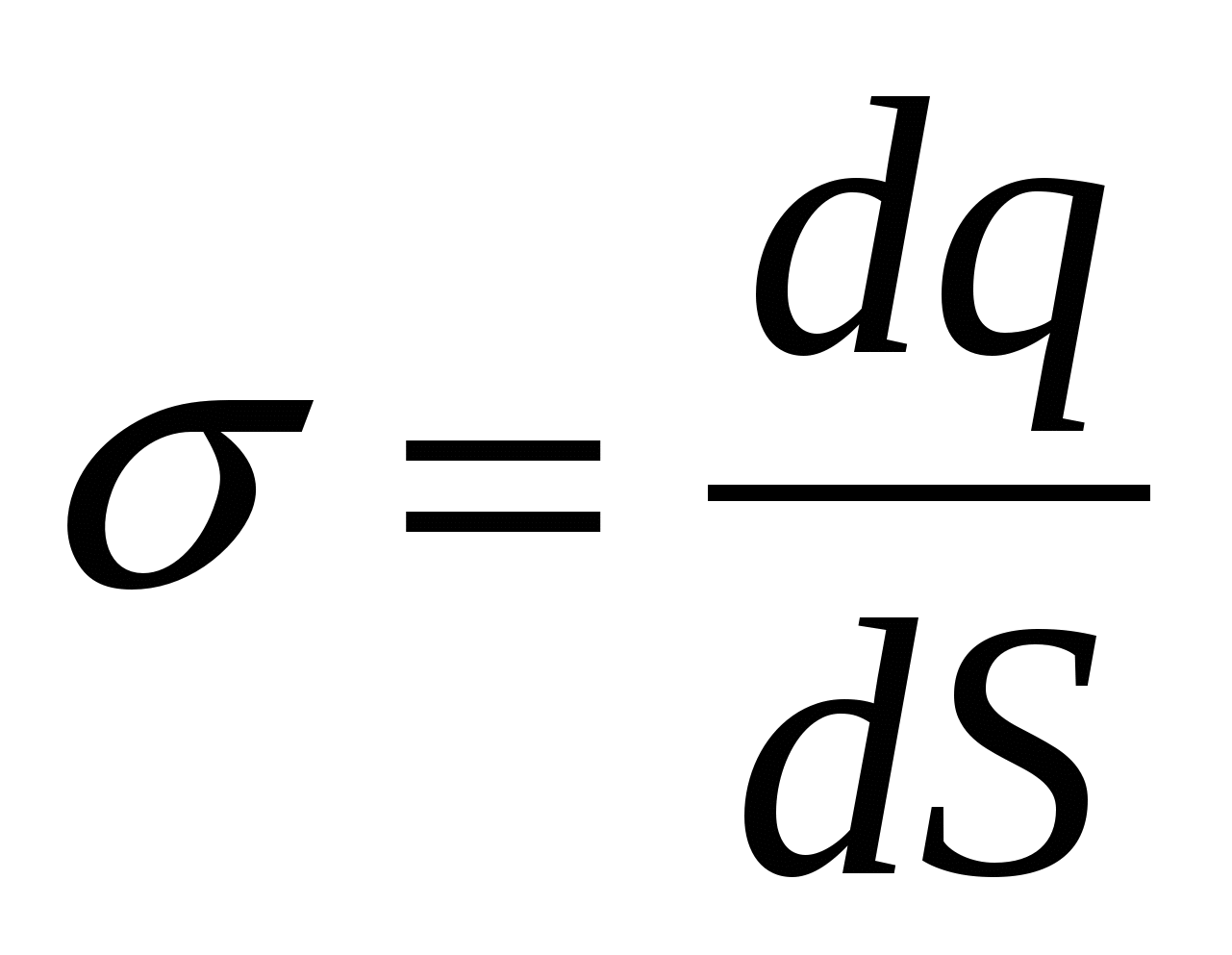 , ,  - объемная, поверхностная, линейная плотности заряда; - объемная, поверхностная, линейная плотности заряда;
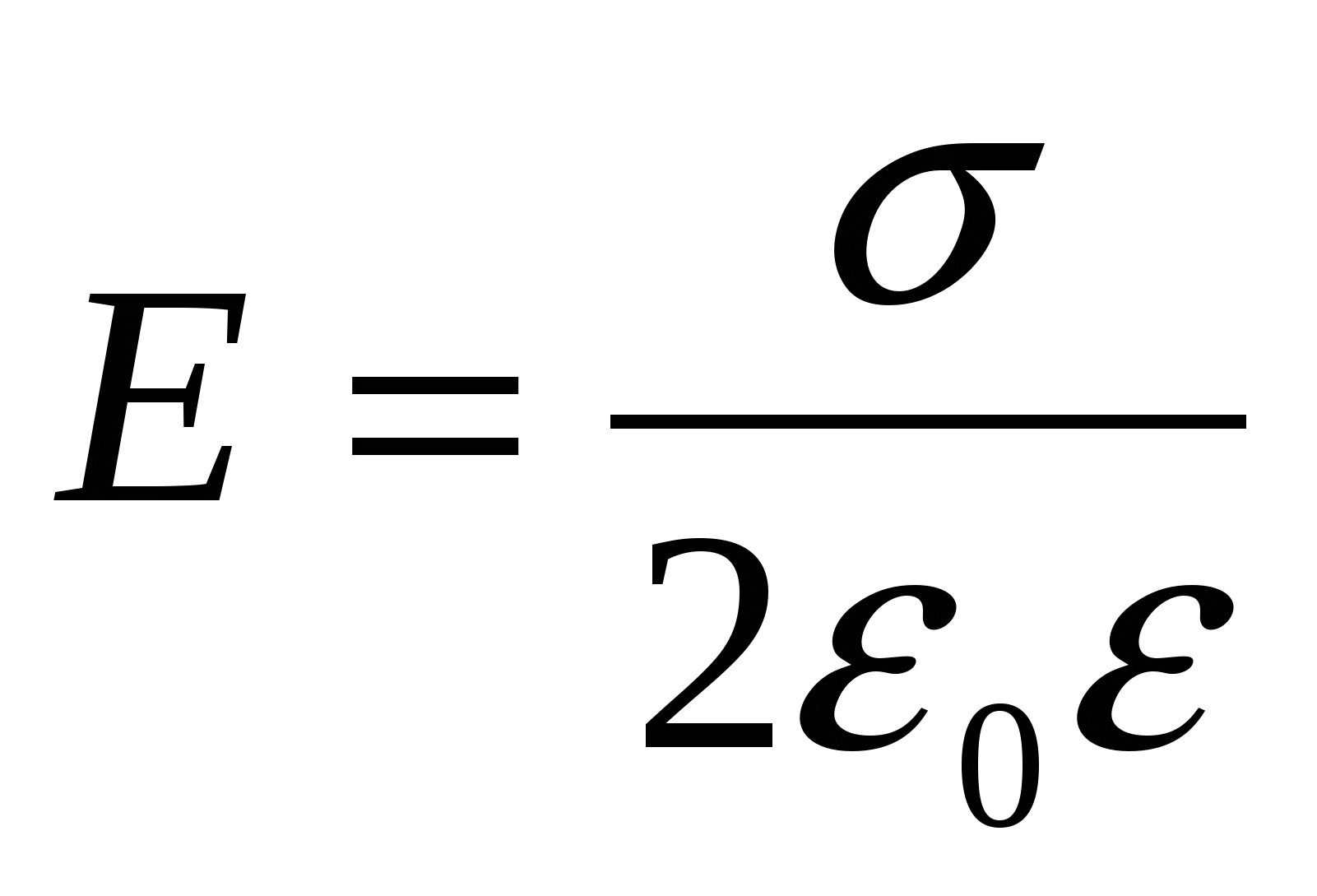 - напряженность поля плоскости; - напряженность поля плоскости;
 - напряженность поля конденсатора; - напряженность поля конденсатора;
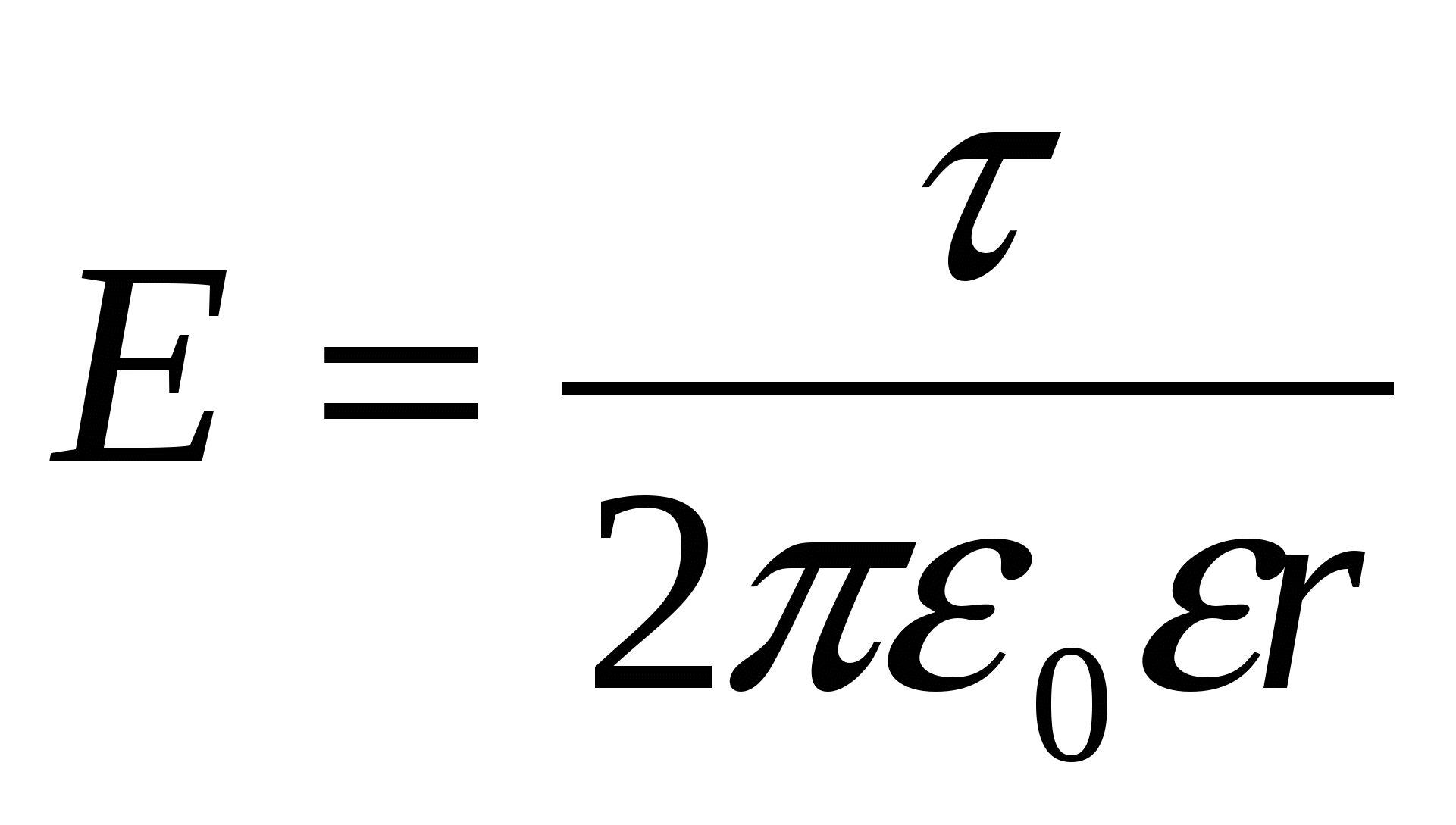 - напряженность поля нити (цилиндра при r>R, R – радиус цилиндра); - напряженность поля нити (цилиндра при r>R, R – радиус цилиндра);
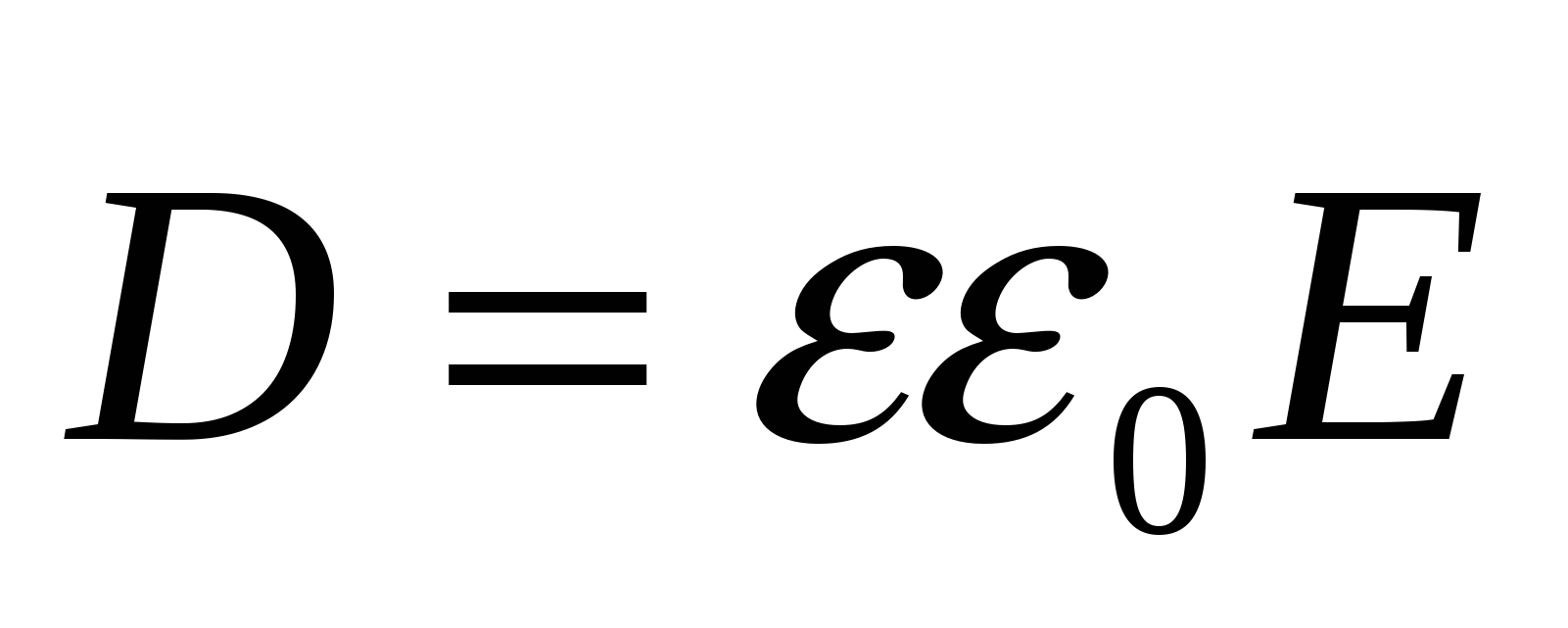 - вектор электрического смещения; - вектор электрического смещения;
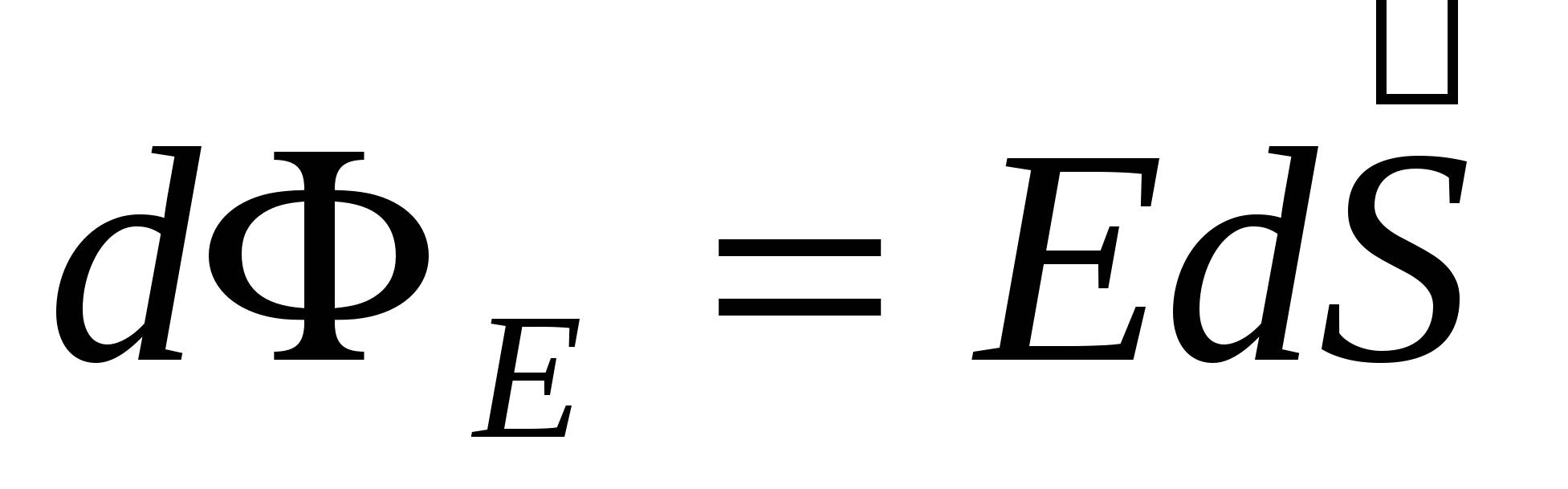 , ,  - поток вектора напряженности; - поток вектора напряженности;
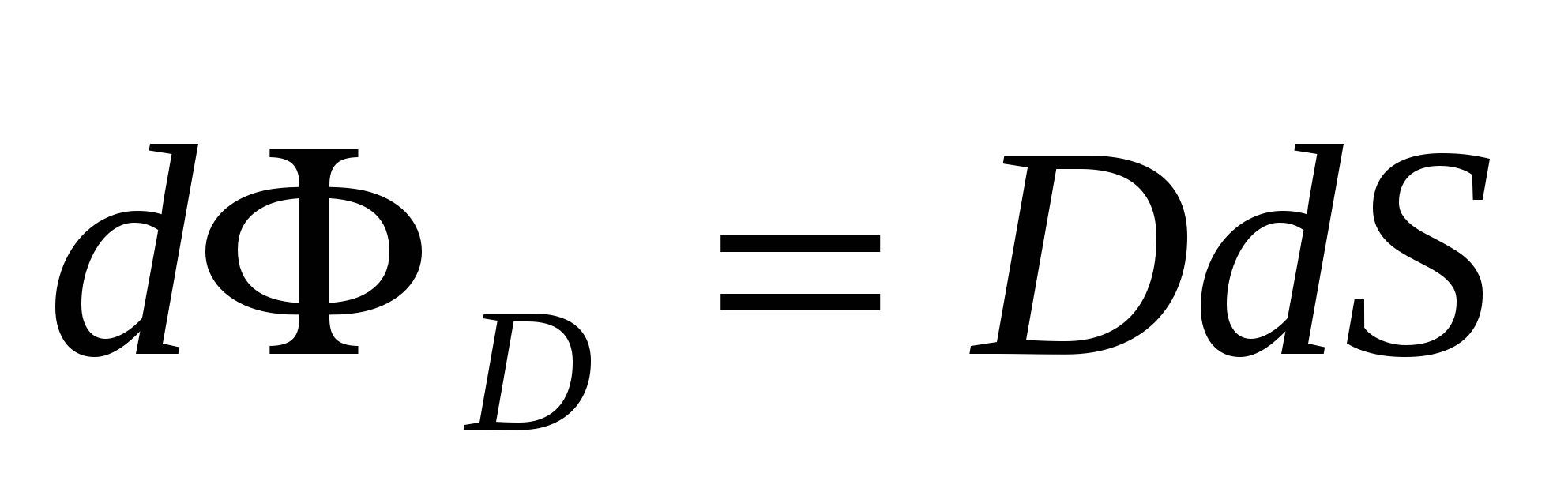 , ,  - поток вектора электрического смещения; - поток вектора электрического смещения;
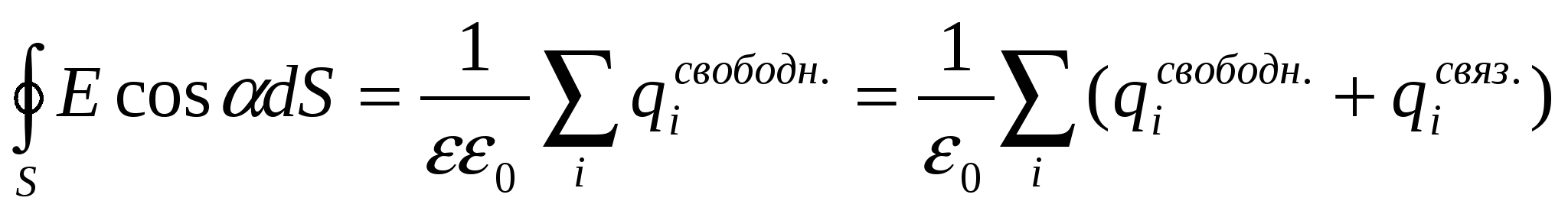 , , 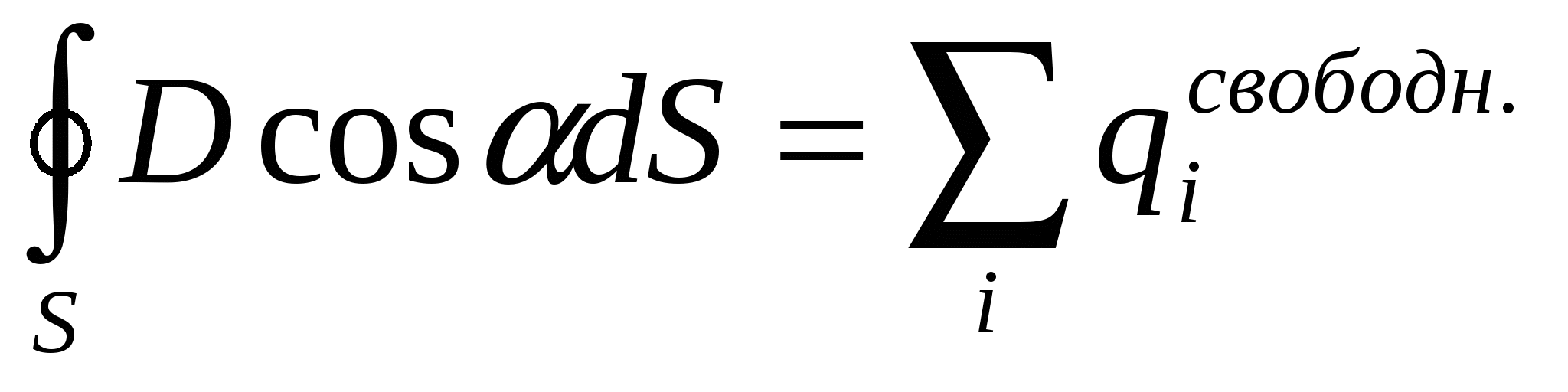 - теорема Гаусса. - теорема Гаусса.
3.Энергия взаимодействия точечных зарядов. Потенциал
 - энергия взаимодействия точечных зарядов; - энергия взаимодействия точечных зарядов;
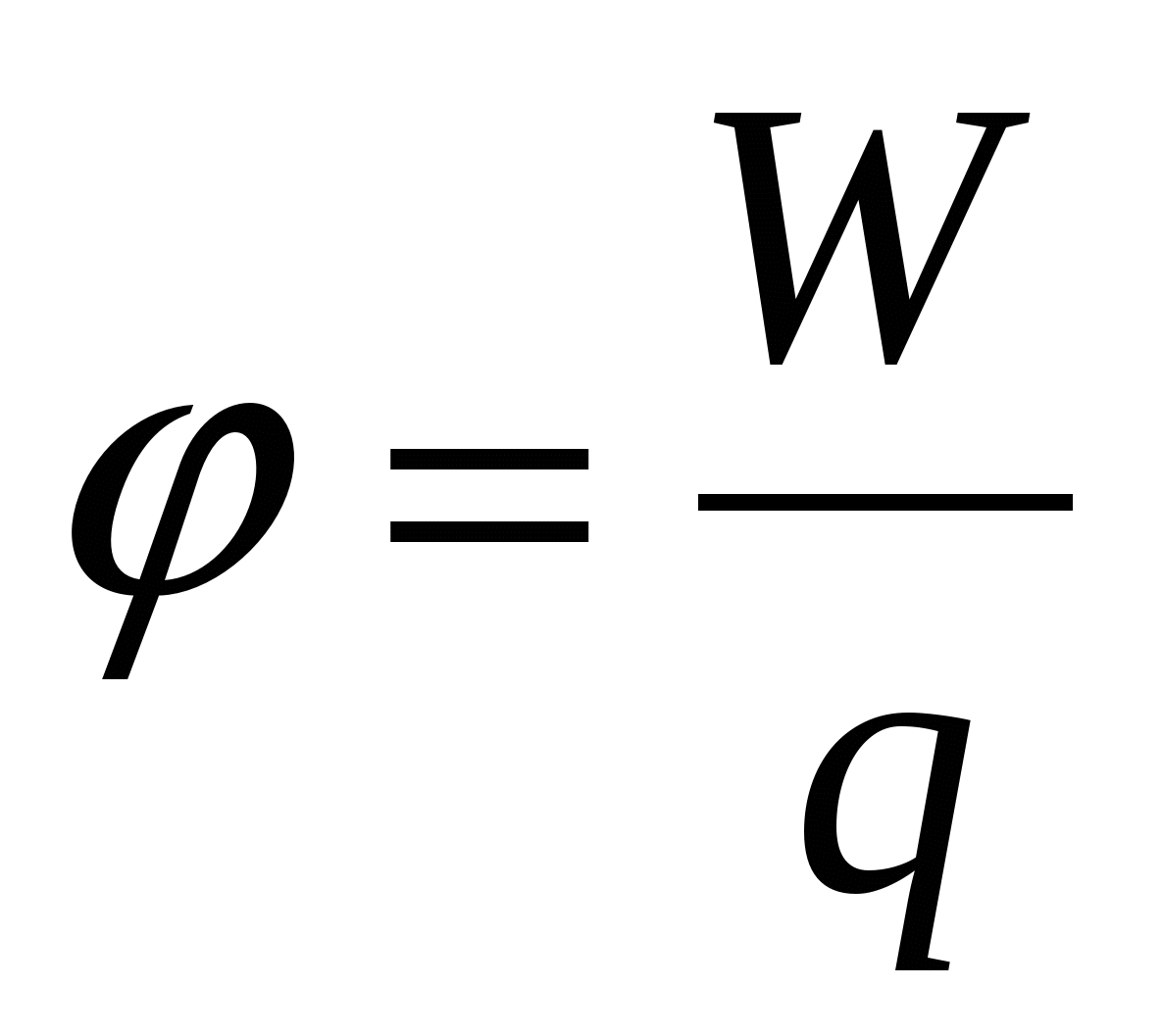 - определение потенциала; - определение потенциала;
 - потенциал поля точечного заряда; - потенциал поля точечного заряда;
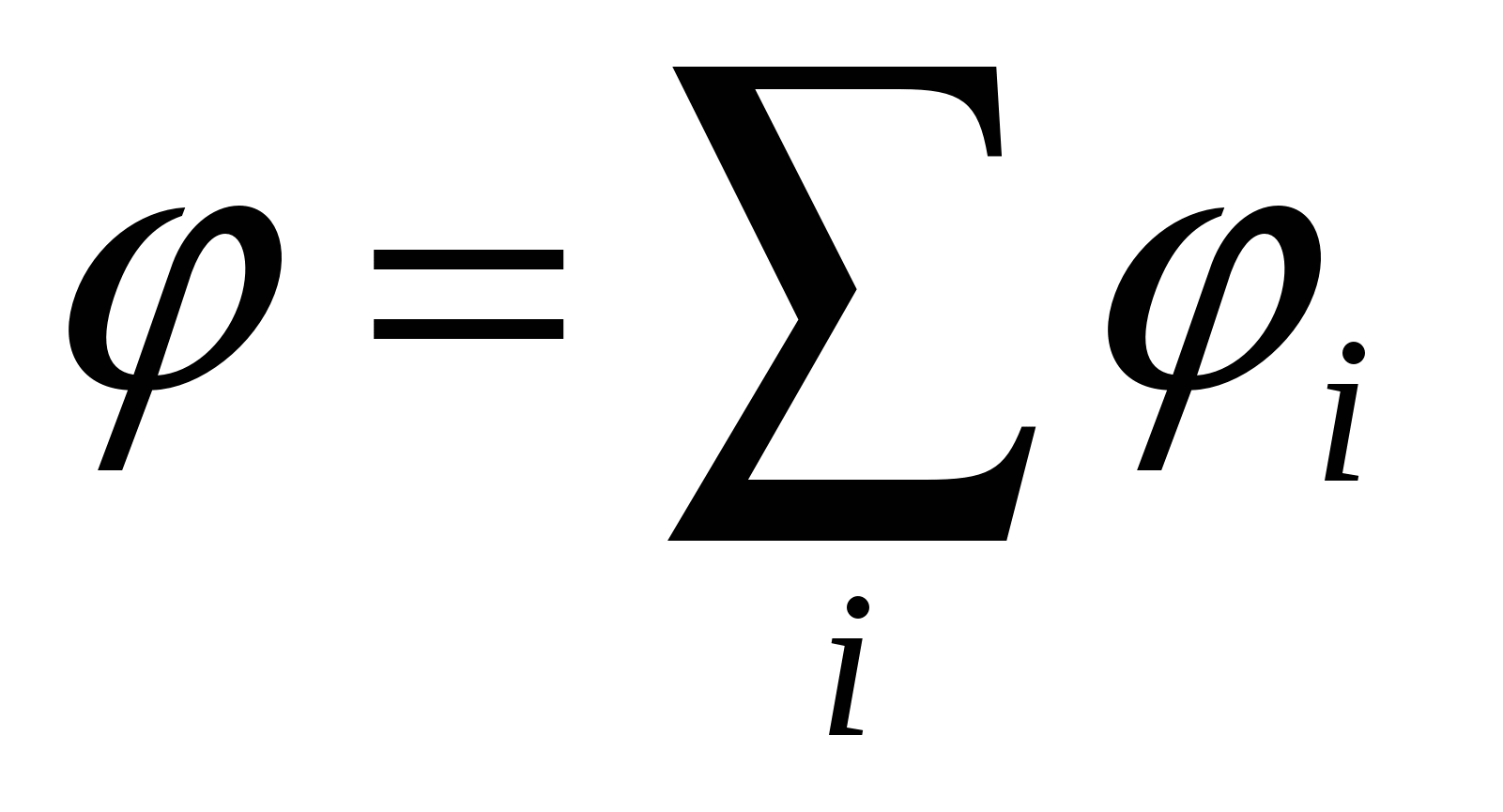 , , 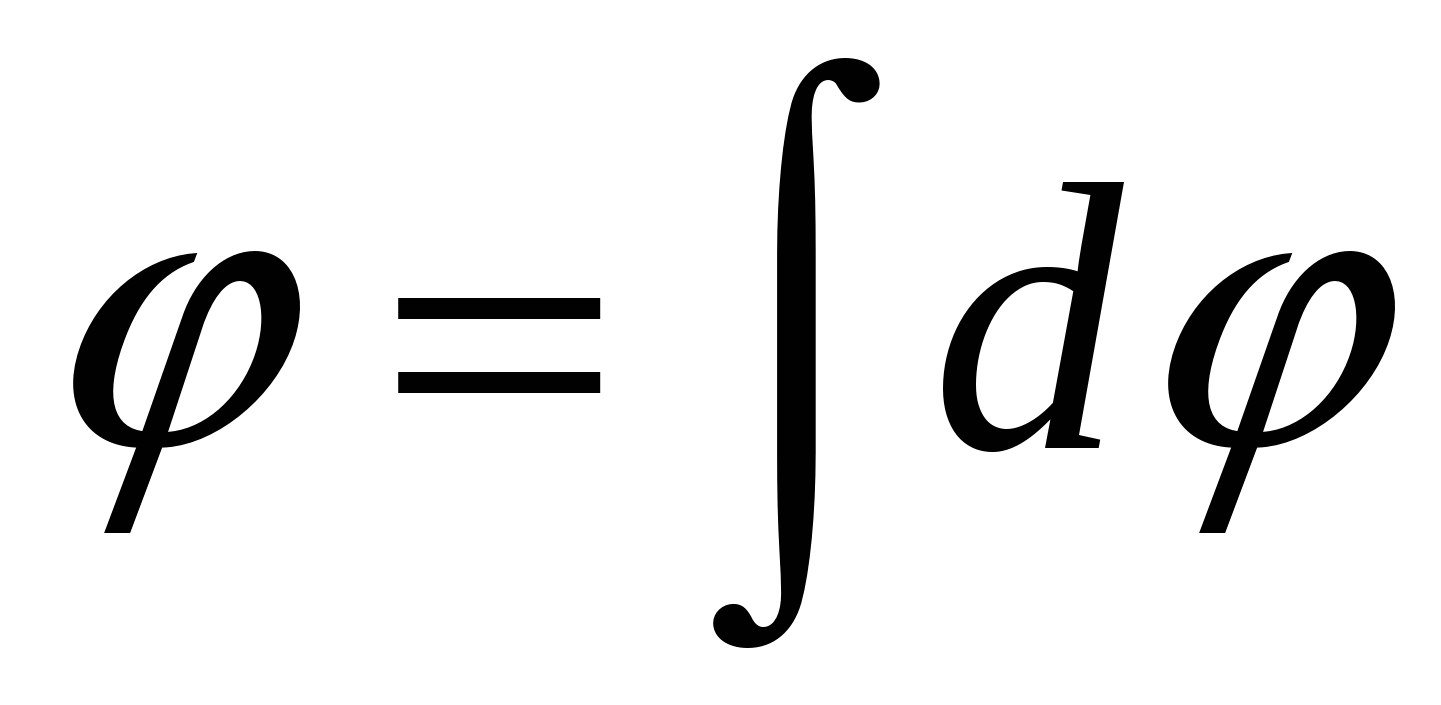 - принцип суперпозиции; - принцип суперпозиции;
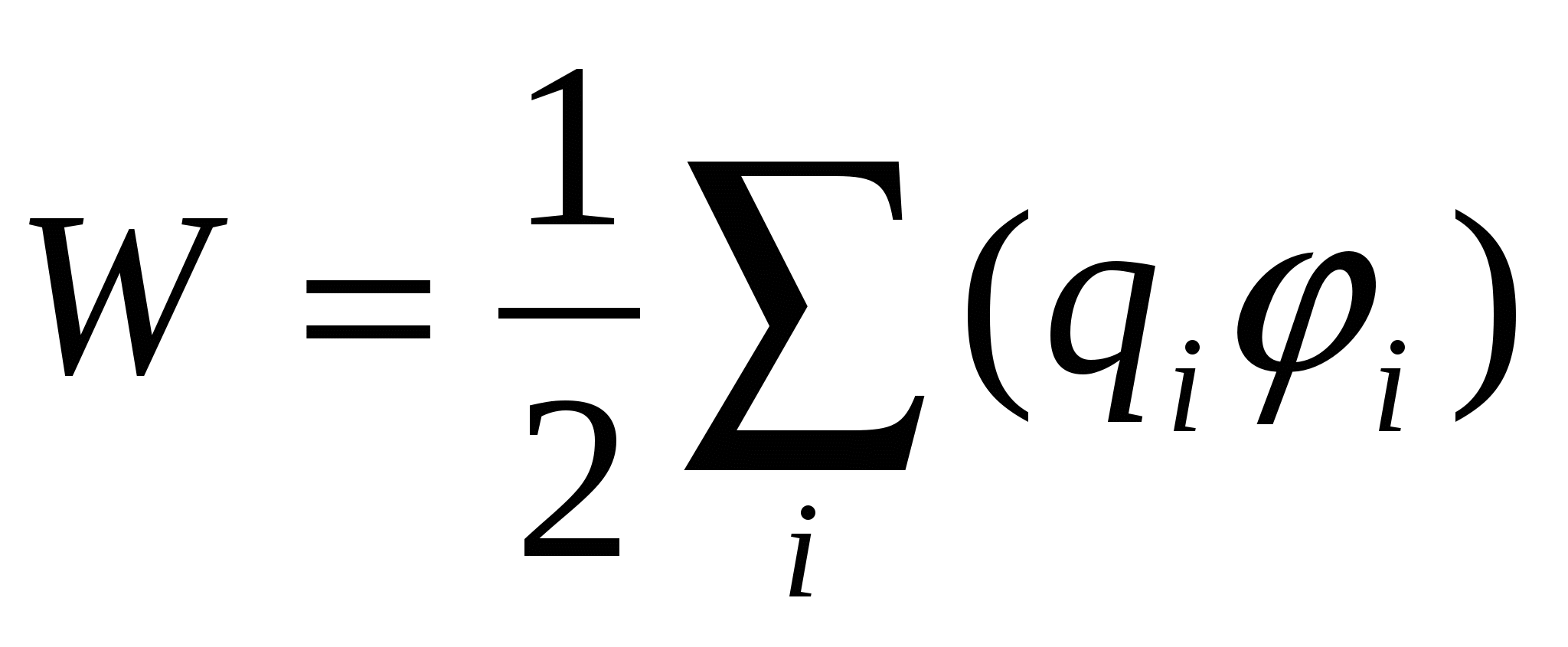 - потенциальная энергия системы точечных зарядов; - потенциальная энергия системы точечных зарядов;
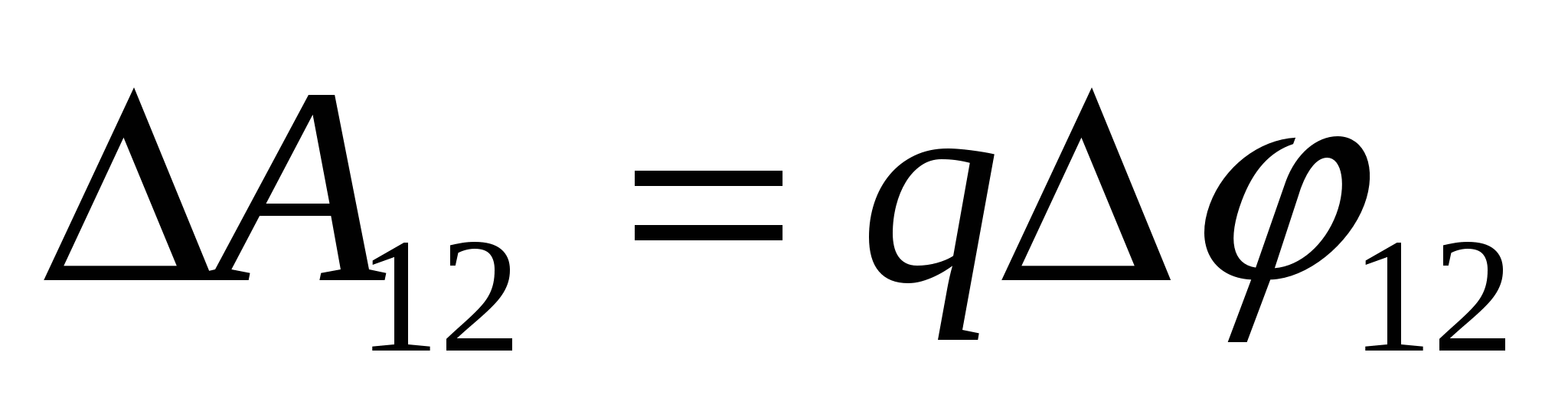 - работа поля по перемещению заряда; - работа поля по перемещению заряда;
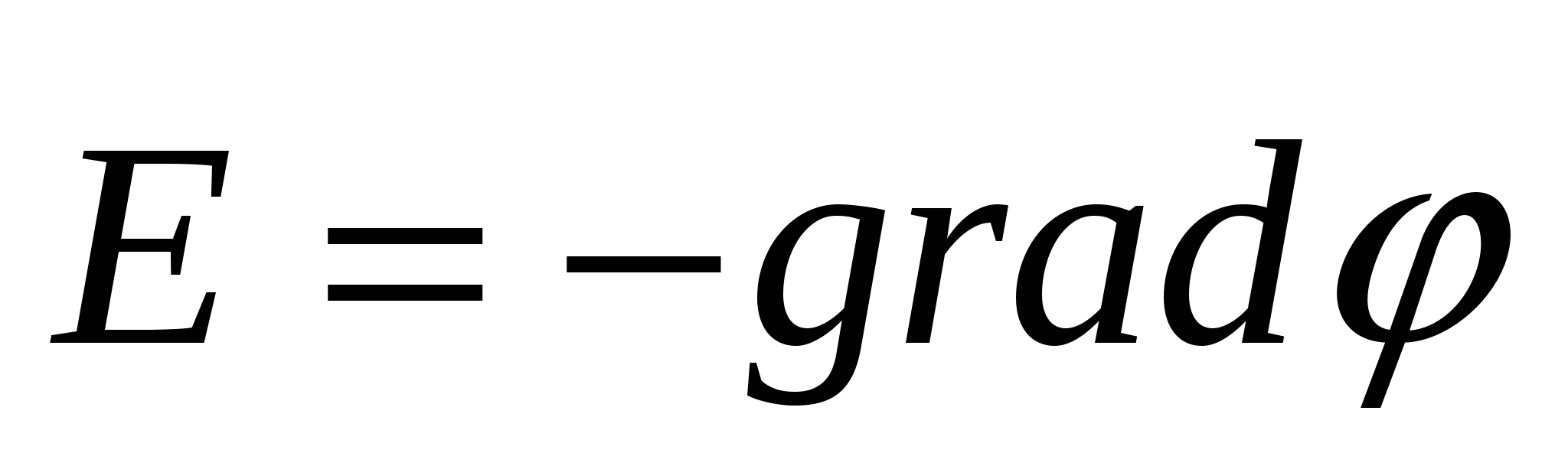 , ,  , , 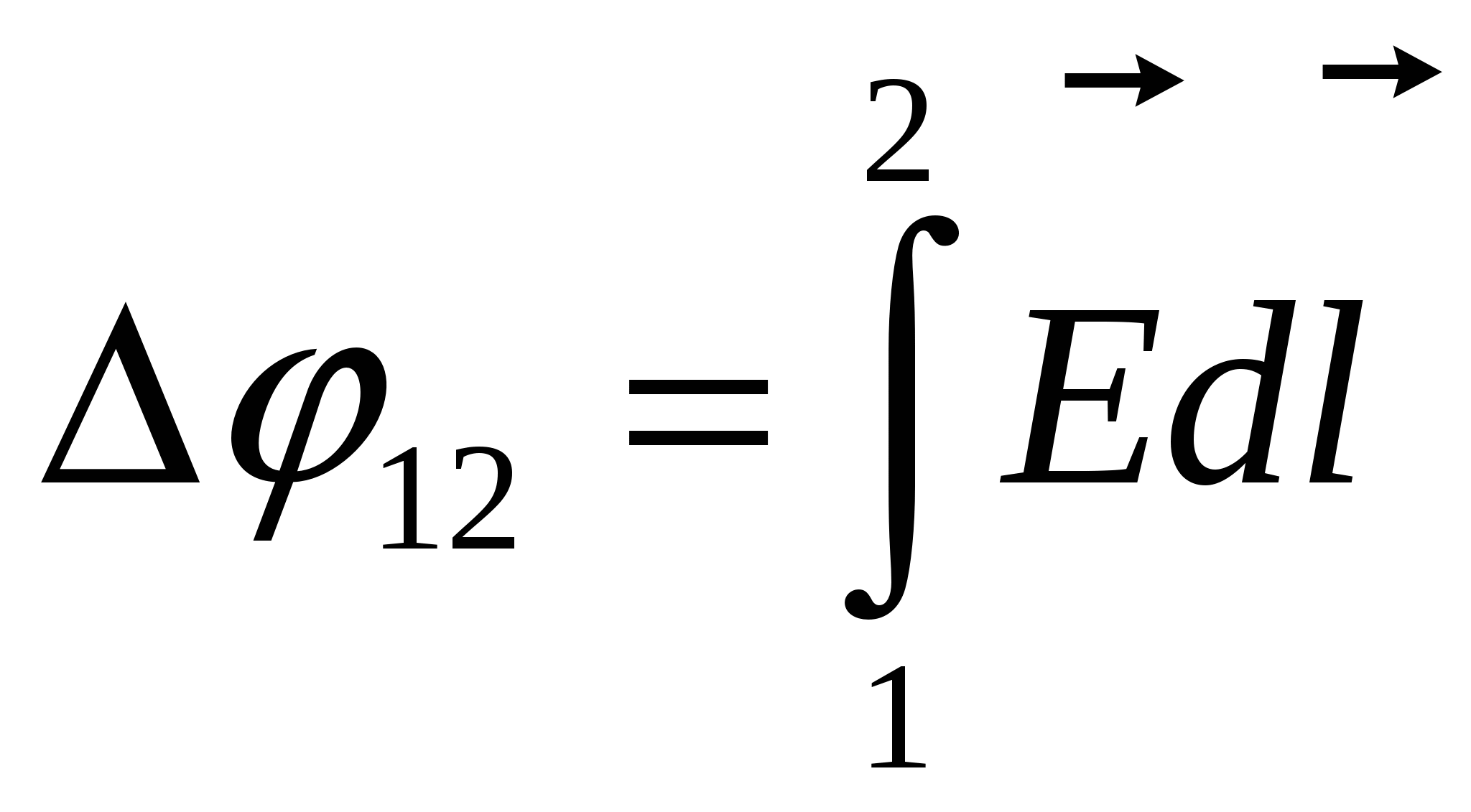 - связь напряженности и потенциала. - связь напряженности и потенциала.
4. Поляризация диэлектриков. Диполь
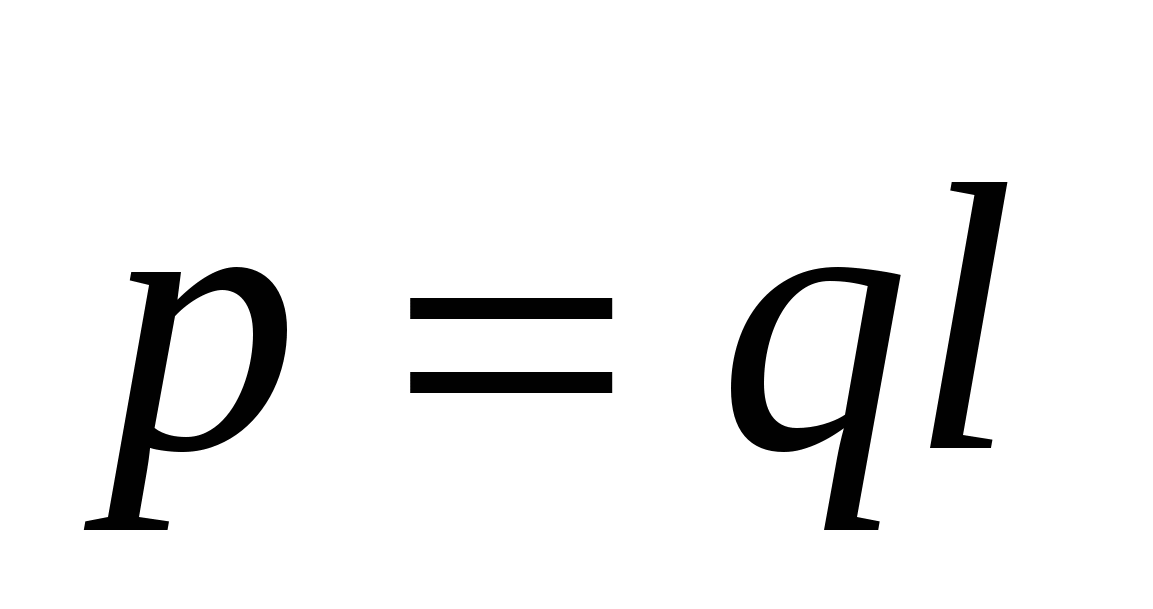 - электрический дипольный момент; - электрический дипольный момент;
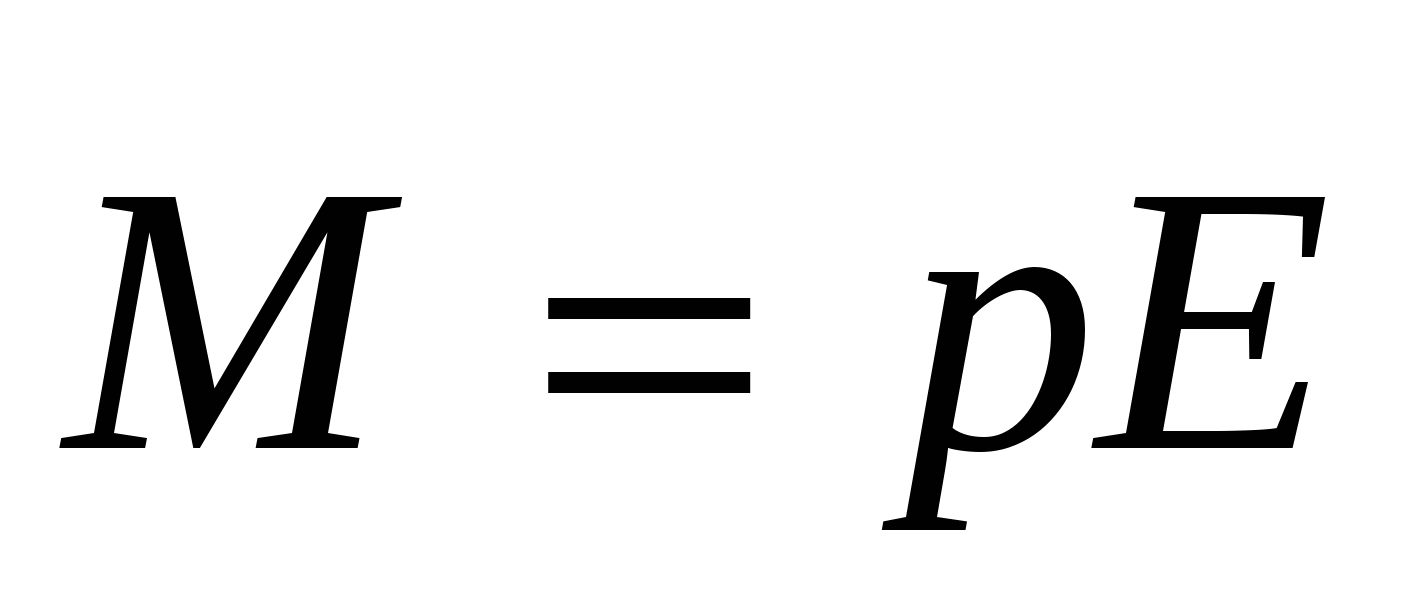 - момент силы, действующий на диполь в электрическом поле; - момент силы, действующий на диполь в электрическом поле;
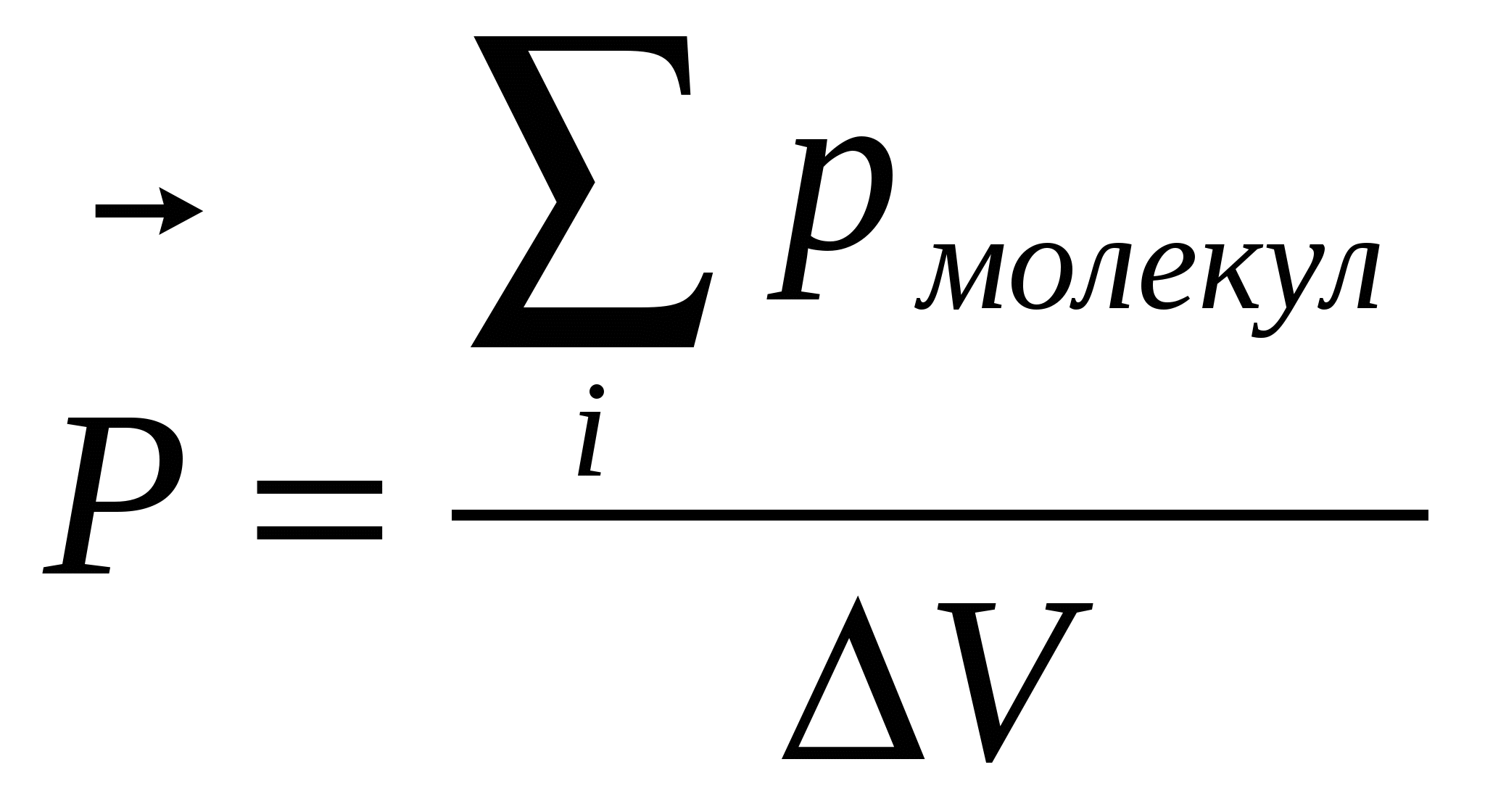 , , 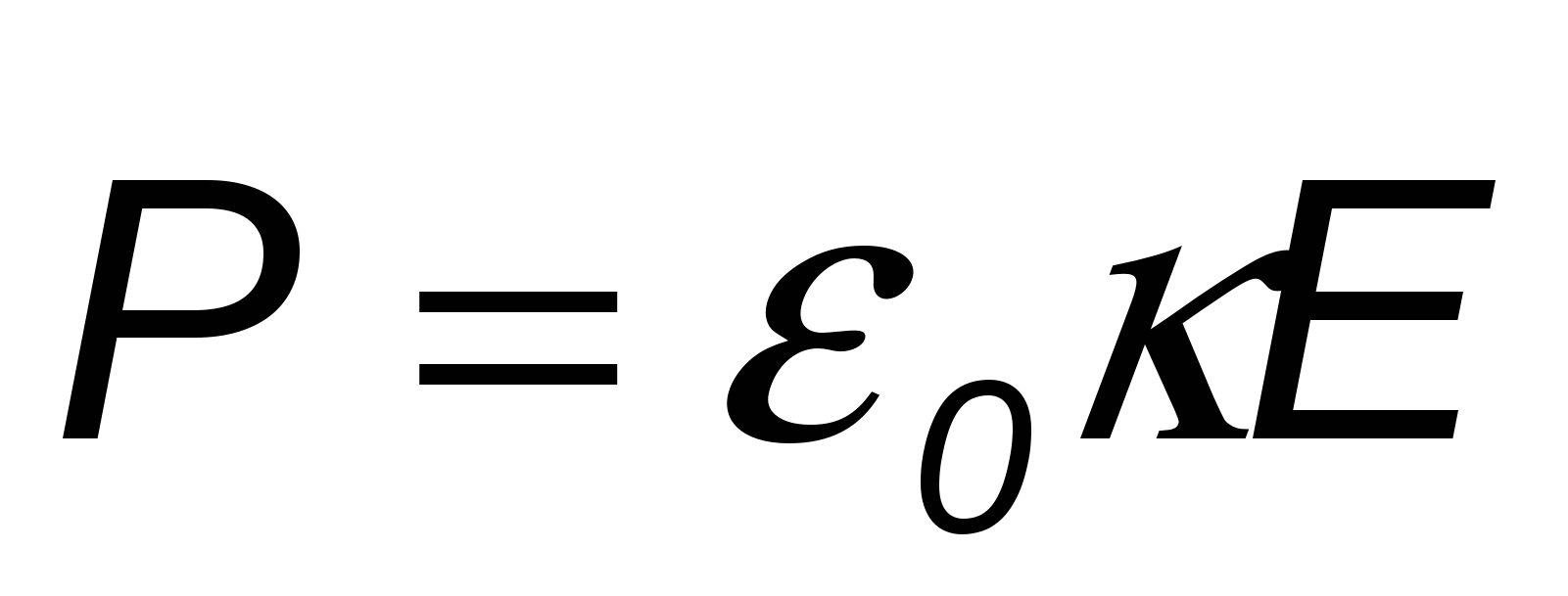 - поляризованность (вектор поляризации) диэлектрика; - поляризованность (вектор поляризации) диэлектрика;
 , где , где 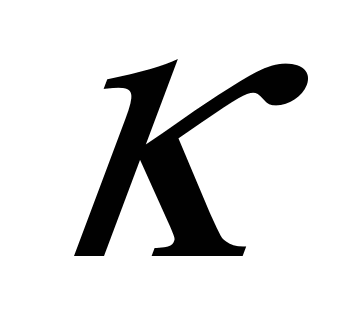 - диэлектрическая восприимчивость диэлектрика; - диэлектрическая восприимчивость диэлектрика;
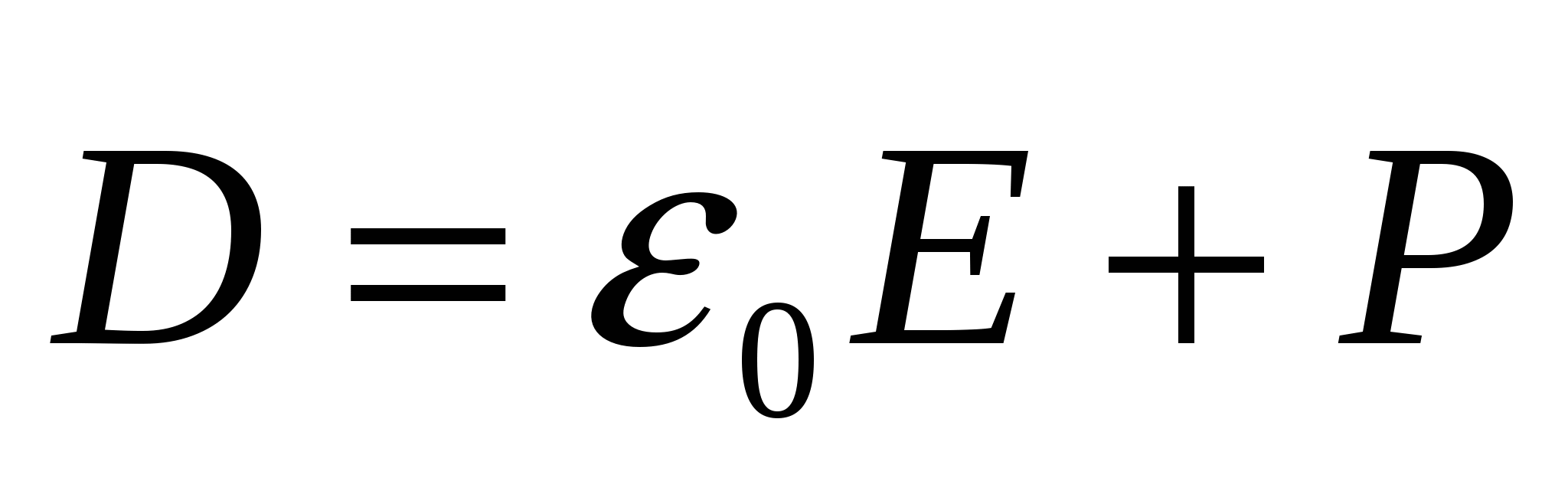 -вектор электрического смещения. -вектор электрического смещения.
5.Проводники. Емкость
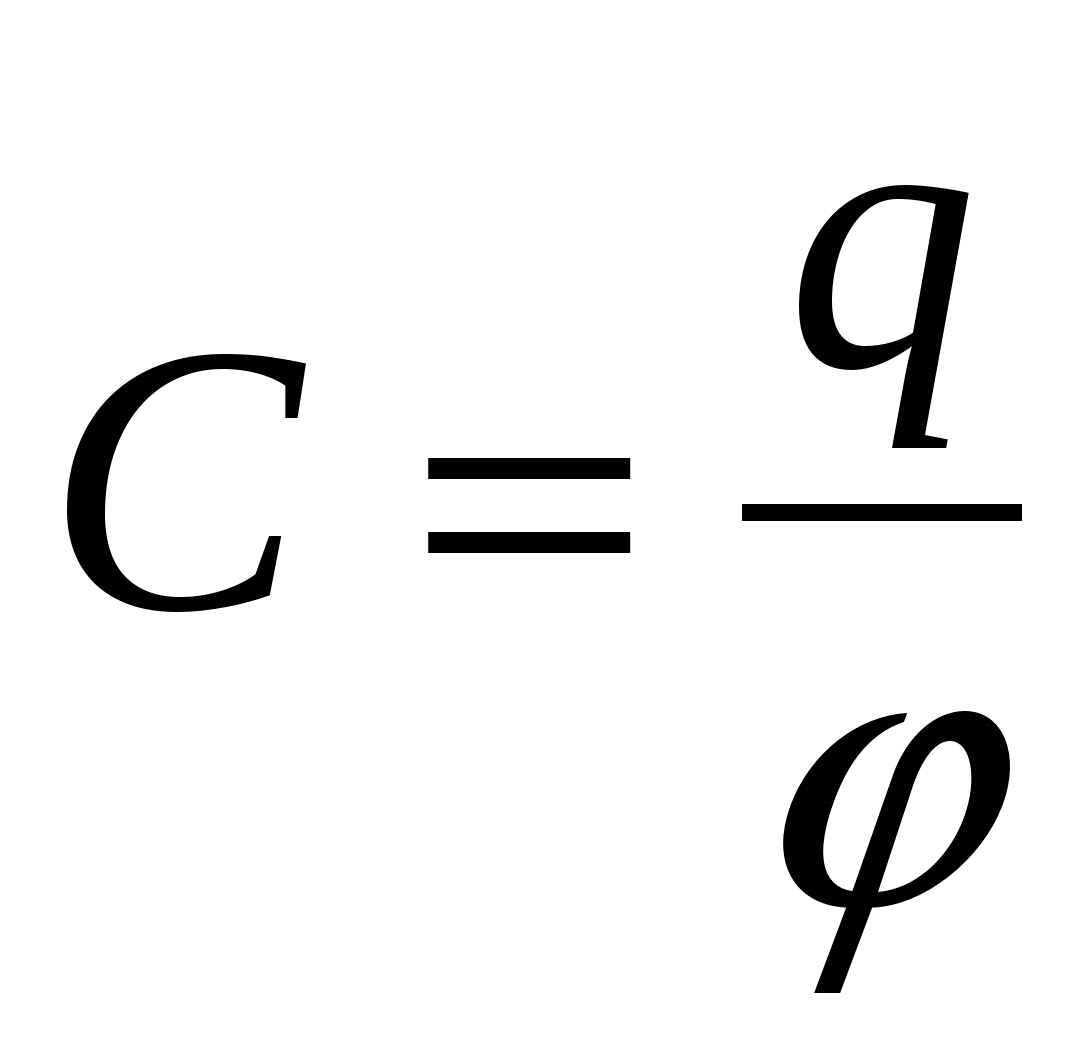 , , 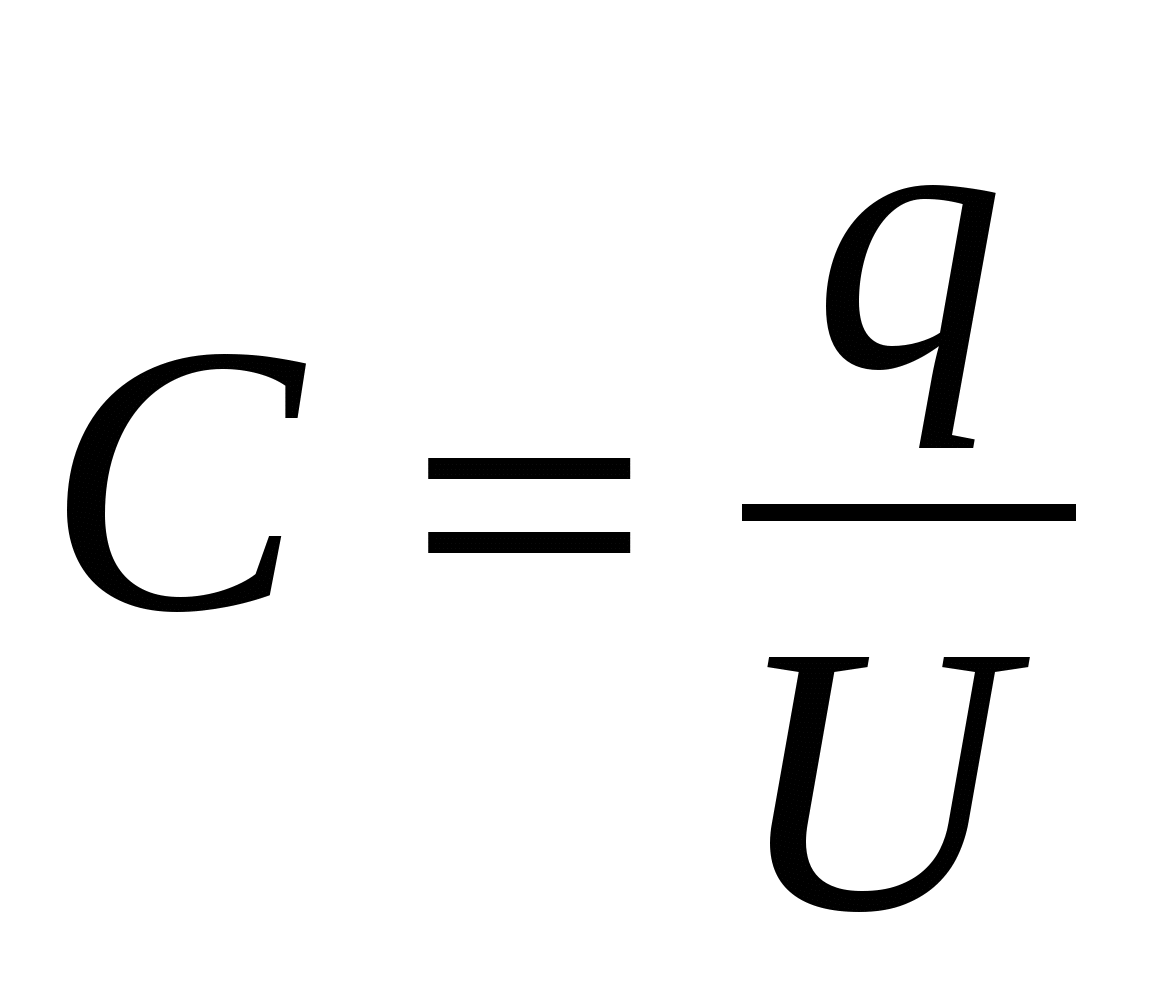 - определение емкости проводника, конденсатора; - определение емкости проводника, конденсатора;
 - емкость шара. - емкость шара.
6. Заряженная частица в электрическом поле
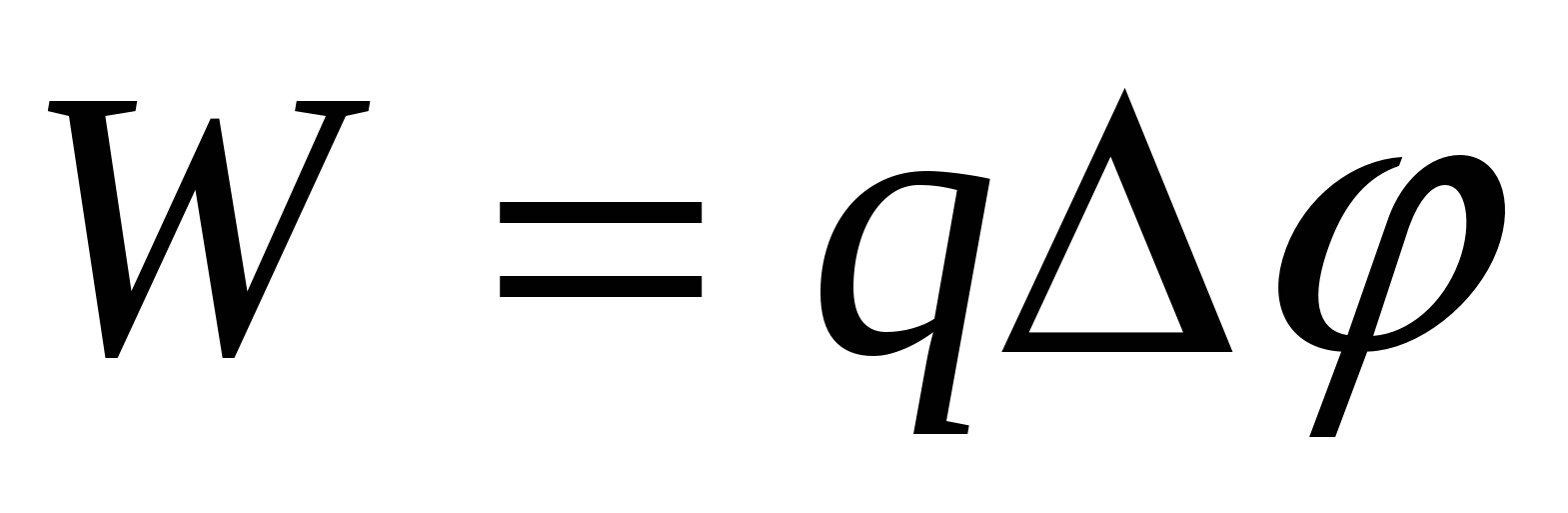 - энергия, приобретенная заряженной частицей в электрическом поле; - энергия, приобретенная заряженной частицей в электрическом поле;
 - связь между напряженностью поля и напряжением на конденсаторе. - связь между напряженностью поля и напряжением на конденсаторе.
7. Конденсаторы. Емкость
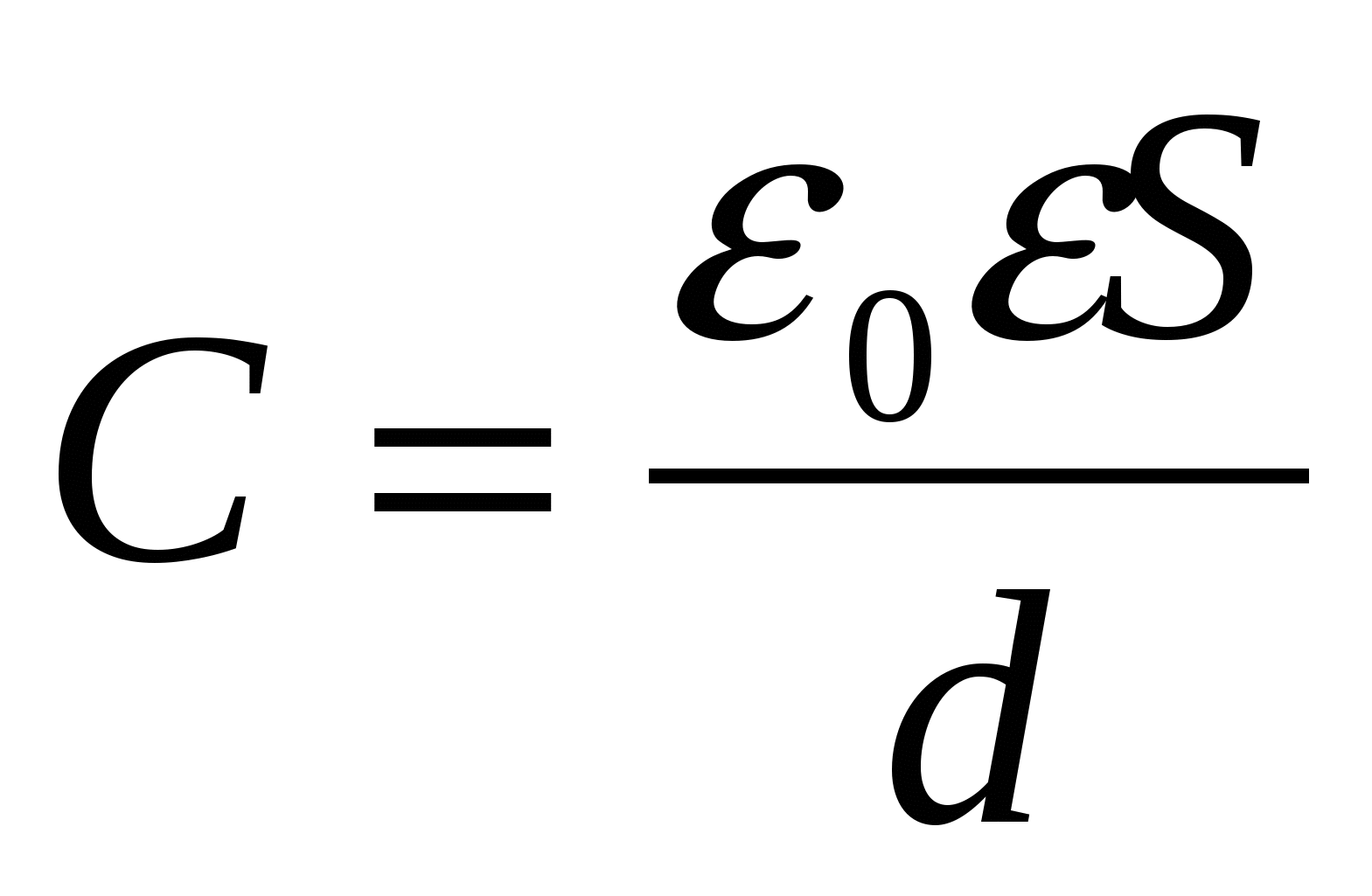 - емкость плоского конденсатора; - емкость плоского конденсатора;
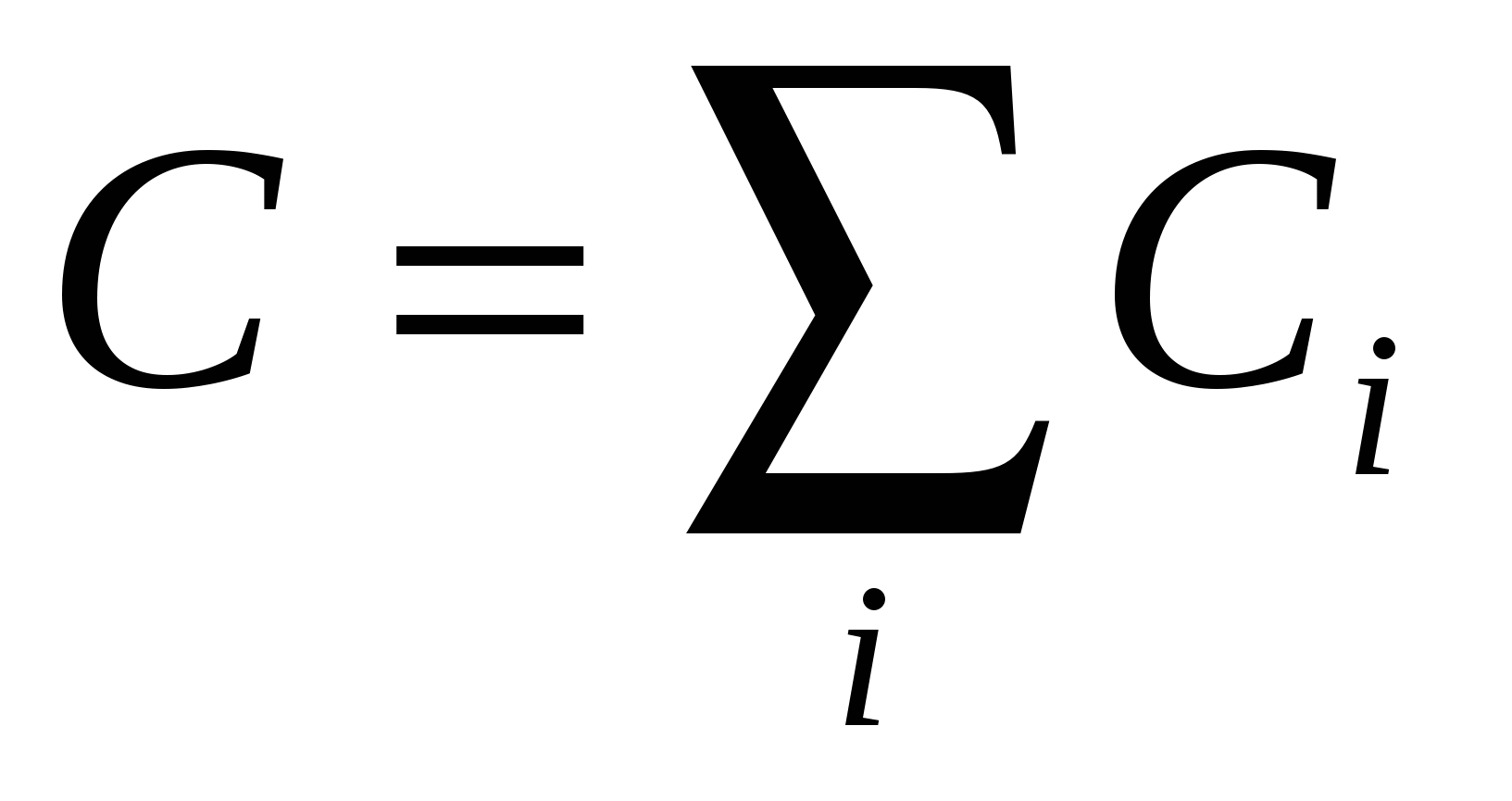 - общая емкость при параллельном соединении конденсаторов; - общая емкость при параллельном соединении конденсаторов;
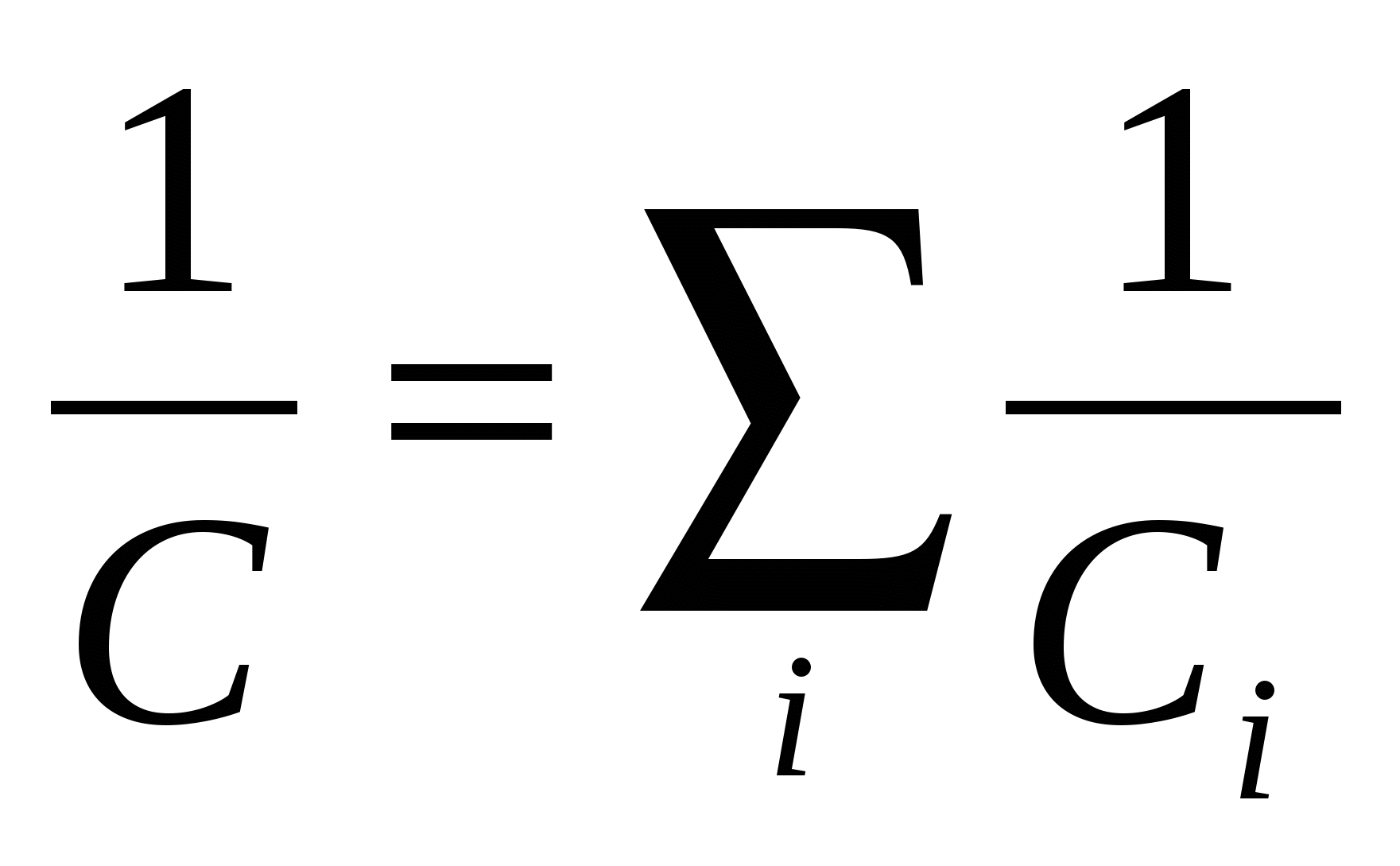 - общая емкость при последовательном соединении конденсаторов. - общая емкость при последовательном соединении конденсаторов.
8. Энергия электростатического поля. Плотность энергии поля
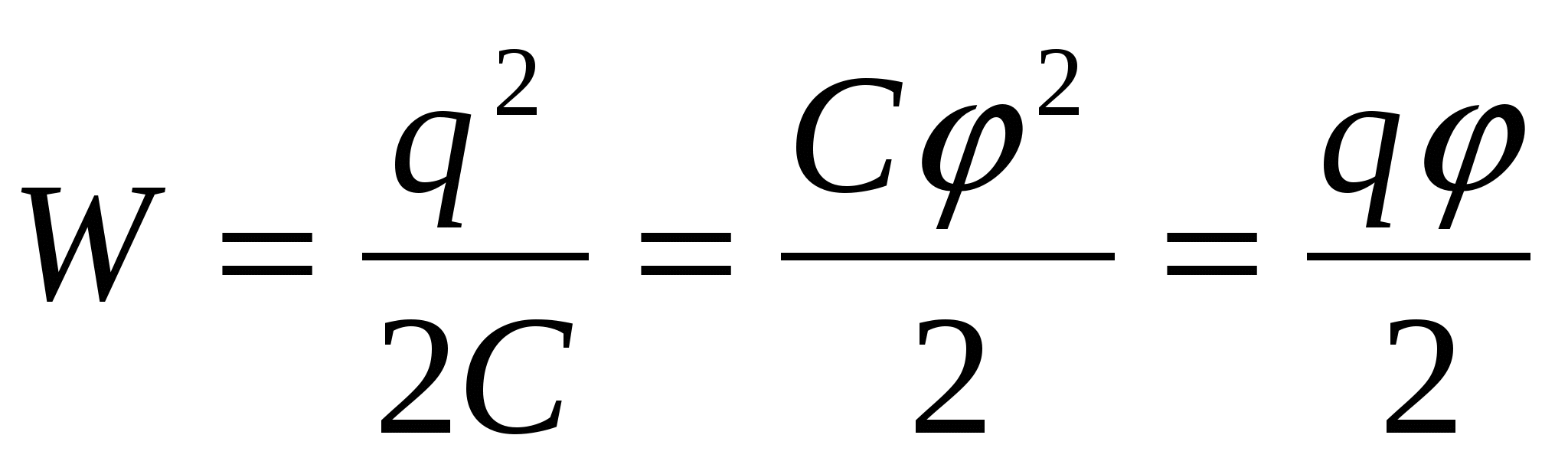 - энергия заряженного проводника; - энергия заряженного проводника;
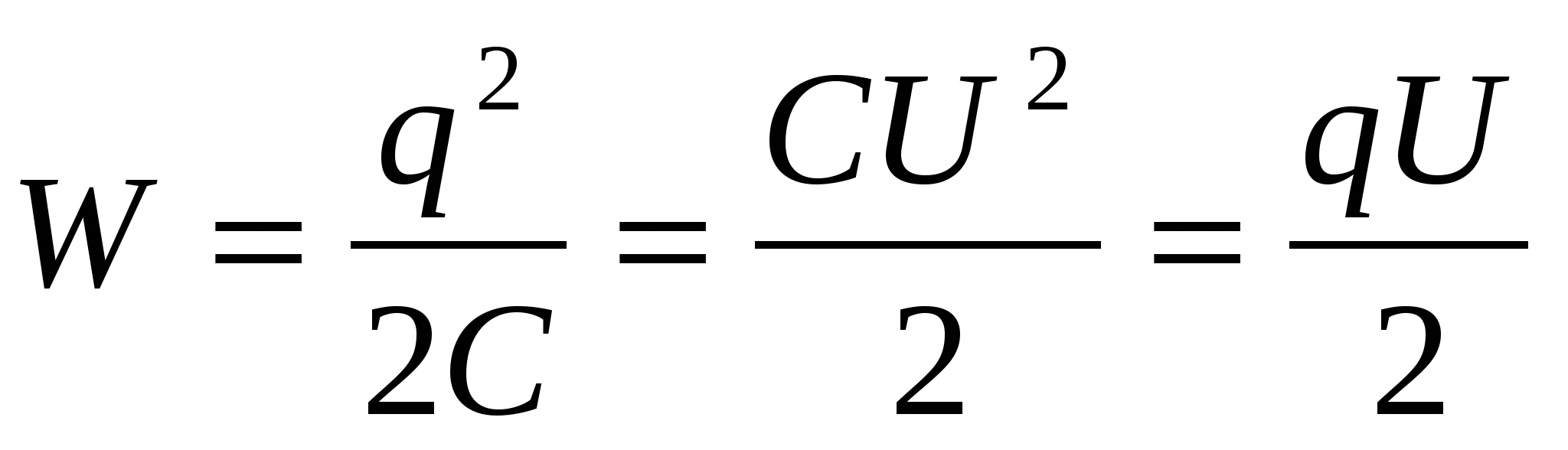 - энергия заряженного конденсатора; - энергия заряженного конденсатора;
 - связь между консервативной силой и потенциальной энергией; - связь между консервативной силой и потенциальной энергией;
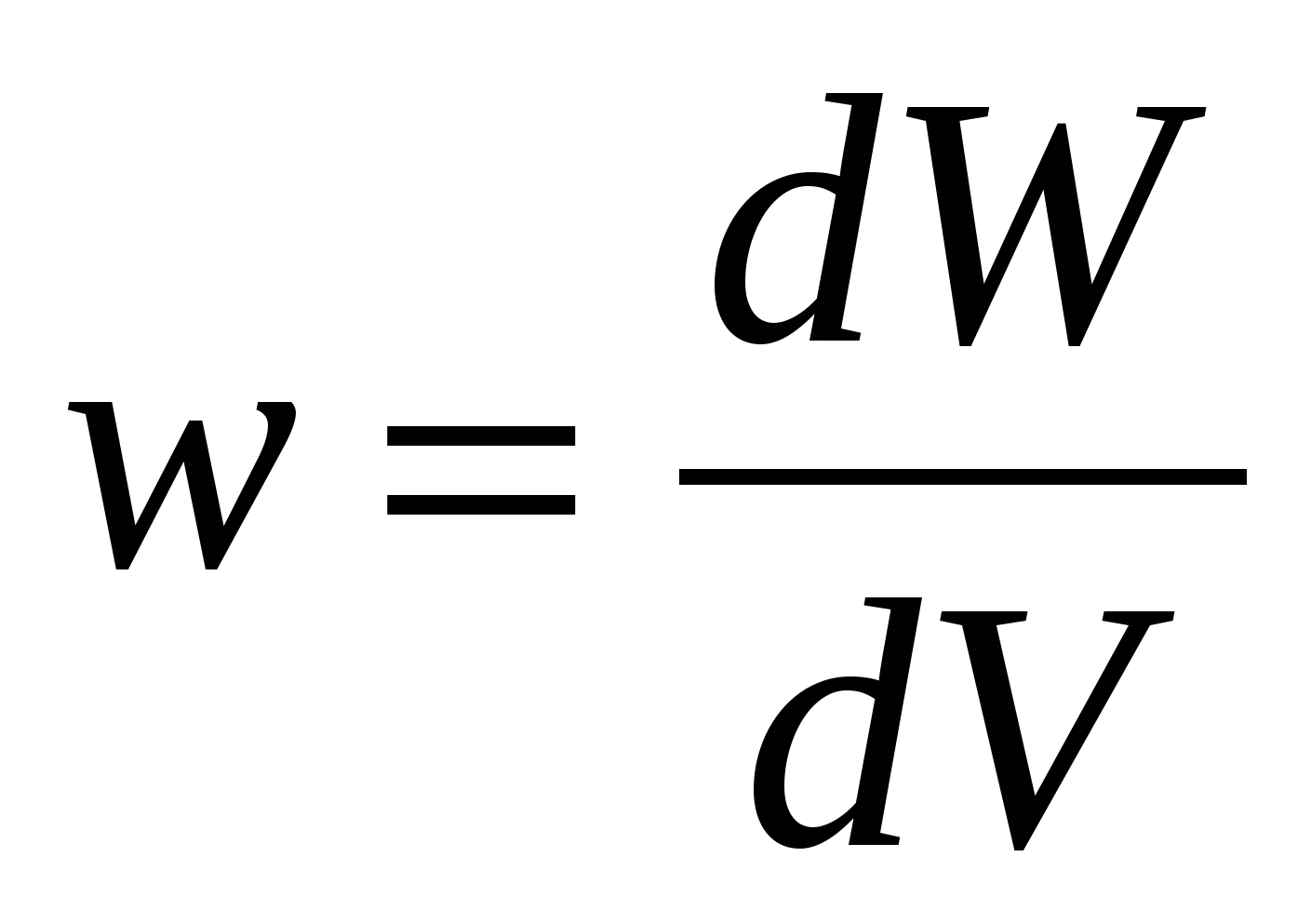 - определение объемной плотности энергии поля; - определение объемной плотности энергии поля;
 - объемная плотность энергии электростатического поля. - объемная плотность энергии электростатического поля.
9. Электрический ток. Законы Ома и Кирхгофа
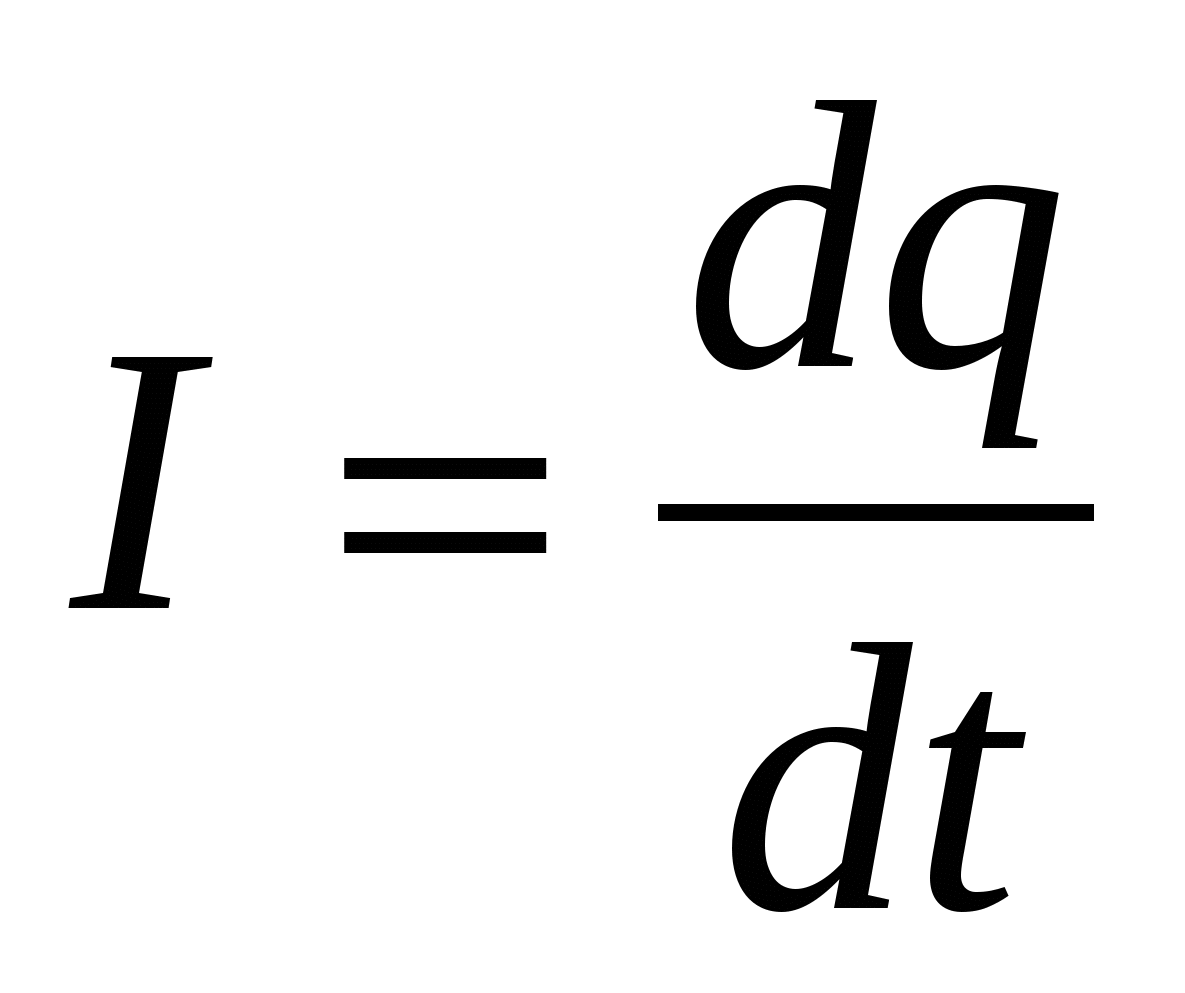 - определение силы тока; - определение силы тока;
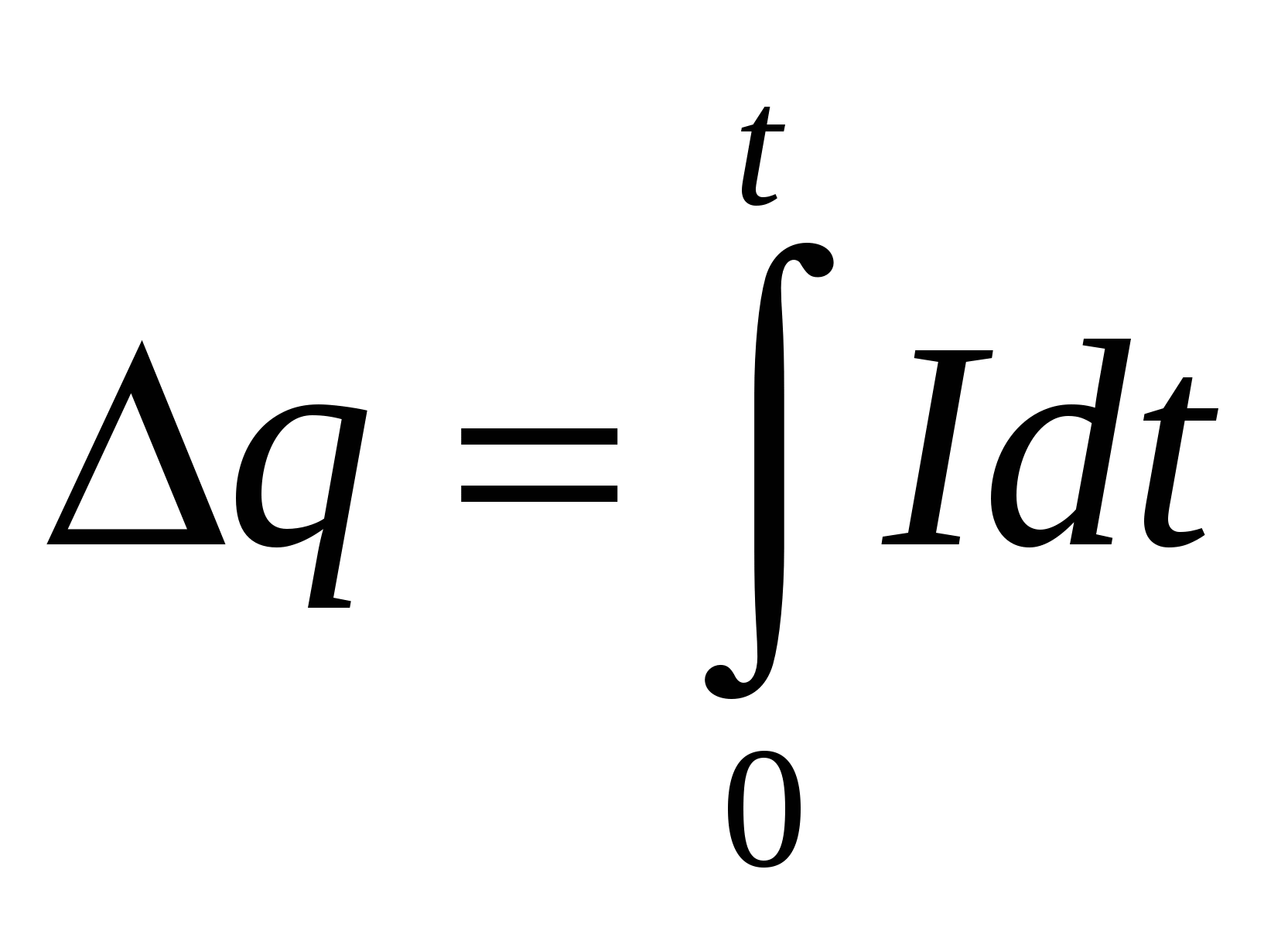 - заряд, прошедший через сечение проводника; - заряд, прошедший через сечение проводника;
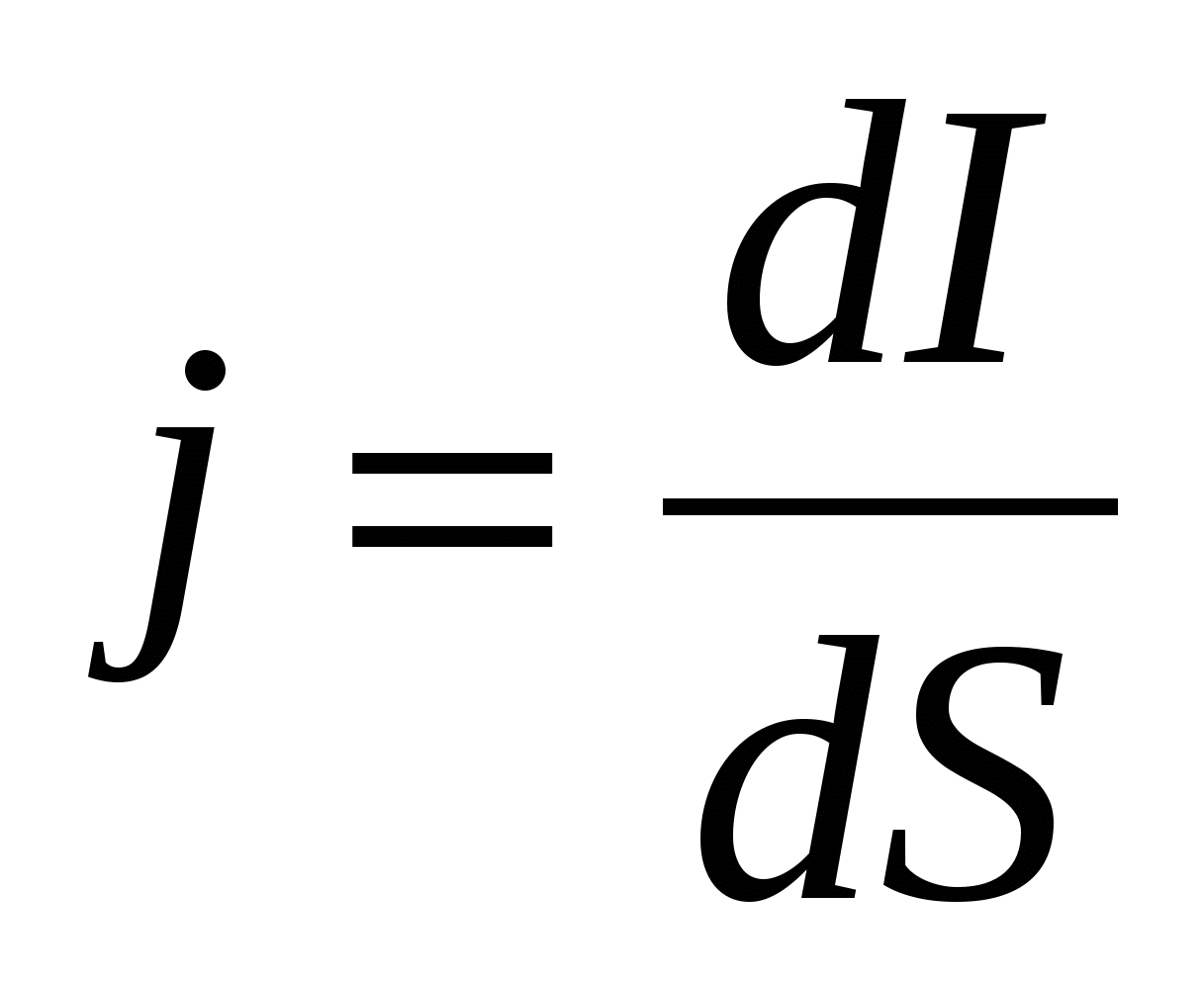 - определение плотности тока; - определение плотности тока;
 - плотность тока при направленном движении заряженных частиц; - плотность тока при направленном движении заряженных частиц;
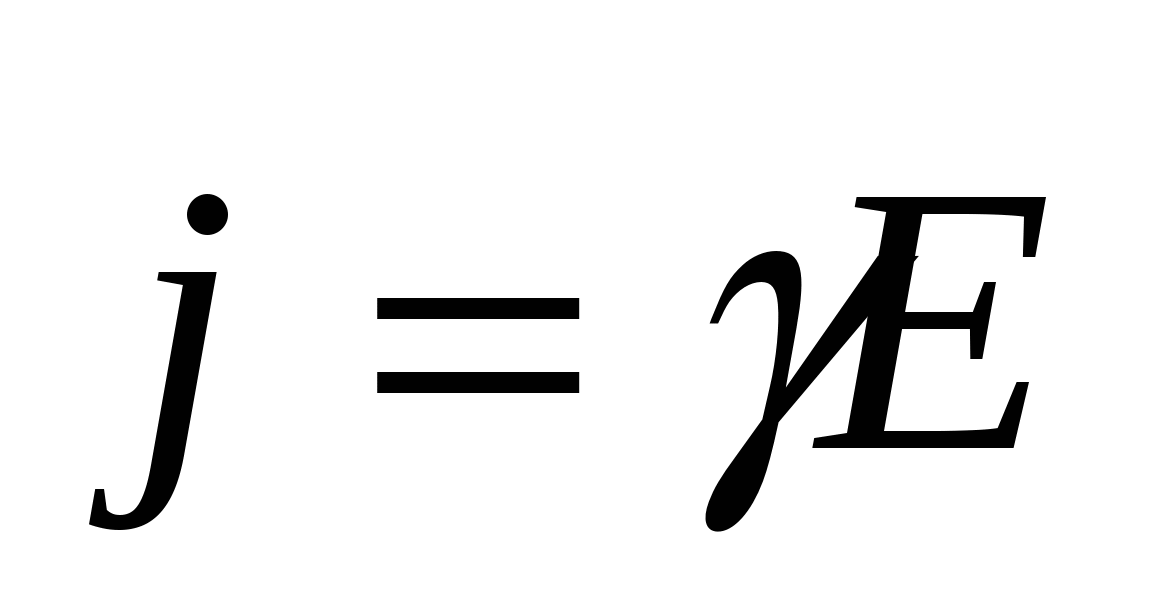 - закон Ома в локальной форме; - закон Ома в локальной форме;
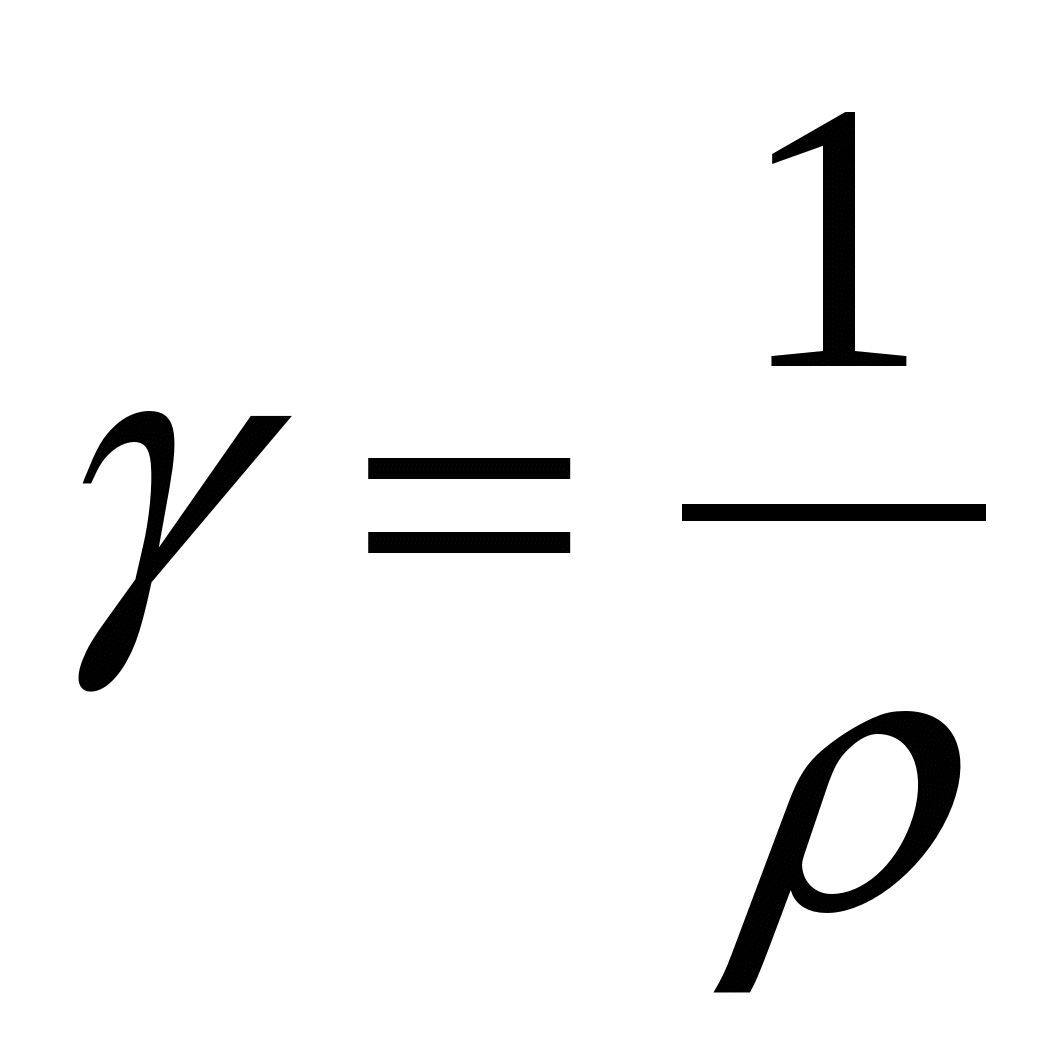 - связь удельной электропроводимости и удельного сопротивления; - связь удельной электропроводимости и удельного сопротивления;
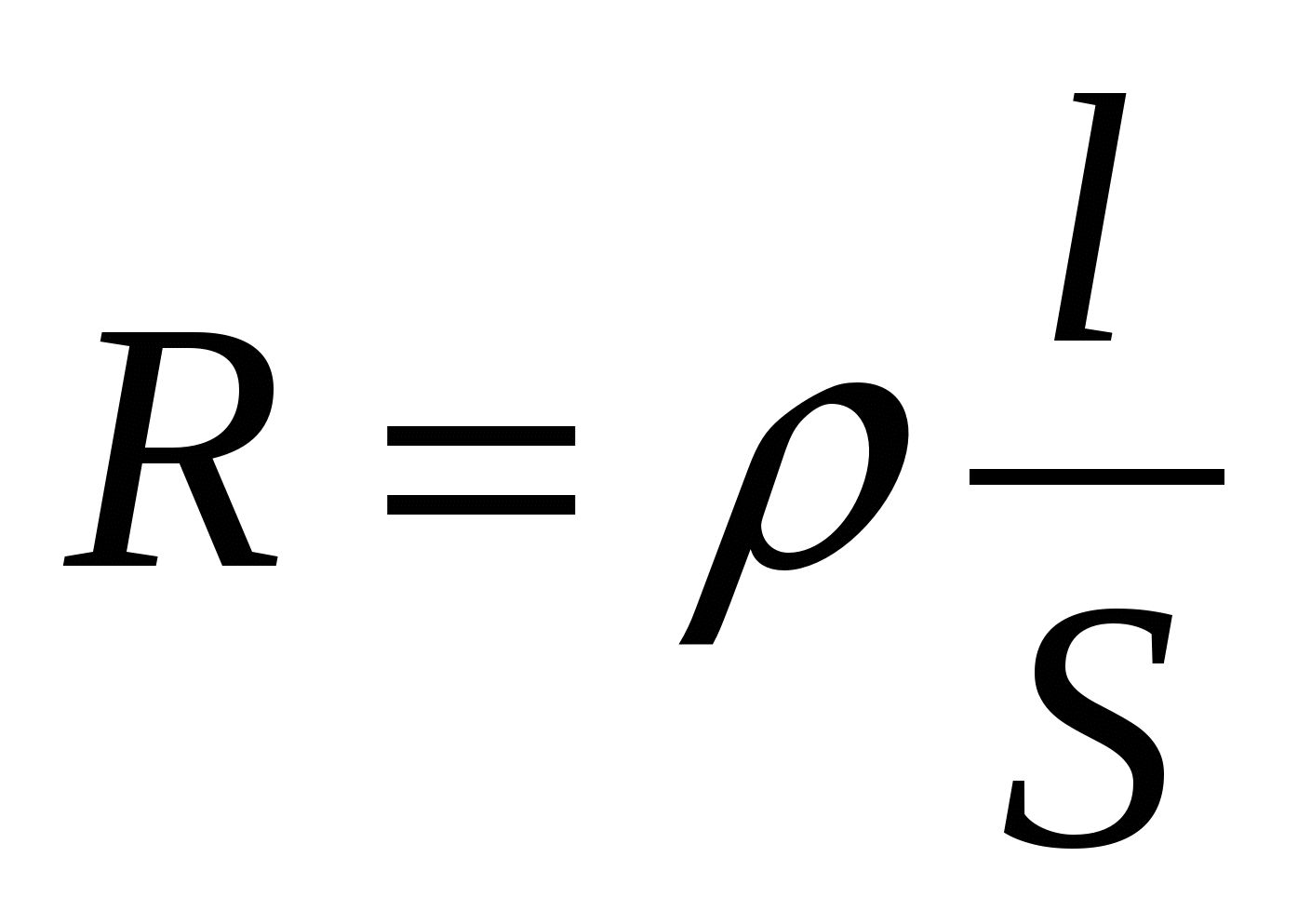 - сопротивление проводника; - сопротивление проводника;
 - общее сопротивление при последовательном соединении; - общее сопротивление при последовательном соединении;
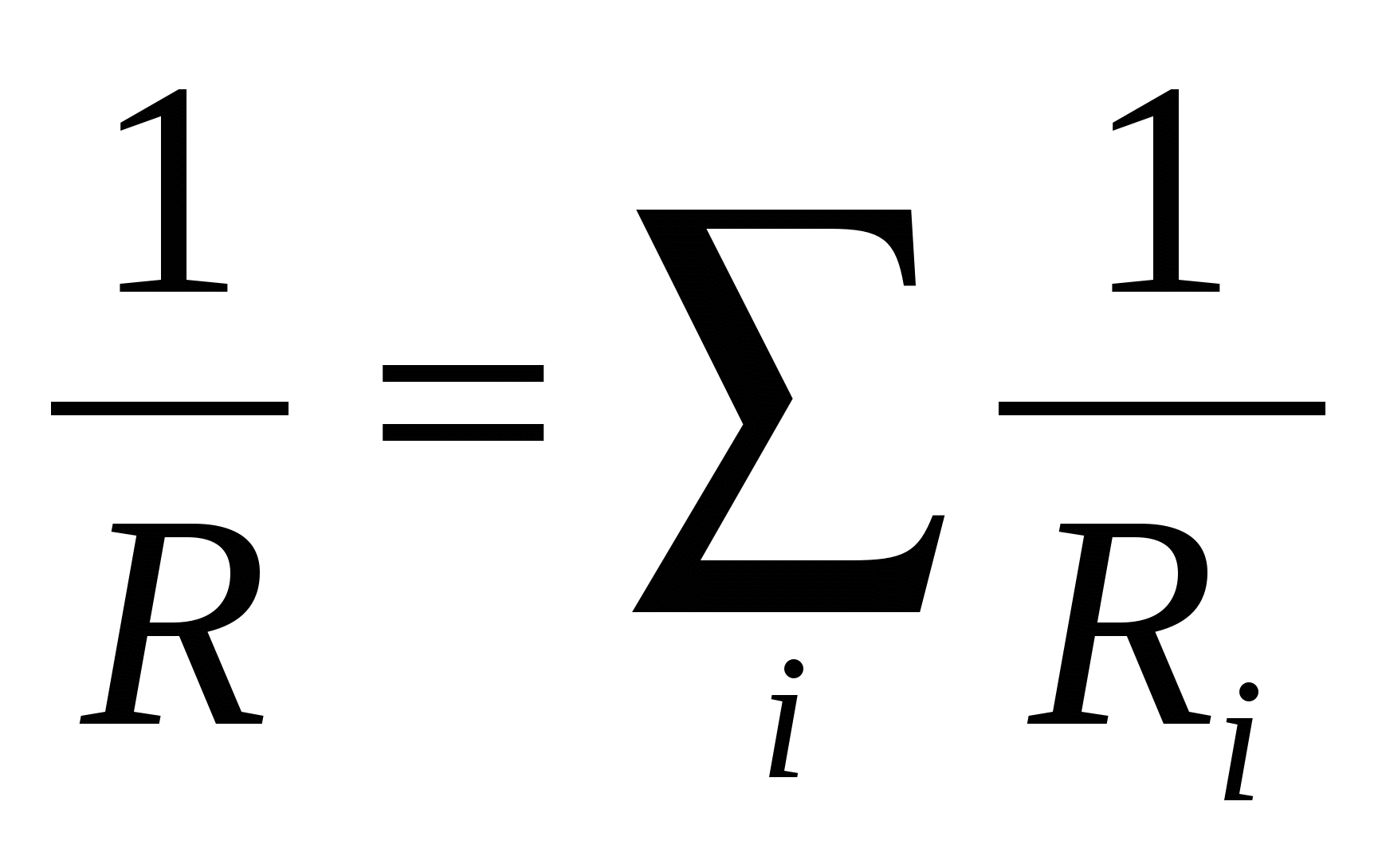 - общее сопротивление при параллельном соединении; - общее сопротивление при параллельном соединении;
 - закон Ома для однородного участка цепи; - закон Ома для однородного участка цепи;
U=Δφ+E - напряжение на неоднородном участке цепи;
E=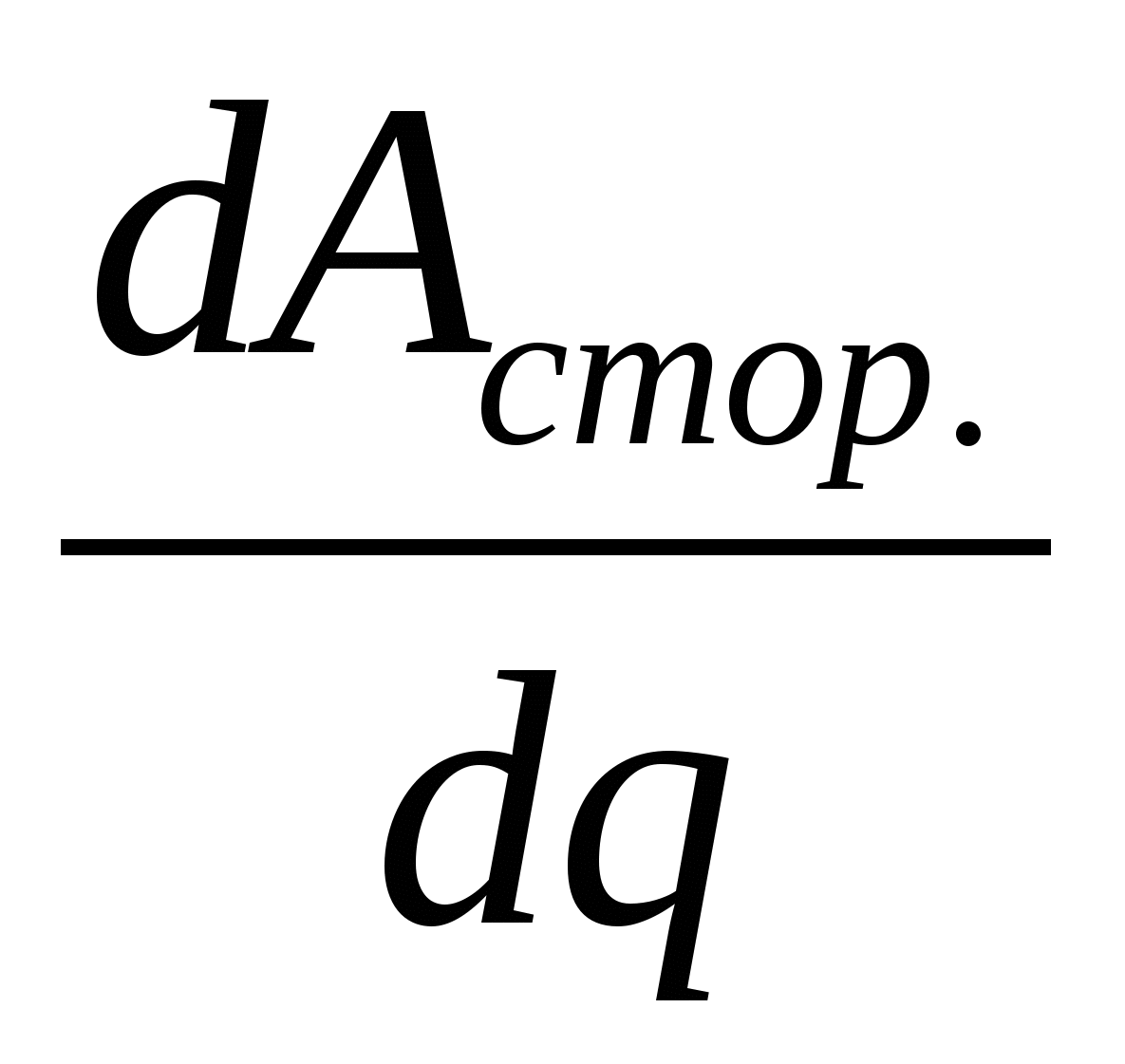 - определение электродвижущей силы; - определение электродвижущей силы;
E=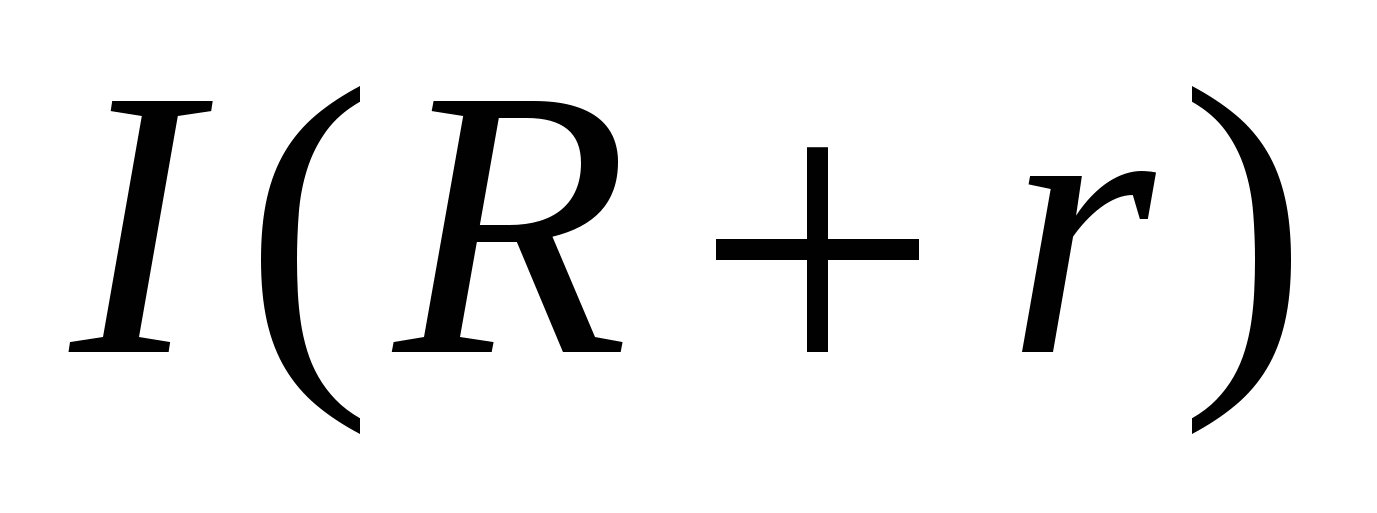 - закон Ома для замкнутой цепи; - закон Ома для замкнутой цепи;
 - первое правило Кирхгофа (для узла); - первое правило Кирхгофа (для узла);
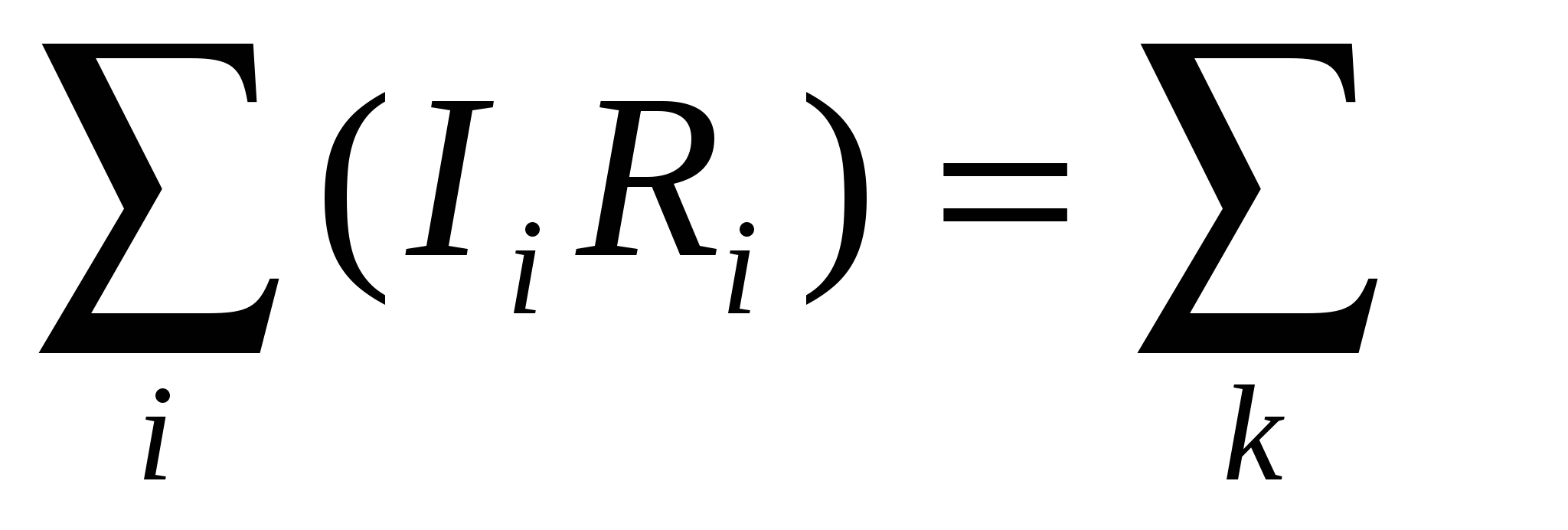 Ek - второе правило Кирхгофа (для замкнутого контура). Ek - второе правило Кирхгофа (для замкнутого контура).
10. Температурная зависимость сопротивления
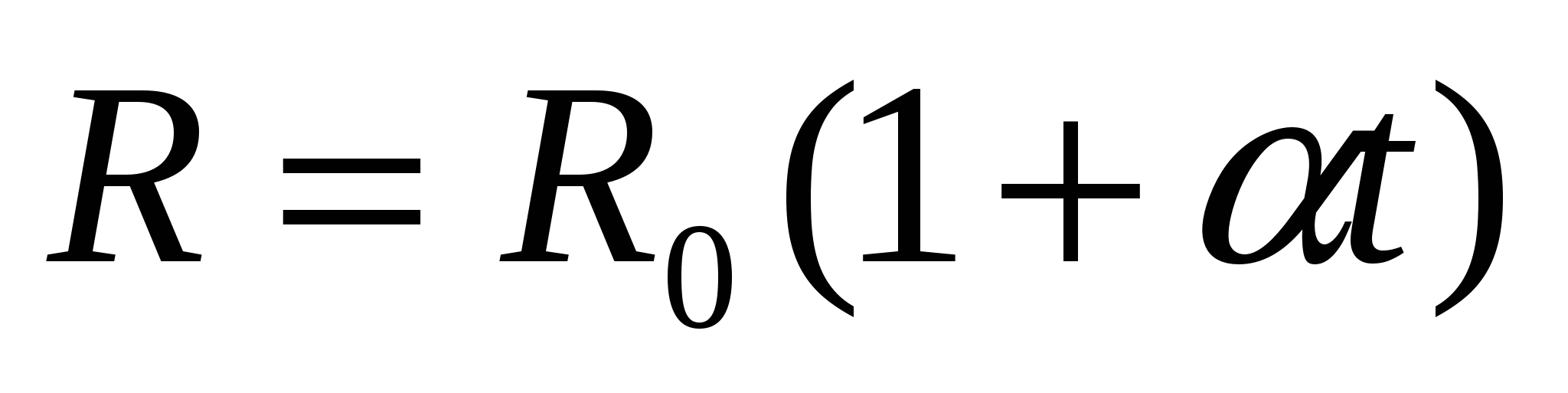 - зависимость сопротивления металла от температуры. - зависимость сопротивления металла от температуры.
11. Закон Джоуля-Ленца
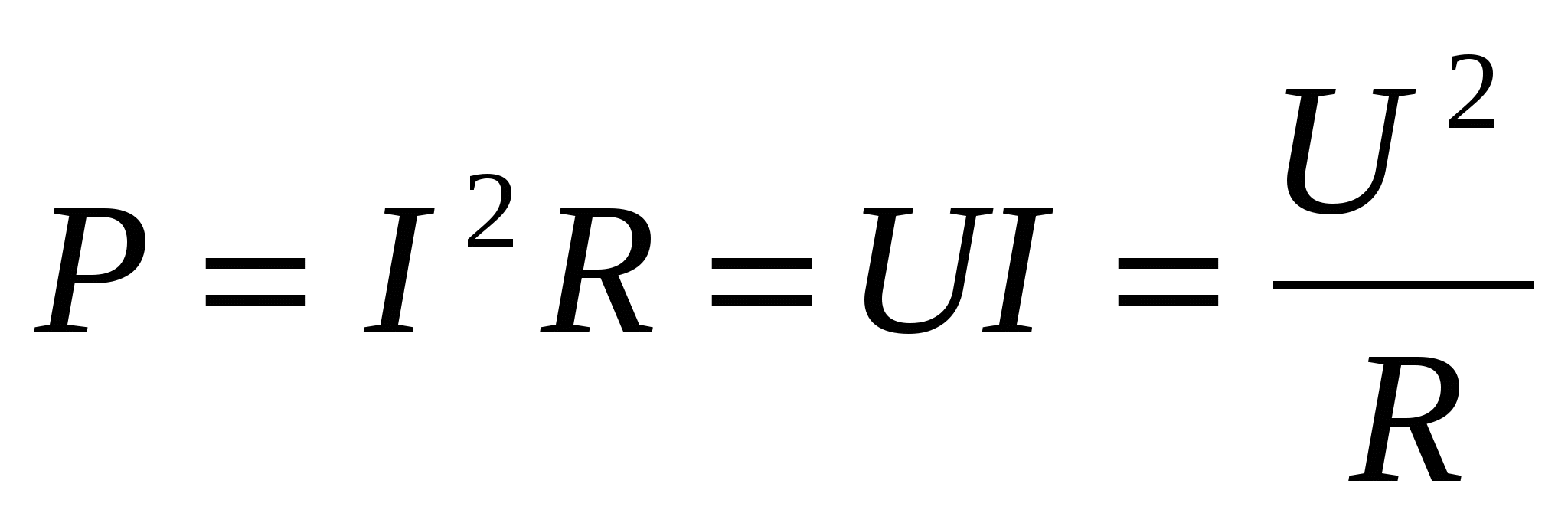 - полезная мощность тока; - полезная мощность тока;
 E - полная мощность источника; E - полная мощность источника;
 , , 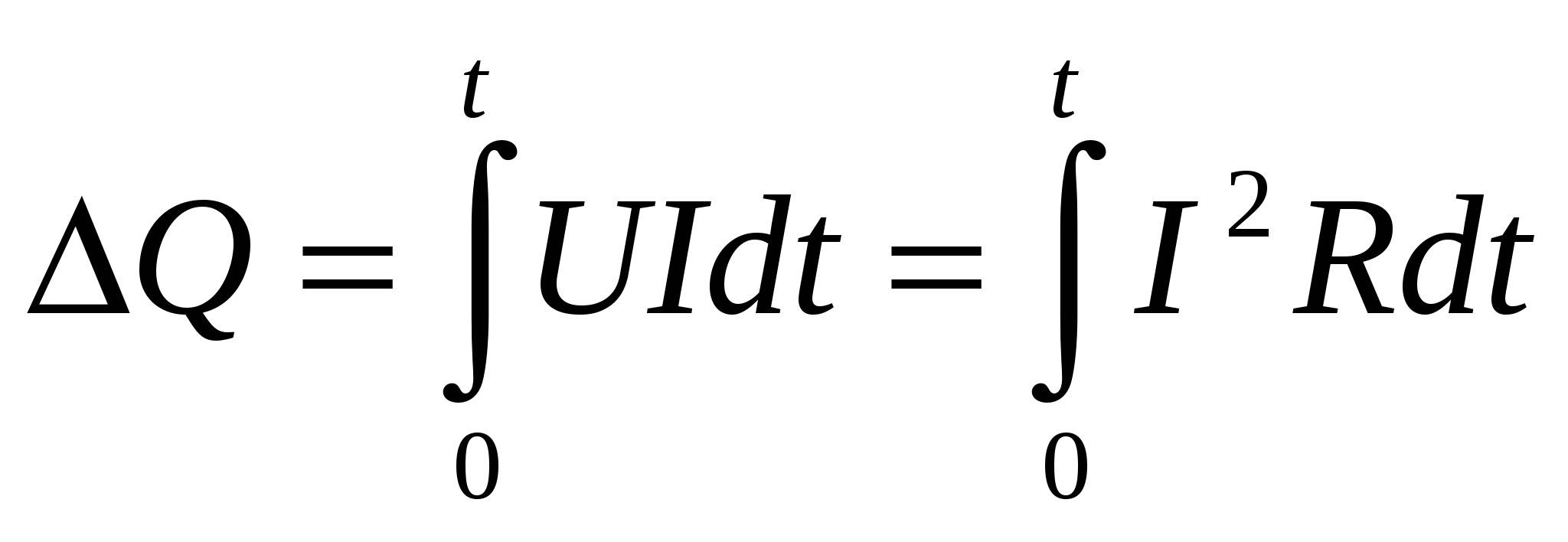 - закон Джоуля-Ленца; - закон Джоуля-Ленца;
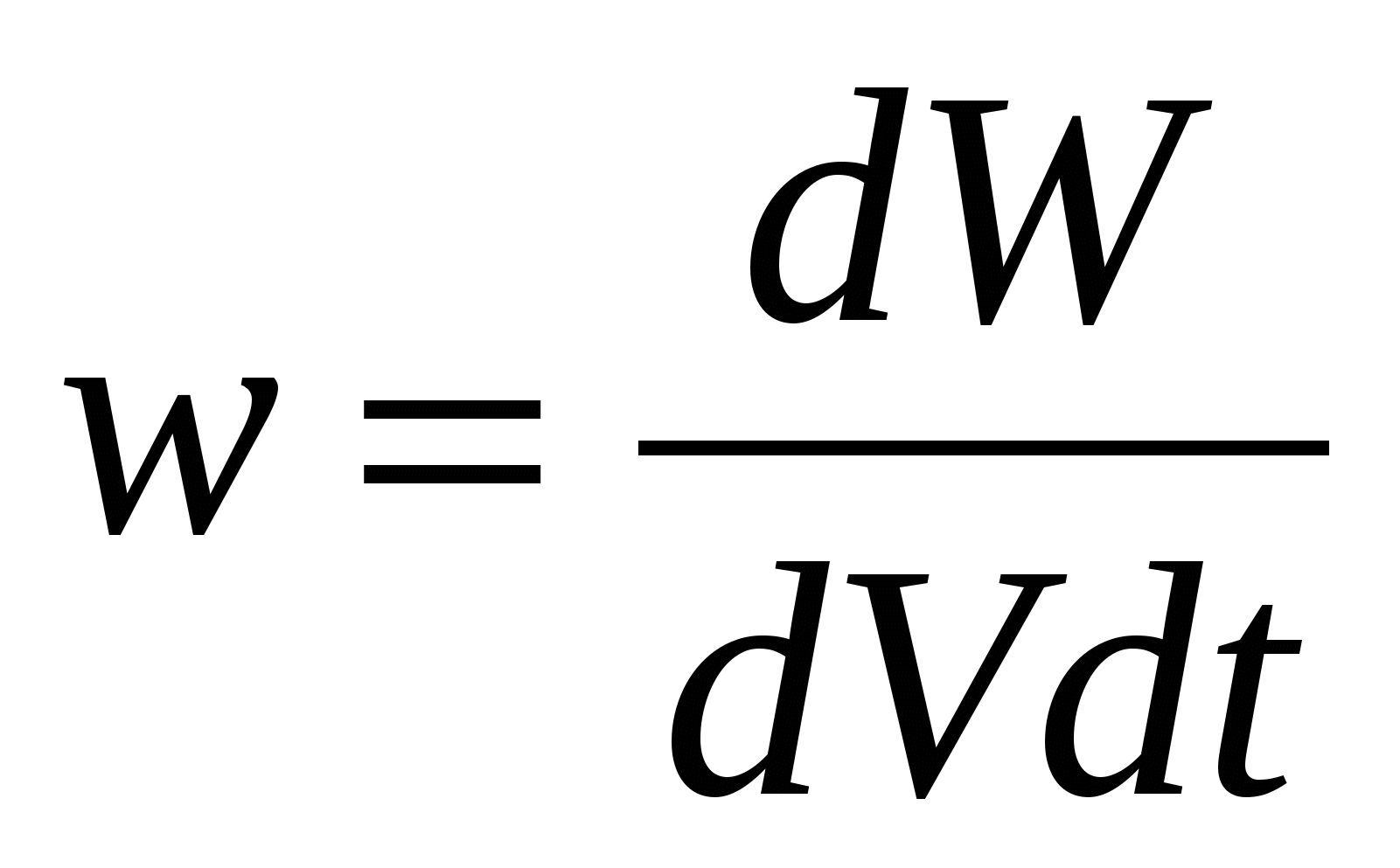 - определение удельной тепловой мощности тока; - определение удельной тепловой мощности тока;
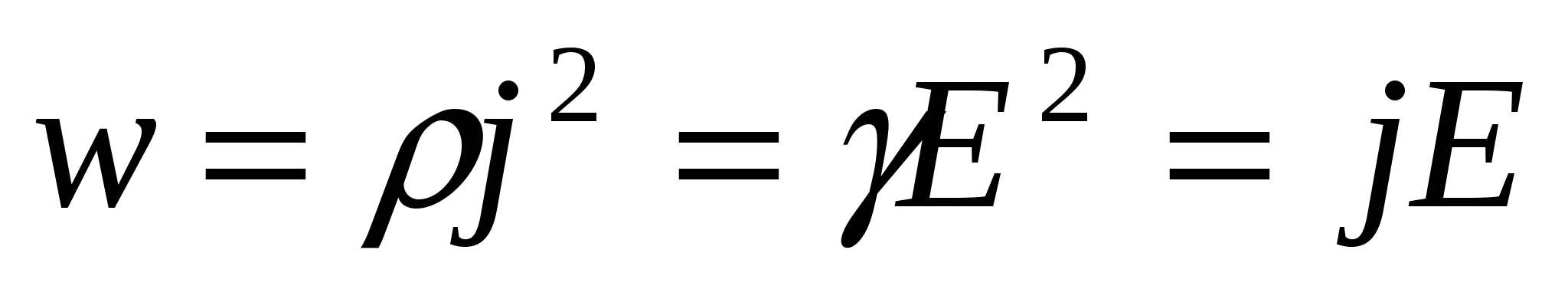 - закон Джоуля-Ленца в локальной форме. - закон Джоуля-Ленца в локальной форме.
12. Ток в жидкости и газе
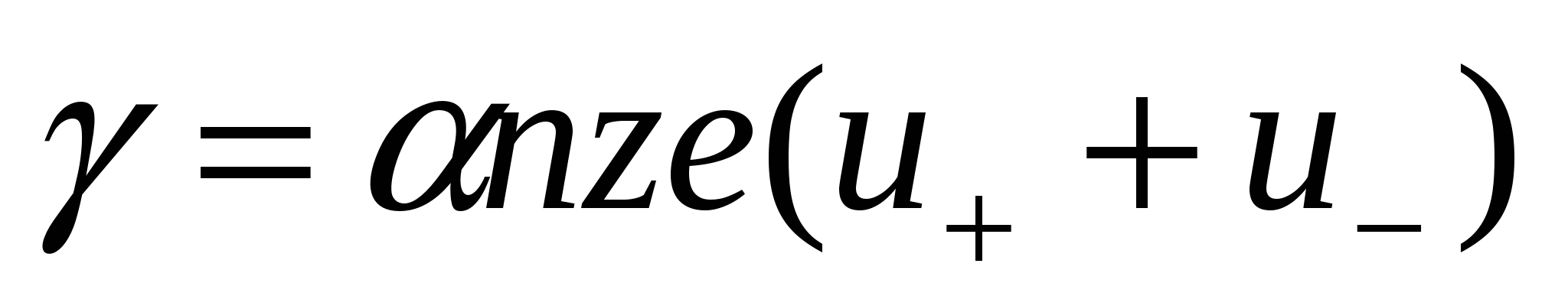 - удельная электропроводимость раствора электролита; - удельная электропроводимость раствора электролита;
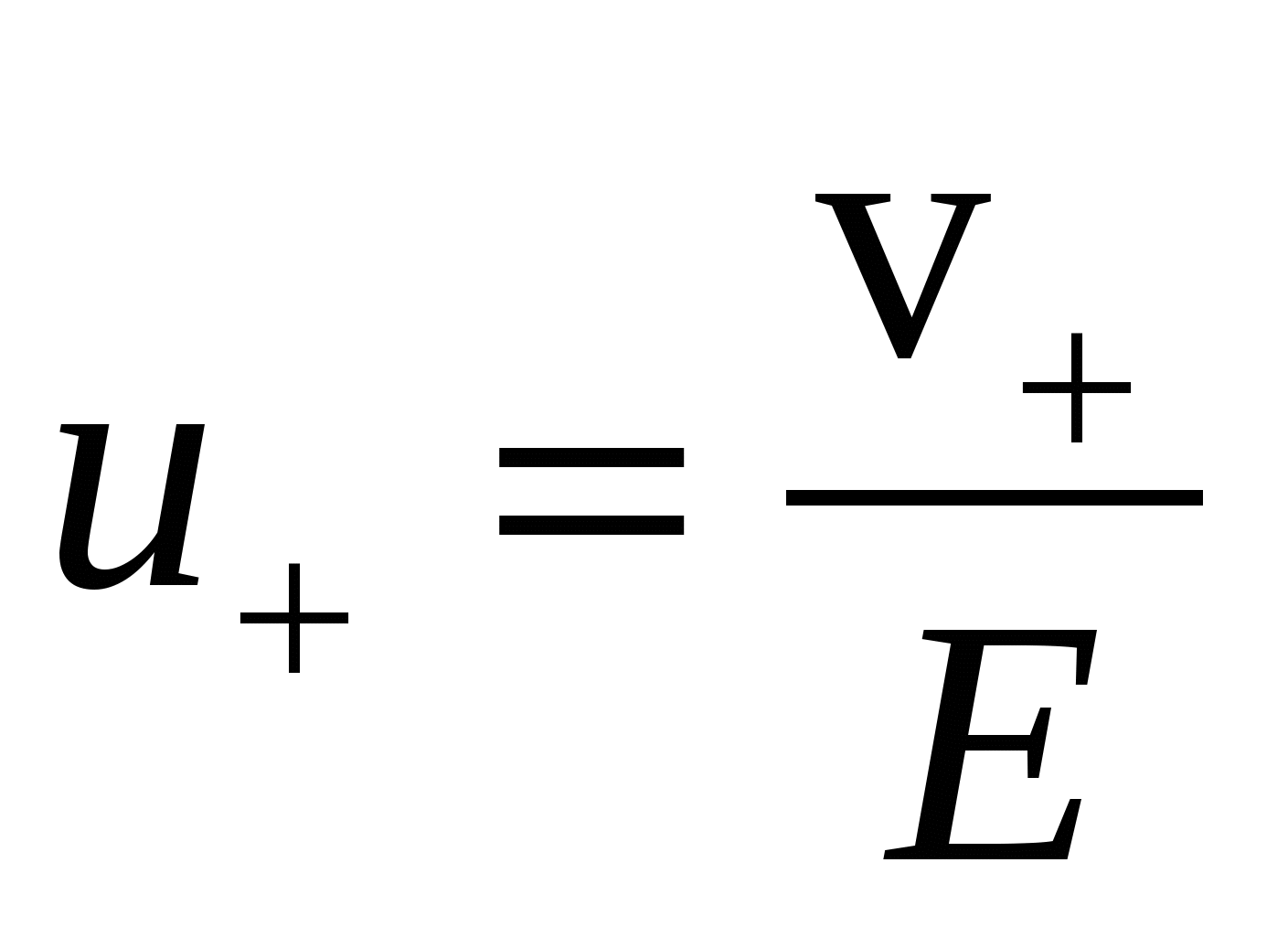 , , 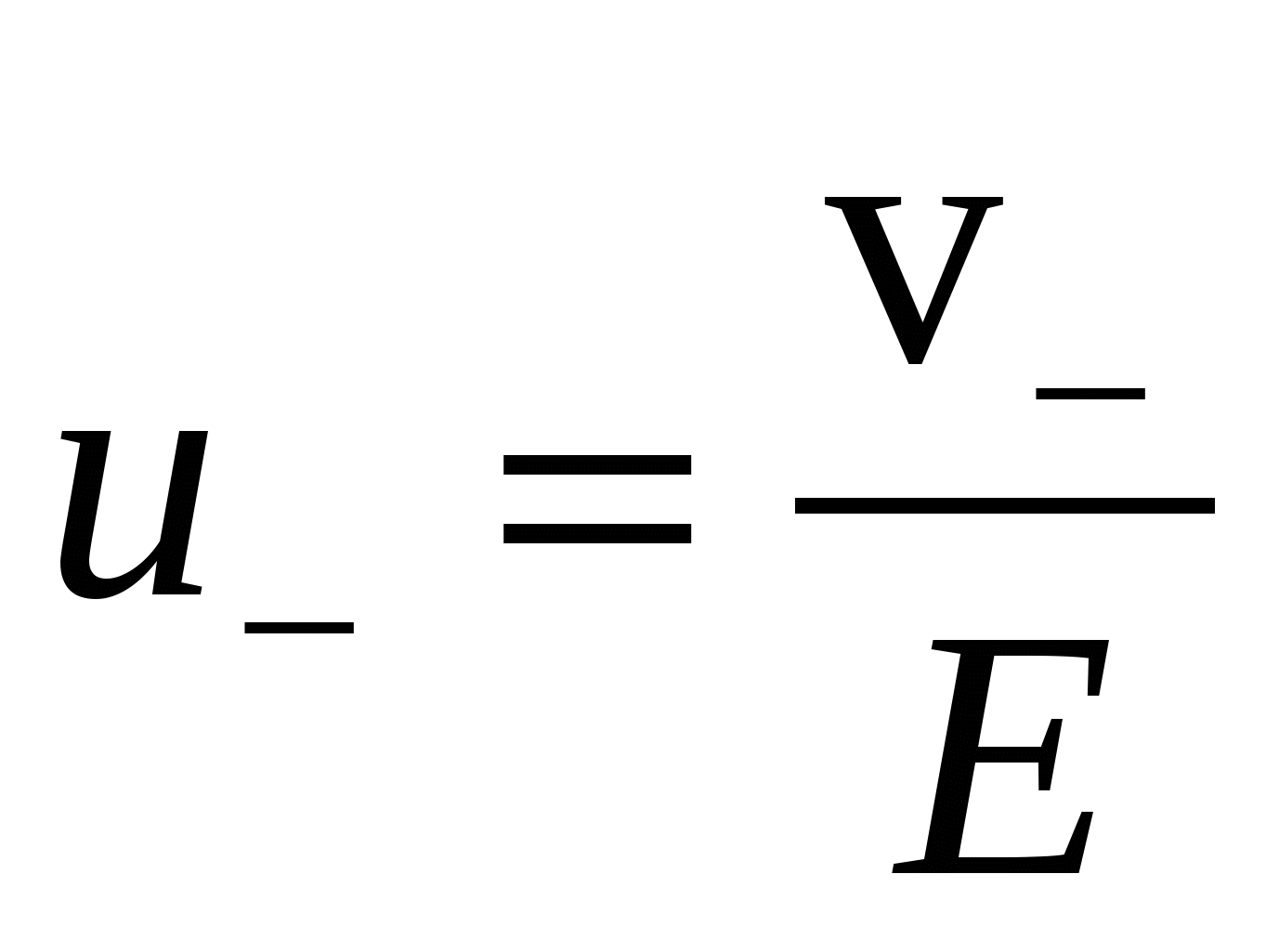 - подвижности ионов; - подвижности ионов;
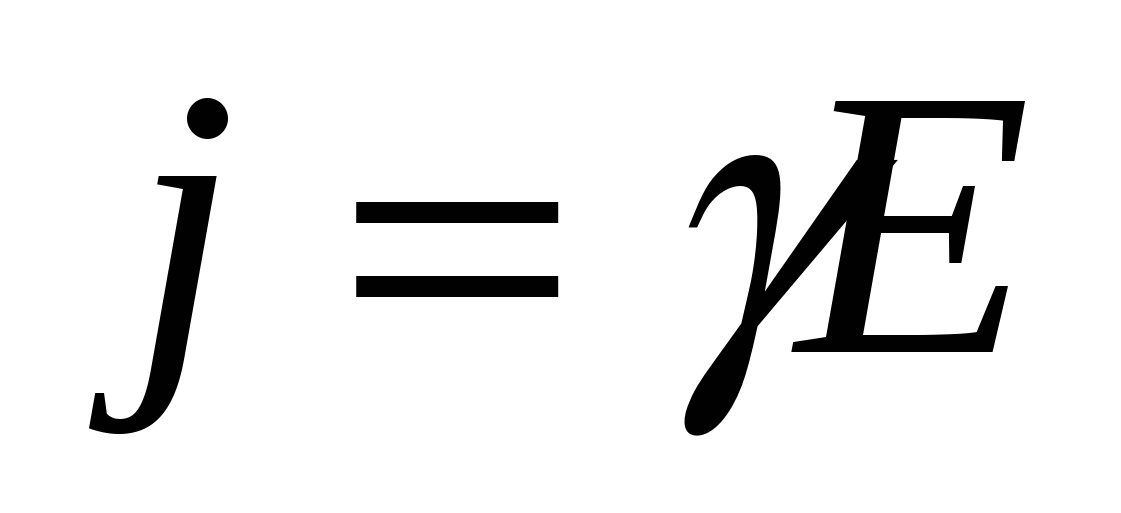 , - плотность тока, далекого от насыщения, в газе (закон Ома); , - плотность тока, далекого от насыщения, в газе (закон Ома);
 -удельная электропроводимость газа; -удельная электропроводимость газа;
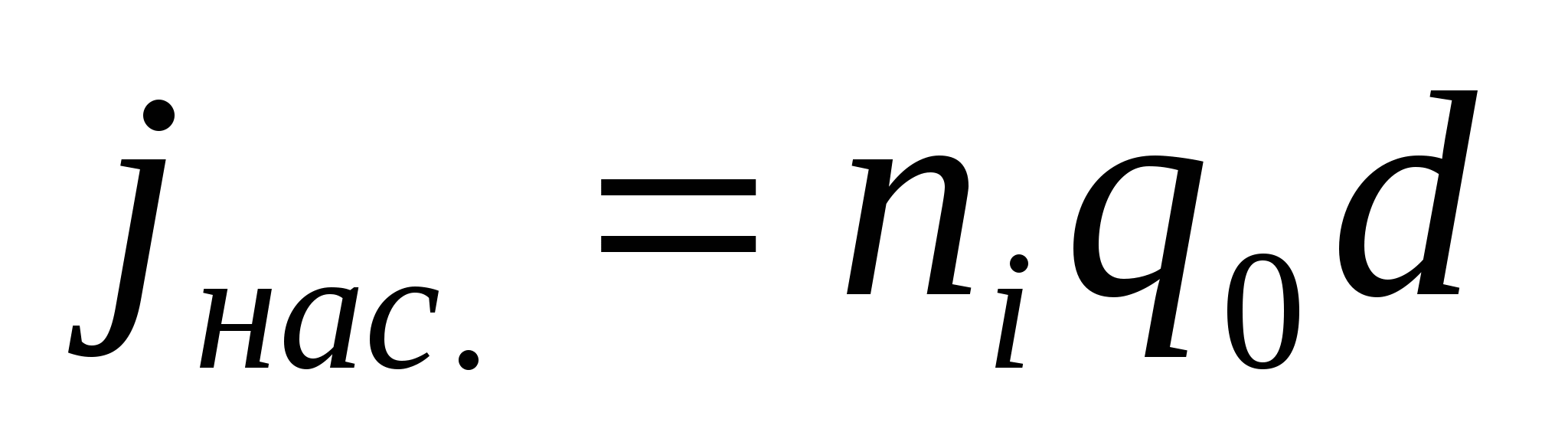 - плотность тока насыщения в газе. - плотность тока насыщения в газе.
13. Термоэлектронная эмиссия
 - плотность тока насыщения при термоэлектронной эмиссии (формула Ричардсона –Дешмена); - плотность тока насыщения при термоэлектронной эмиссии (формула Ричардсона –Дешмена);
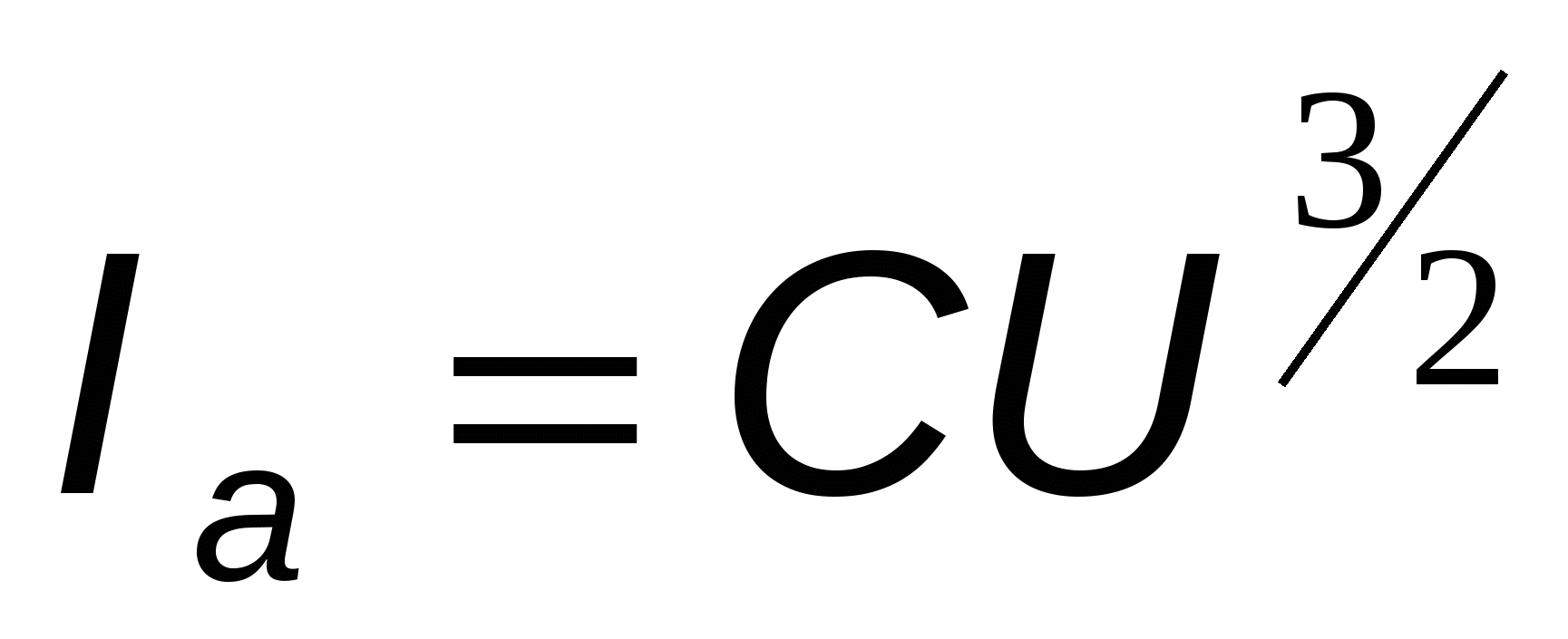 - закон «трех вторых» (Ленгмюра и Богуславского). - закон «трех вторых» (Ленгмюра и Богуславского).
Примеры решения задач.
Пример 1.
Определить напряжённость поля, создаваемого зарядом, равномерно распределённым по тонкому прямому стержню с линейной плотностью 200 нКл/м, в точке, лежащей на перпендикуляре, восстановленном в середине стержня, на расстоянии 40 см от его середины. Длина стержня 60 см.
Дано:
τ=2.10-7 Кл/м
l=0.6 м
b=0.4 м
|
Решение:
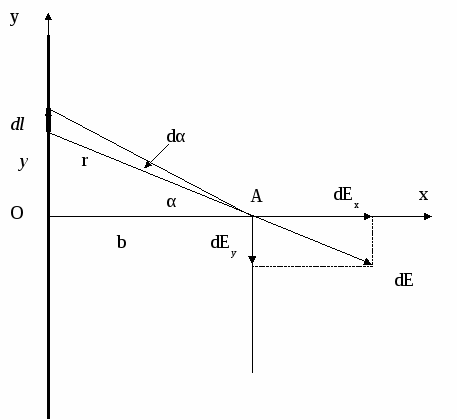
Разобьем стержень на бесконечно малые элементы dl=dy; y – координата данного элемента. Заряд элемента dq=τdy можно считать точечным. Напряженность поля, созданного зарядом dq в точке А на расстоянии r от заряда, равна:
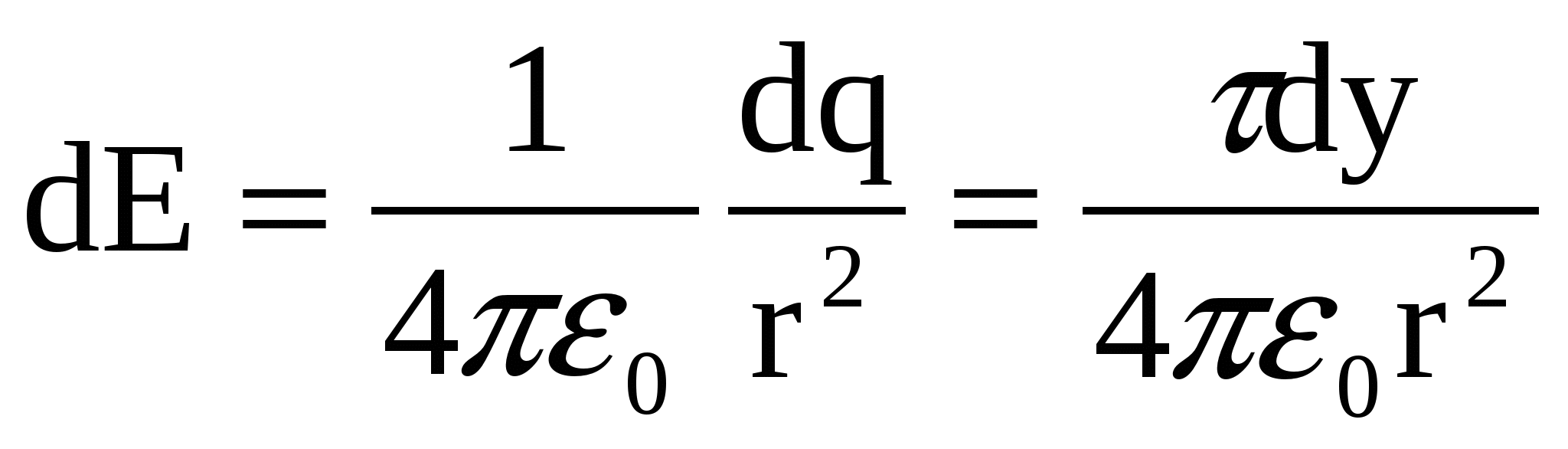 , (1) , (1)
где 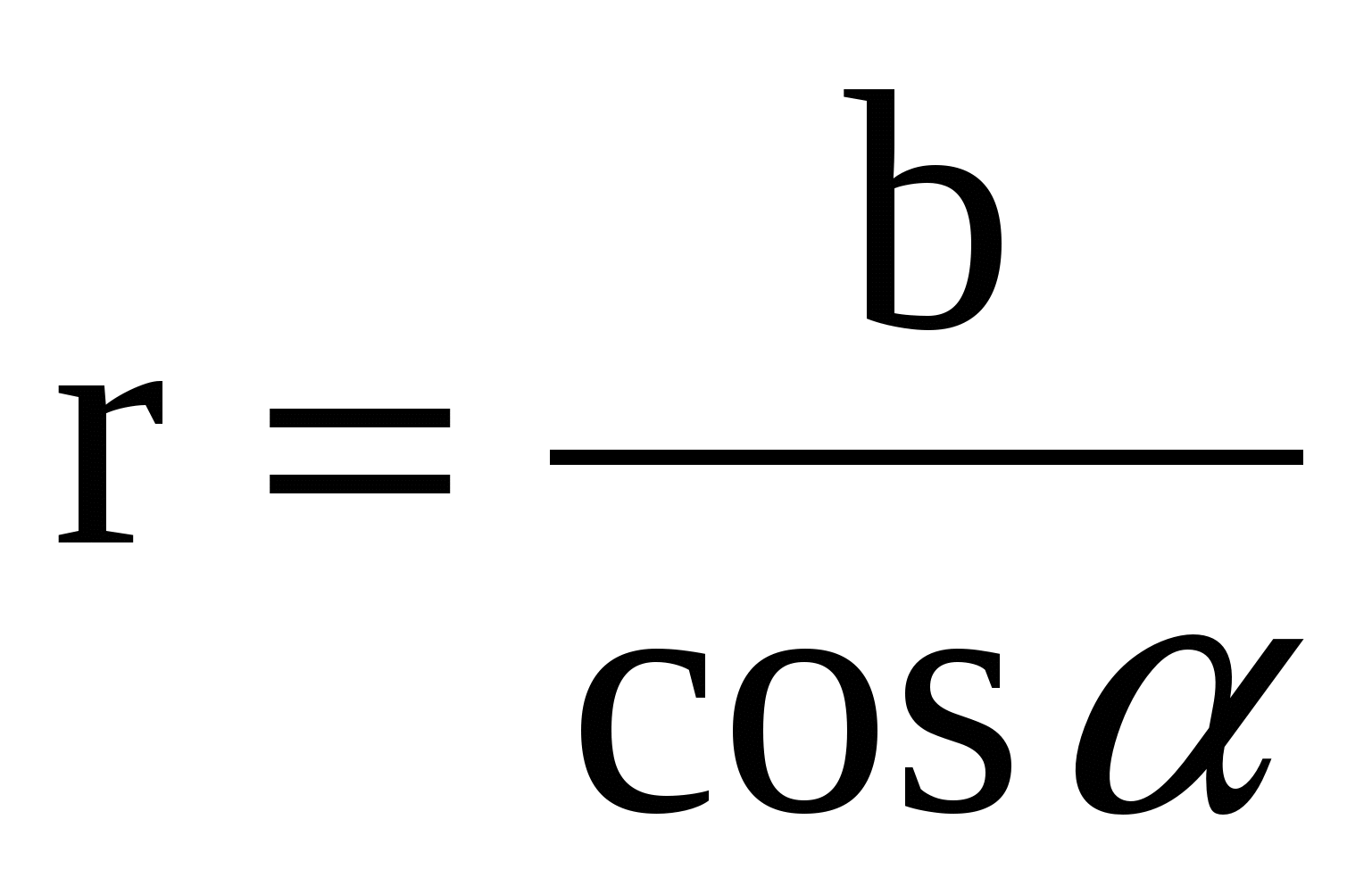 ; (2) ; (2) α – угол между перпендикуляром к стержню и радиус-вектором r элемента стержня, проведенным из точки А. Направление вектора напряженности см. на рисунке.
|
|
Найти:
Е=?
|
|
| Так как  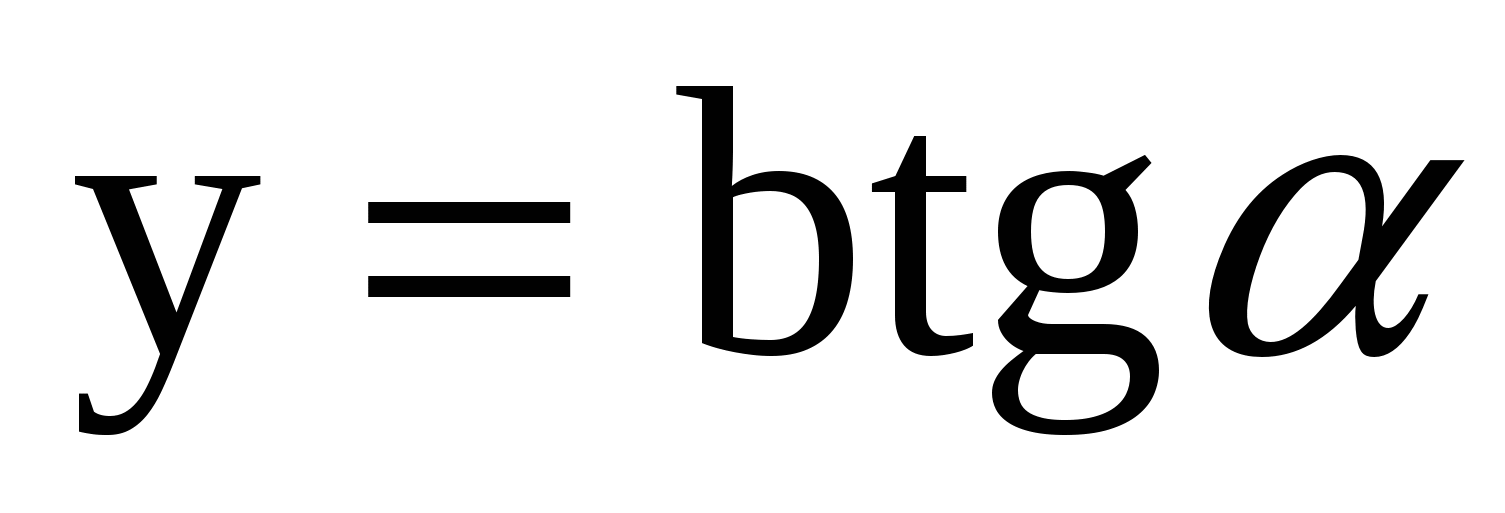 , , то то 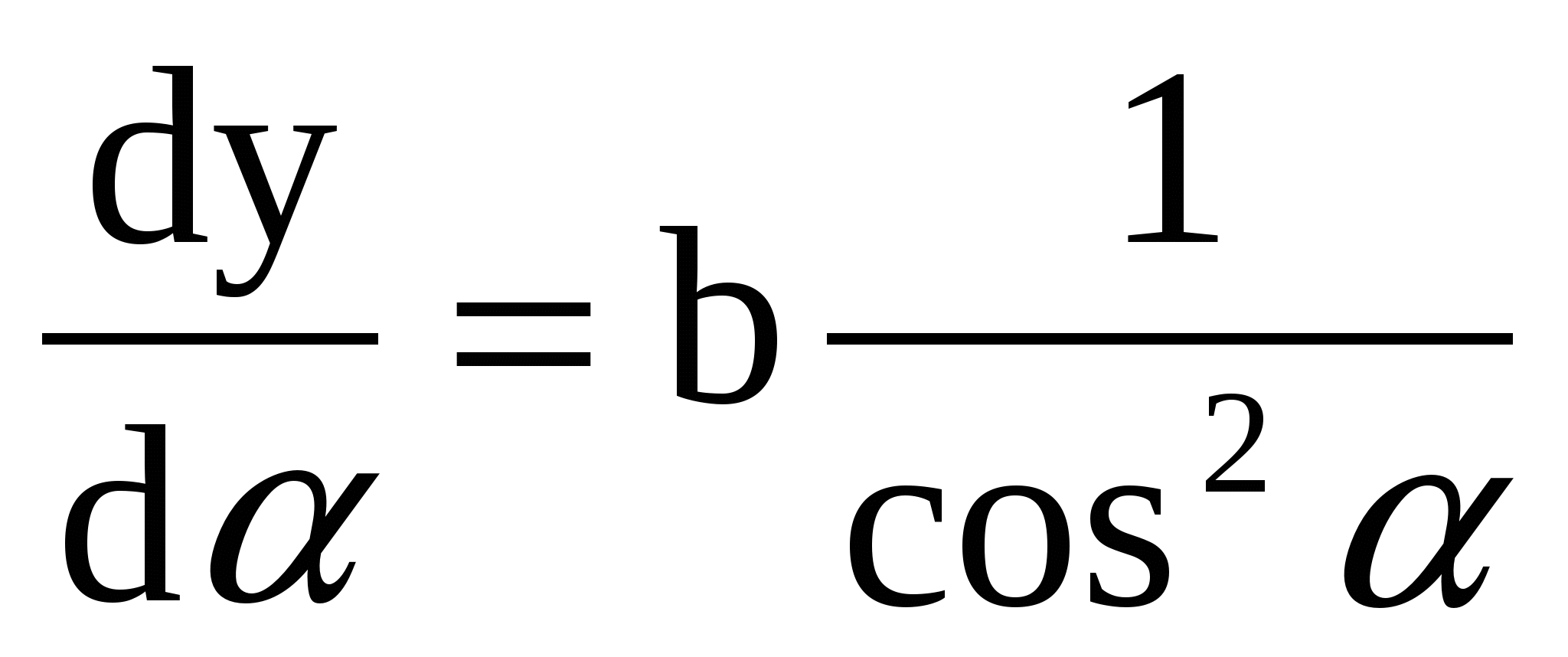 , или: , или:
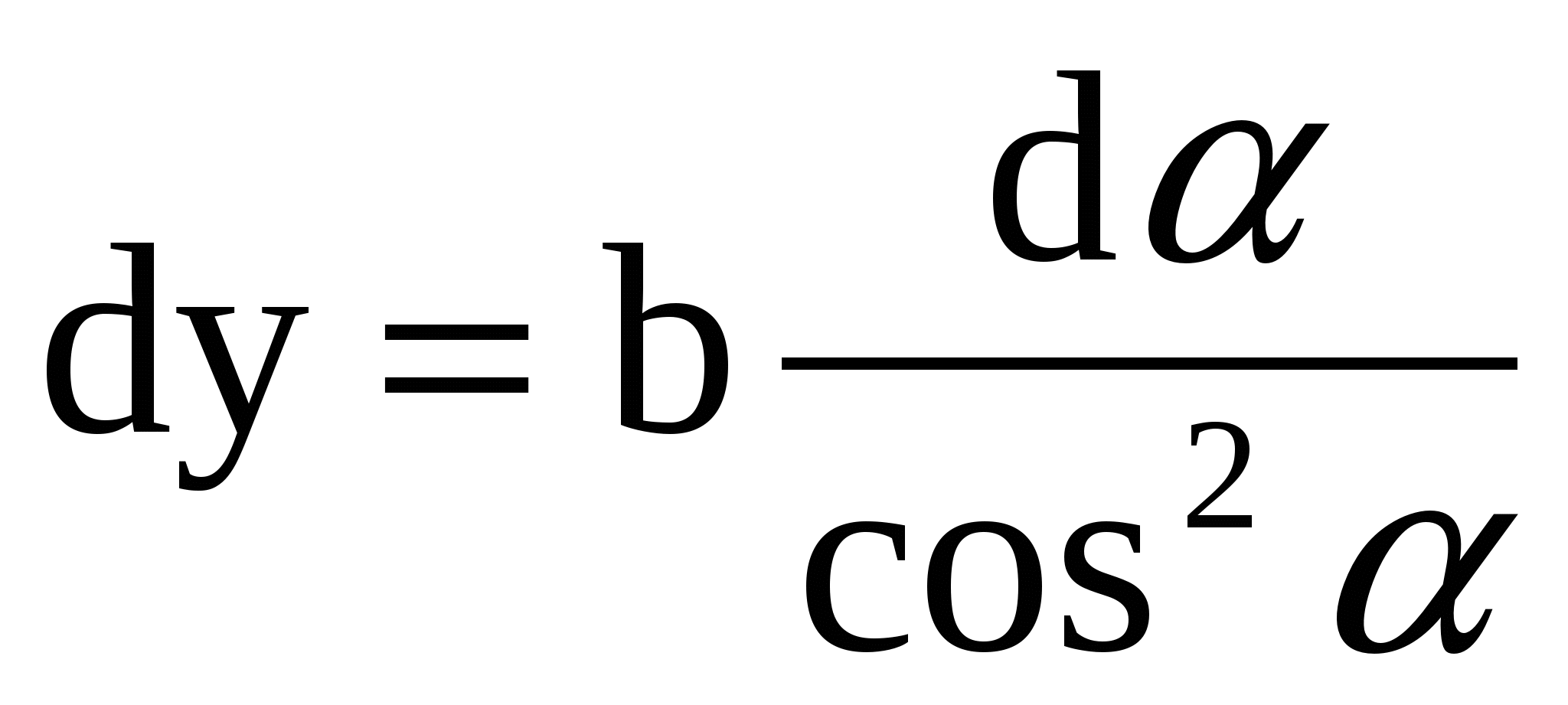 . (3) . (3)
Найдем проекции dE на координатные оси:
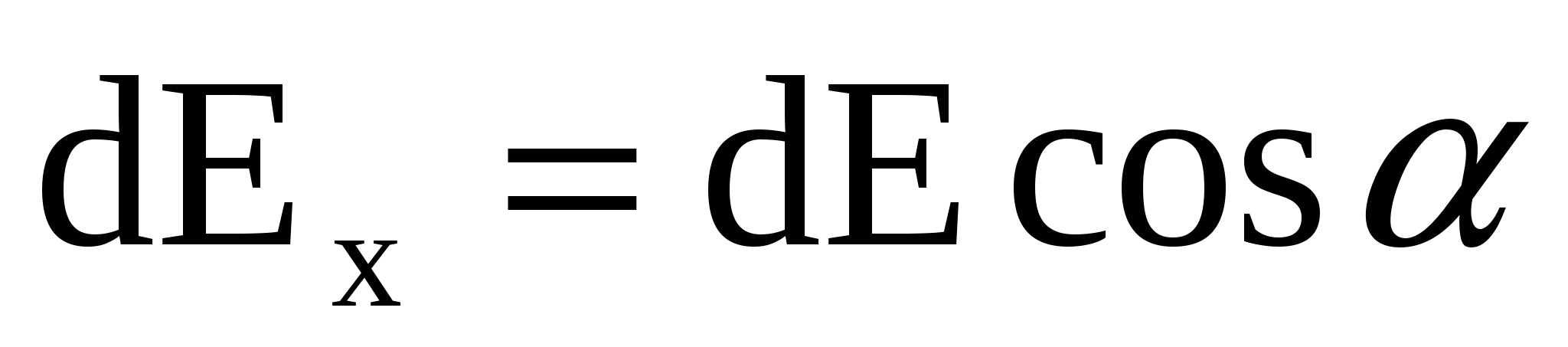 ; ; 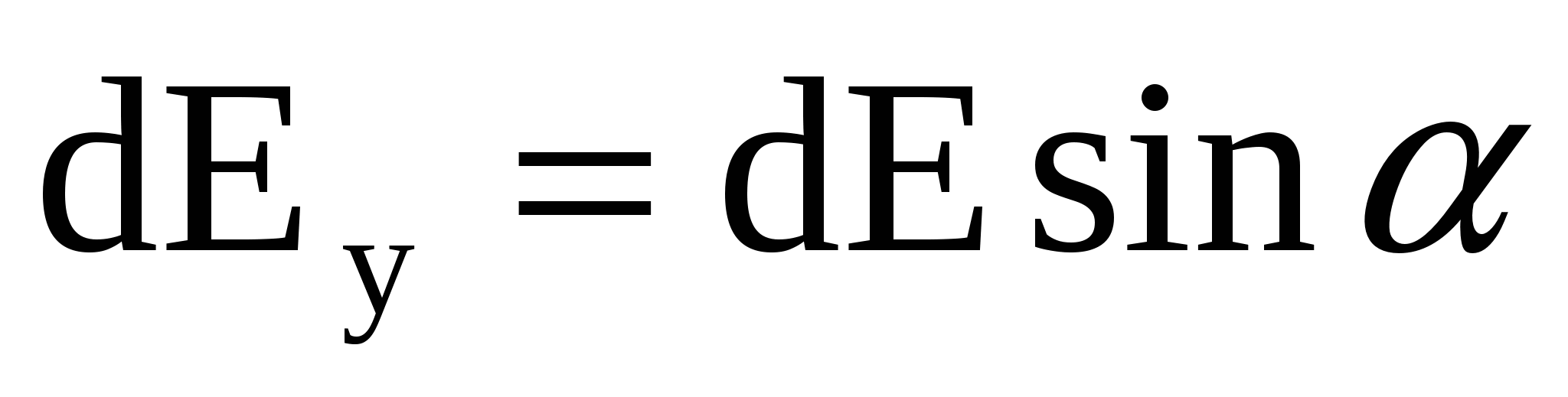 , (4) , (4)
Наконец, проекции полной напряженности на оси рассчитываются интегрированием:
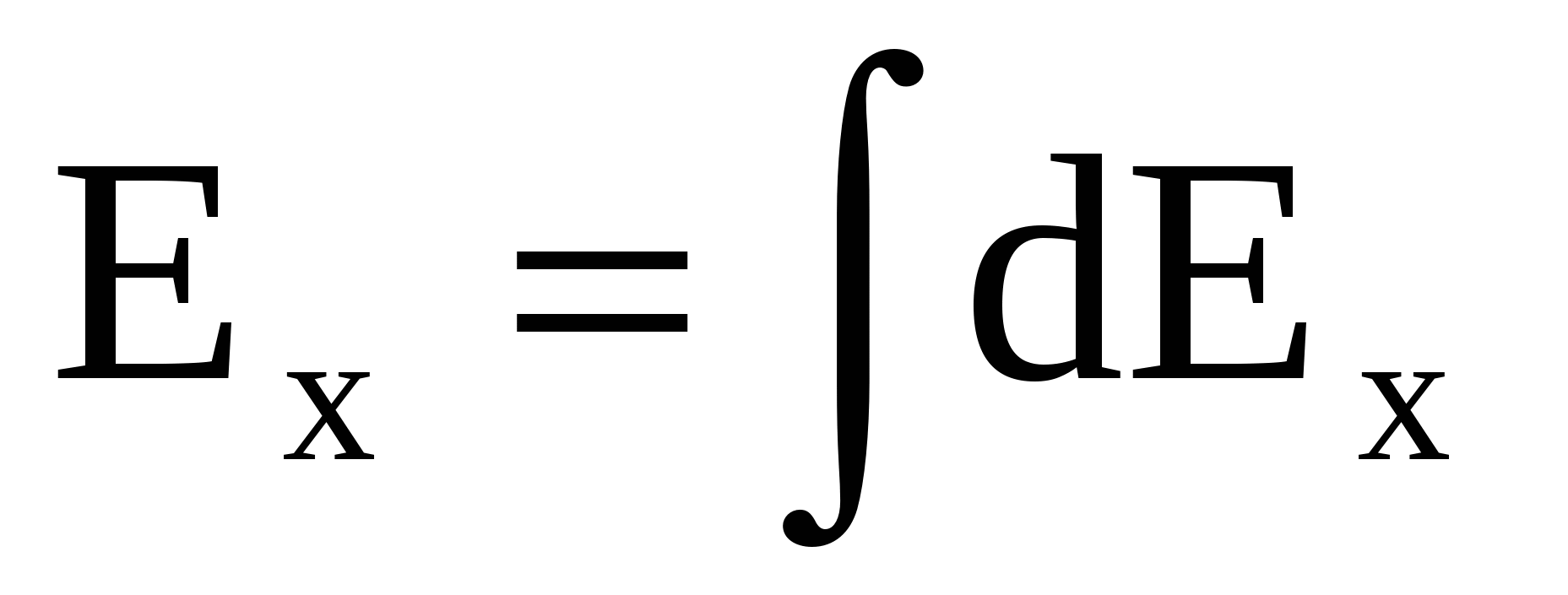 ; ; 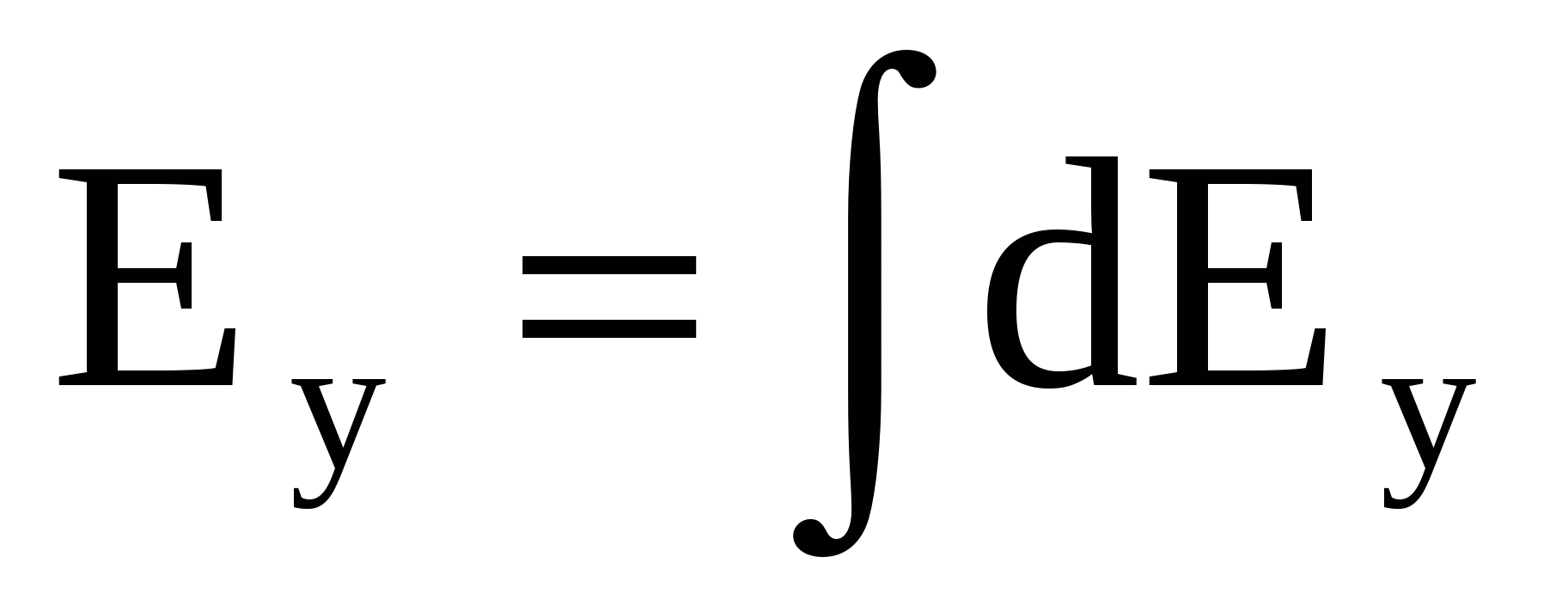 , (5) , (5)
причем интегрирование производится по всей длине стержня. Здесь использован принцип суперпозиции в проекциях на оси. Полная напряженность вычисляется по теореме Пифагора:
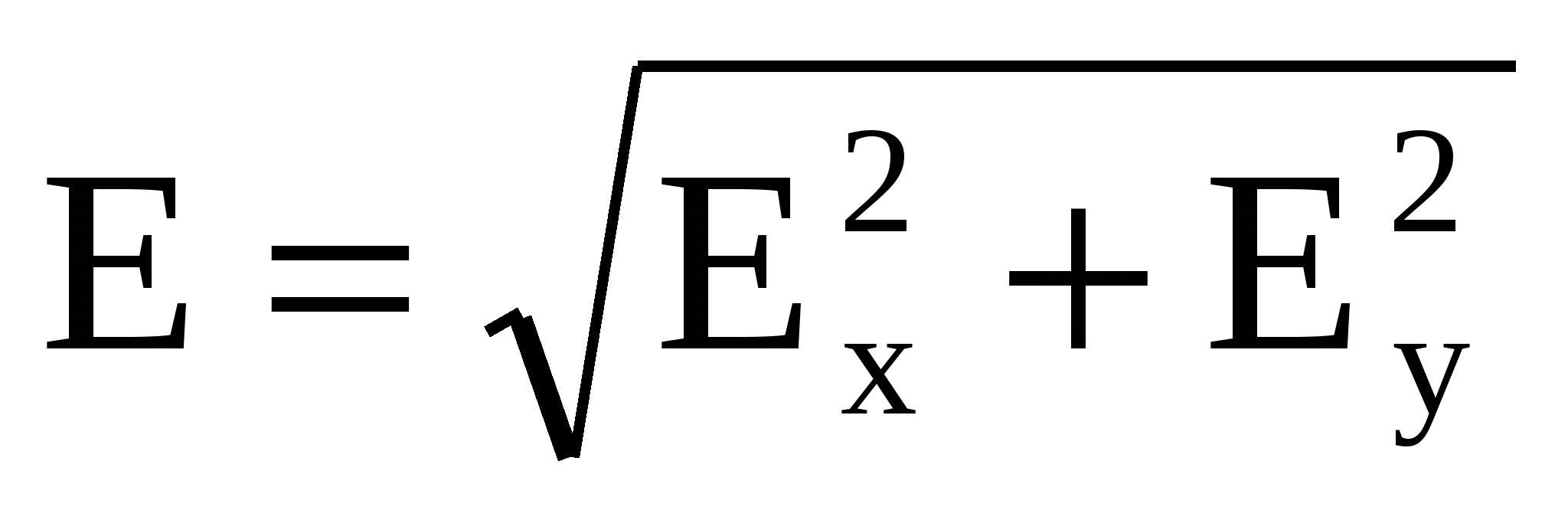 . (6) . (6)
С учетом (1) – (4) получим из (5):
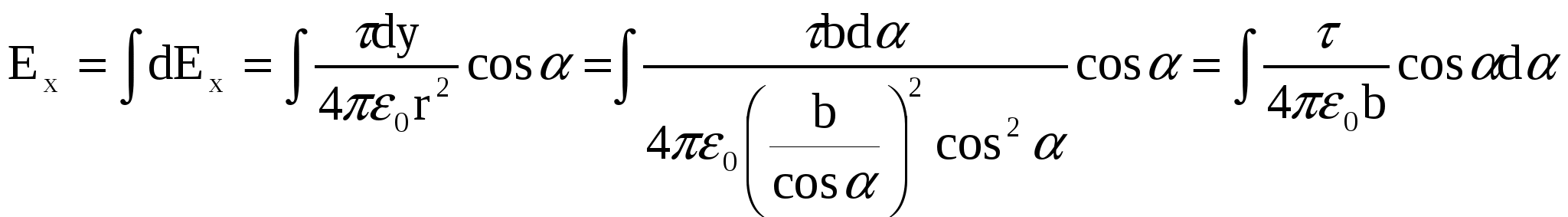 , (7) , (7)
 . .
Постоянную величину 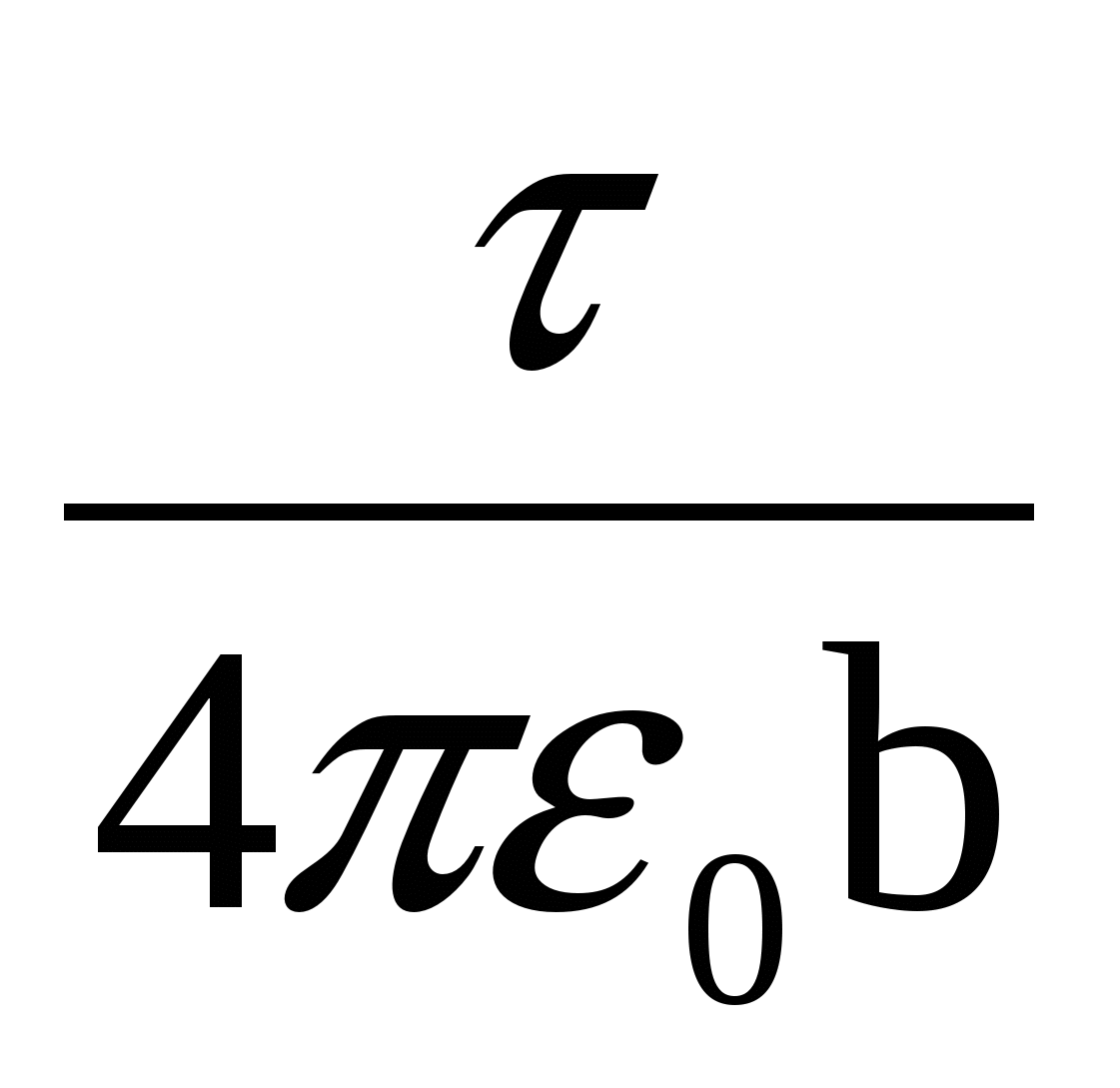 выносим за знак интеграла и проставим пределы интегрирования: угол α изменяется от (–α0) до α0, где выносим за знак интеграла и проставим пределы интегрирования: угол α изменяется от (–α0) до α0, где 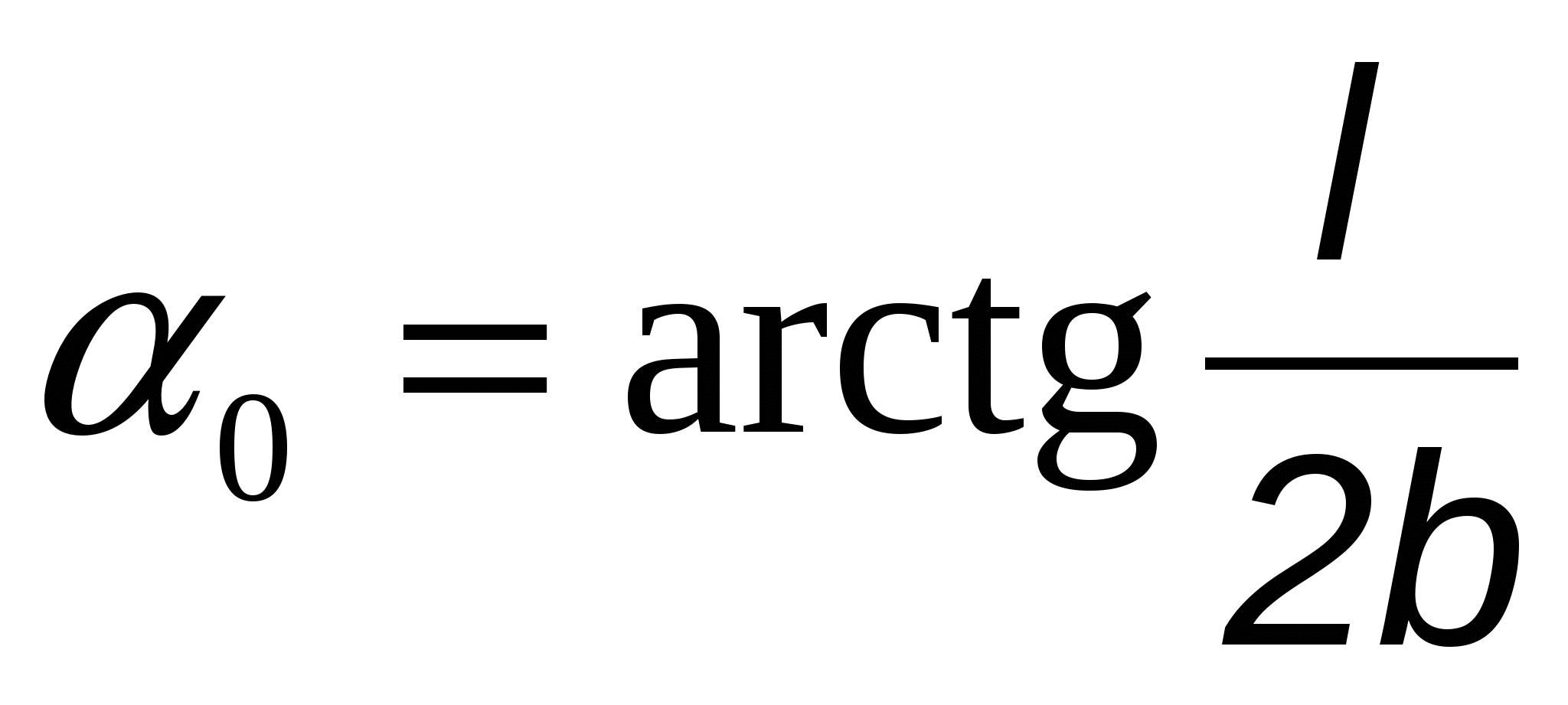 . Далее, первообразная функция от . Далее, первообразная функция от 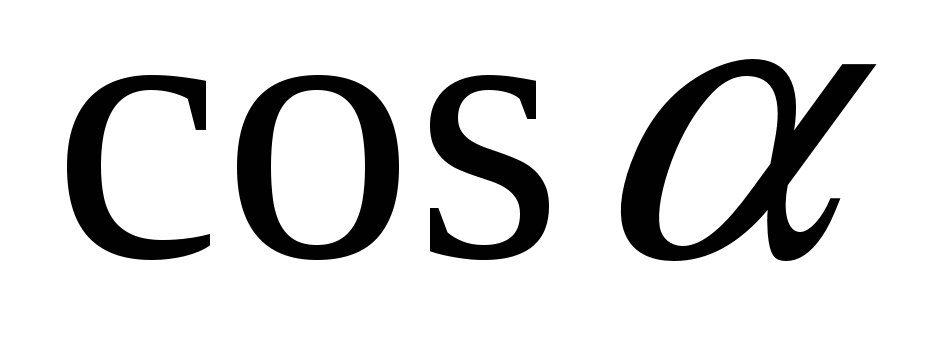 - это - это 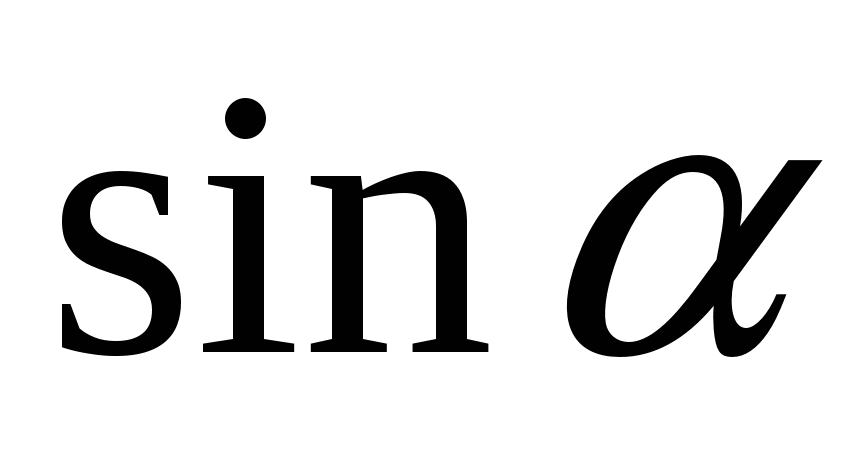 , а от , а от 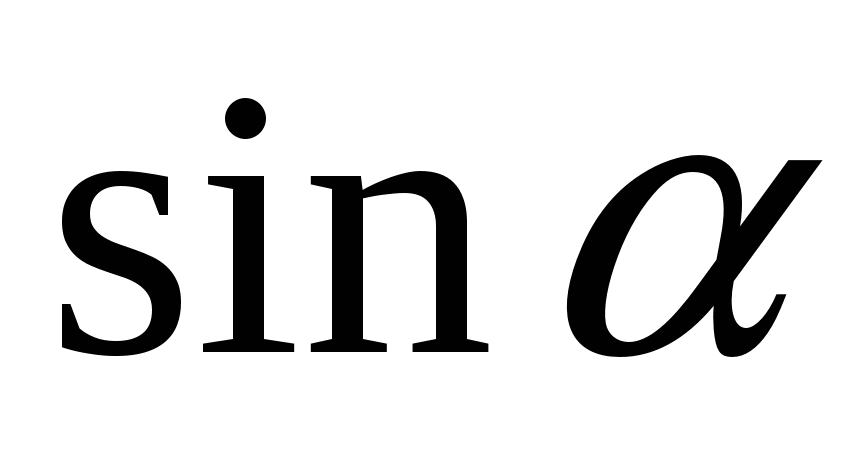 - -  . Тогда . Тогда
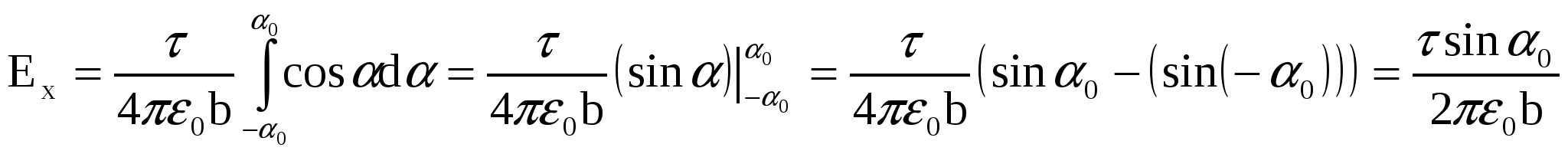 , ,
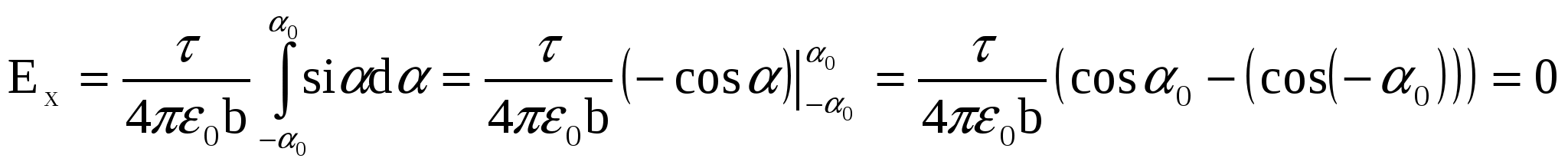 . .
Окончательно получаем для напряженности:
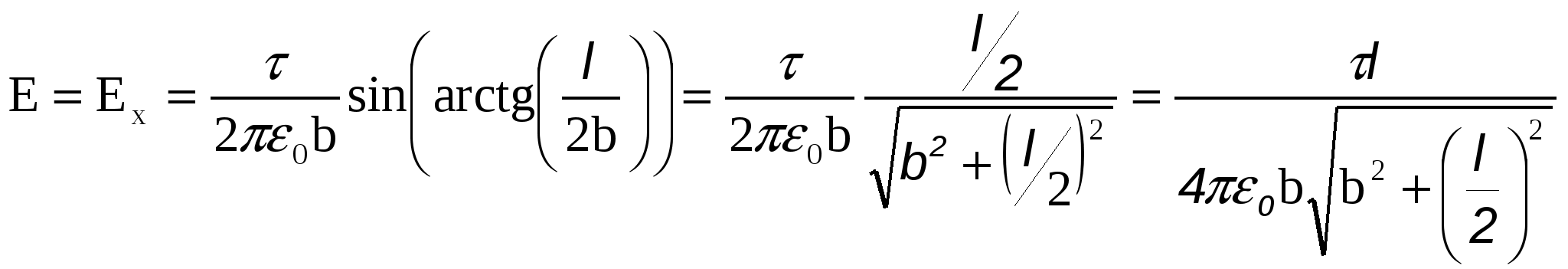 , ,
 . .
|
Ответ: E=5.4.103 В/м
|
Пример 2.
Определить потенциал поля, создаваемого зарядом, равномерно распределённым по тонкому прямому стержню с линейной плотностью 200 нКл/м, в точке, лежащей на перпендикуляре, восстановленном в одном из концов стержня, на расстоянии 40 см от него. Длина стержня 30 см.
Дано:
τ=2.10-7 Кл/м
l=0.3 м
b=0.4 м
|
Решение:
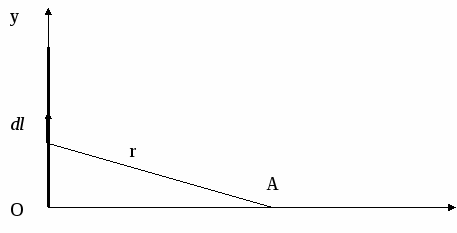
Разобьем стержень на бесконечно малые элементы dl=dy; y – координата данного элемента. Заряд элемента dq=τdy можно считать точечным. Потенциал поля, созданного зарядом dq в точке А на расстоянии r от заряда, равен:
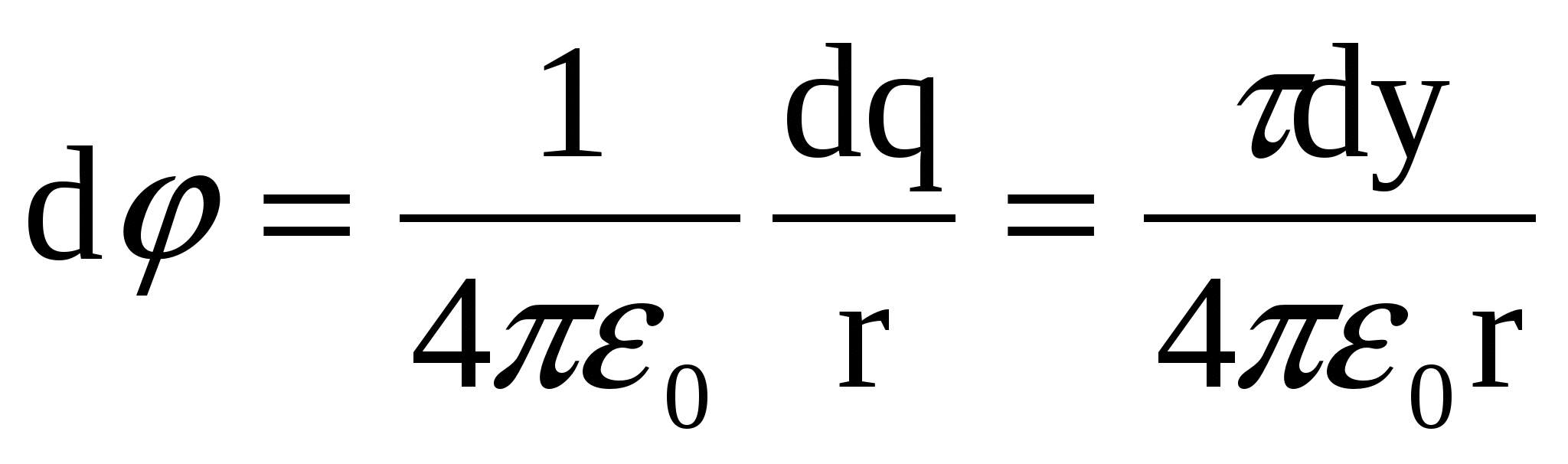 , (1) , (1)
где 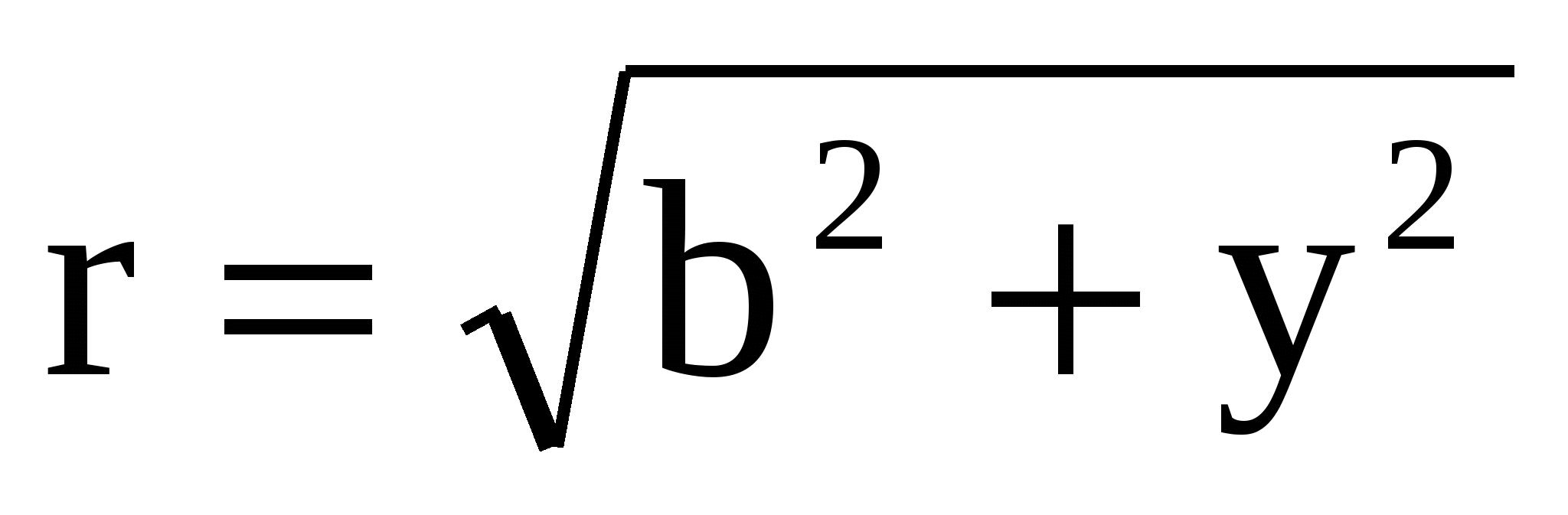 . (2) . (2) По принципу суперпозиции полный потенциал
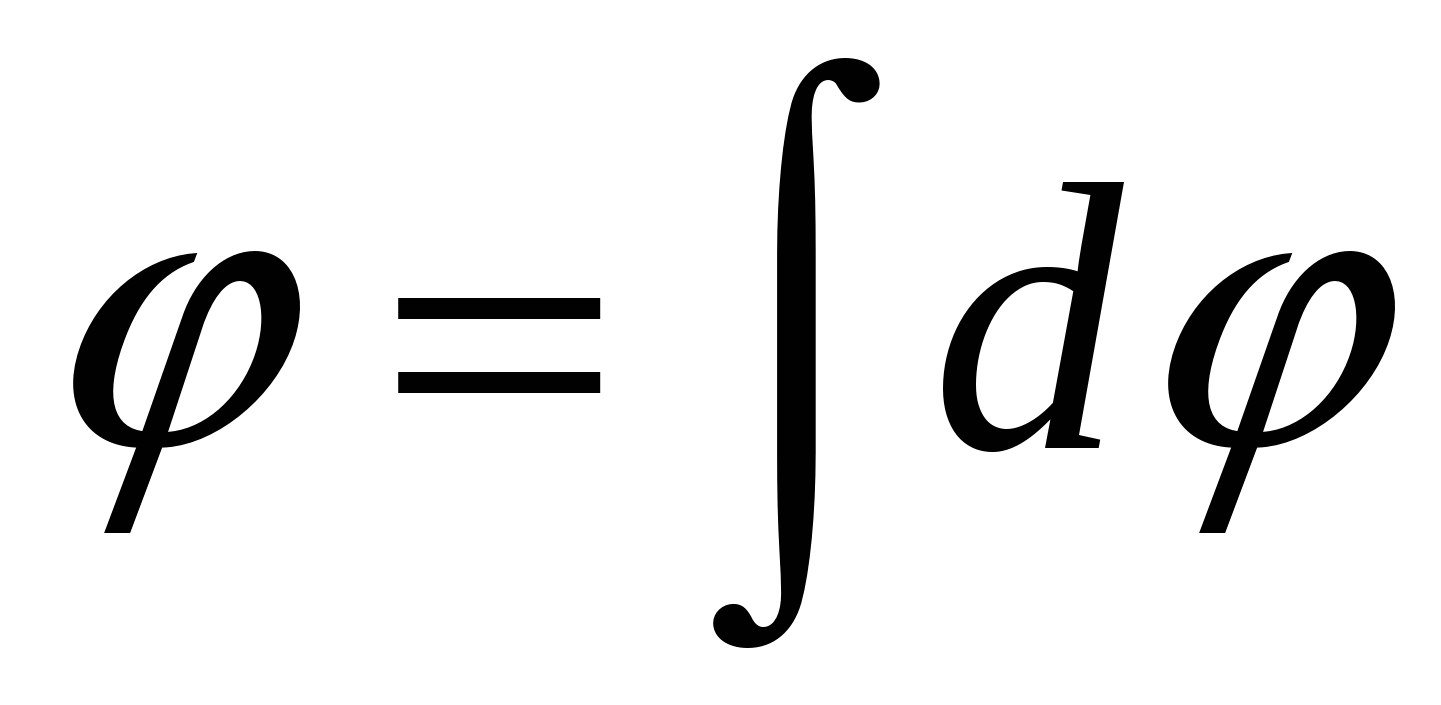 , (3) , (3)
где интегрирование ведется по всей длине стержня. Тогда
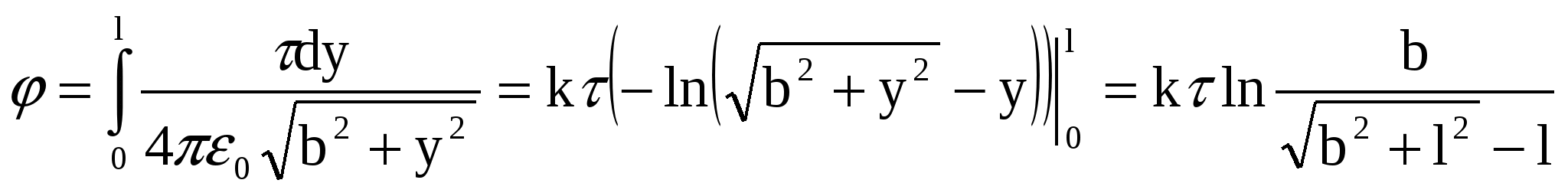 . (4) . (4)
Здесь  , константа , константа 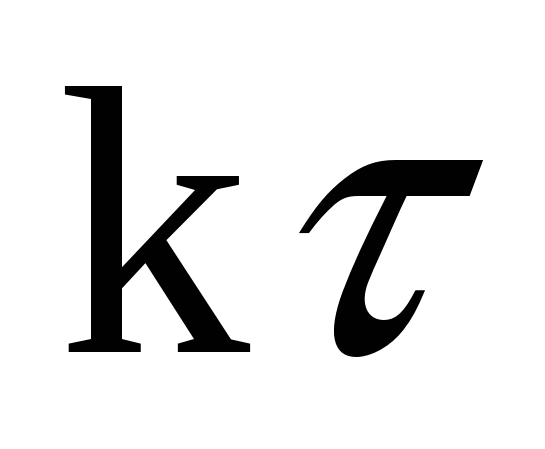 вынесена за знак интеграла и использовано, что первообразной функцией для функции вынесена за знак интеграла и использовано, что первообразной функцией для функции 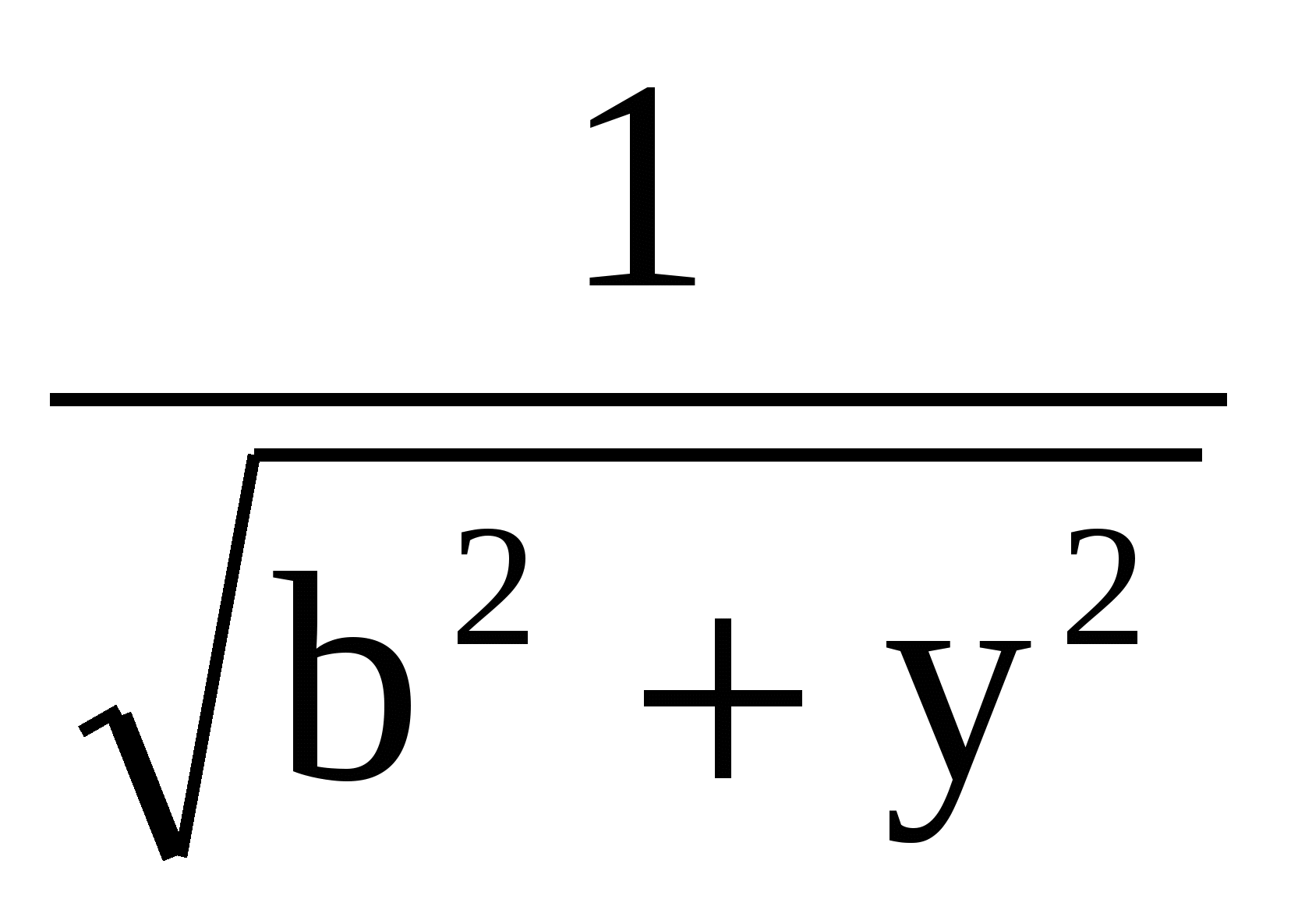 является является 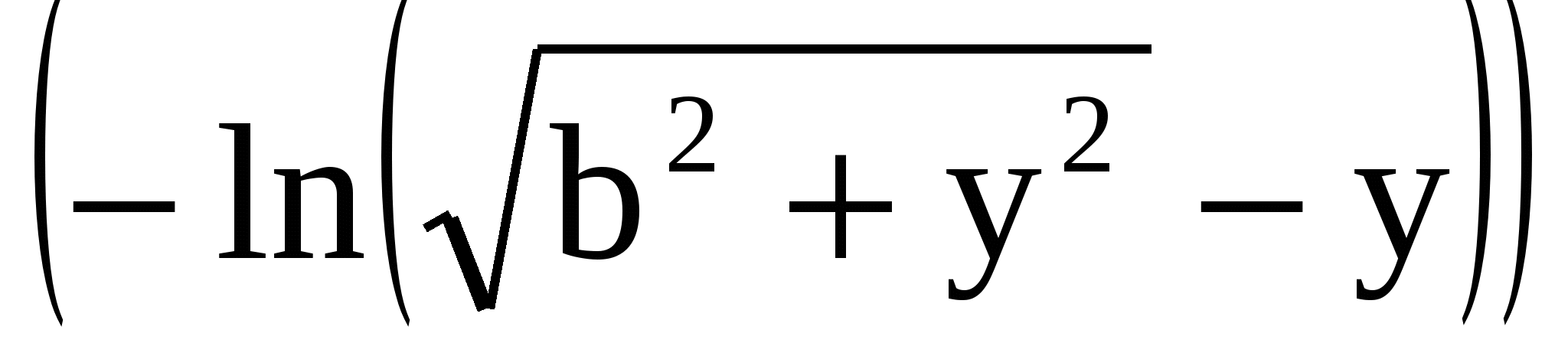 , в чем можно убедиться дифференцированием: , в чем можно убедиться дифференцированием:
|
Найти:
φ=?
|
| 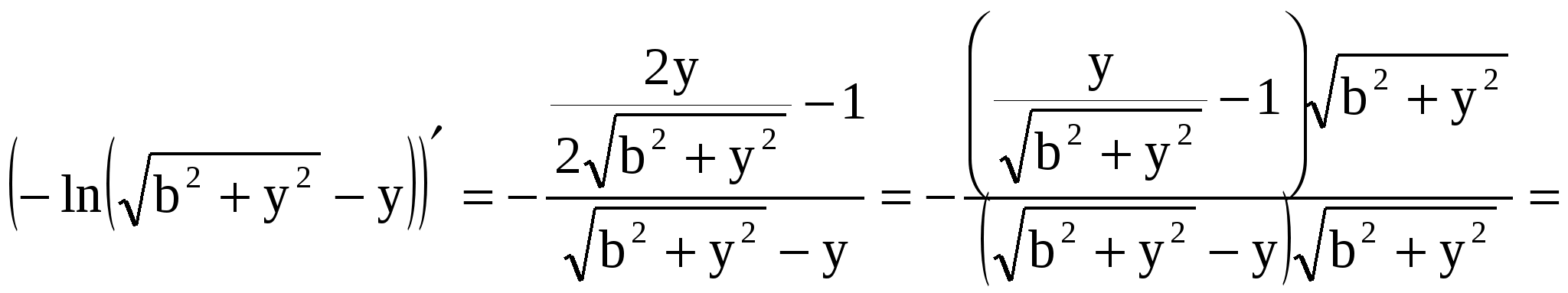
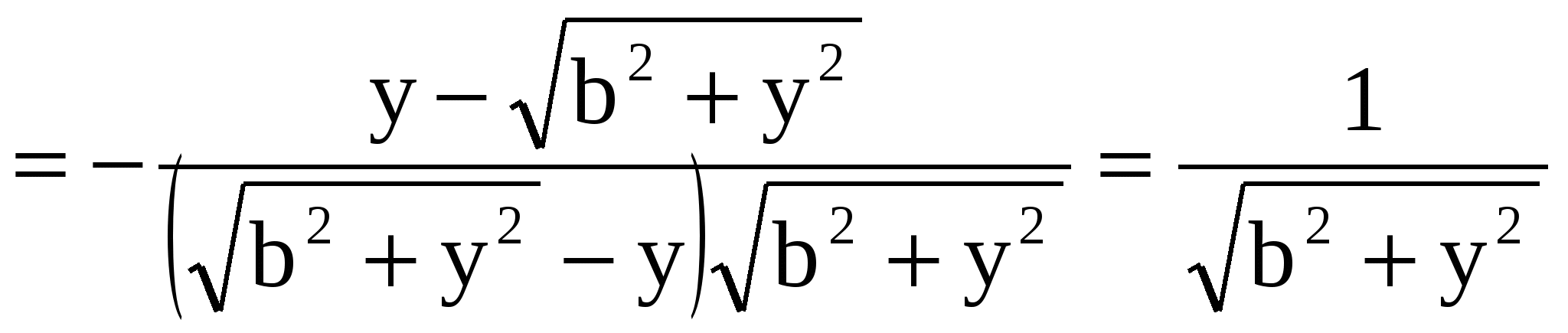
По формуле (4) вычисляем потенциал:
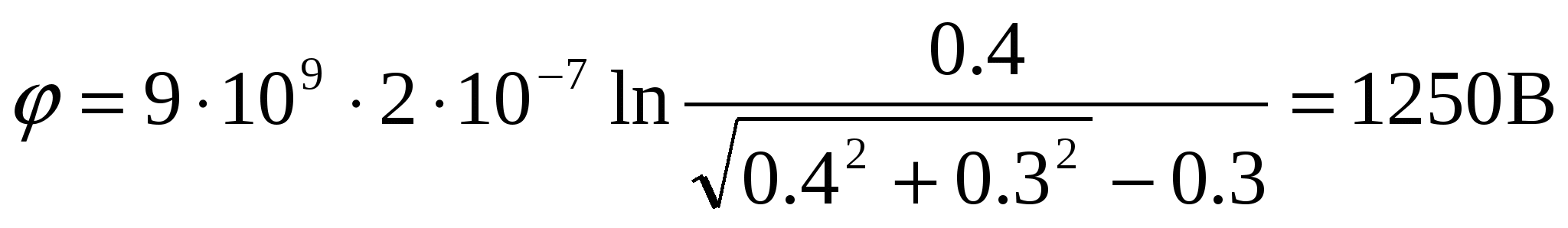
|
Ответ: φ=1250 В
|
Пример 3.
На двух коаксиальных бесконечных цилиндрах радиусами 5 см и 10 см равномерно распределены заряды с линейными плотностями заряда τ1=100 нКл/м и τ2=50 нКл/м соответственно. Пространство между цилиндрами заполнено парафином с диэлектрической проницаемостью 2. Найти напряженность электрического поля в точках, удаленных от оси цилиндров на расстояния 3 см, 9 см, 15 см.
Дано:
τ1=100 нКл/м
τ2=50 нКл/м
R1=0.05 м
R2=0.1 м
r1=0.03 м
r2=0.09 м
r3=0.15 м
ε=2
|
Решение:


|
Найти:
E1=?
E2=?
E3=?
|
|
Симметрия задачи позволяет воспользоваться теоремой Гаусса: поток вектора напряженность электростатического поля через любую замкнутую поверхность равен сумме свободных зарядов, охваченных этой поверхностью, деленной на (εε0):
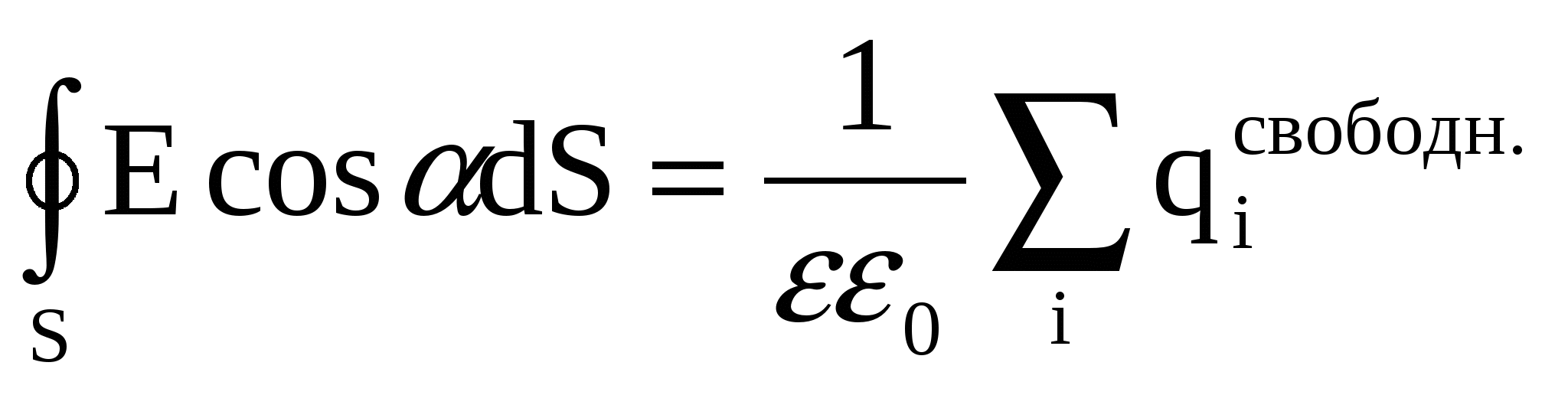 . (1) . (1)
здесь α – угол между вектором 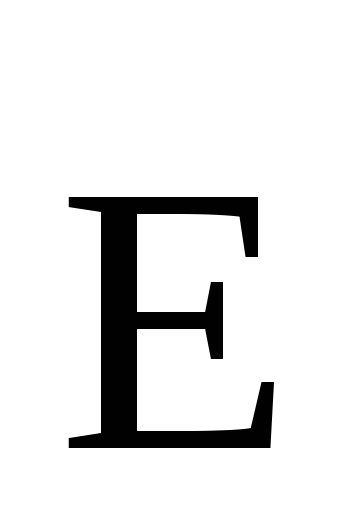 и нормалью к поверхности в данной точке. Возьмем Гауссову поверхность в виде цилиндра, коаксиального данным, высота которого равна h, а радиус r. Вектор и нормалью к поверхности в данной точке. Возьмем Гауссову поверхность в виде цилиндра, коаксиального данным, высота которого равна h, а радиус r. Вектор 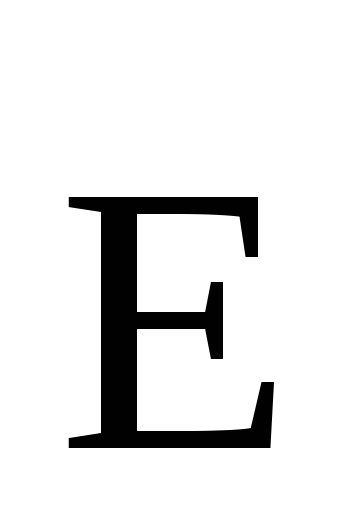 напряженности электростатического поля может быть направлен только перпендикулярно боковой поверхности цилиндра, параллельно основаниям, (см. рис.), тогда в левой части (1) надо учитывать только вклад через боковую поверхность цилиндра (для оснований α=900, cosα=0), причем для боковой поверхности α=0, cosα=1. Кроме того, в силу симметрии значение напряженности в любой точке боковой поверхности Гауссова цилиндра одинаково, и значение Е можно вынести за знак интеграла. Тогда напряженности электростатического поля может быть направлен только перпендикулярно боковой поверхности цилиндра, параллельно основаниям, (см. рис.), тогда в левой части (1) надо учитывать только вклад через боковую поверхность цилиндра (для оснований α=900, cosα=0), причем для боковой поверхности α=0, cosα=1. Кроме того, в силу симметрии значение напряженности в любой точке боковой поверхности Гауссова цилиндра одинаково, и значение Е можно вынести за знак интеграла. Тогда
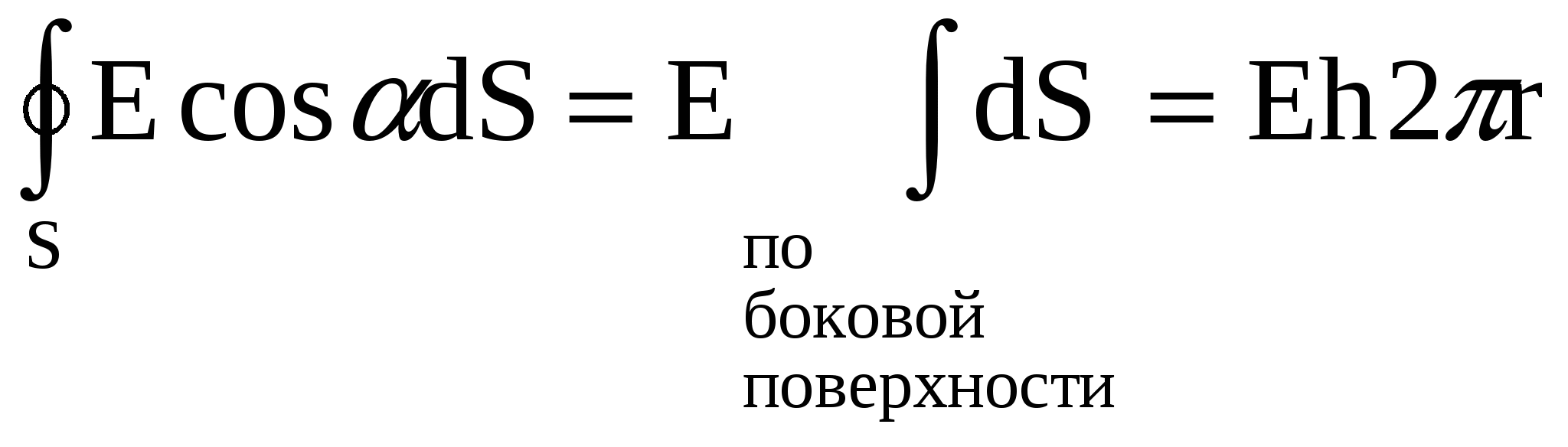 , (2) , (2)
где 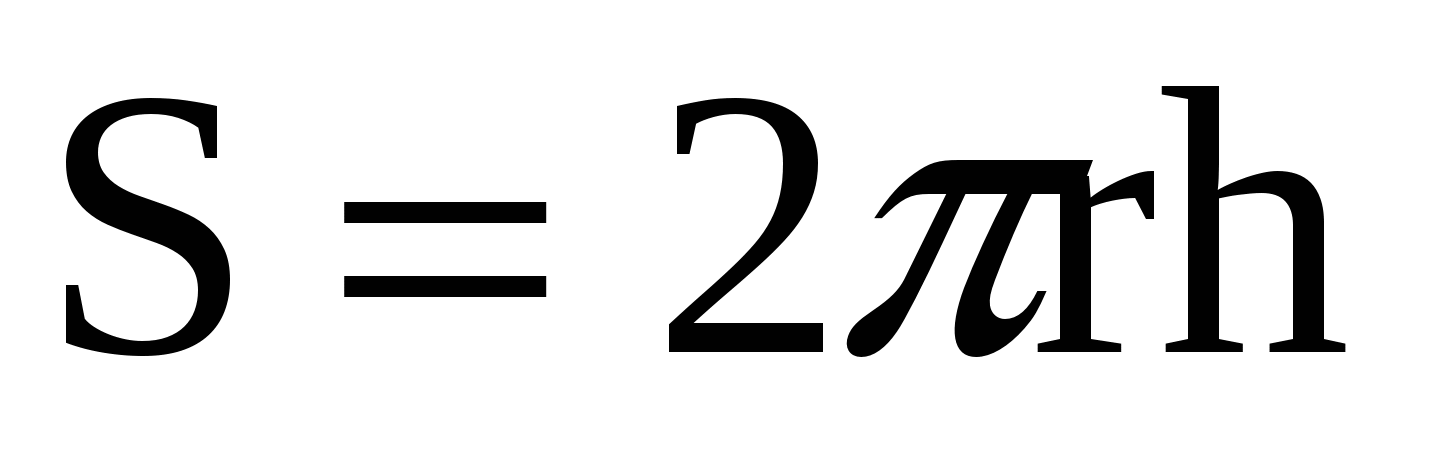 - площадь боковой поверхности Гауссова цилиндра. - площадь боковой поверхности Гауссова цилиндра.
Теперь вычислим правую часть (1). При этом нужно рассмотреть 3 случая:
1) r11. В этом случае внутрь Гауссовой поверхности не попадают заряды (q=0), и тогда из (1) и (2) следует, что E1=0.
2) R122. Внутрь Гауссовой поверхности попадают заряды, находящиеся только на внутреннем цилиндре радиуса R1 (см. рис.), поэтому суммарный заряд (по определению линейной плотности заряда):
q=τ1h. (3)
Из (1) – (3) получим:  , откуда , откуда
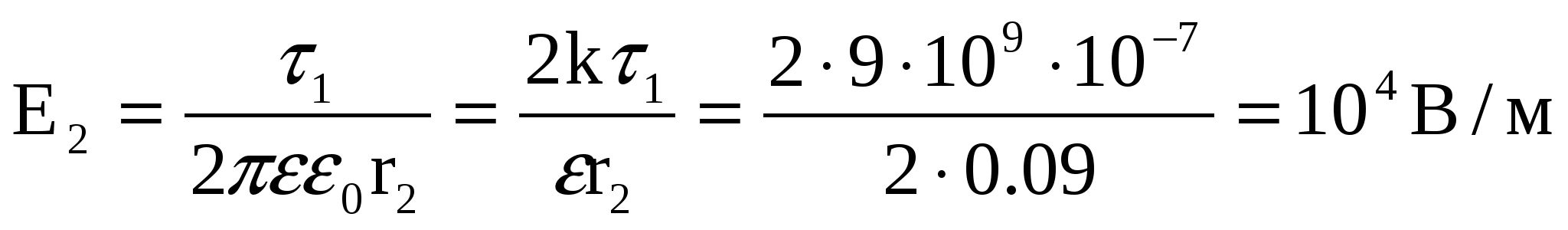 . .
Здесь сделана замена  . .
|
|
3) R23. Теперь Гауссова поверхность охватывает оба цилиндра, несущие свободные заряды с линейными плотностями τ1 и τ2, но при этом она проходит вне диэлектрика, так что надо положить ε=1, а q=(τ1+τ2)h, тогда
 , ,
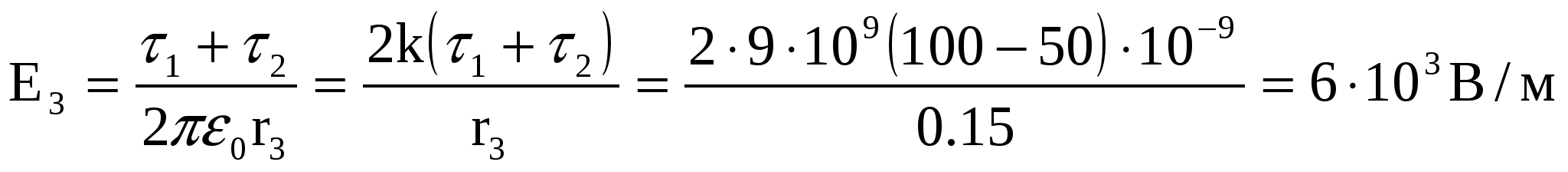
|
Ответ: E1=0
E2=104 В/м
E3=6.103 В/м
|
Пример 4.
На двух коаксиальных бесконечных цилиндрах радиусами 5 см и 10 см равномерно распределены заряды с линейными плотностями заряда τ1=100 нКл/м и τ2=50 нКл/м соответственно. Пространство между цилиндрами заполнено парафином с диэлектрической проницаемостью 2. Найти разность потенциалов цилиндров.
Дано:
τ1=100 нКл/м
τ2=50 нКл/м
R1=0.05 м
R2=0.1 м
ε=2
|
Решение:
Воспользуемся результатами, полученными в задаче 3: напряженность электростатического поля между цилиндрами, при R12, вычисленная по теореме Гаусса, равна:
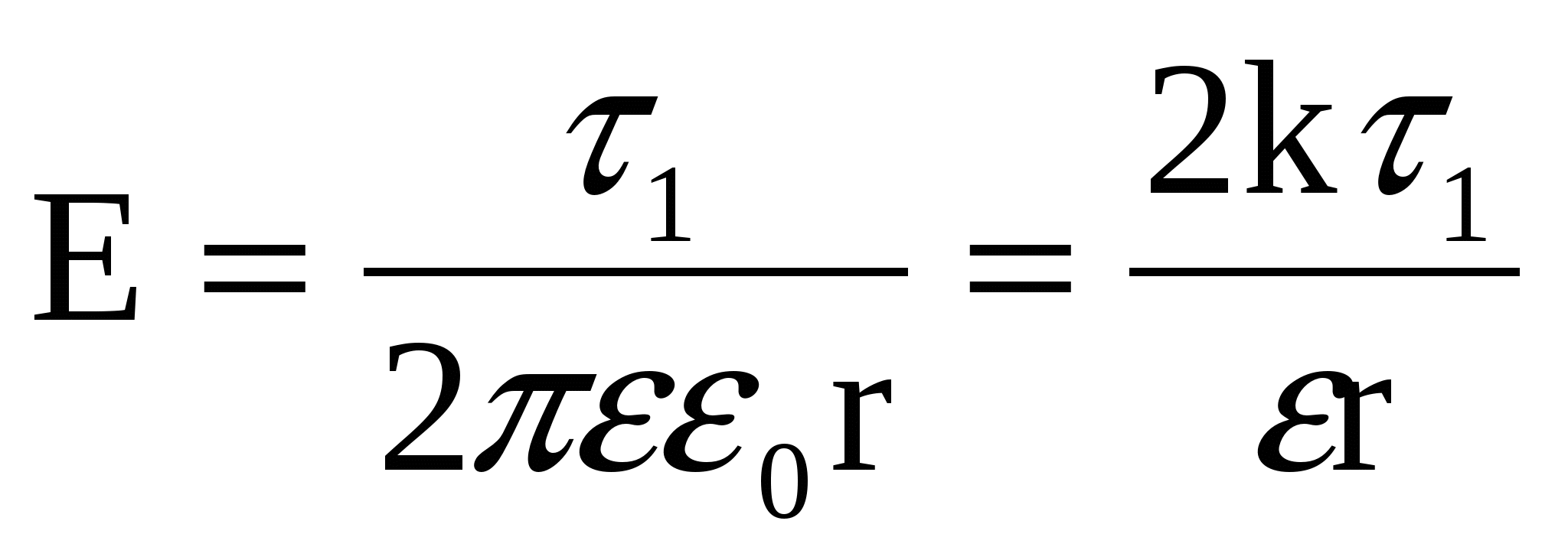 . (1) . (1)
По формуле связи между напряженностью и потенциалом
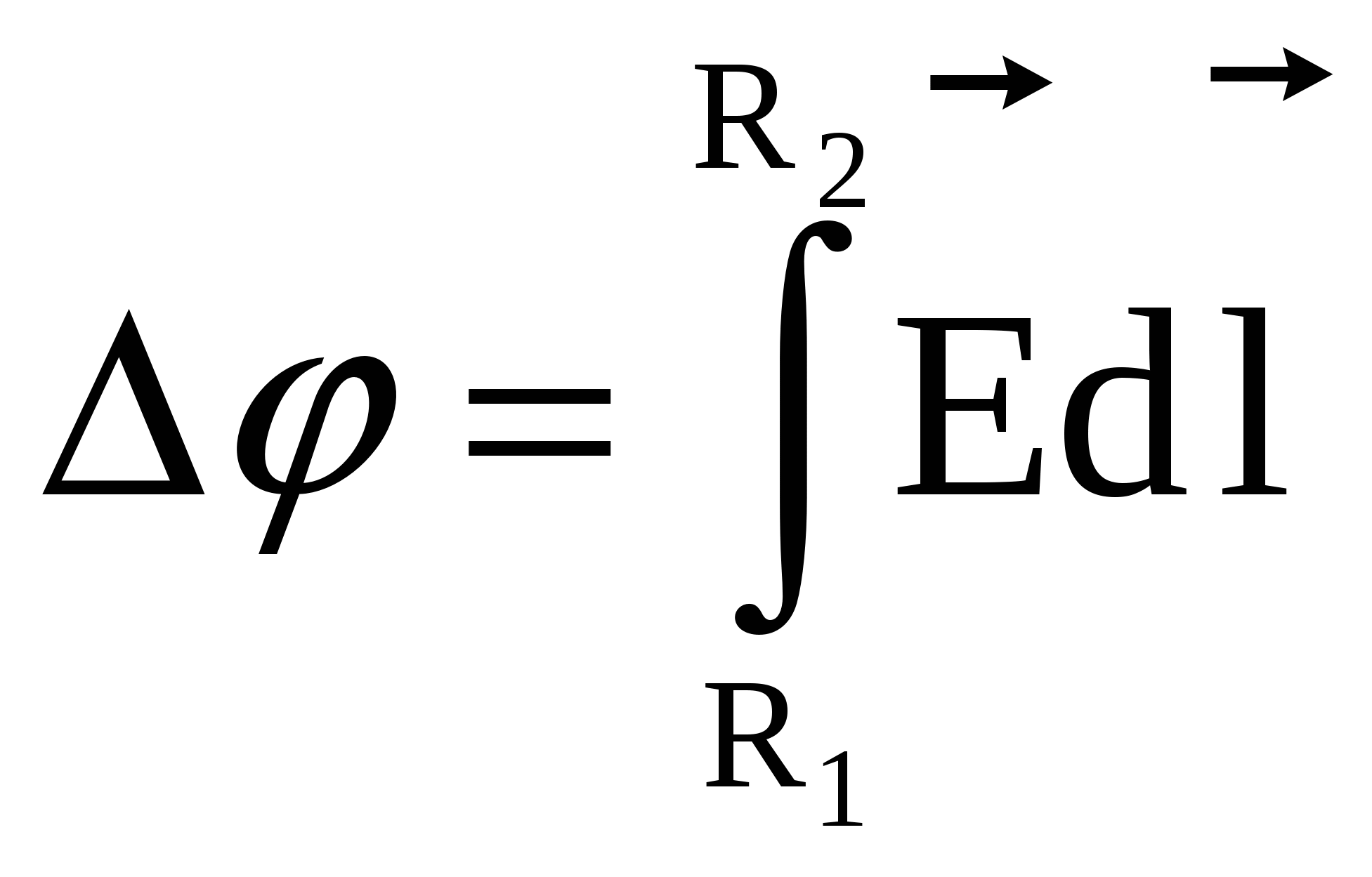 , (2) , (2)
где интеграл удобнее брать по силовой линии поля, так что 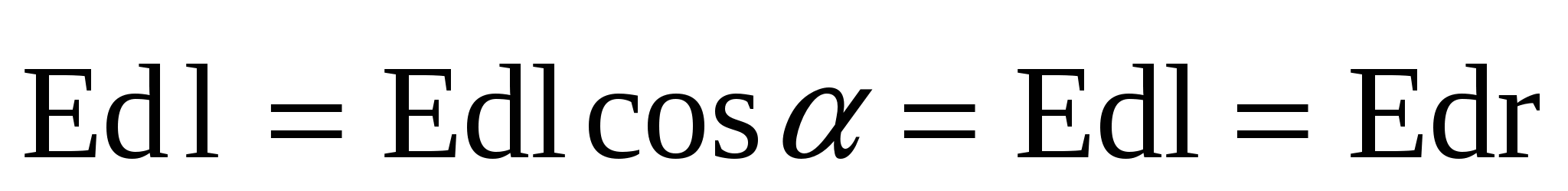 , так как направление напряженности , так как направление напряженности 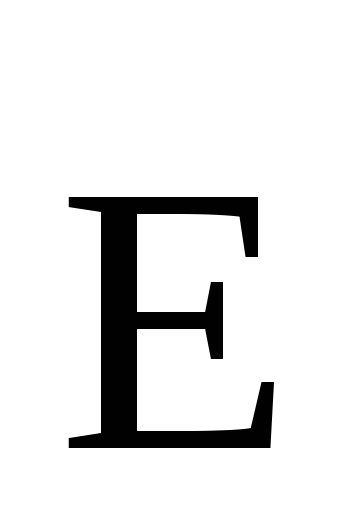 совпадает с направлением радиус-вектора совпадает с направлением радиус-вектора 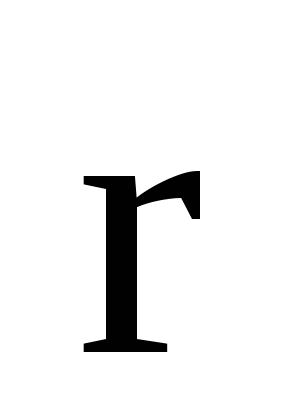 и элемента длины контура интегрирования и элемента длины контура интегрирования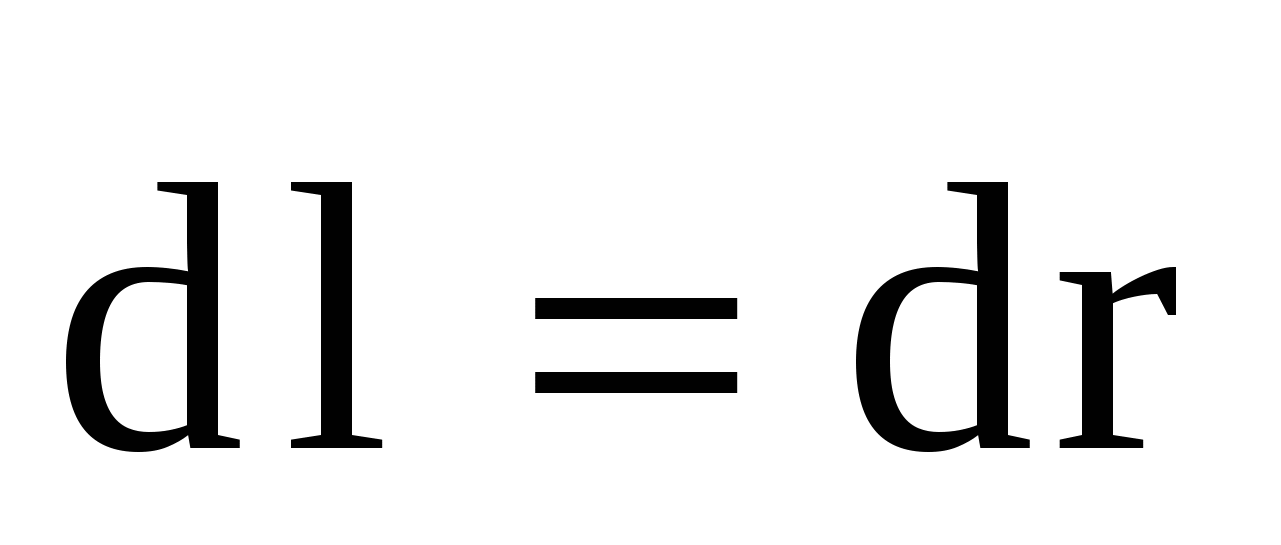 , α=0. Подставив (1) в (2), получим: , α=0. Подставив (1) в (2), получим:
 , ,
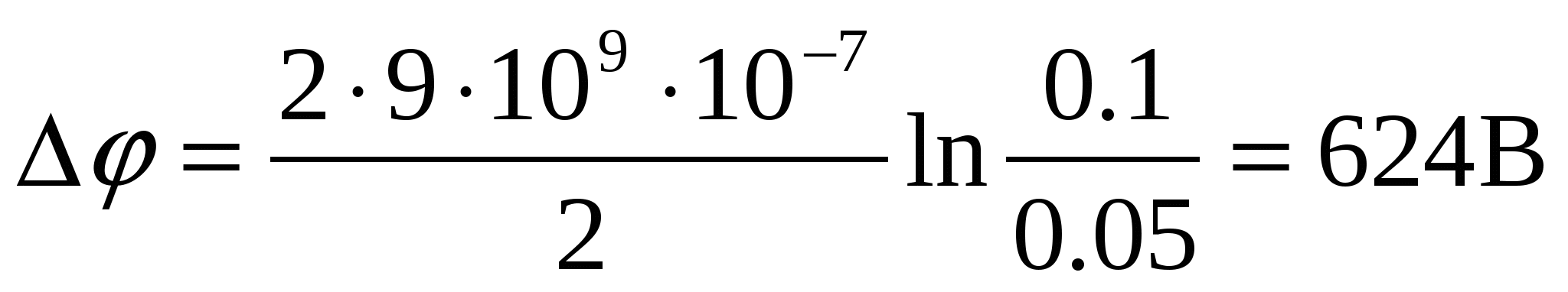
|
Найти:
Δφ=?
|
Ответ: Δφ=624 В
|
Пример 5.
Электрическое поле создано заряженной (Q=0.2 мкКл) металлической сферой радиусом 5 см. Какова энергия поля, заключенного в сферическом слое, ограниченном сферой и концентрической с ней сферической поверхностью, радиус которой в 3 раза больше радиуса сферы?
Дано:
Q=2.10-7 Кл
R0=0.05 м
R=0.15 м
|
Решение:
Энергию поля, заключенную в сферическом слое, будем находить через объемную плотность энергии, равную по определению
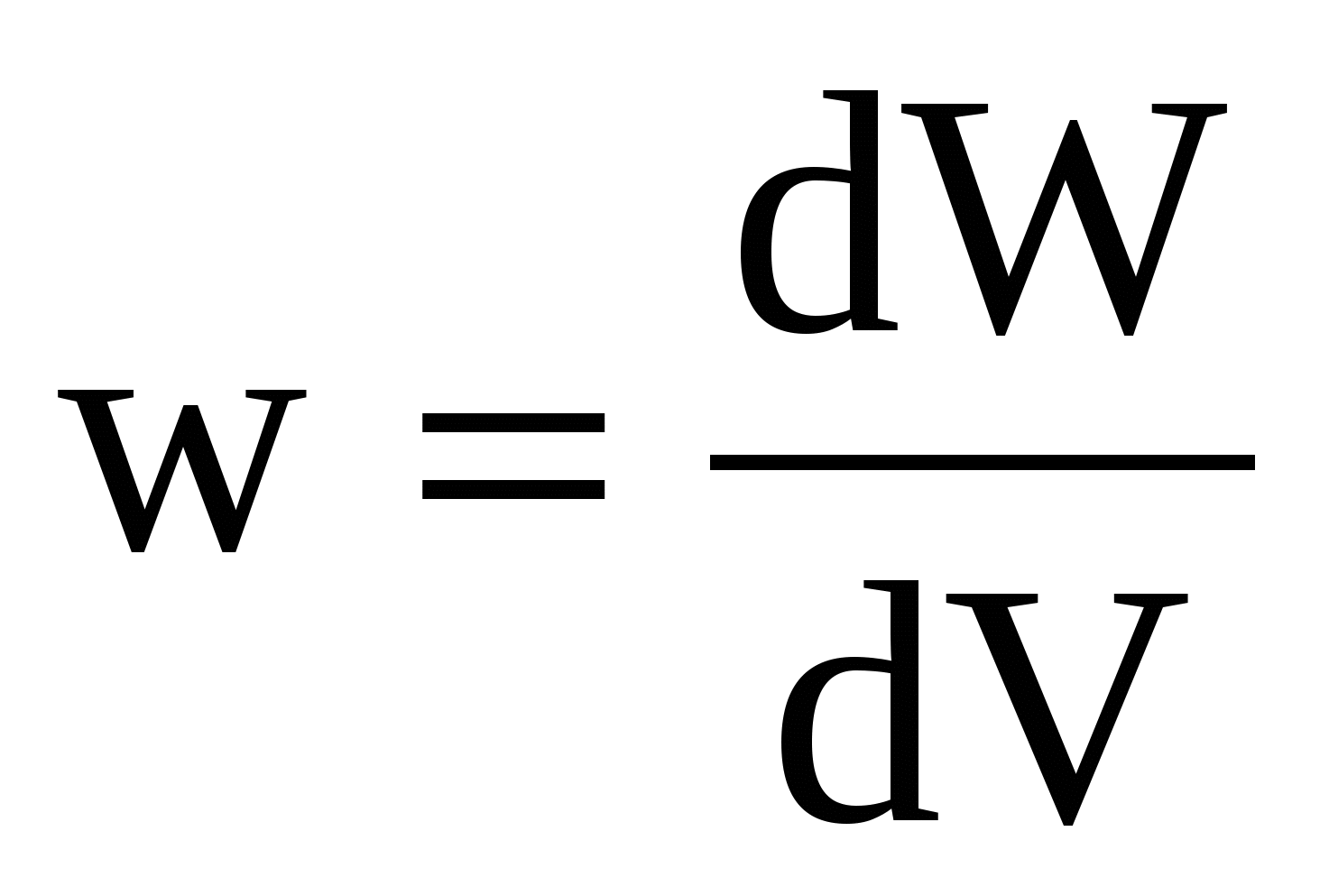 , (1) , (1)
а для энергии электростатического поля
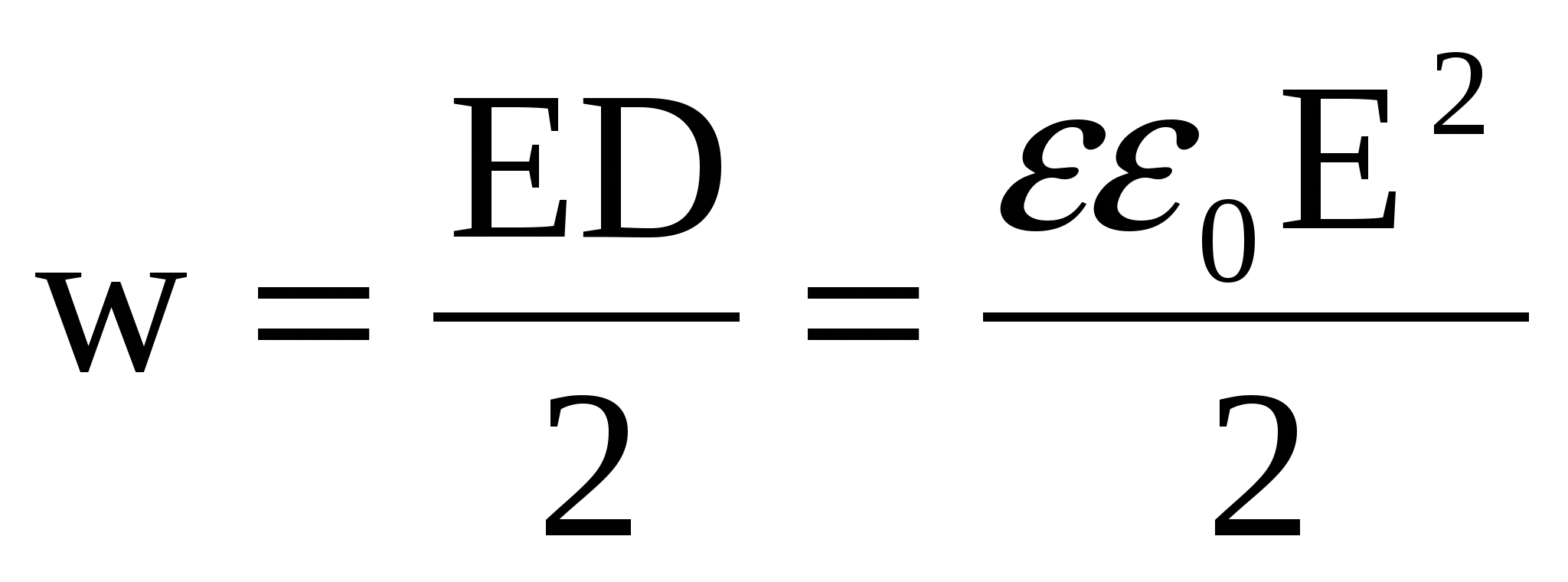 . (2) . (2)
Напряженность электростатического поля, созданного уединенной металлической заряженной сферой, вне этой сферы (при r>R0) такая же, как и напряженность поля точечного заряда, находящегося в центре сферы:
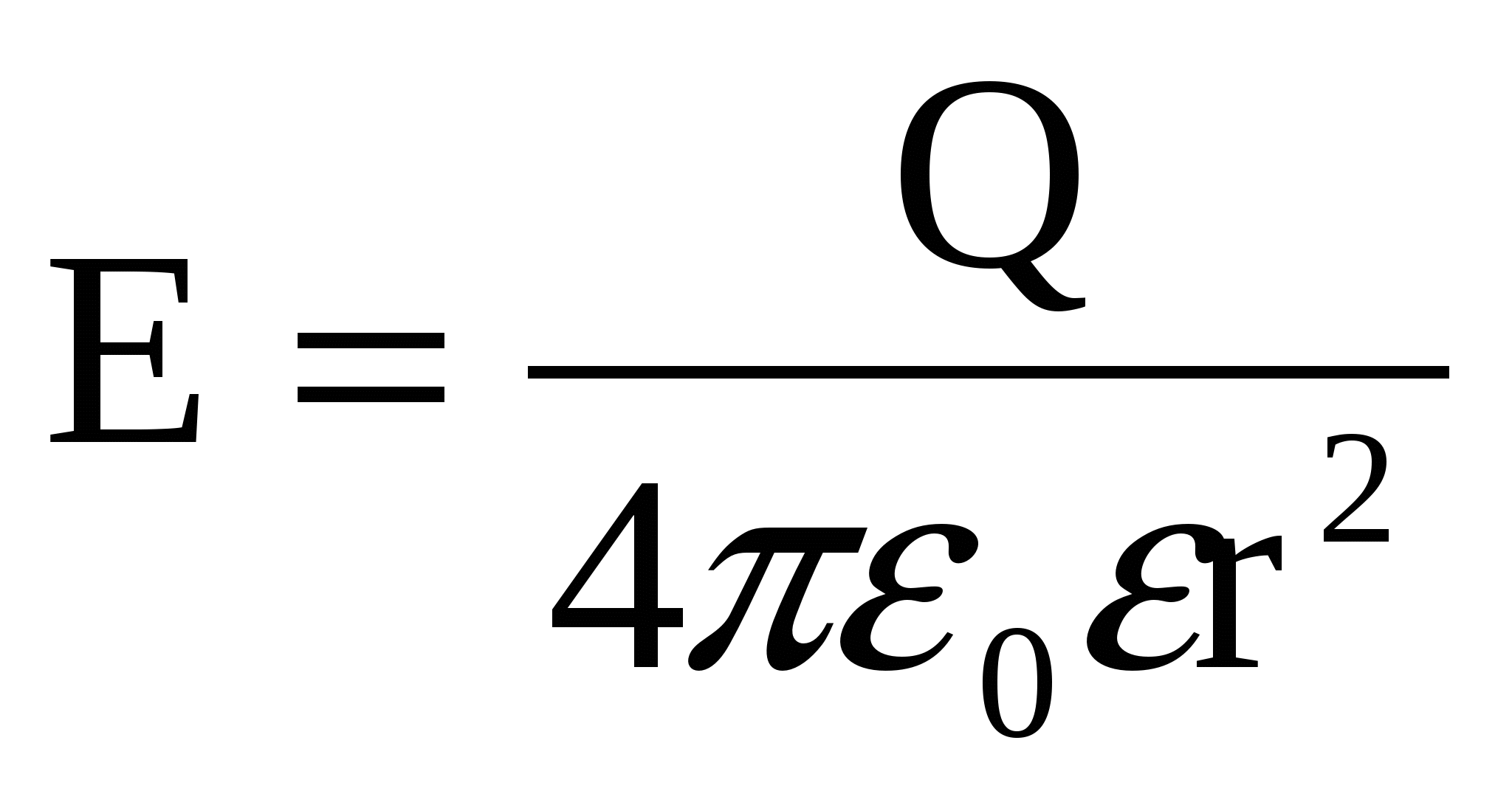 , (3) , (3)
причем будем считать, что ε=1 (поле в вакууме).
Из (1) – (3) следует, что энергия, заключенная в любом малом объеме dV, равна:
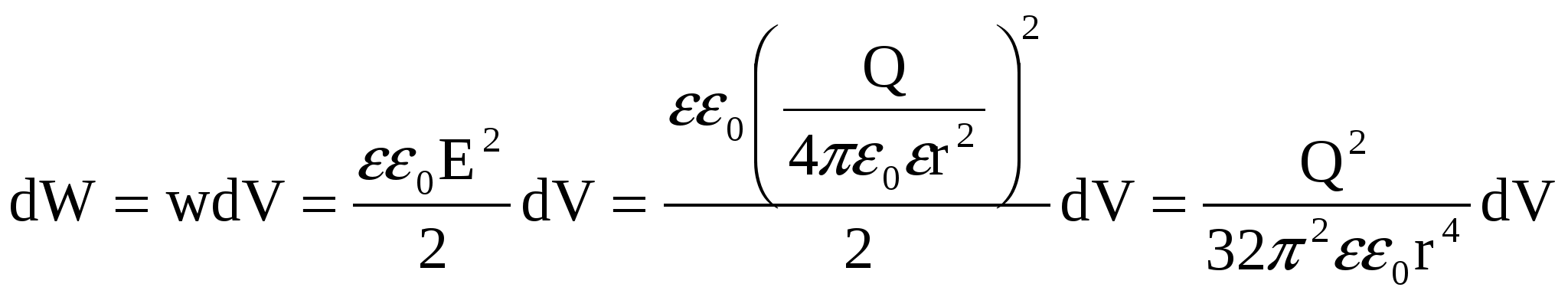 . (4) . (4)
Поскольку поле сферически симметрично, в качестве dV следует брать тонкий шаровой слой, концентрический данной сфере, с внутренним радиусом r, внешним радиусом (r+dr), тогда в пределах этого слоя значение напряженности можно считать одинаковым и равным (3). Объем слоя можно найти, перемножив площадь сферы на его толщину, так как слой тонкий:
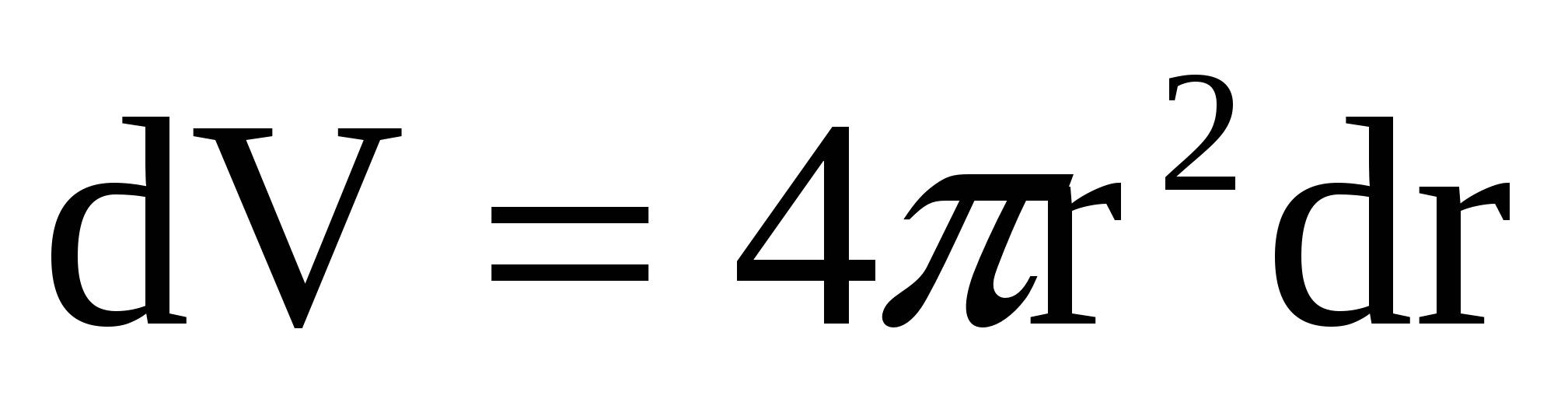 . (5) . (5)
Наконец, искомую энергию находим, проинтегрировав (4) по объему, то есть в пределах R0
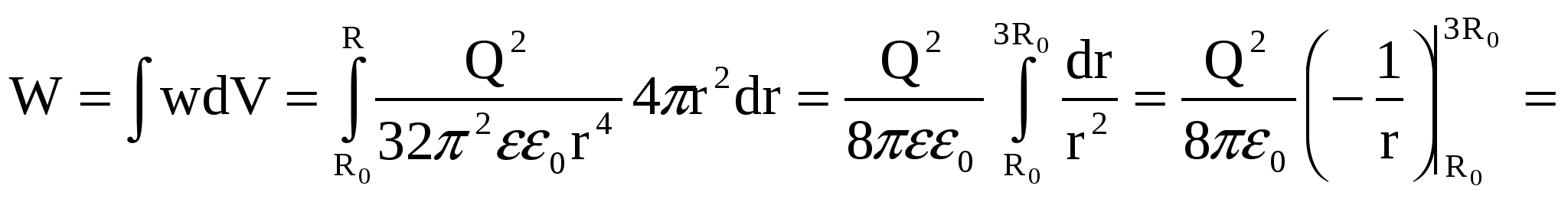
|
Найти:
W=?
|
|
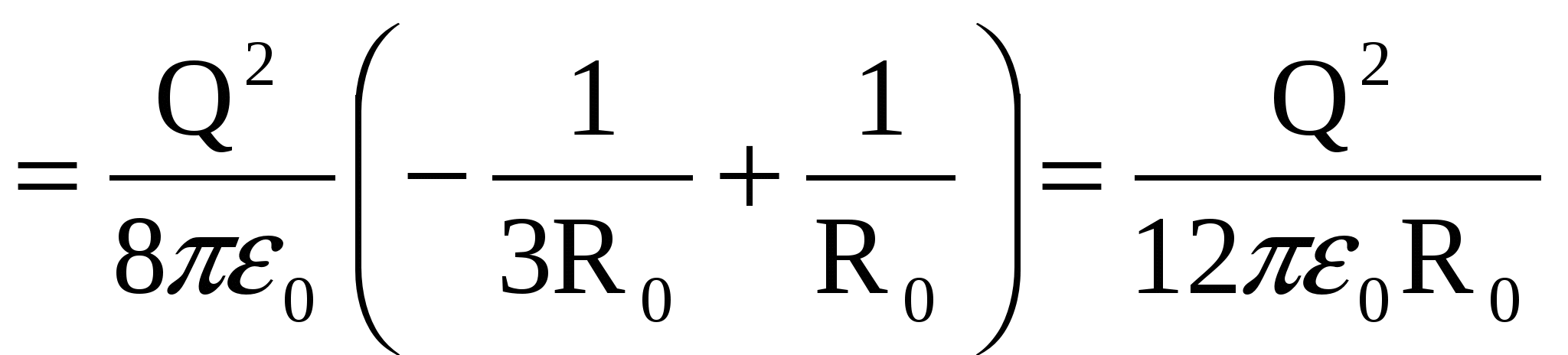 , ,
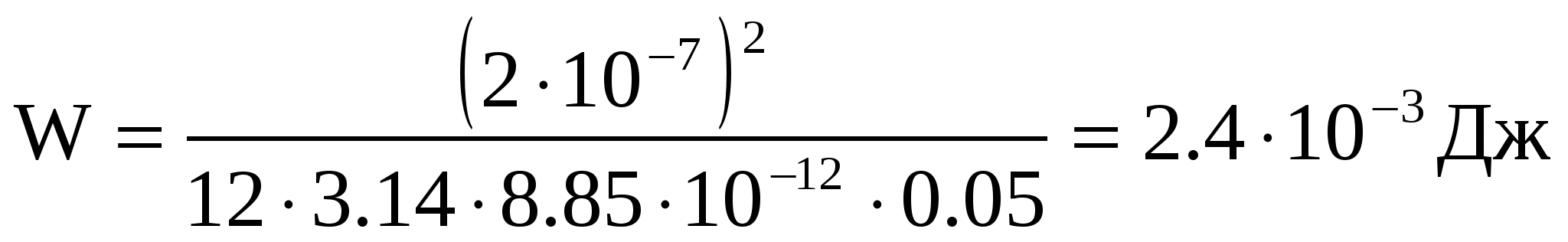
|
Ответ: W=2.4 мДж
|
Пример 6.
Напряженность поля воздушного конденсатора, заряженного и отключенного от источника, равна E0. В конденсатор параллельно обкладкам поместили пластину диэлектрика с диэлектрической проницаемостью ε. Найти поверхностную плотность связанных зарядов на гранях диэлектрика, выразить ее через поверхностную плотность свободных зарядов на обкладках конденсатора; найти напряженность поля в диэлектрике, а также напряженность поля, созданного только связанными зарядами; значение вектора электрического смещения и поляризованности диэлектрика.
Дано:
E0
ε
|
Решение:
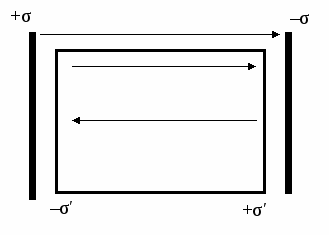
Напряженность поля в диэлектрике уменьшается по сравнению с напряженностью в вакууме в ε раз, поэтому
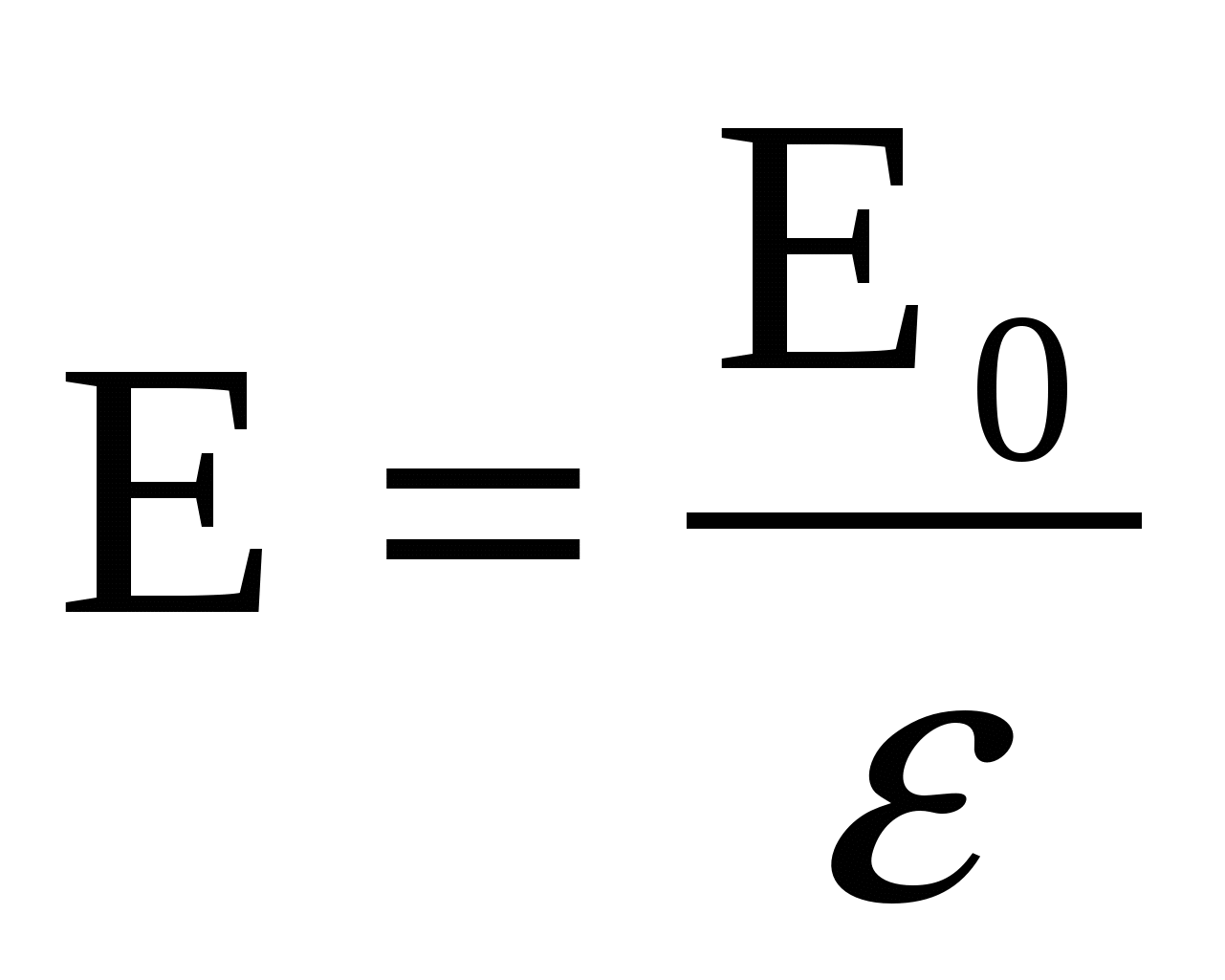 . (1) . (1)
Суммарное (полное) поле в диэлектрике складывается из поля свободных зарядов 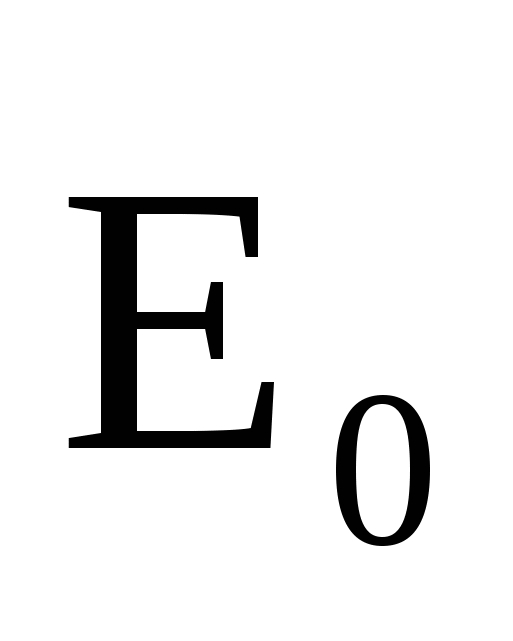 и связанных (индуцированных) и связанных (индуцированных) 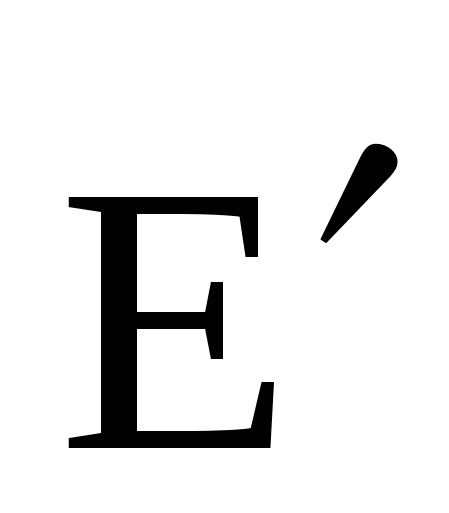 : : 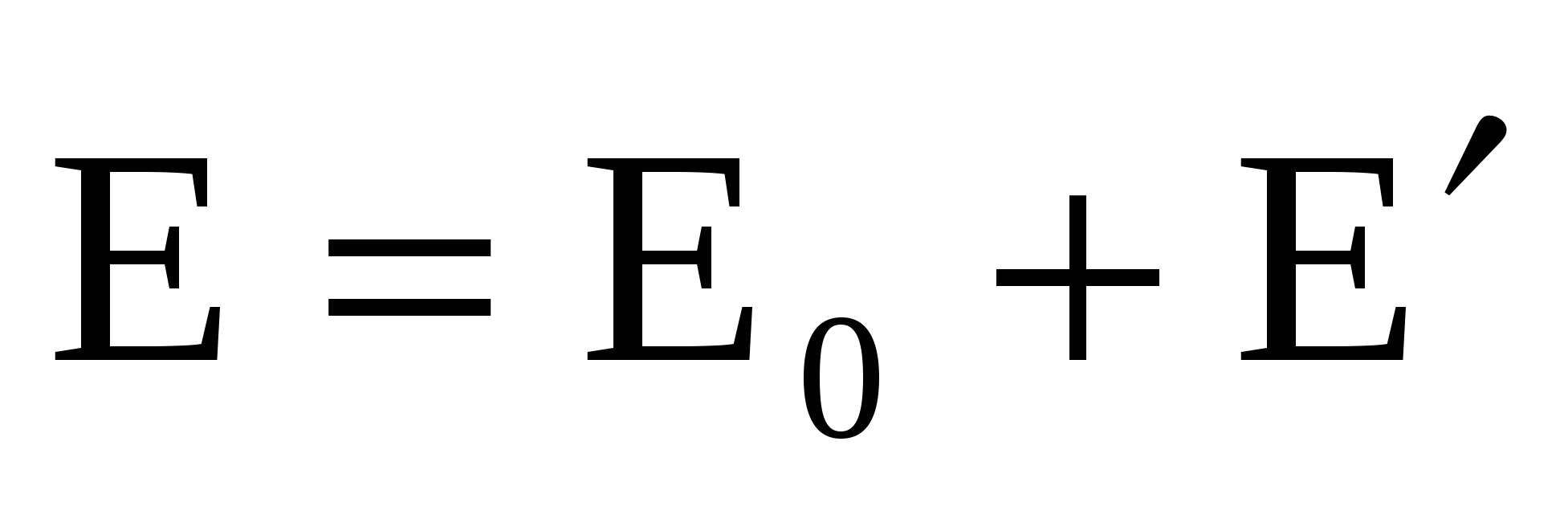 , но , но 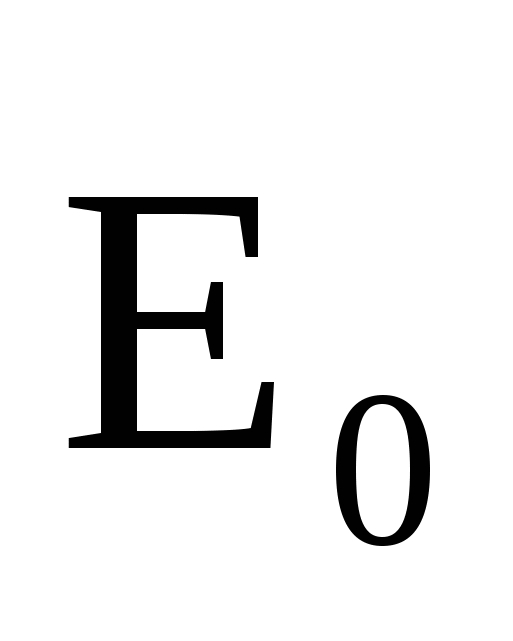 и и 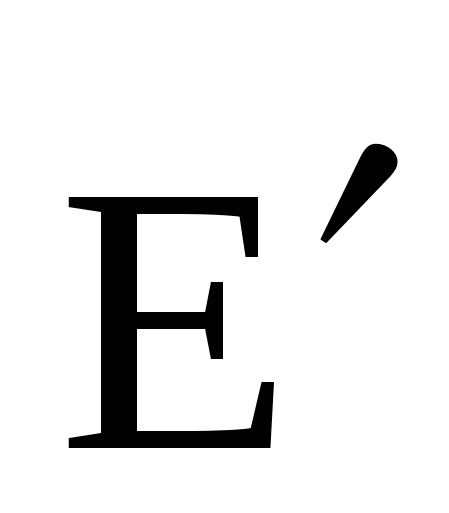 направлены противоположно (см. рис.), поэтому E=E0–E′, направлены противоположно (см. рис.), поэтому E=E0–E′,
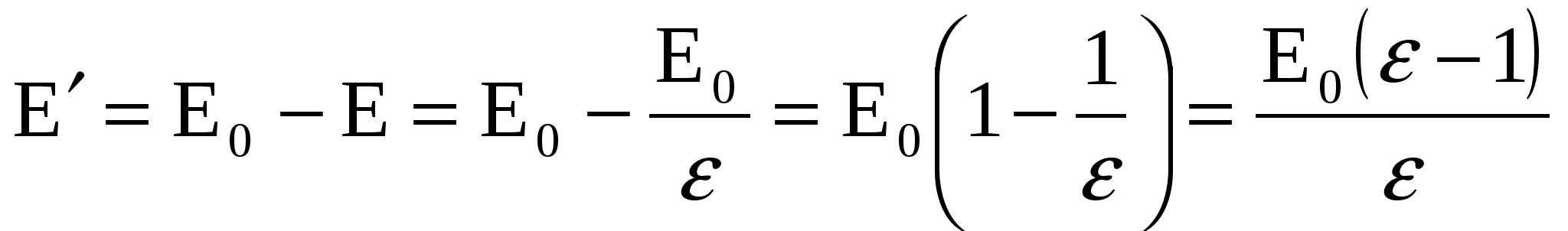 . (2) . (2)
Напряженность поля связанных зарядов можно выразить через поверхностную плотность связанных зарядов (напряженность поля конденсатора):
|
Найти:
σ′=?
Е=?
E′=?
D=?
P=?
|
|
 , (3) , (3)
тогда с учетом (2):
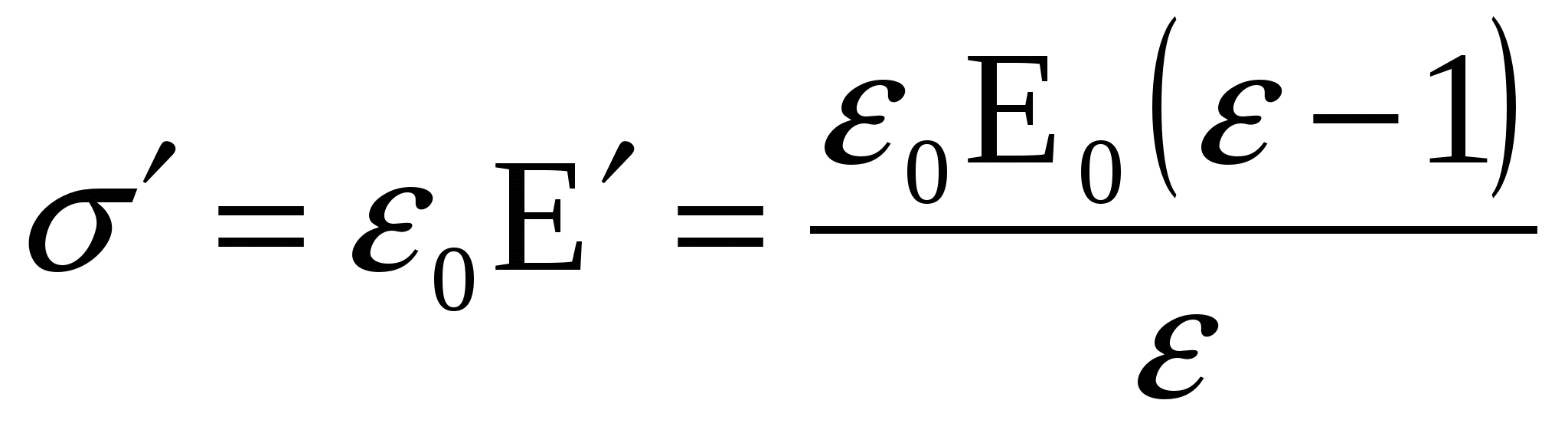 . (4) . (4)
Аналогично, напряженность поля только свободных зарядов 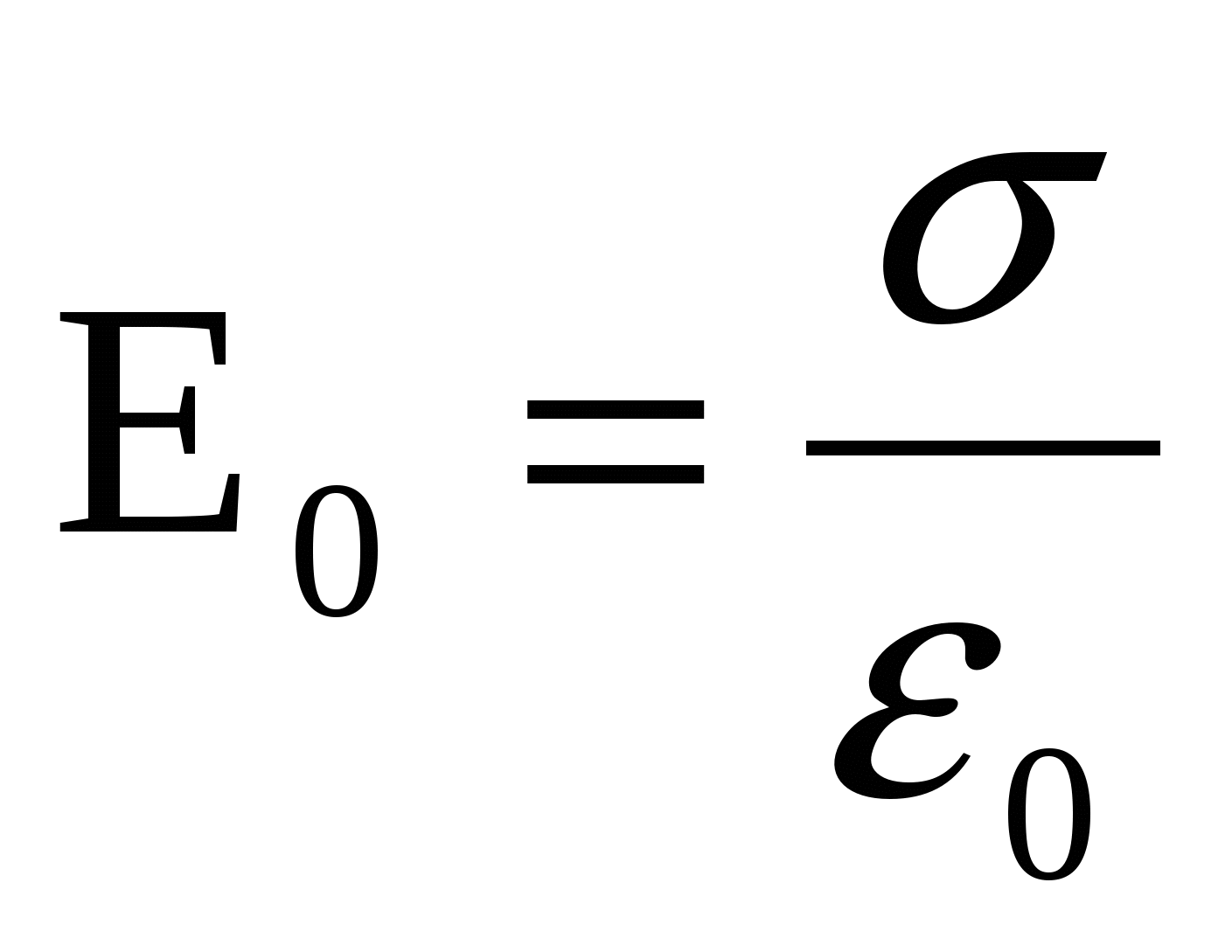 , тогда из (4): , тогда из (4):
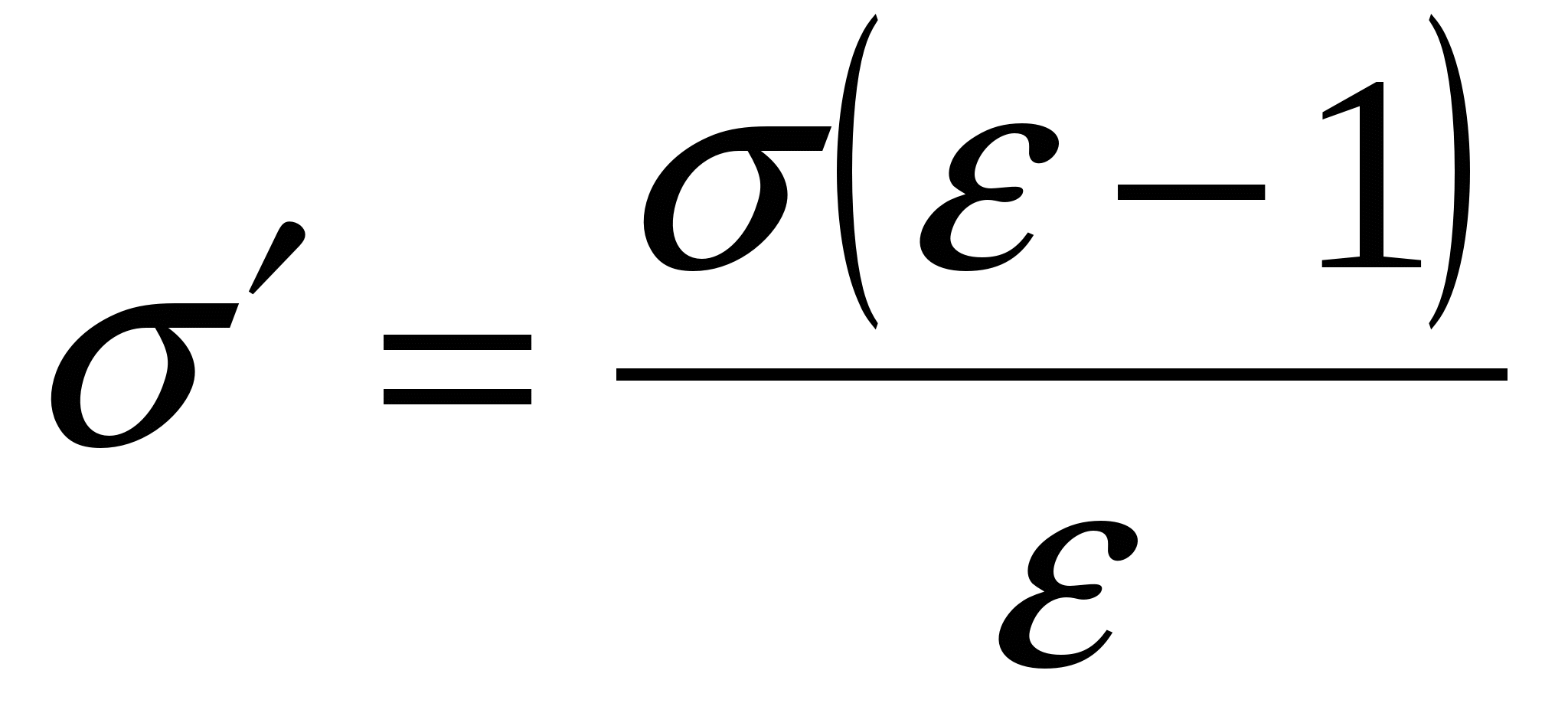 . (5) . (5)
Вектор электрического смещения 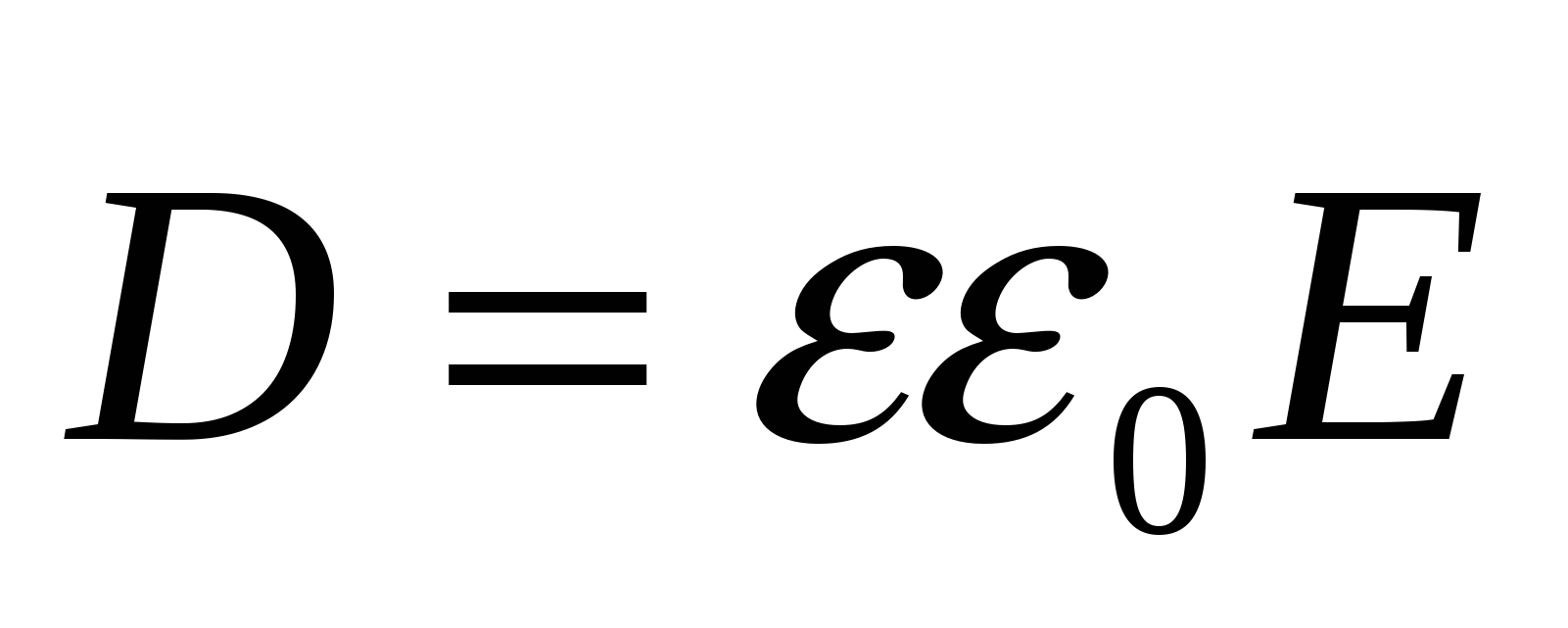 , поэтому , поэтому
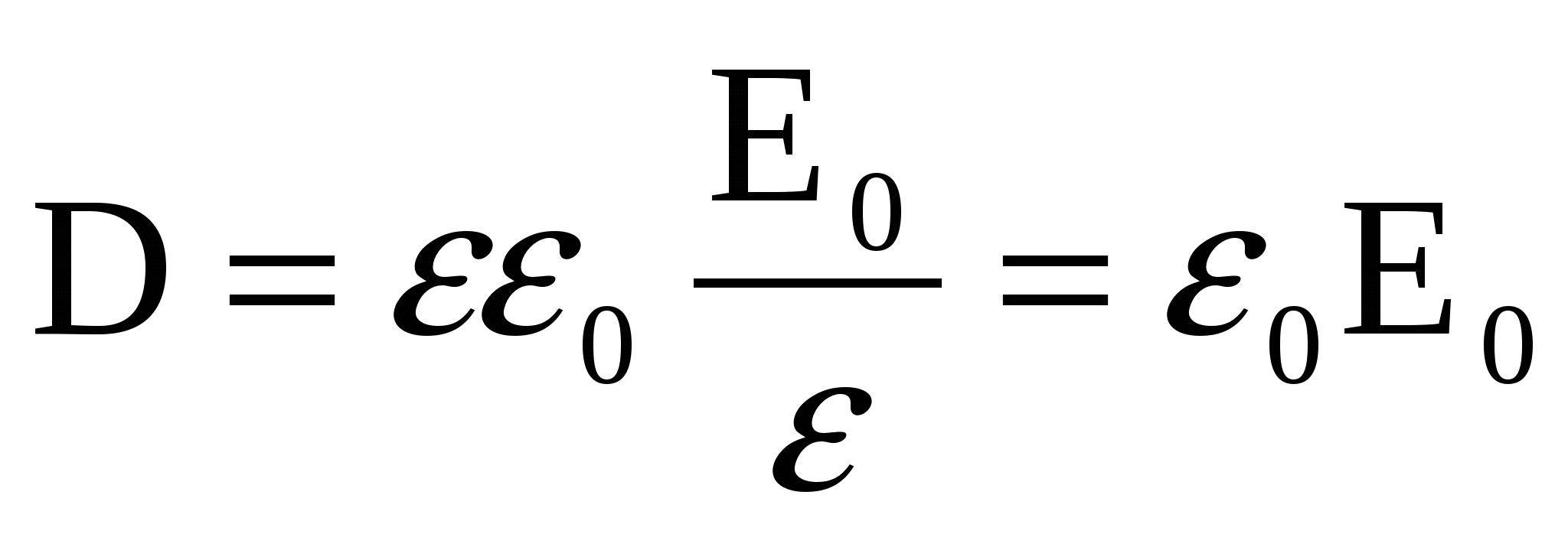 . (6) . (6)
Далее, так как 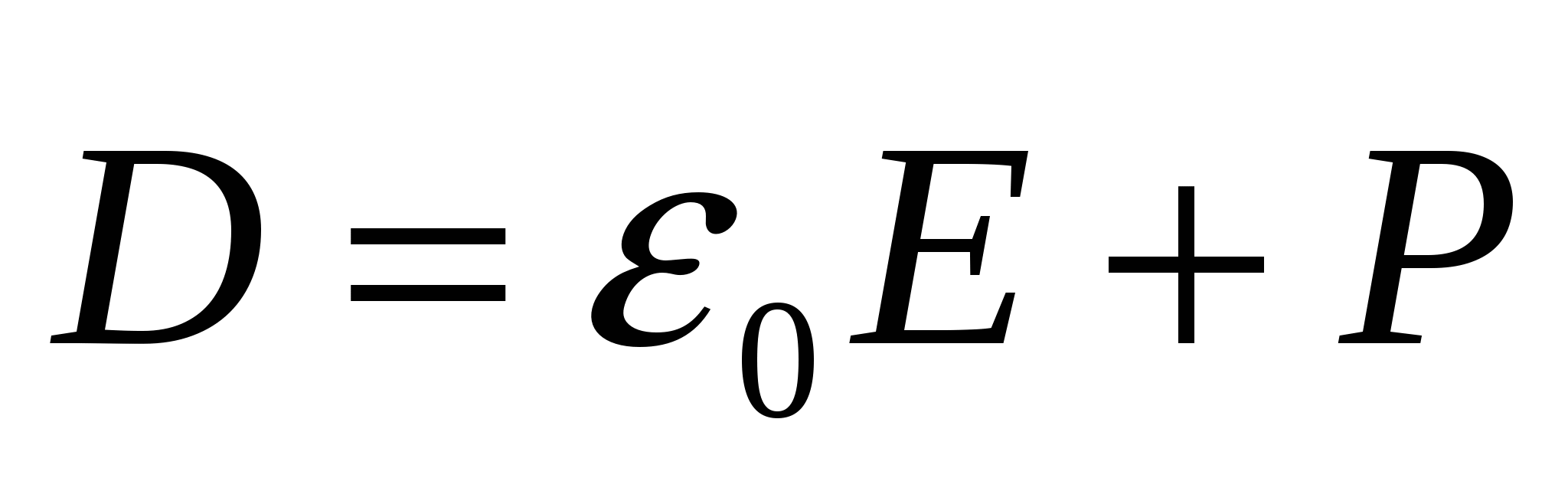 и векторы и векторы 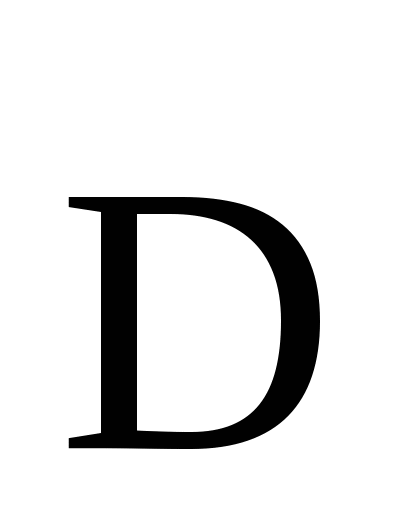 , , 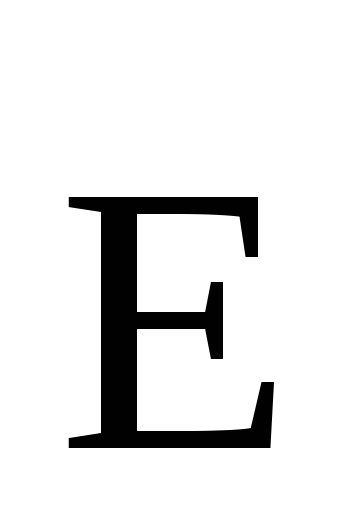 и и 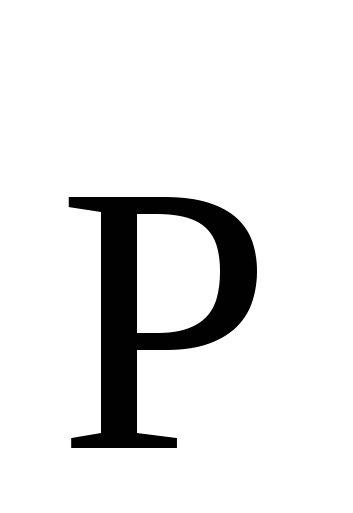 направлены одинаково, то: направлены одинаково, то:
 . (7) . (7)
Можно выполнить проверку (7): по определению вектор поляризации равен суммарному дипольному моменту единицы объема вещества:
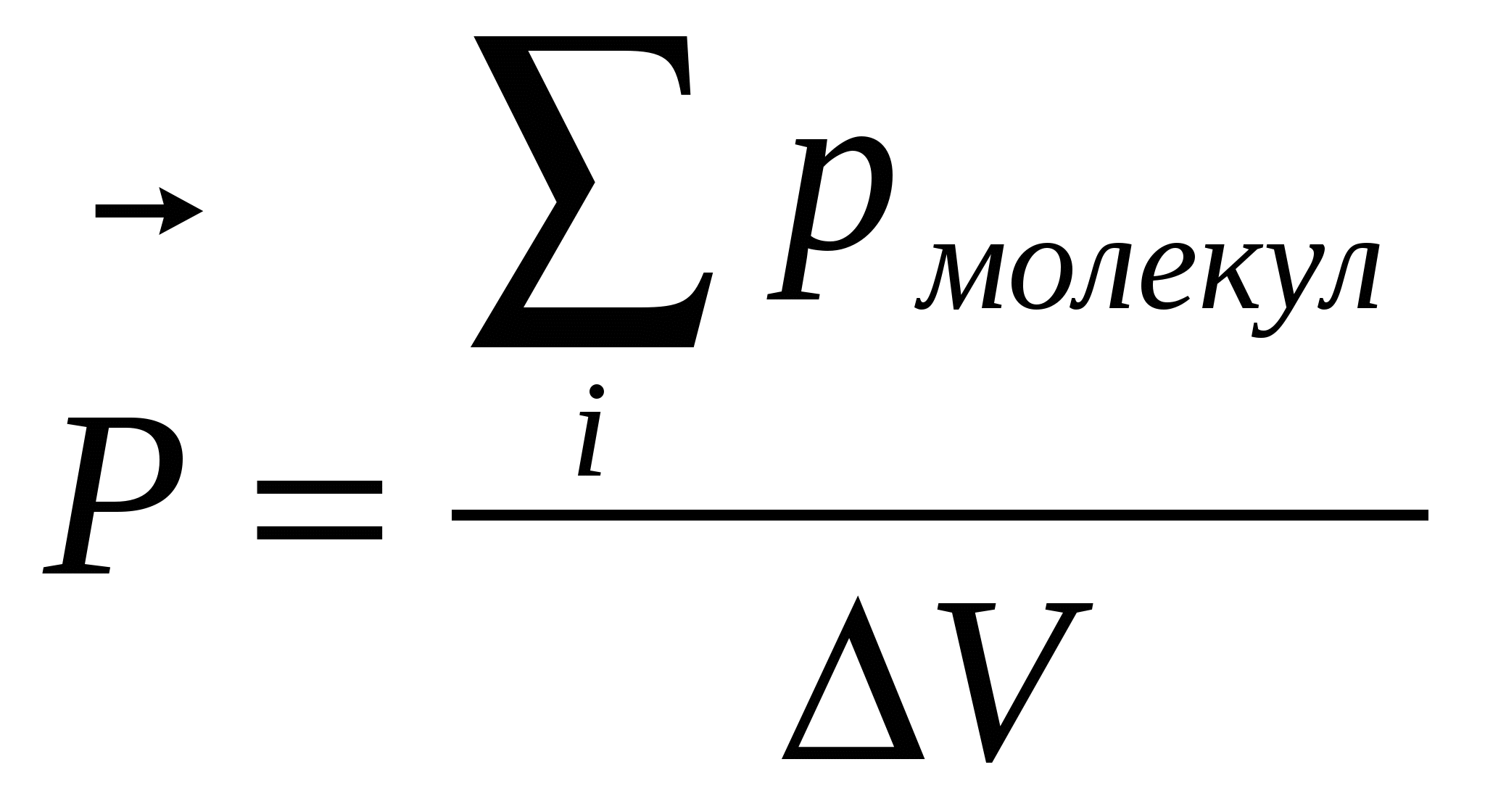 , (8) , (8)
а дипольный момент пластины диэлектрика равен произведению связанного заряда, локализованного на одной из граней 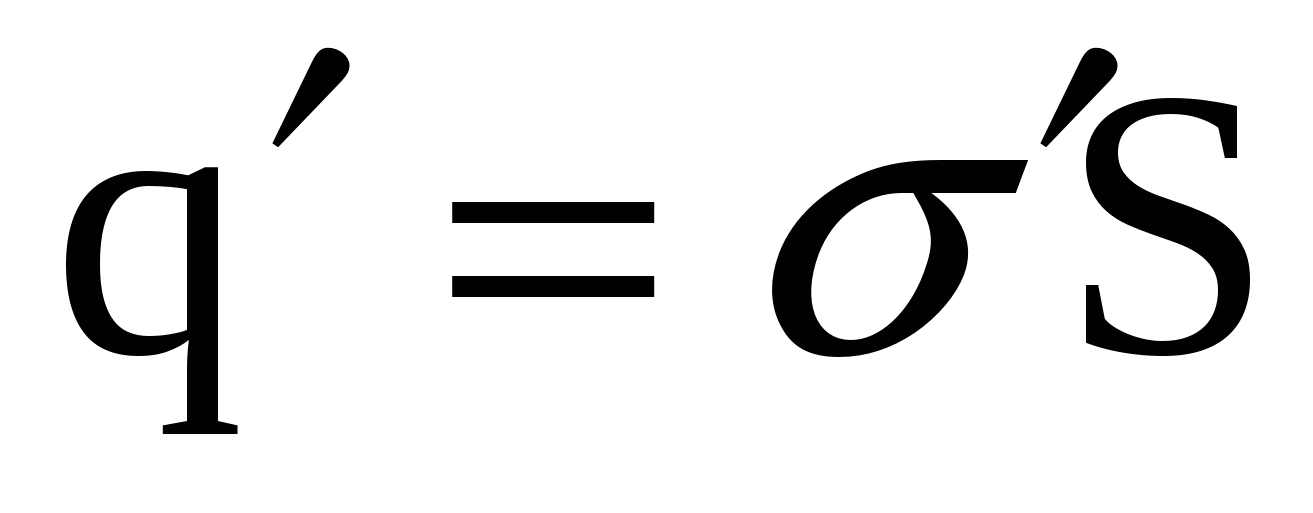 , на плечо диполя – толщину пластины d, тогда , на плечо диполя – толщину пластины d, тогда
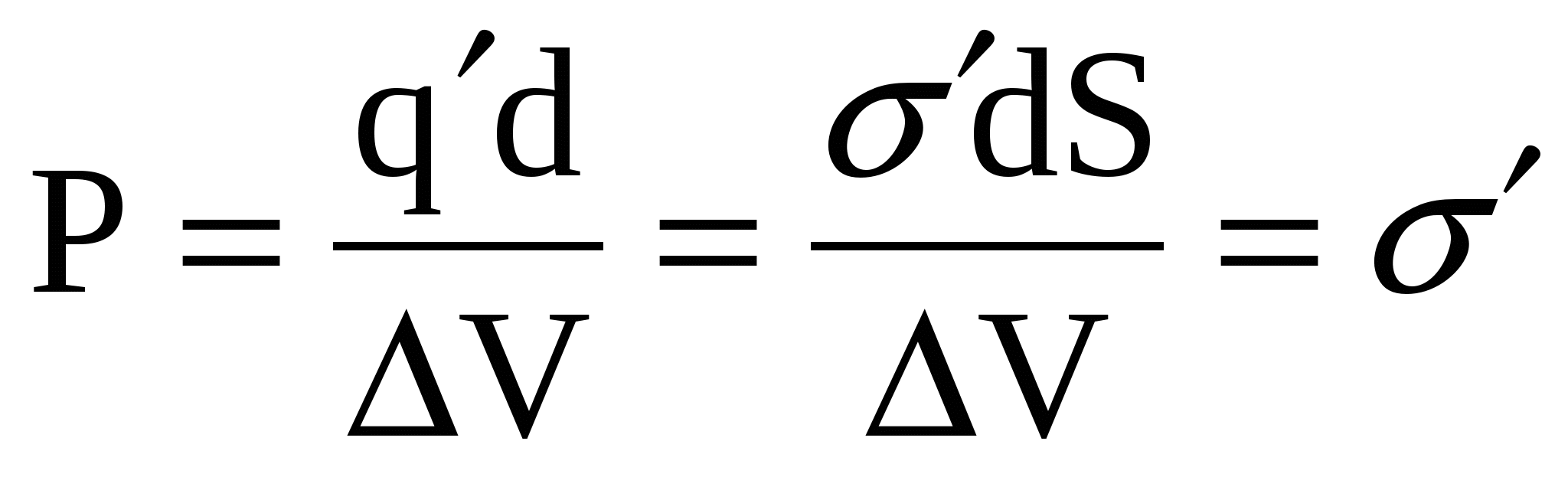 , (9) , (9)
так как объем пластины ΔV=Sd. Из (4) и (9) получаем (7).
|
Ответ: 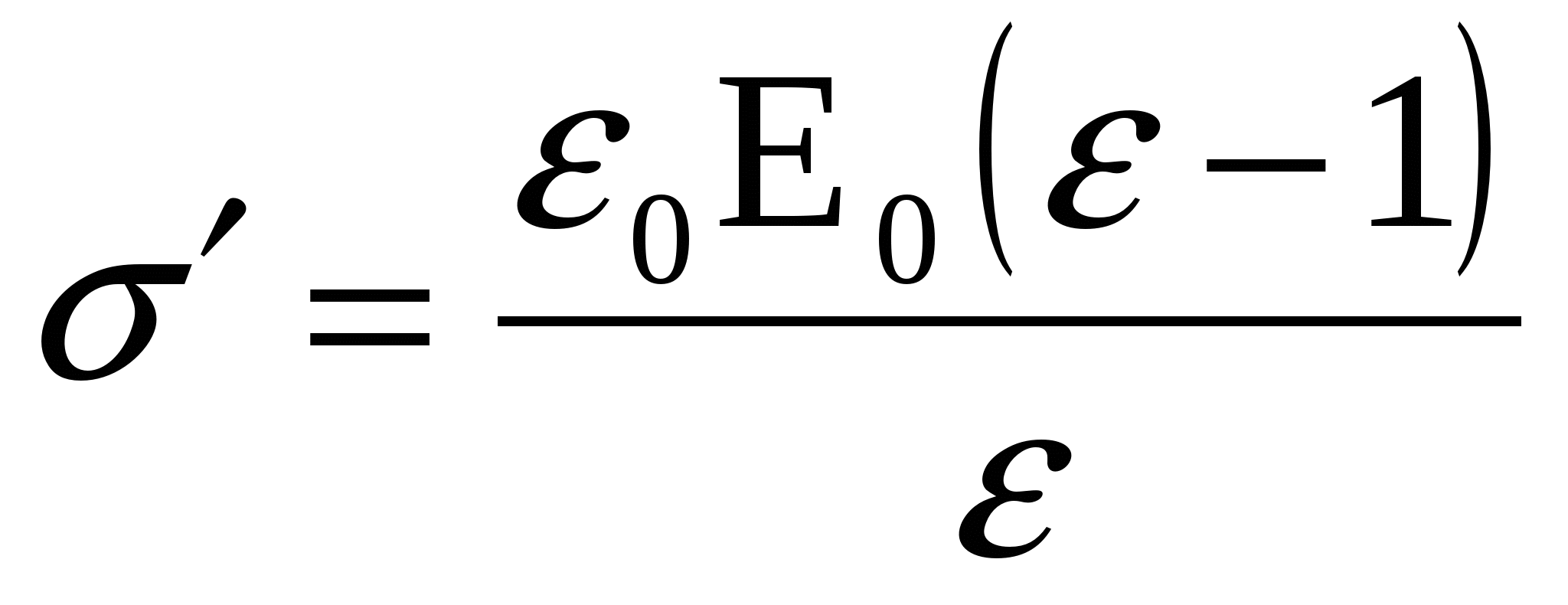
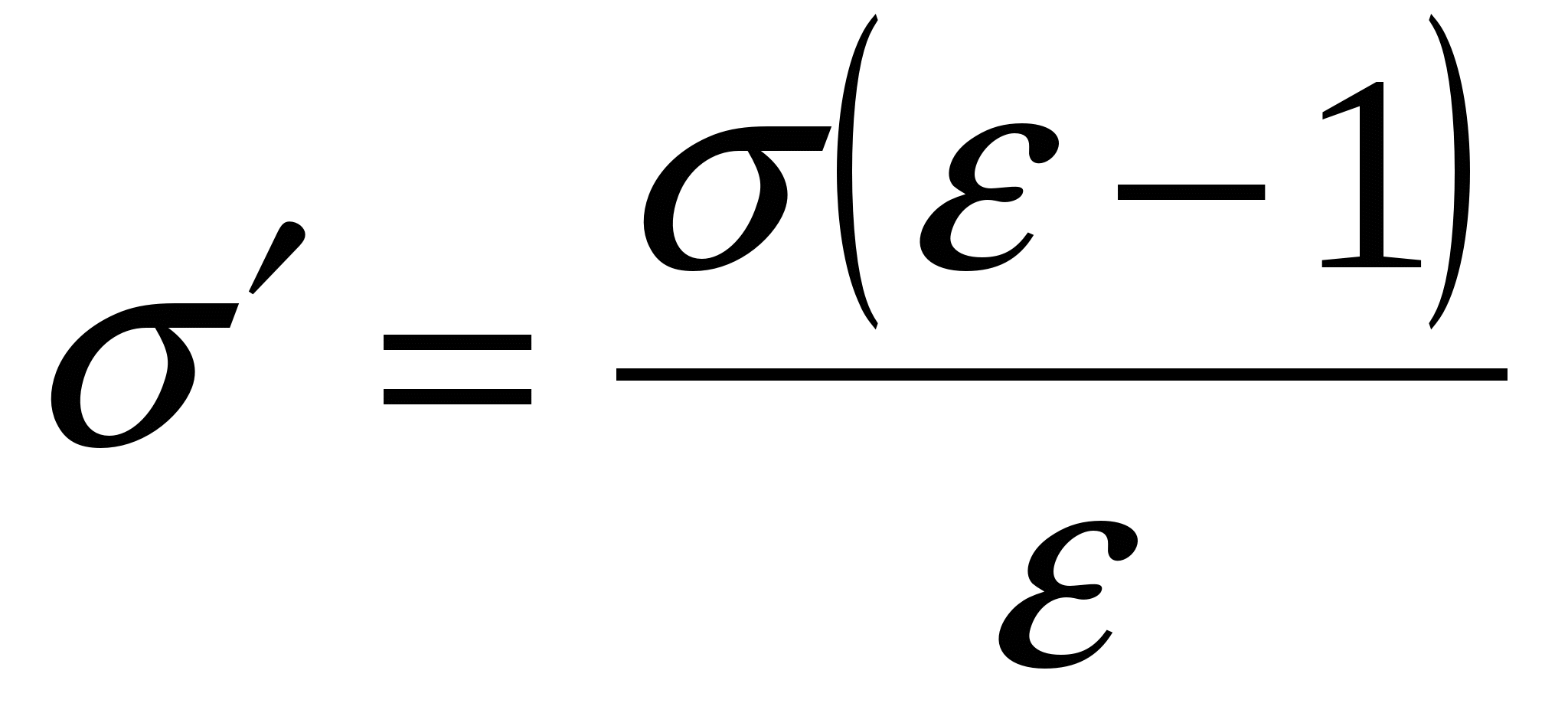
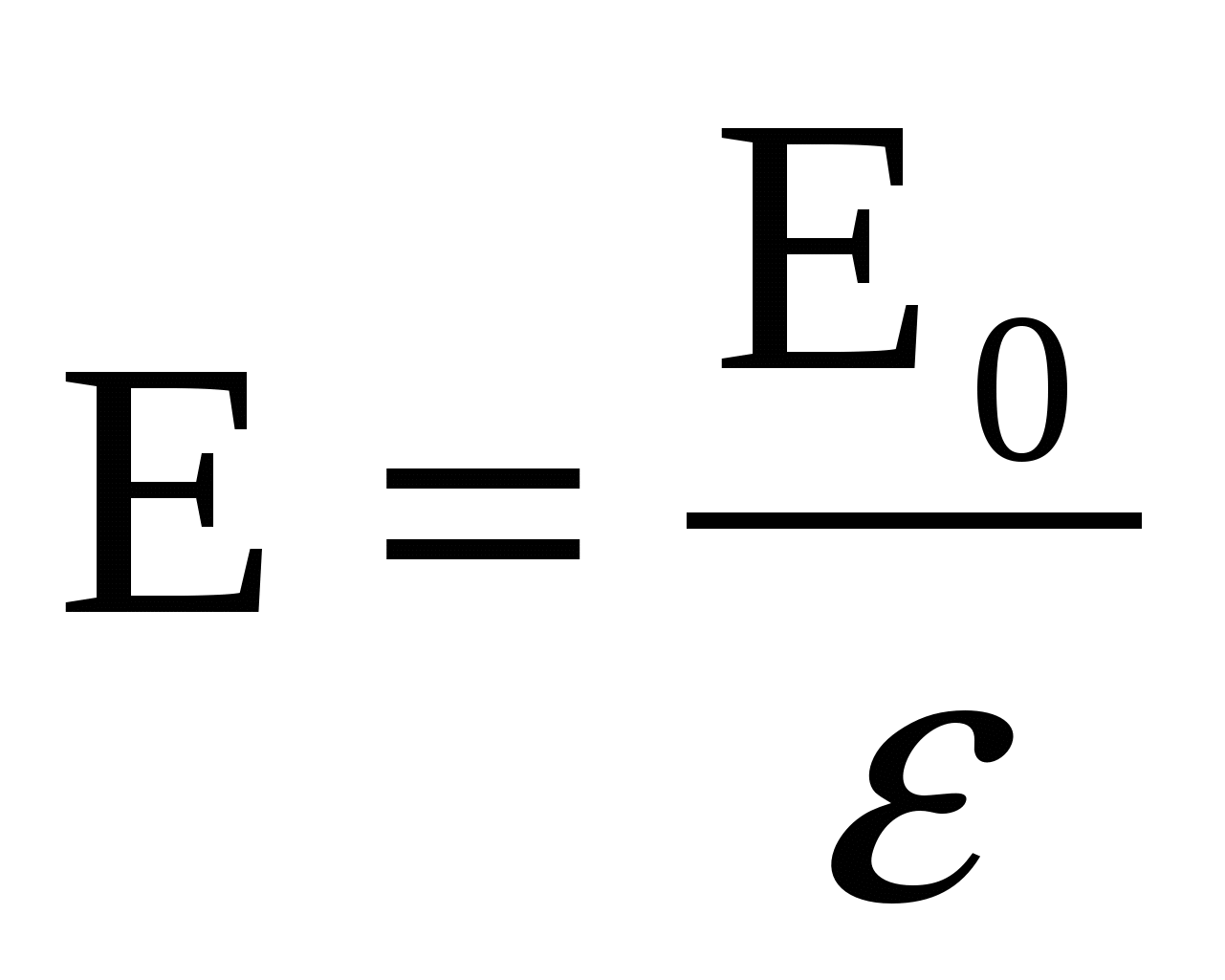
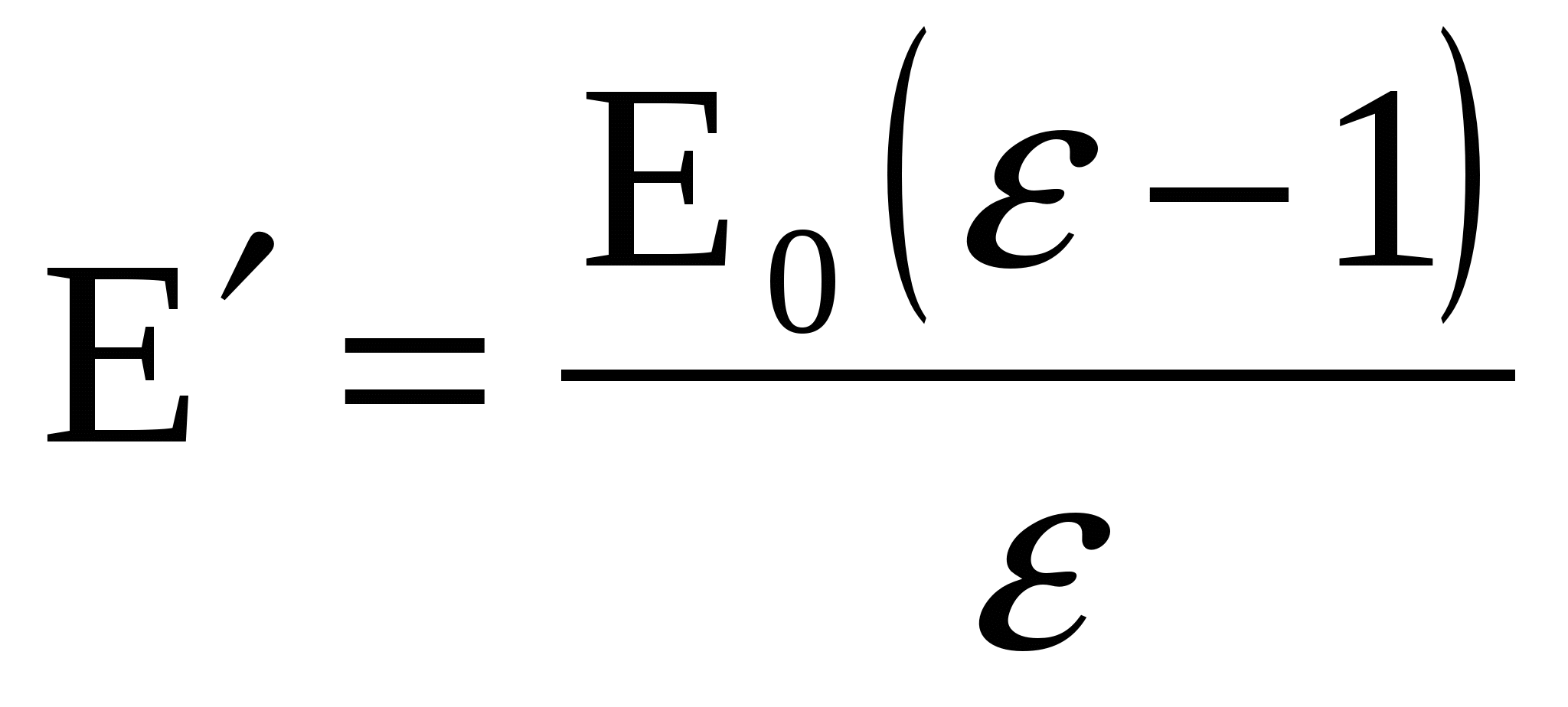
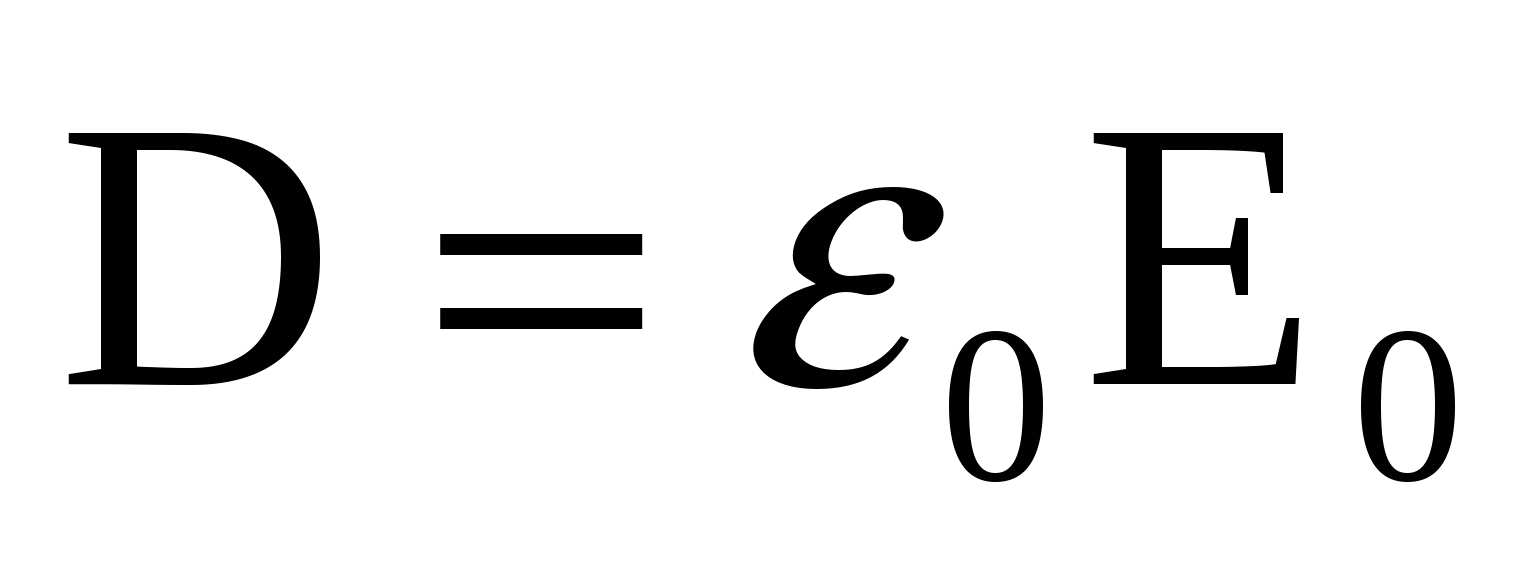

|
Пример 7.
О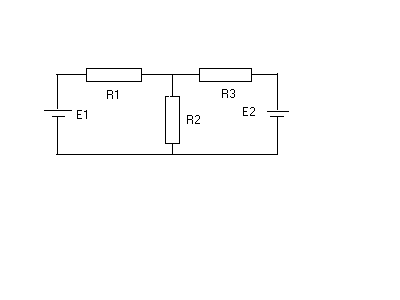 пределить силу тока в сопротивлении R3 и напряжение на концах этого сопротивления. Е1=1 В, Е2=5 В, R1=1 Ом, R2=2 Ом, R3=3 Ом. пределить силу тока в сопротивлении R3 и напряжение на концах этого сопротивления. Е1=1 В, Е2=5 В, R1=1 Ом, R2=2 Ом, R3=3 Ом.
Дано:
Е1=1 В
Е2=5 В
R1=1 Ом
R2=2 Ом
R3=3 Ом
|
Решение:
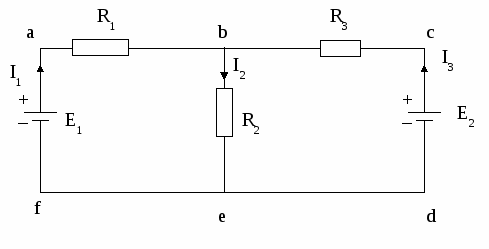

Для решения задачи используем правила Кирхгофа. В первую очередь выберем направления токов во всех ветвях цепи (в данной задаче их три) и проставим обозначения токов (см. рис.). В цепи 2 узла (b и e), следовательно, по первому правилу должно быть записано одно уравнение (на одно меньше, чем количество узлов): 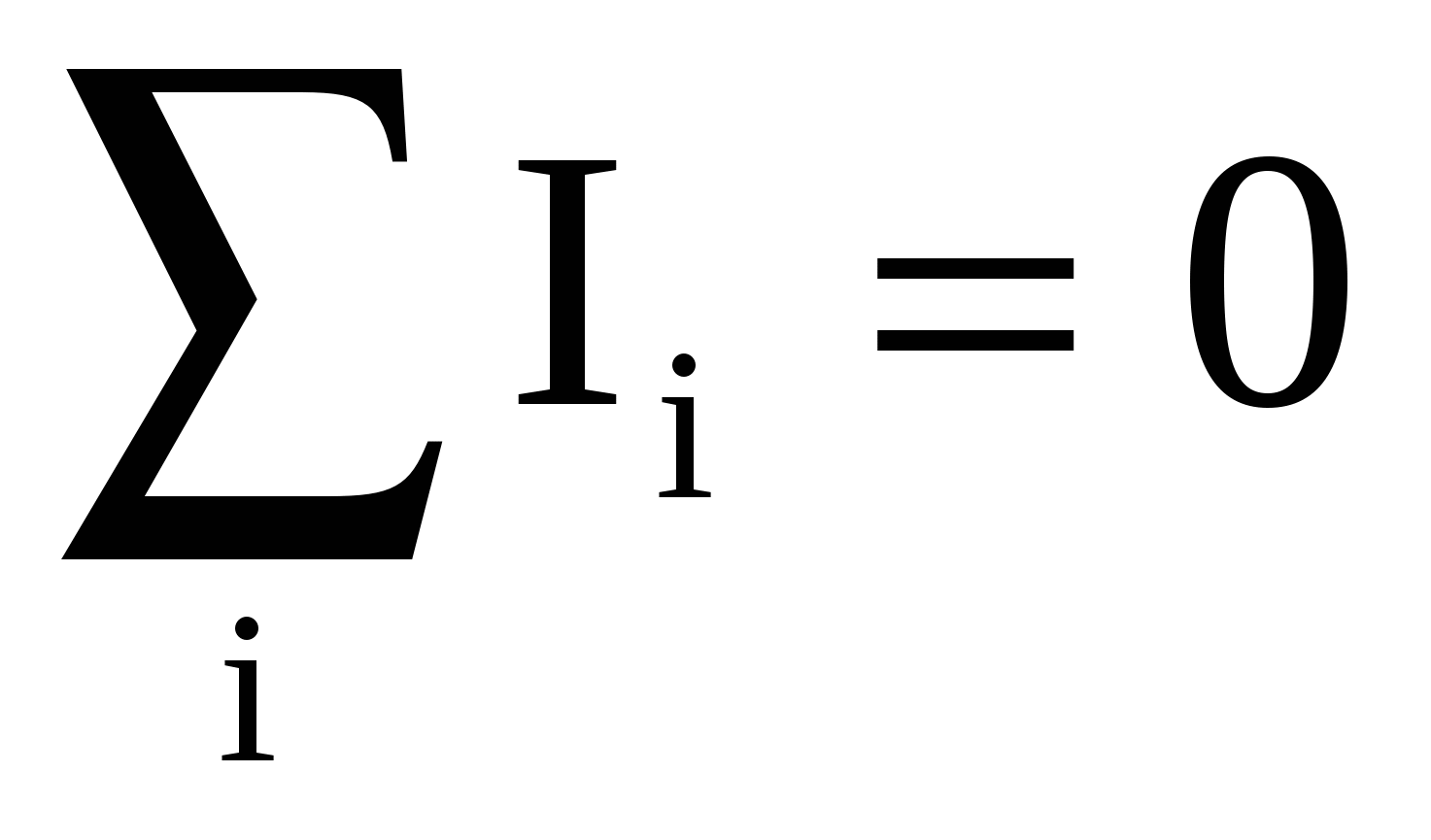 - алгебраическая сумма токов, сходящихся в узле, равна нулю. Запишем это правило для узла b: - алгебраическая сумма токов, сходящихся в узле, равна нулю. Запишем это правило для узла b:
I1–I2+I3=0, (1)
Причем токи, заходящие в узел, берем с положительным знаком, выходящие – с отрицательным.
По второму правилу Кирхгофа записываем два оставшихся уравнения (всего уравнений столько же, сколько токов): 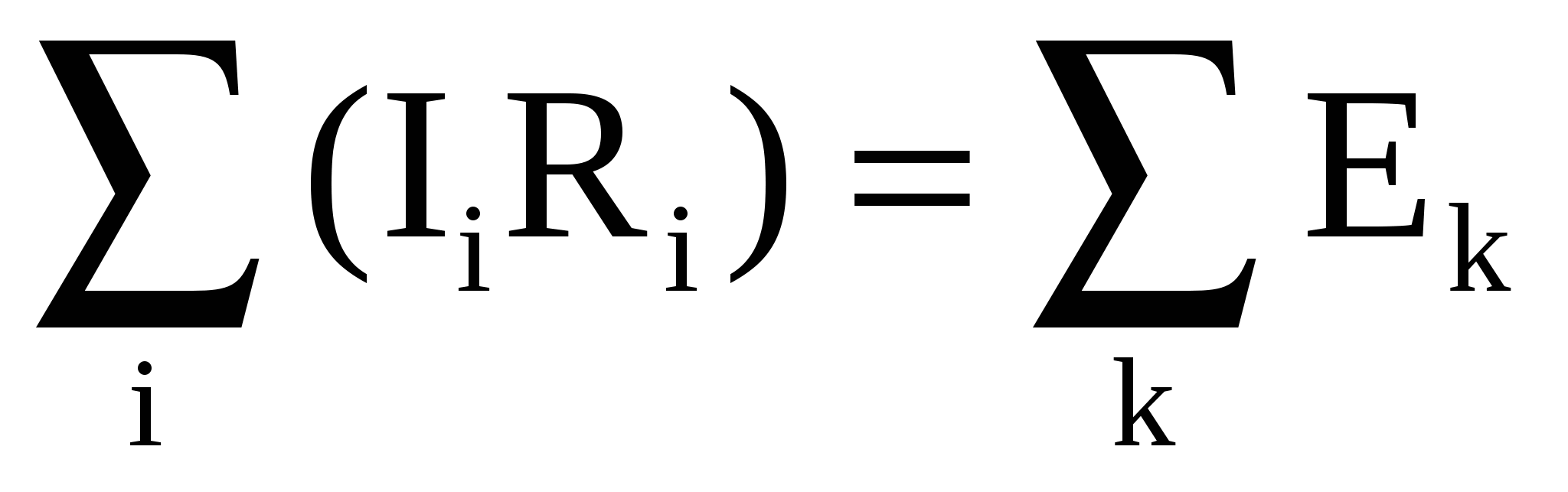 – алгебраическая сумма падений напряжений на сопротивлениях в любом замкнутом контуре равна алгебраической сумме электродвижущих сил. Здесь также нужно соблюдать правила знаков: если направление обхода контура на данном участке противоположно направлению тока, то падение напряжения берем с отрицательным знаком; если ЭДС проходим от плюса к минусу, то берем ее с отрицательным знаком. – алгебраическая сумма падений напряжений на сопротивлениях в любом замкнутом контуре равна алгебраической сумме электродвижущих сил. Здесь также нужно соблюдать правила знаков: если направление обхода контура на данном участке противоположно направлению тока, то падение напряжения берем с отрицательным знаком; если ЭДС проходим от плюса к минусу, то берем ее с отрицательным знаком.
|
Найти:
I3=?
U3=?
|
|
Таким образом, получим для контуров abef и abcdef:
I1R1+I2R2=E1 (2)
I1R1–I3R3=E1–E2. (3)
Решаем систему уравнений (1) – (3); из (1) получим:
I2=I1+I3, (4)
После подстановки (4) в (2) и замены в (2) и (3) известных величин на их численные значения:
3I1+2I3=1, (5)
I1–3I3=–4. (6)
Из (4): I1=3I3–4, после подстановки в(5):
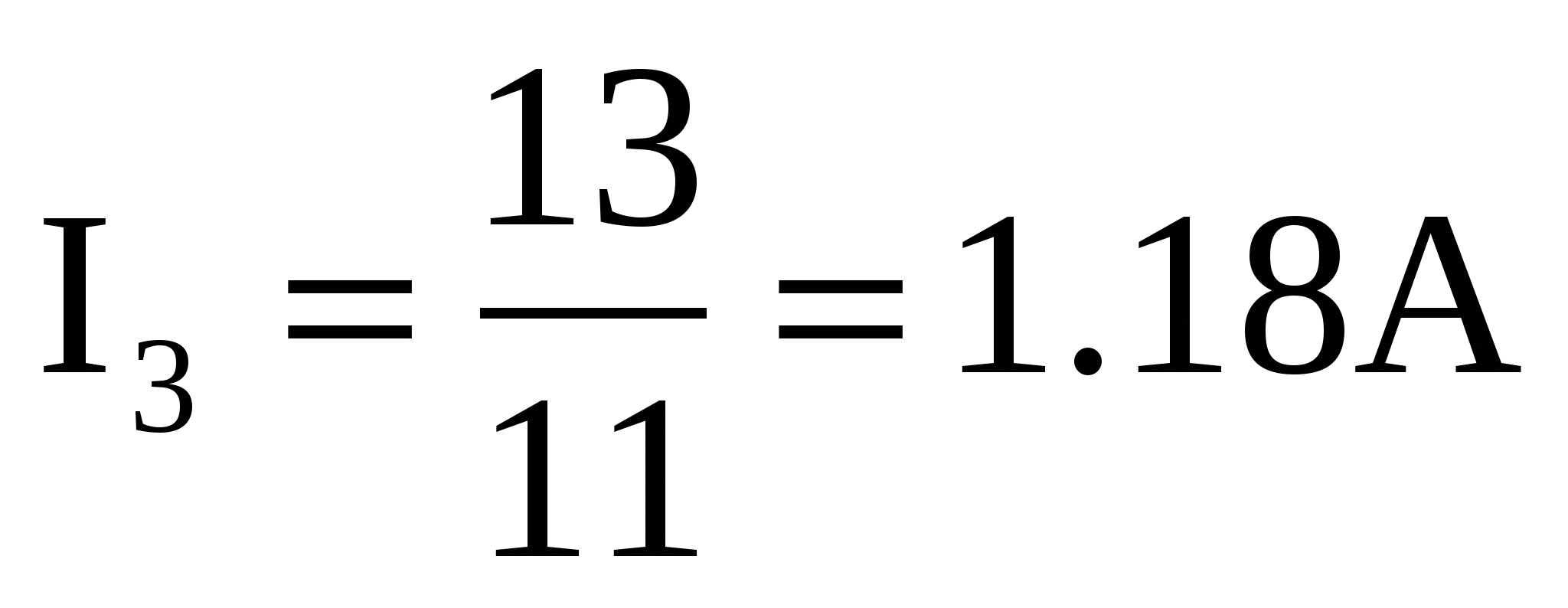 , ,
напряжение U3 найдем по закону Ома для участка цепи:
U3= I3R3=1.18.3=3.55 В.
|
Ответ: I3=1.18 А
U3= 3.55 В
|
Пример 8.
Сила тока в проводнике сопротивлением 12 Ом равномерно убывает от максимального значения до нуля за 10 с. Какое количество теплоты выделится в этом проводнике за указанный промежуток времени, если при этом по проводнику прошел заряд 50 Кл?
Дано:
R=12 Ом
t0=10 с
Δq=50 Кл
|
Решение:
Запишем закон, по которому изменяется со временем сила тока в проводнике. Ток убывает равномерно, то есть по линейному закону, от максимального значения I0, тогда:
I=I0–kt, (1)
где k – быстрота убывания тока:
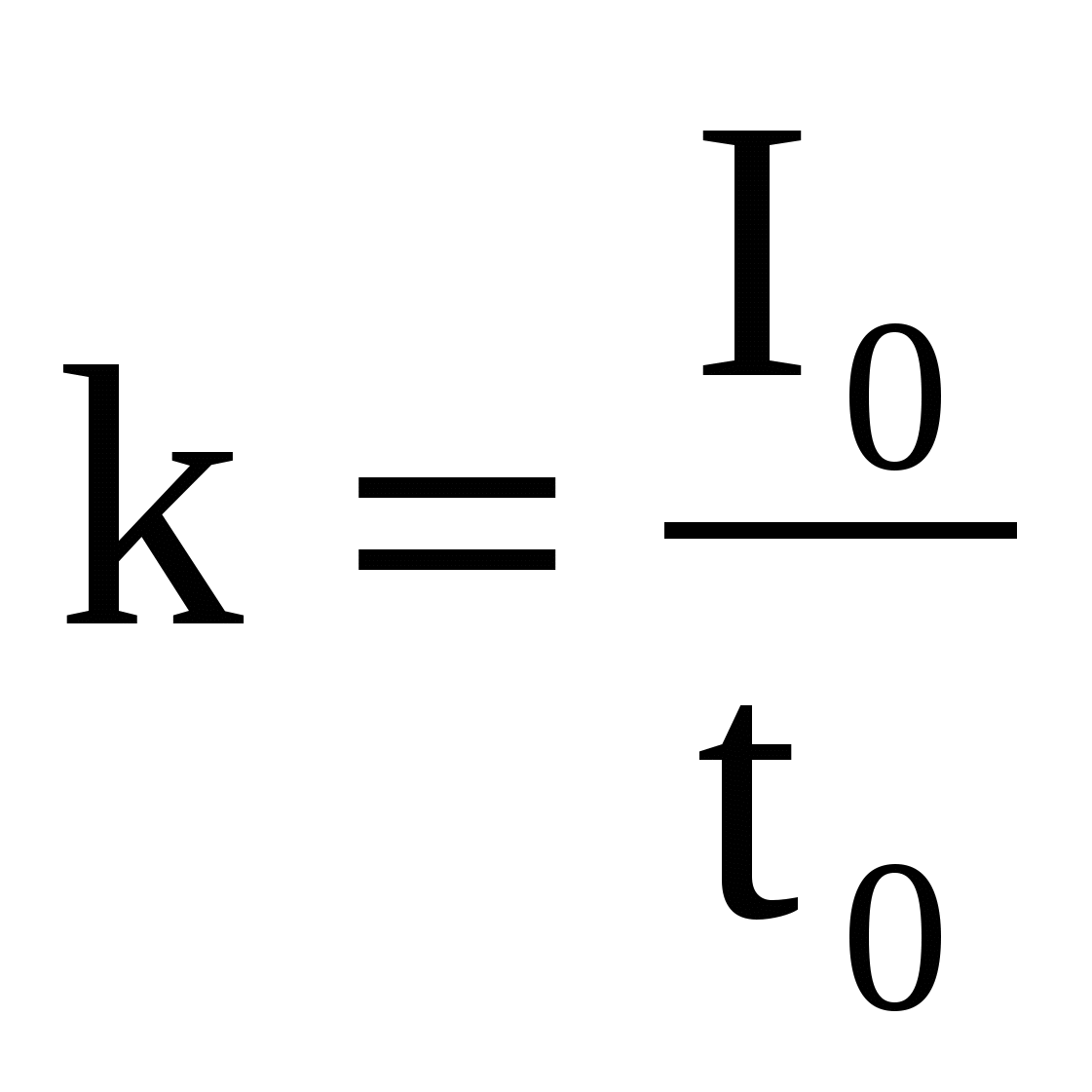 . (2) . (2)
Заряд, прошедший через сечение, можно рассчитать, интегрируя силу тока по времени в рассматриваемом промежутке: так как 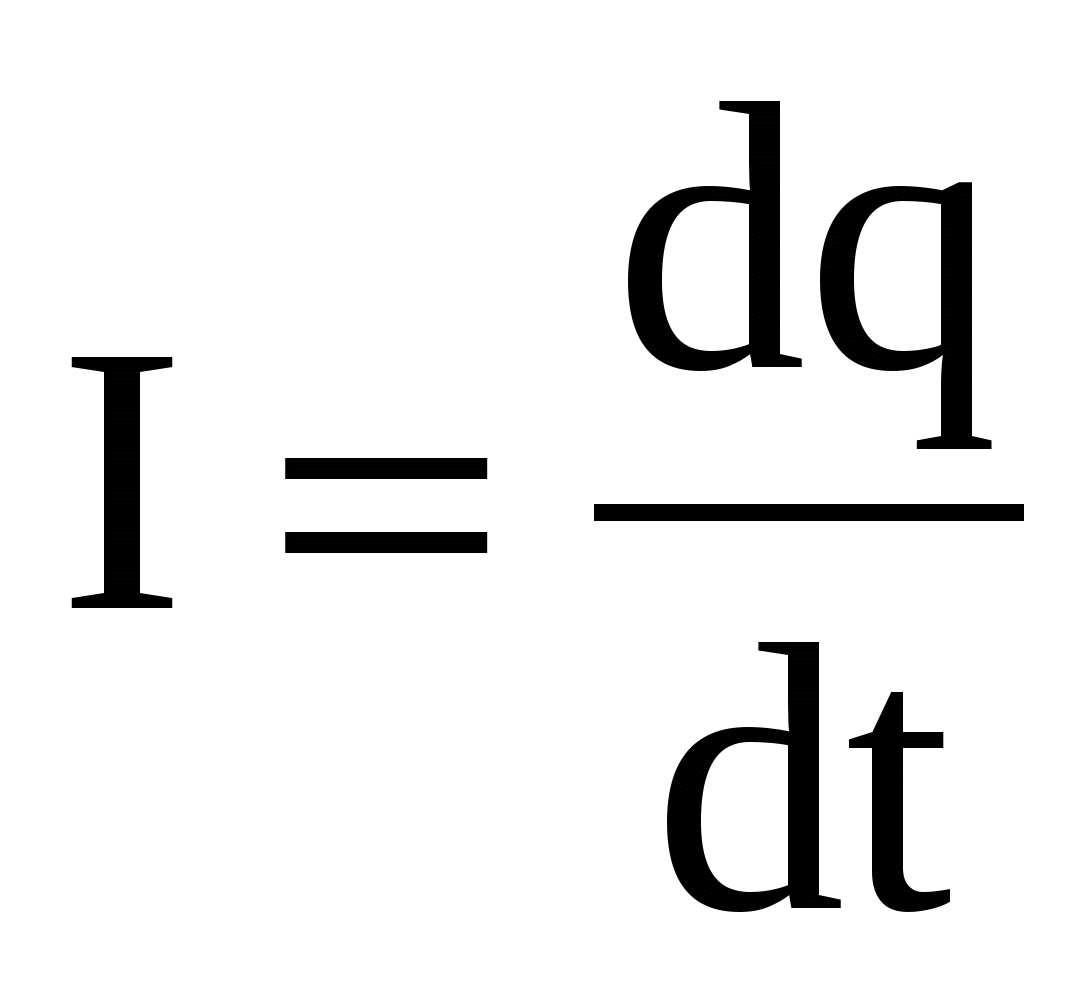 , то , то
 , ,
с учетом (2):
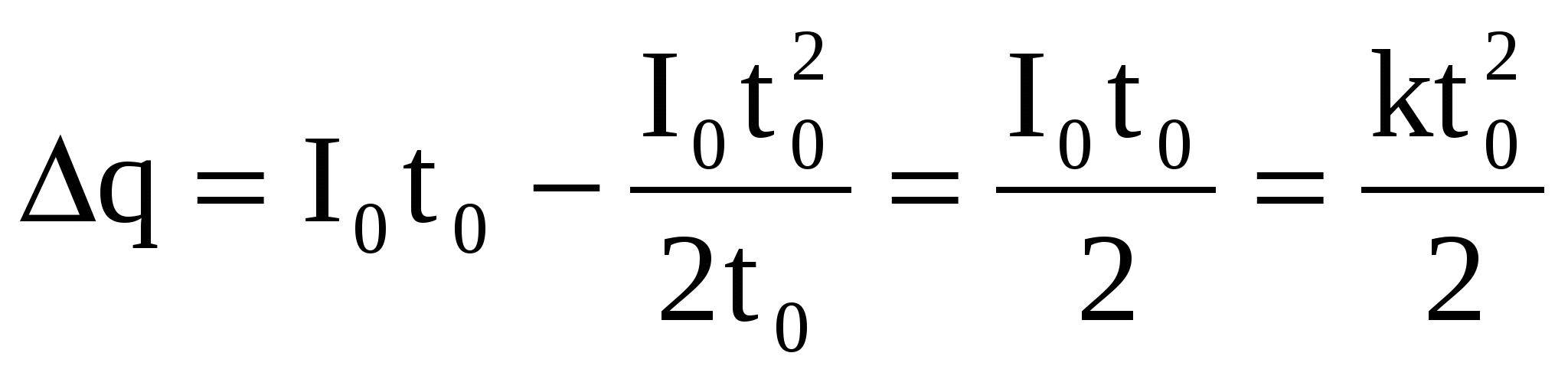 . (3) . (3)
|
Найти:
Q=?
|
|
Количество выделившейся теплоты находим по закону Джоуля-Ленца, подставив (1):
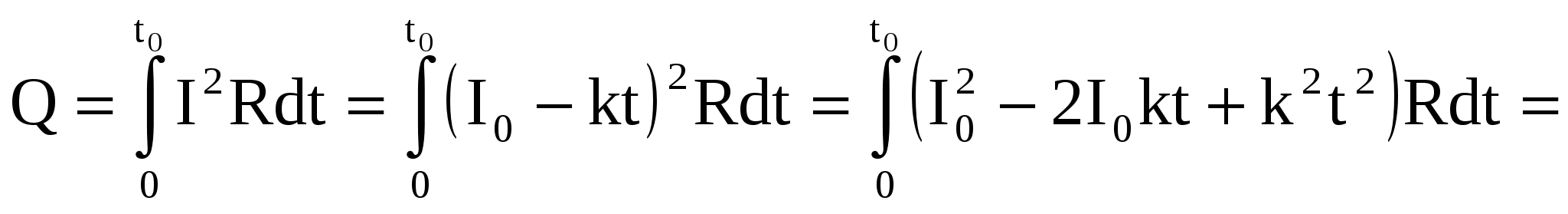
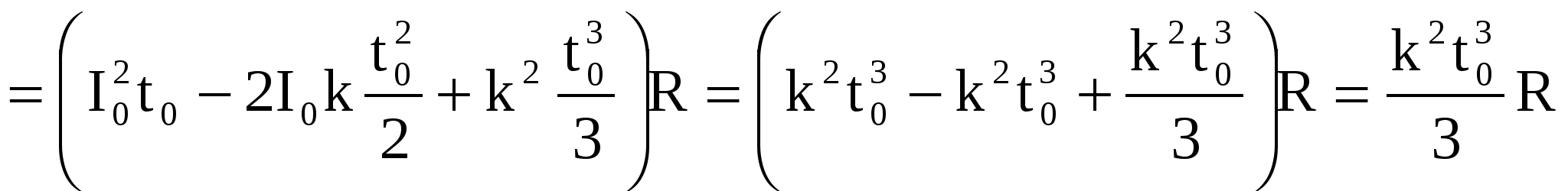 . (4) . (4)
Здесь учтено, что из (2) I0=kt0.
Из (3)  , тогда , тогда
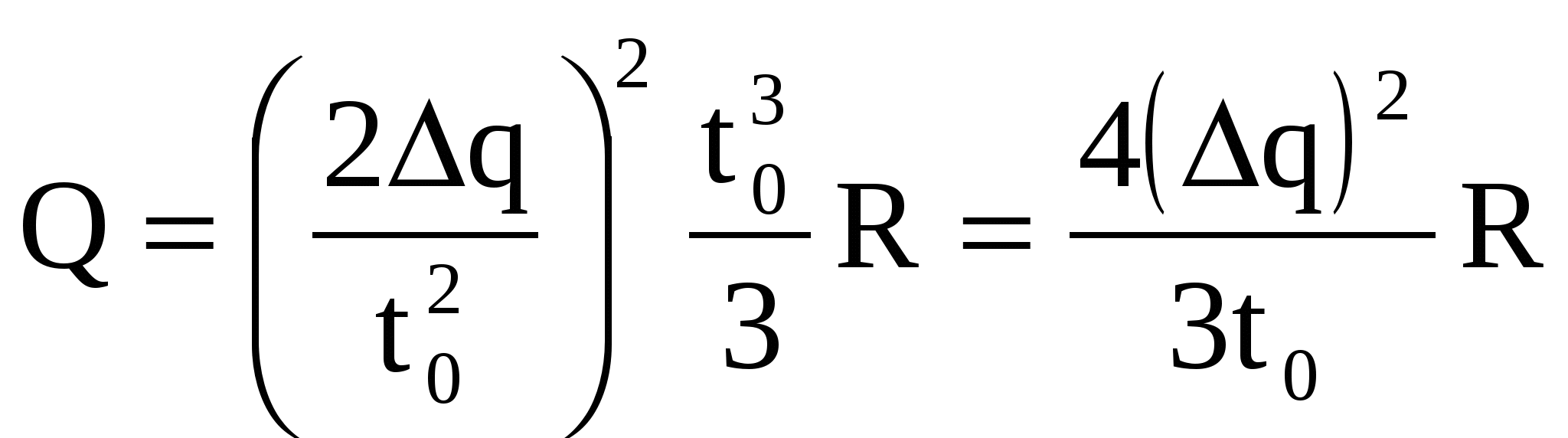 . .
Вычисляем:
 . .
|
Ответ: Q=4000 Дж
|
|
 Скачать 455 Kb.
Скачать 455 Kb.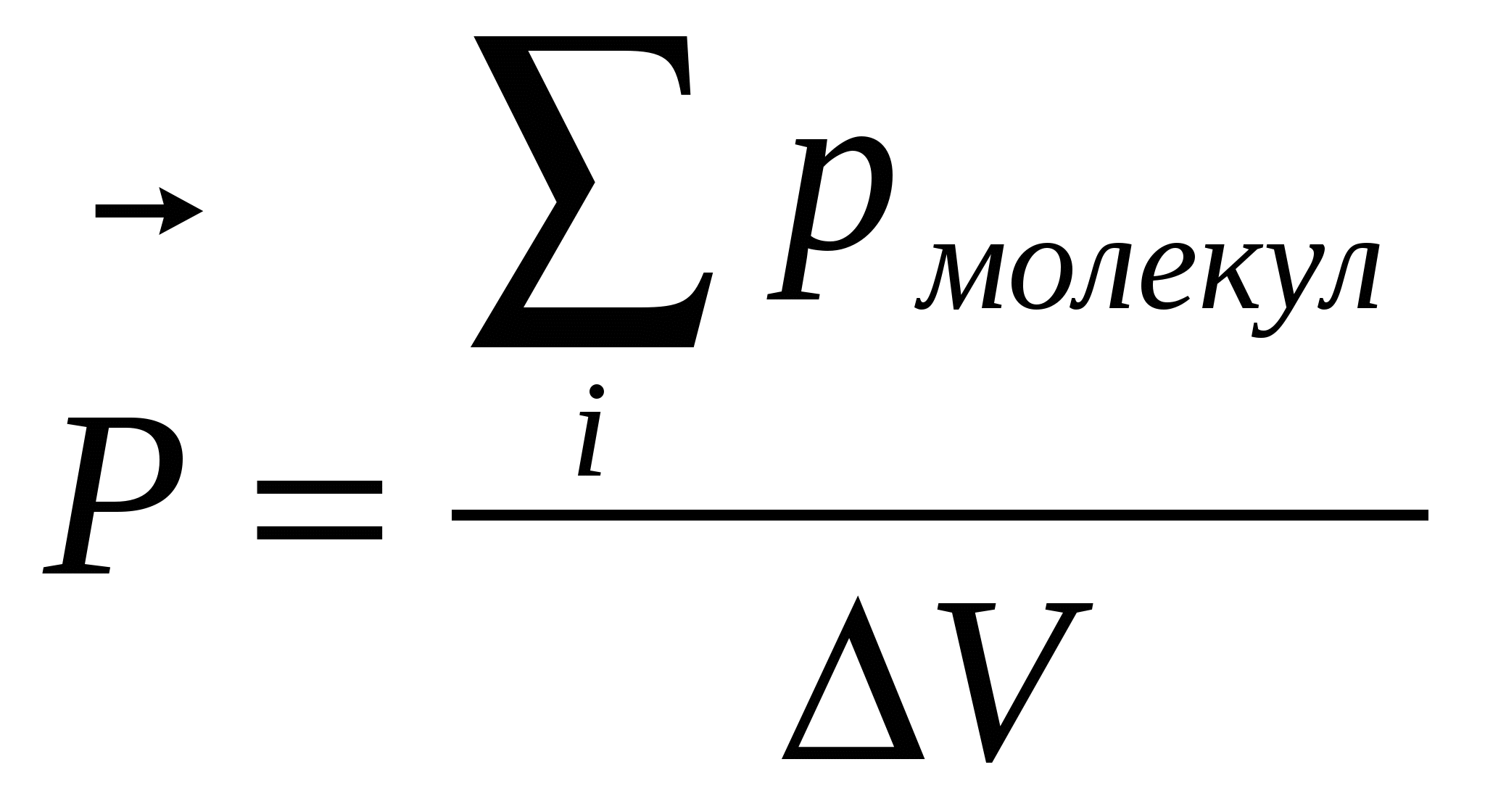 ,
,  пределить силу тока в сопротивлении R3 и напряжение на концах этого сопротивления. Е1=1 В, Е2=5 В, R1=1 Ом, R2=2 Ом, R3=3 Ом.
пределить силу тока в сопротивлении R3 и напряжение на концах этого сопротивления. Е1=1 В, Е2=5 В, R1=1 Ом, R2=2 Ом, R3=3 Ом.

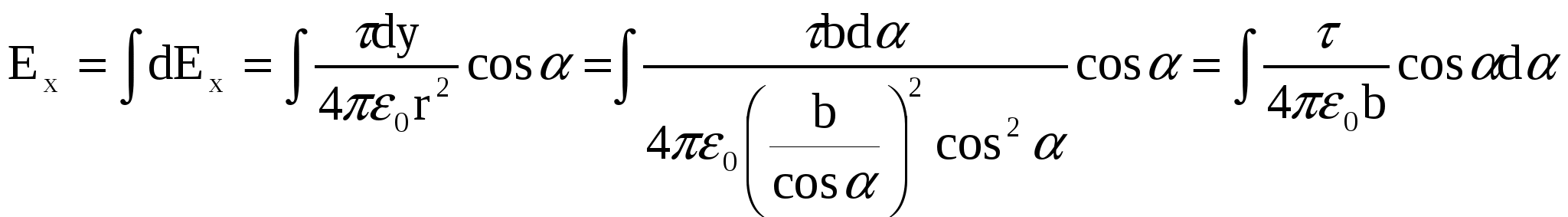 , (7)
, (7)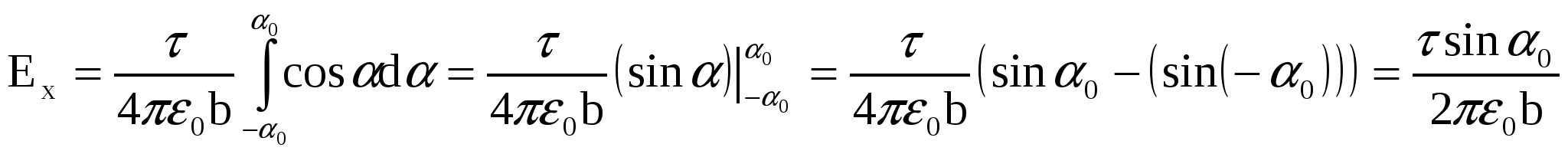 ,
,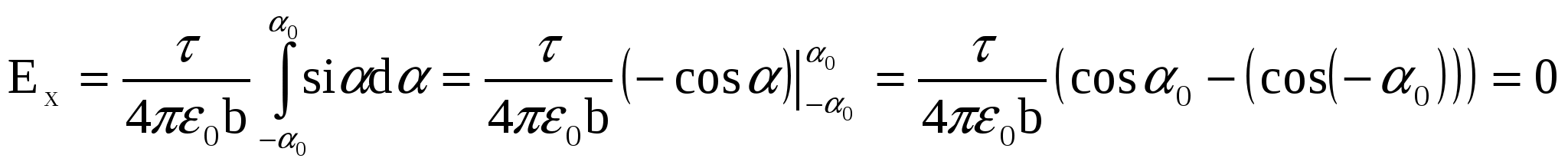 .
.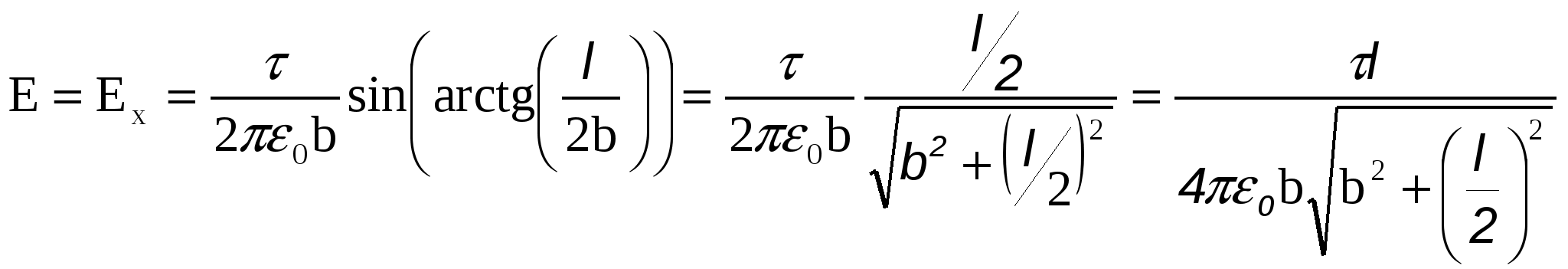 ,
, .
.
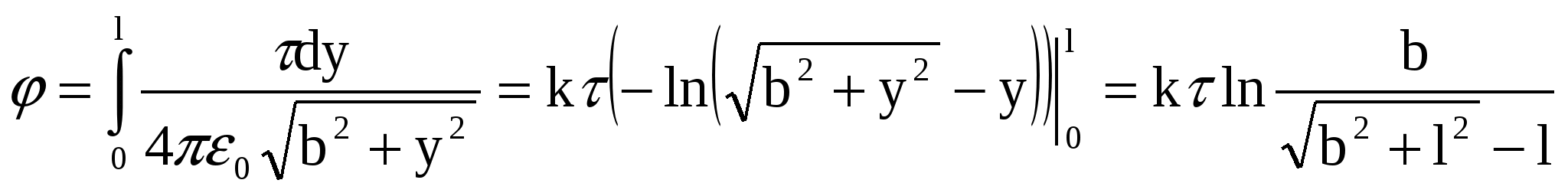 . (4)
. (4)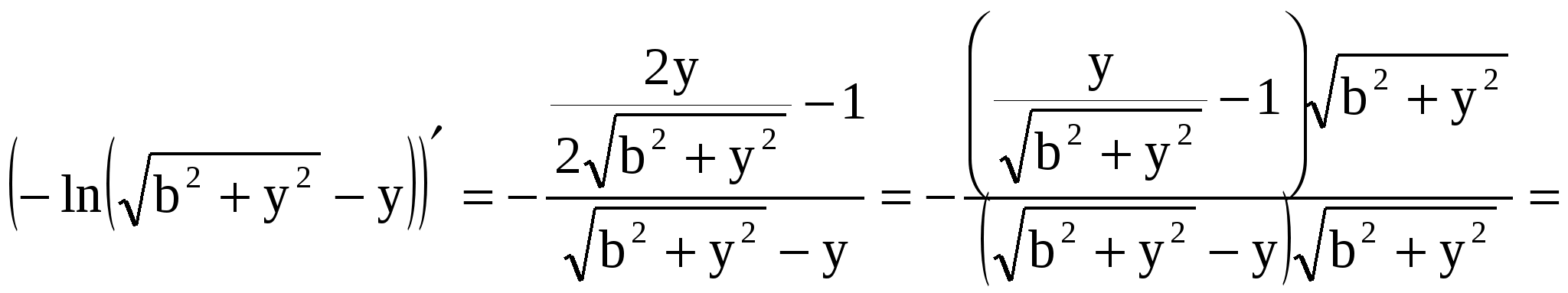


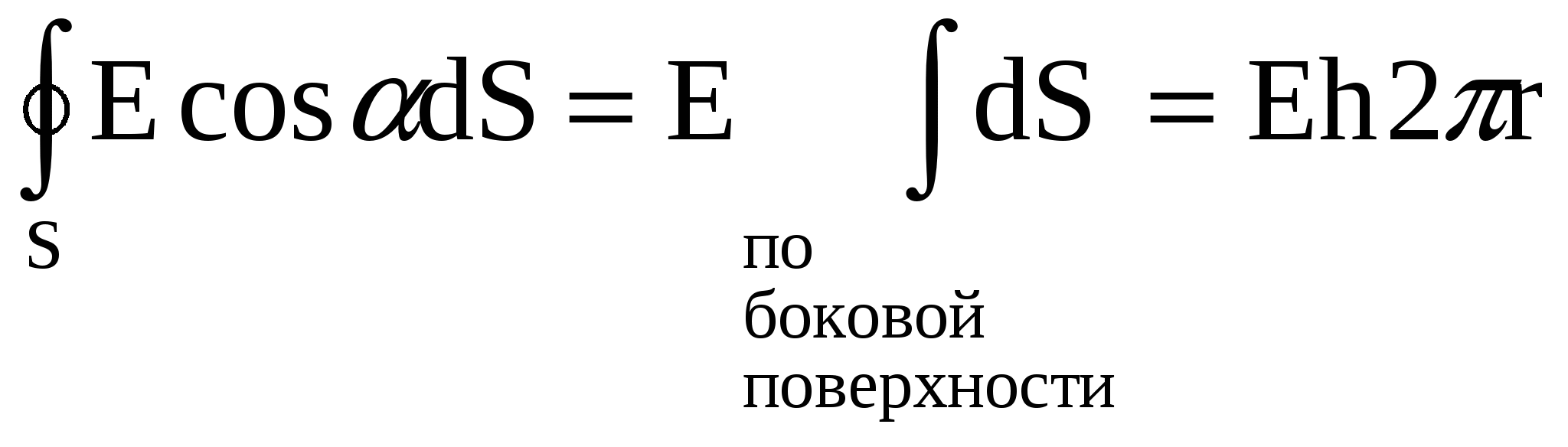 , (2)
, (2)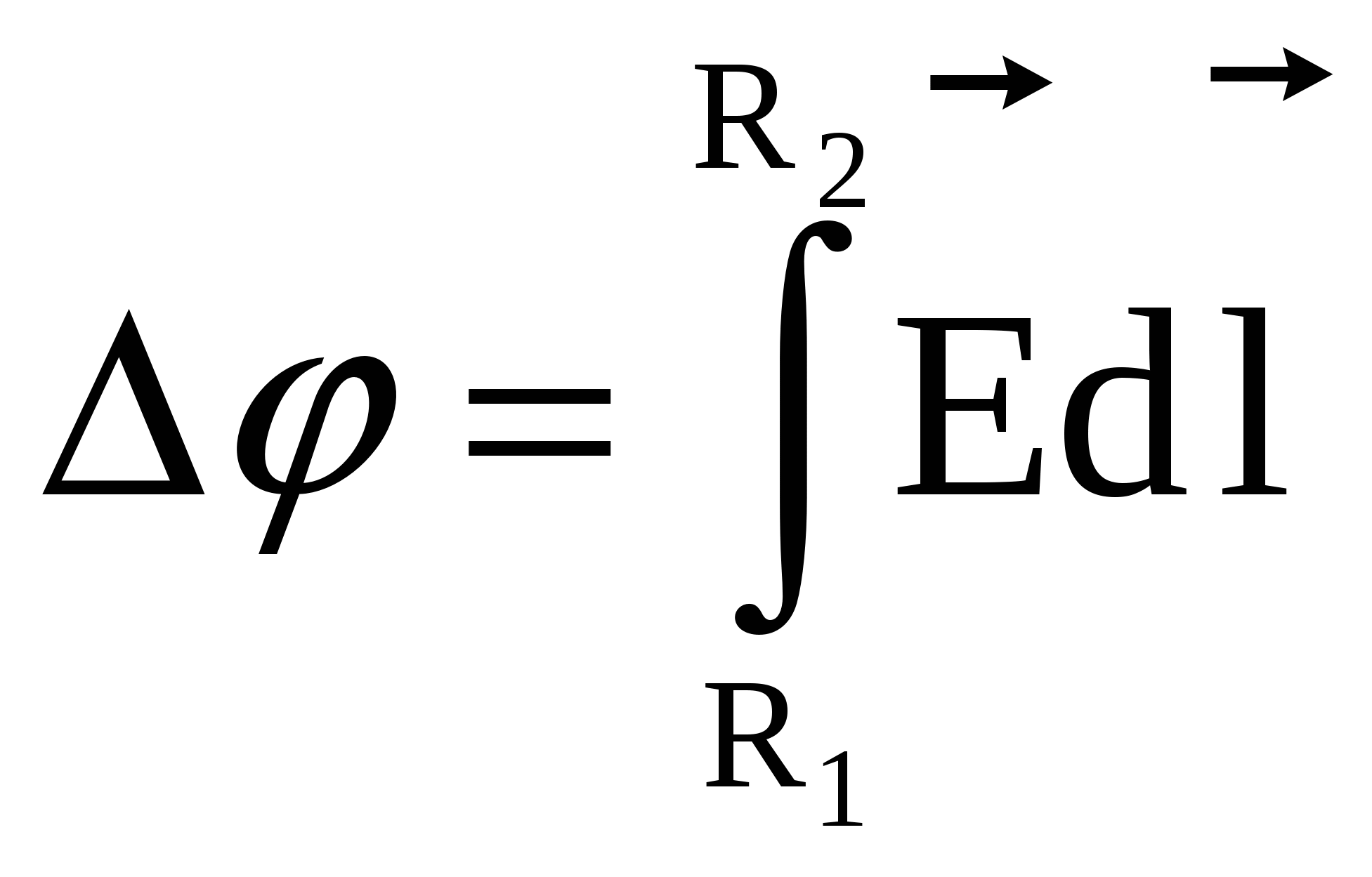 , (2)
, (2) ,
,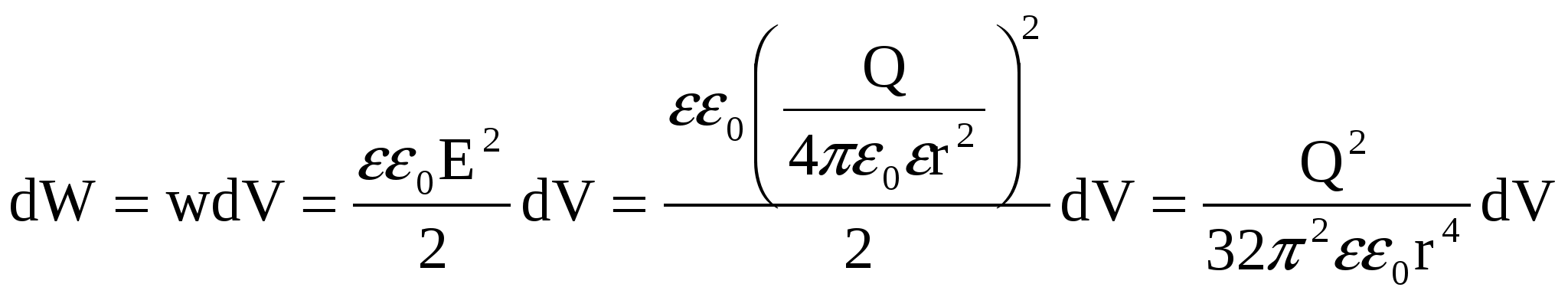 . (4)
. (4)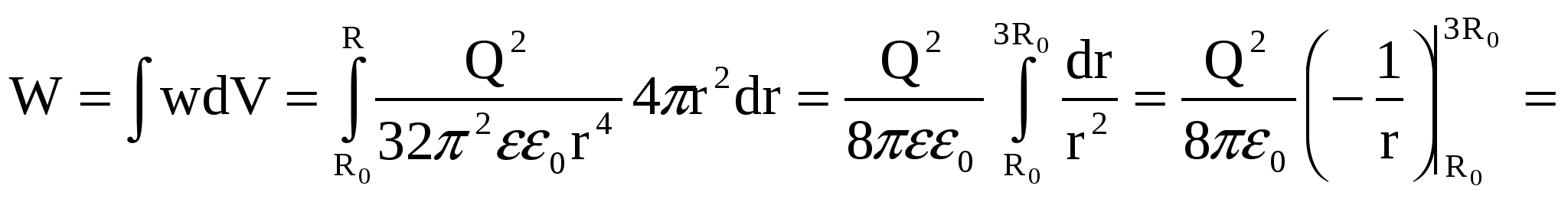



 ,
,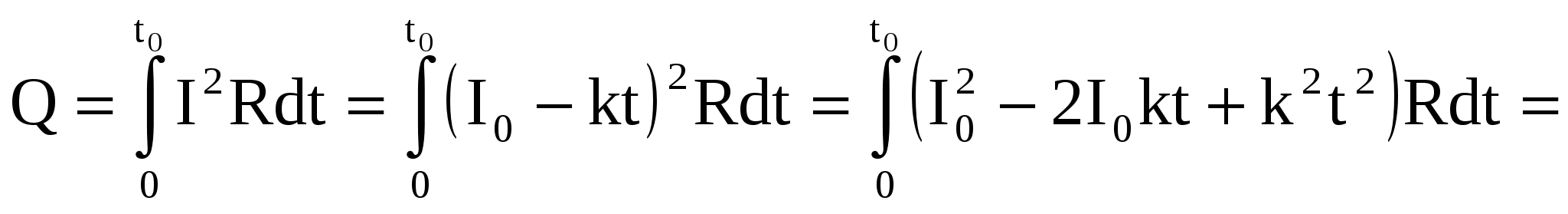
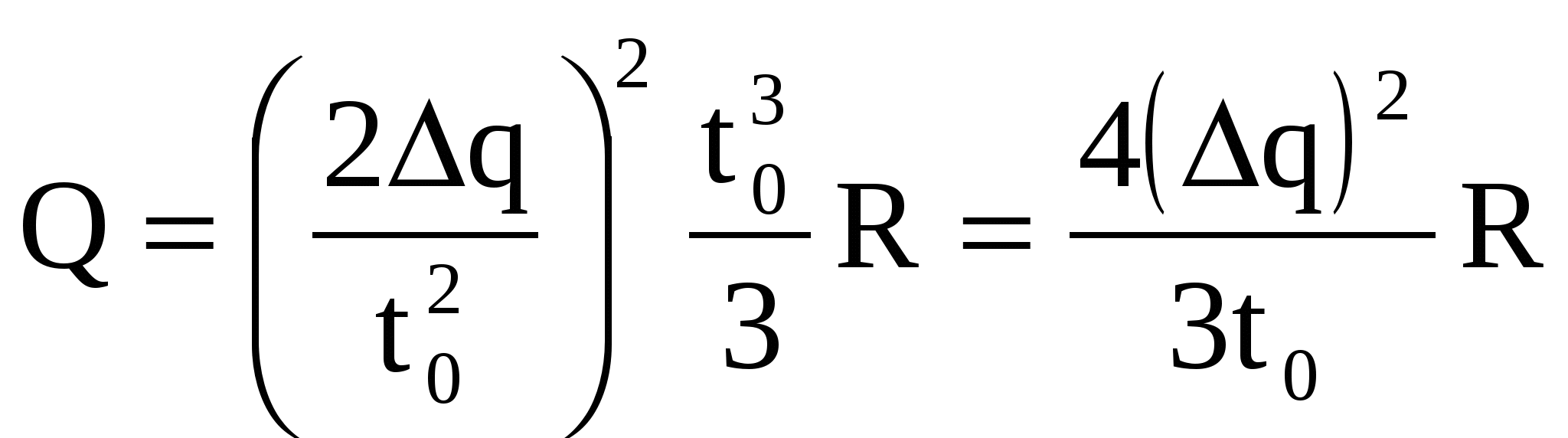 .
.