Закон Кулона. Запишите систему основных уравнений, описывающих электромагнитные взаимодействия в классическом контексте
 Скачать 48.93 Kb. Скачать 48.93 Kb.
|
|
1. ЭЛЕКТРОСТАТИКА 1.1.Электрический заряд. Закон Кулона. Запишите систему основных уравнений, описывающих электромагнитные взаимодействия в классическом контексте. Перечислите основные свойства электростатических взаимодействий между элементарными частицами и основные свойства электрических зарядов Выведите закон Кулона для точечных макроскопических зарядов из свойств электростатических взаимодействий элементарных частиц. Опишите основные системы единиц, используемые для описания электромагнитных явлений. Приведите пример расчета, использующего закон Кулона. Задачи, которые могут быть включены а экзаменационные билеты: К укрепленному неподвижно небольшому шарику с зарядом Q на нити длиной l подвешен небольшой шарик массой m, имеющий электрический заряд . Какую начальную горизонтальную скорость нужно сообщить подвешенному шарику и под каком углом следует отклонить нить для того, чтобы он начал равномерно вращаться по круговой траектории вокруг вертикальной оси, проходящей через точку подвеса, с периодом Т? В нижней точке пустоq шарообразноq полости радиусом R, сделанной в большом куске электронейтрального непровдящего материала, закреплен точечный заряд Q. Какой электрический заряд следует сообщить небольшому шарику массой m, помещенному внутрь этой полость, для того, чтобы он мог находиться в ее верхней точке в состоянии устойчивого равновесия? Не очень давно думали, что электрон в невозбужденном атоме водорода вращается округ заряженного весьма массивного и практически неподвижного ядра по круговой орбите подобно тому, как планета может вращаться вокруг звезды («планетарная модель атома водорода»). Считая, что радиус орбиты электрона атоме водорода равен 0.5А (1А = 10-10м), рассчитайте частоту вращения электрона вокруг ядра, скорость движения электрона по орбите и энергию ионизации атома водорода (минимальную энергию, которую нужно сообщить атому для того, чтобы он мог удалиться от ядра на бесконечно большое расстояние 1.2. Электрическое поле. Вектор напряженности электрического поля и его расчеты прямым суммированием 1. Закон Кулона и принцип суперпозиции для электрической силы, действующей на точечный заряд 2. Вектор напряженности электрического поля. Принцип суперпозиции для электрических полей. Изображение электрических полей с помощью силовых линий. Примеры 3. Электрическое поле как физический объект -переносчик взаимодействия. Аргументы «за» и «против» полевой концепции 4. Микроскопическое и макроскопическое электрическое поле. Объемная, поверхностная и линейная плотности зарядов. 5. Примеры вычисления полей простейших распределений зарядов прямым суммированием и интегрирования. Задачи, которые могут быть включены в билеты 1.2.1. Кольцо радиусом R равномерно заряжено по длине суммарным зарядом Q. По перпендикулярной плоскости кольца прямой, походящей через цент кольца, без трения может двигаться небольшой шарик массой m имеющий заряд q. Рассчитайте напряженной электрического поля в произвольной точке прямой и постройте график зависимости х-проекции напряженности поля от расстояния до центра кольца Найти массу малых колебаний частицы вблизи центра кольца. 1.2.2. Рассчитать напряженность электрического поля на высоте h над равномерно заряженной постоянной поверхностной плотностью заряда σ плоскостью, выполняя суммирование а) по кольцам, в) по полоскам. 1.2.3. Доказать, что любой точки плоскости, перпендикулярной полубесконечной нити, равномерно заряженной линейной плотностью заряда и проходящей через точку обрыва нити, вектор напряженности электрического поля направлен под углом 45о к плоскости. Сказанное справедливо для всех точек плоскости, кроме точки касания ее нити. Скалярный потенциал Доказательство теорему о потенциальном характере центрального поля Вывод выражения для потенциальной энергии точечного заряда поле системы зарядов и определение потенциала. Расчет потенциала точечного заряда относительно бесконечно удаленной очки и запись выражений для потенциалов, создаваемых дискретными и непрерывными распределениями зарядов. Расчет напряженности поля по известному потенциалу. Пример на расчет электрического потенциала, создаваемого ограниченным распределением зарядов и соответствующей напряженности электрического поля. Задачи, которые могут быть включены в билеты 1.3.1. В центре неподвижного равномерно заряженного зарядом Q диска радиусом R приклеен небольшой шарик массой m, имеющий заряд q того же знака, что и заряд диска. Клей испаряется и заряд начинает улетать от диска. Найти скорости шарика и диска в далеком будущем, когда указанные тела разлетятся на очень большое расстояние друг от друга. 1.3.2. Найти электрический потенциал во всех точках пространства, где покоится равномерно заряженная по поверхности зарядом Q сферы радиуса R. Найти потенциал в произвольной точке пространства, если потенциал бесконечно удаленной точки равен нулю. Рассчитать соответствующее найденному потенциалу пространственное распределение напряженности электрического поля. 1.3.3. Рассчитать пространственное распределение потенциала и напряженности электрического поля электрического диполя и его двумерного аналога (двух близкорасположенных разноименно заряженных бесконечных нитей). 1.4. Интегральная форма записи уравнений электростатики вакуума 1. Определения основных интегральных характеристик векторных полей: потока и циркуляцию 2. Формулировка и доказательство теоремы о циркуляции вектора напряженности электростатического поля. 3. Формулировка и доказательство теоремы Гаусса о потоке векторного поля 4. Полуклассическая оценка частоты колебаний мюона внутри ядра 5. Аналогии между уравнениям электростатики и гравитационной статики. Примеры использование аналогий между электростатикой и классической теории гравитации при решении задач. Задачи, которые могут быть включены в экзаменационные билеты 1.4.1. Рассчитайте для всех точек пространства электростатические поля и соответствующие потенциалы и постройте графики для следующих симметричных распределений зарядов: 1. Однородный шар радиусом R, равномерно заряженный по объему плотностью зарядоа . 2.Однородный шар радиусом R равномерно заряженный по поверхности зарядом Q 3. Однородный круговой бесконечный цилиндр радиуса R, равномерно заряженный по объему постоянной плотноcтью заряда ρ 4. Однородный круговой бесконечный цилиндр радиуса R, равномерно заряженный по поверхности поверхностной плотностью заряда σ. 5. Однородный бесконечный равномерно заряженный по объеме толщиной d 1.4.2. Рассчитайте период колебаний точечно частицы массой m с зарядом +q внутри неподвижного равномерно заряженного противоположным зарядом -Q облака радиусом R. 1.4.3. После прыжка через подпространство космические путешественники оказались вблизи планеты Гравигауссии, представляющей собой длинный однородный круговой цилиндр, равномерно вращающийся вокруг своей оси. Сутки на Гравигауссии длятся T, а на поверхности – невесомость. Найти плотность вещества, из которого сделана Гравигауссия. 1.5. Дифференциальная форма записи уравнений электростатики вакуума 5.1. Вывод дифференциального аналога интегральной теоремы о потоке вектора Е 5.2. Обоснование возможности обратного перехода от дифференциальной формулировки к интегральной. Понятие о теореме Гаусса-Остроградского 5.3. Вывод дифференциального аналога теоремы о циркуляции вектора Е. 5.4. Оператор Лапласа. Вывод уравнения Пуассона для электрического потенциала. 5.5. Аналогии между уравнениями электростатики и гравитационной статики. Примеры использование аналогий между электростатикой и классической теории гравитации при решении задач. Задачи, которые могут быть включены в экзаменационные билеты Вычислить дивергенцию вектора R . Вычислить ротор вектора R Придумайте векторное поле Х, для которого rotX = 5 1.6. Электростатическое поле при наличии проводников 6.1. Формулировка и обоснование основных электростатических свойств проводников и вектора Е при их наличии. 6.2. Формулировка и доказательство теоремы единственности решения задач электростатики в области, на границе которой задан потенциал. 6.3. Метод изображений. Пример использования для задач на расчет поля вблизи полубесконечного проводника с плоской границей. 6.4. Метод изображений. Пример использования для задач на расчет поля вблизи заземленного (или электрически нейтрального) проводящего шара (или цилиндра). 6.5. Метод изображений. Пример использования для задач на расчет распределения заряда на поверхности проводящего шара (или цилиндра), помещенного в однородное электростатическое поле Задачи, которые могут быть включены в экзаменационные билеты Точечный заряд q расположен на высоте h над бесконечной проводящей плоскостью. Найти величину полного заряда, индуцированного на плоскости. Электрический диполь расположен на высоте h над бесконечной проводящей плоскостью так, что его дипольный момент d перпендикулярен ей. Найти силу, действующую на диполь. Какой заряд нужно сообщить первоначально нейтральной проводящей сфере радиусом R для того, чтобы расположенный на расстоянии L от ее центра точечный заряд q не испытывал действия электрических сил? Равномерно заряженная нить с заданной плотностью заряда расположена параллельно бесконечному проводящему цилиндру с нулевым зарядом. Найти силу, действующую на единицу длины нити. Бесконечный проводящий цилиндр радиусом R помещен в однородное электрическое поле напряженностью Е так, что его ось перпендикулярна линиям поля. Найти распределение наведенного заряда на поверхности цилиндра. Найти силу, разрывающую по экватору металлический шар радиусом R, заряженный зарядом Q. 1.7. Механизмы поляризации диэлектриков 7.1. Мультипольное разложение и классификация молекул по их электрическим свойствам 7.2. Понятие поляризуемости молекулы (линейной и нелинейной) 7.3. Механизм электронной поляризации и расчет поляризуемости атома Томсона. 7.4. Механизм ориентационной поляризации и расчет средней ориентационной поляризуемости для газа из жестких диполей. 7.5. Тензор поляризуемости анизотропных молекул Задачи, которые могут быть включены в экзаменационные билеты Рассчитать силу взаимодействия между ионом q и электрическим диполем с моментом d, находящимся ан расстоянии , находящимся на расстоянии R от иона. Дипольный момент направлен по прямой соединяющий ион и диполь. Рассчитать силу взаимодействия между ионом q и нейтральной молекулой с заданной поляризуемостью , находящимся на расстоянии R от иона. Рассчитать силу взаимодействия между нейтральной молекулой с заданной поляризуемостью и электрическим диполем с моментом d, находящимся на расстоянии R молекулы. Дипольный момент направлен по прямой соединяющий молекулу и диполь. Рассчитать силу взаимодействия между двумя диполями с заданными моментами d, находящимся на расстоянии R друг от друга. Дипольные моменты направлены по прямой соединяющий диполи. 1.8. Описание электростатических полей в диэлектриках при помощи векторов Е и D 8.1. Вектор поляризации P: определение и теорема с доказательством о его дивергенции. 8.2. Введение вектора D и получение соотношений для его дивергенции и потока 8.3. Связь между векторами Е и D, диэлектрическая проницаемость вещества 8.4. Условия для векторов Е и D на границе двух диэлектрических сред. 8.5. Пример вычисления электрического поля в диэлектрике с помощью теоремы о потоке вектора D. Задачи, которые могут быть включены в экзаменационные билеты Металлический шар радиусом R, заряженный положительным зарядом +Q, окружен сферической «шубой» (слоем) из однородного изотропного диэлектрика с диэлектрической проницаемостью ε=2, границы которого имеют радиусы 2R и 3R, вокруг которого имеется сферическая «шуба» из незаряженного проводника с границами 3R и 4R. Рассчитать величины векторов E и D во всех точках пространства, поверхностные заряды наведенные на всех границах сред и построить графики зависимостей от расстояния до центра шара величин E и D, а так же – потенциала. Решить задачу 8.1 для случая, когда «шубе» из проводника сообщили дополнительный свободный отрицательный заряд – Q/2. Решить задачу 8.1 для случая, когда «шубу» из проводника заземлили. Решить задачи 8.1 и 8.2 для случая проводников и «шуб» в виде соосных бесконечных цилиндров, для которых вместо зарядов заданы их линейные плотности. . 1.9. Примеры расчета электрических полей в диэлектриках 9.1. Использование теоремы о потоке вектора D для расчета электрических полей в диэлектриках в системах с высокой симметрией 9.2. Расчет электрического поле в случае точечного заряда q0, расположенного на высоте h над плоской границей полупространства, заполненного однородным изотропным диэлектриком с проницаемостью ε. 9.3. Электрическое поле, создаваемое однородно поляризованным шаром. 9.4. Расчет электрического поля внутри однородного диэлектрического шара с диэлектрической проницаемостью ε , помещенного в однородное электрическое поле Е0 9.5. Пример расчета электрических полей при наличии диэлектриков в случае задач с цилиндрической симметрией. Задачи, которые могут быть включены в экзаменационные билеты Рассчитать силу притяжения точечного электрического заряда q0, находящегося на высоте h над плоской границей полупространства из однородного изотропного диэлектрика с проницаемостью ε, к этому диэлектрику Рассчитать силу притяжения электрического диполя с моментом d, находящегося на высотеh над плоской границей полупространства из однородного изотропного диэлектрика с проницаемостью ε, к этому диэлектрику. Дипольный момент ориентирован перпендикулярно границе диэлектрика. Рассчитать силу, действующую на единицу длины бесконечной равномерно заряженной линейной плотностью заряда λ нити, находящегося на высотеh над параллельной ей плоской границей полупространства из однородного изотропного диэлектрика с проницаемостью ε. Рассчитать электрическое поле, создаваемое однородно поляризованным бесконечным цилиндром во всем пространстве. Вектор поляризации P направлен перпендикулярно оси цилиндра. Бесконечный цилиндр из однородного изотропного диэлектрика с проницаемостью ε помещен во внешнее однородное электрическое поле Е0так, что его ось перпендикулярна линиям исходного поля. Найти напряженность поля внутри цилиндра. 1.10. Поляризация конденсированных диэлектриков 10.1. Связь между векторами Е, Р и D в случае диэлектриков в виде разреженных газов 10.2. Различия между макроскопическим и микроскопическим полем в диэлектрике. 10.3. Расчет электрического поля однородно поляризованного шара. 10.4. Связь между векторами Р и Е в конденсированных изотропных диэлектрических средах. 10.5. Спонтанная электрическая поляризация вещества Задачи, которые могут быть включены в экзаменационные билеты Получить выражение, связывающее диэлектрическую проницаемость (коэффициент пропорциональности между векторами D и Е) с поляризуемостью молекулы в случае конденсированных изотропных диэлектриков 1.11. Электростатическая энергия 11.1. Обоснование формулы для потенциальной энергии системы неподвижных электрических зарядов. 11.2. Электростатическая энергия заряженного проводника. 11.3. Обоснование пропорциональности между зарядом и потенциалом проводника, введение емкости. Три формулы для энергии заряженного проводника 11.4. Взаимная емкость двух проводников. Конденсатор. Емкость и энергия плоского конденсатора 11.5. Емкости сферического и цилиндрического конденсаторов. Задачи, которые могут быть включены в экзаменационные билеты Рассчитать емкость сферического конденсатора, представляющего собой две концентрические сферы радиусами R1 R2 с однородным диэлектриком с заданной ε между ними. Рассчитать емкость цилиндрического конденсатора, представляющего собой два соосных цилиндра радиусами R1 R2 с однородным диэлектриком с заданной ε между ними. Плоский конденсатор состоит из двух параллельно расположенных проводящих обкладок в виде дисков радиусами R, расположенных на расстоянии h друг от друга. Рассчитать емкость конденсатора, если помещенный между обкладок конденсатора диэлектрик изменяет свою проницаемость от ε1 до ε2 по линейному закону в направлении от центра конденсатора до его края. Плоский конденсатор состоит из двух параллельно расположенных проводящих обкладок в виде дисков радиусами R, расположенных на расстоянии h друг от друга. Рассчитать емкость конденсатора, если помещенный между обкладок конденсатора диэлектрик изменяет свою проницаемость от ε1 до ε2 по линейному закону в направлении от одной обкладки к другой. Получить формулы для вычисления эффективной емкости батареи из двух конденсаторов с емкостями С1 и С2, соединенных между собой параллельно. Получить формулы для вычисления эффективной емкости батареи из двух конденсаторов с емкостями С1 и С2, соединенных между собой последовательно. Найти входную емкость «бесконечной лестницы» конденсаторов, изображенной на рисунке. 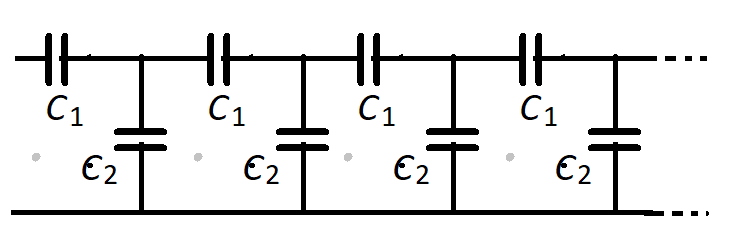 1.12. Объемная плотность энергии 12.1. Получение выражения для объемной плотности электрического поля в вакууме для частного случая плоского конденсатора 12.2. Обоснование выражения для объемной плотности электрического поля в вакууме в общем случае. 12.3. Работа по поляризации анизотропной молекулы. 12.4. Вывод соотношения для объемной плотности электрического поля в веществе. 12.5. Энергия, запасенная в поле электрически заряженного шарика. Классический радиус электрона. Задачи, которые могут быть включены в экзаменационные билеты Шарик радиусом R равномерно заряжен по объему. Во сколько раз отличается энергия, запасенная вне шарика от энергии, запасенной внутри него? 2. МАГНИТОСТАТИКА 2.1.Электрическое поле движущегося заряда Запишите основные релятивистские законы преобразований времени и длин отрезков и обоснуйте их (см. курс механики). Дайте определение величины движущегося заряда и сформулируйте основные свойства так определенного заряда (включая его соответствие электростатическому описанию). Обоснуйте вид релятивистских преобразований для компонент элекрического поля Получите выражение для электрического поля точечного заряда в случае его равномерного прямолинейного движения. Опишите конфигурацию поля равномерно двигавшегося и резко затормозившего заряда.. Задачи, которые могут быть включены а экзаменационные билеты: Получите зависимость величины (модуля) напряженности электрического поля движущегося заряда от угла между вектором его скорости и направлением на наблюдателя. Покажите, что несмотря на то, что напряженность электрического поля в направлении, перпендикулярном вектору скорости релятивисткой частицы, стремится к бесконечности при приближении скорости к световой, переданный таким зарядом импульс другой закрепленной заряженной частицы не возрастает неограниченно и, следовательно, заряженные частицы в ускорителях не могут разрушать его стены из-за эффекта концентрации линий поля в плоскости, перпендикулярной скорости (о чем нередко говорят не слишком образованные противники теории относительности). Механизм возникновения магнитных взаимодействий Запишите основные релятивистские законы преобразований времени и длин отрезков. Обоснуйте релятивистский закон преобразования сил (см. курс механики). Получите выражение для силы, действующей на заряд, движущийся в электрическом поле неподвижных относительно наблюдателя зарядов. Покажите как релятивистский эффект изменения силы, действующий между двумя электрическими зарядами может быть истолкован как результат существования дополнительных магнитных взаимодействий, возникающих при движении зарядов относительно наблюдателя. На примере взаимодействия двух зарядов, летящих с одинаковыми скоростями, перпендикулярными проходящей через них прямой, продемонстрируйте соответствие между релятивистским описанием и классическими представлениями о существовании дополнительных магнитных взаимодействий, возникающих между движущимися зарядами. Задачи, которые могут быть включены а экзаменационные билеты: Релятивистская частица с массой покоя m0 и начальной скоростью v0< Решите задачу 2.2.1 для случая сопоставимой со скоростью света начальной скорости частицы. Классическое описание магнитных взаимодействий Опишите способ введения вектора магнитной индукции В (в рамках классического подхода), основанный на анализе силы, действующей на движущийся в магнитном поле заряд. Используя выражение для силы Лоренца (действующей на единичный движущийся в магнитном поле заряд ), получите выражение для силы Ампера (действующей на провод с током в магнитном поле). Опишите способ введения вектора магнитной индукции В (в рамках классического подхода), основанный на анализе силы, действующей на провод с током в постоянном магнитном поле. Используя выражение для силы Ампера (действующей на провод с током ), получите выражение для вращающего механического момента, действующего на рамку с током в постоянном магнитном поле. Опишите способ введения вектора магнитной индукции В (в рамках классического подхода), основанный на анализе момента силы, действующей на рамку с током в постоянном магнитном поле. Задачи, которые могут быть включены а экзаменационные билеты: Практически покоившаяся нерелятивистская частица массой m с зарядом q пролетает через область пространства с ускоряющей разностью потенциалов U (вылетает из «электронной пушки») и влетает в однородное магнитное поле, вектор В которого направлен перпендикулярно вектору скорости частицы. Найти радиус кривизны круговой траектории и частицы в однородном магнитном поле (принцип работы масс-спектрографа - физического прибора для анализа химического состава газов). Пучок электронов, вылетающий из расположенной внутри электронно-лучевой трубки (ЭЛТ) электронной пушки, на которую подана разность потенциалов U, приобрел в пушке высокую (но нерелятивистскую) скорость вдоль оси трубки и летит к экрану, расположенному на расстоянии L от выходного отверстия пушки. Из-за того, что ь электроны в пушке возникли в результате термоэмиссии, кроме практически одинаковой продольной скорости (определяется ускоряющей разностью потенциалов U) электроны имеют случайно распределенные поперечные скорости. Какое продольное магнитное поле В нужно создать в трубке для того, чтобы все электроны попали в одну точку экрана (пучок был сфокусирован)? Два параллельных рельса расположены на расстоянии L друг от друга и наклонены под углом α к поверхности Земли. На рельсах покоится проводящий стрежень массой М, коэффициент трения которого о рельсы равен μ. Магнитное поле Земли В направлено вертикально вверх (система помещена в магнитный полюс планеты). Какую разность потенциалов нужно приложить между рельсами для того, чтобы стержень сдвинулся с места? (модель линейного электродвигателя). Прямоугольная рамка размерами a Х b может вращаться вокруг неподвижной горизонтальной оси, проходящей через ее центр. К центру рамки прикреплена «стрелка» - перпендикулярный плоскости рамки однородный стержень длиной L и массой M. Система помещена в однородное магнитное поле с индукцией В, направленной горизонтально, перпендикулярно оси вращения рамки. На какой угол отклонится стрелка от вертикали, если по рамке потечет ток I? (модель амперметра). |
