ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ
И ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
§ 1. Первый закон Ньютона. Масса. Сила
Первый закон Ньютона: всякая материальная точка (тело) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит её изменить это состояние. Стремление тела сохранять состояние покоя или равномерного прямолинейного движения называется инертностью. Поэтому первый закон Ньютона называют также законом инерции.
Первый закон Ньютона выполняется только в инерциальных системах отсчёта. Инерциальной системой отсчета является такая система отсчета, относительно которой материальная точка, свободная от внешних воздействий, либо покоится, либо движется равномерно и прямолинейно.
Масса тела — физическая величина, характеризующая инерционные (инертная масса) и гравитационные (гравитационная масса) свойства материи.
Масса тела – скалярная величина. Опыт показывает, что если два тела с массами m1 и m2 соединить в одно, то масса m составного тела оказывается равной сумме масс m1 и m2 этих тел: m = m1 + m2.
Э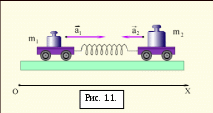 то свойство масс называют аддитивностью. то свойство масс называют аддитивностью.
Сравнение масс двух тел. 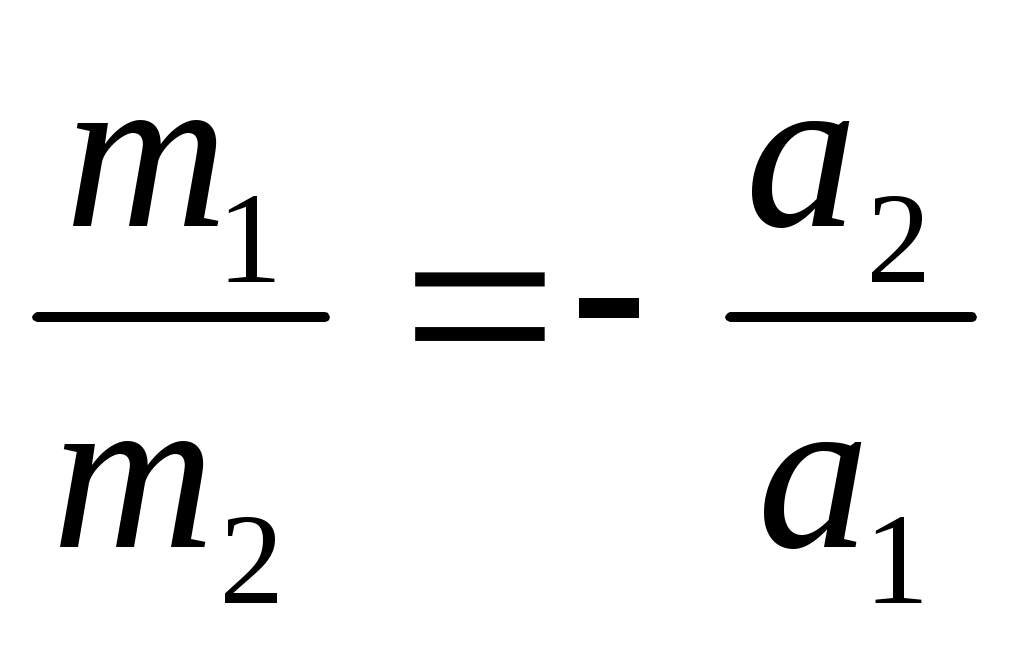
Сила — это векторная величина, являющаяся мерой механического воздействия на тело со стороны других тел или полей, в результате, которого тело приобретает ускорение или изменяет свою форму и размеры.
Для измерения сил используют откалиброванные пружины – динамометры. Сила измеряется по растяжению динамометра:
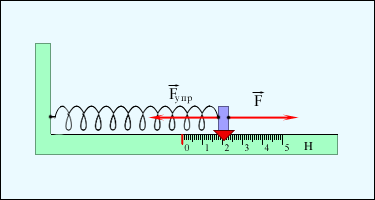
Рис. 1.2.
Измерение силы по растяжению пружины. При равновесии 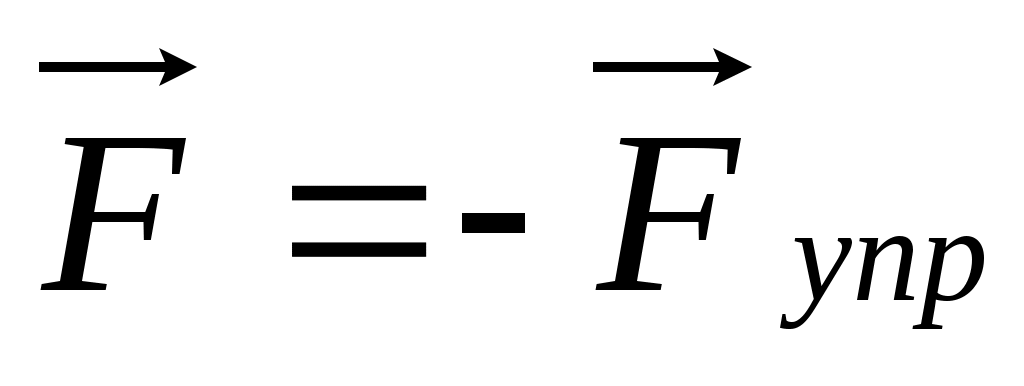 . .
§ 2. Второй закон Ньютона
Второй закон Ньютона — основной закон динамики поступательного движения — отвечает на вопрос, как изменяется механическое движение материальной точки (тела) под действием приложенных к ней сил.
Если рассмотреть действие различных сил на одно в то же тело, то оказывается, что ускорение, приобретаемое телом, всегда прямо пропорционально равнодействующей приложенных сил:
а F(т - const). (2.1)
При действии одной и той же силы на тела с разными массами их ускорения оказываются различными, а именно
а
1/m (F-const). (2.2)
Используя выражения (2.1) и (2.2) и учитывая, что сила и ускорение — величины векторные, можем записать
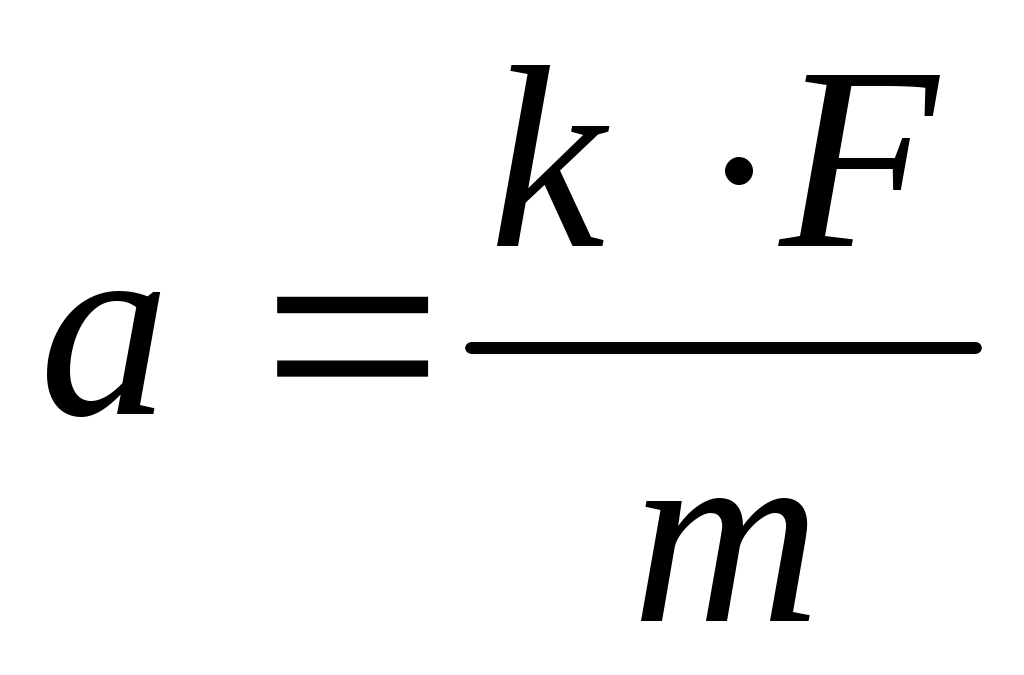 (2.3) (2.3)
Соотношение (2.3) выражает второй закон Ньютона: ускорение, приобретаемое материальной точкой (телом), пропорционально вызывающей его силе, совпадает с нею по направлению и обратно пропорционально массе материальной точки (тела).
В СИ коэффициент пропорциональности k= 1. Тогда
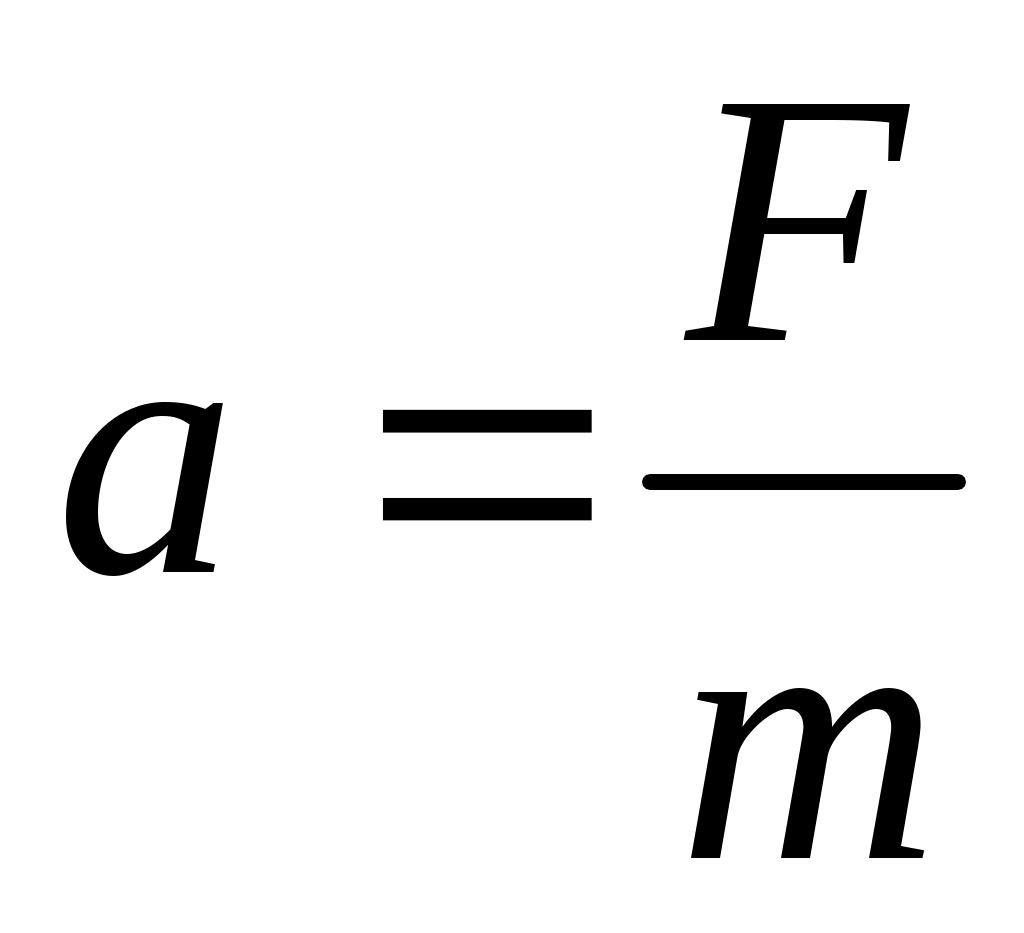
или  (2.4) (2.4)
Учитывая, что масса материальной точки (тела) в классической механике есть величина постоянная, в выражении (2.4) её можно внести под знак производной:
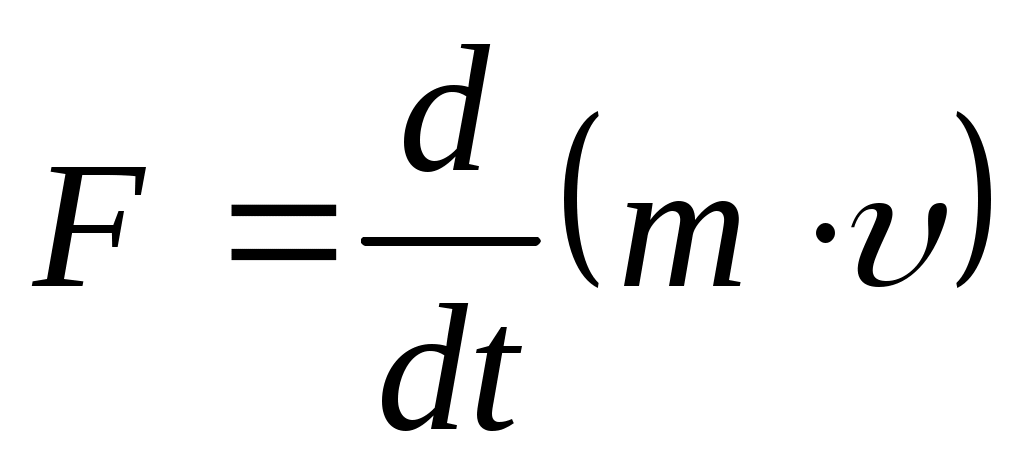 (2.5) (2.5)
Векторная величина
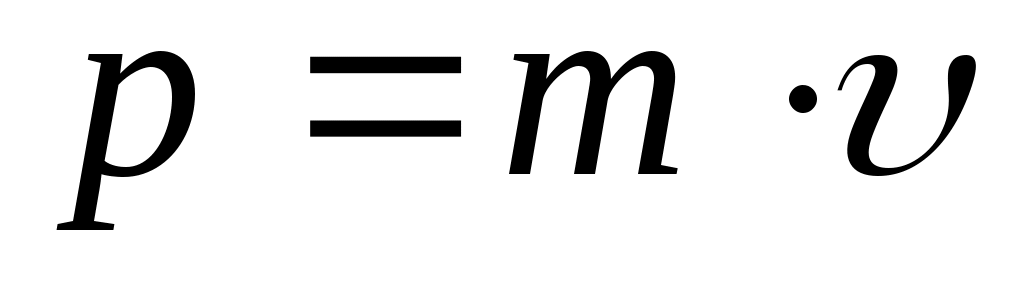 (2.6) (2.6)
называется импульсом (количеством движения) этой материальной точки.
Подставляя (2.6) в (2.5), получим
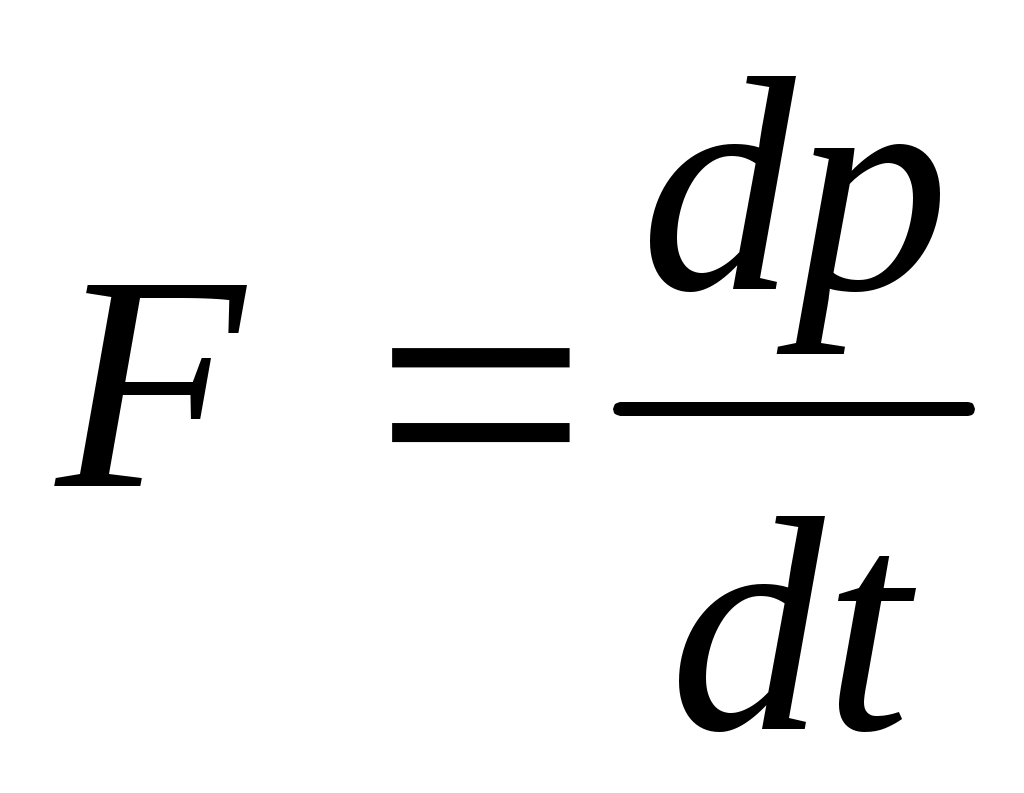 (2.7) (2.7)
Это выражение называется уравнением движения материальной точки.
Единица силы в СИ — ньютон (Н): 1 Н — сила, которая массе 1 кг сообщает ускорение 1 м/с2 в направлении действия силы:
1 Н= 1 кгм/с2.
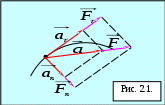
На рис. 2.1. действующая сила 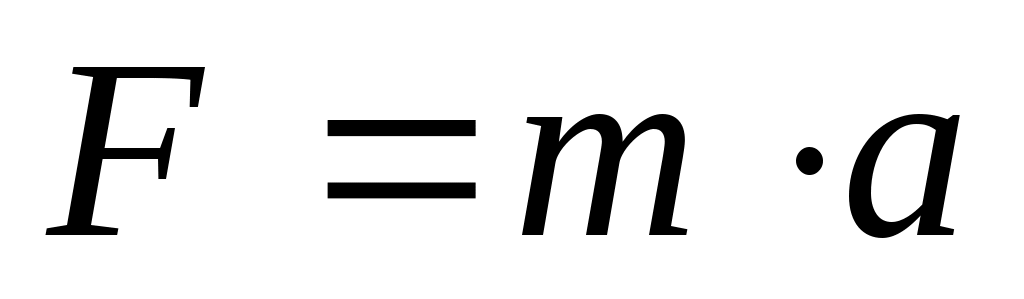 разложена на две составляющие: тангенциальную силу F (направлена по касательной к траектории) и нормальную Fn(направлена по нормали к центру кривизны).Используя выражения разложена на две составляющие: тангенциальную силу F (направлена по касательной к траектории) и нормальную Fn(направлена по нормали к центру кривизны).Используя выражения 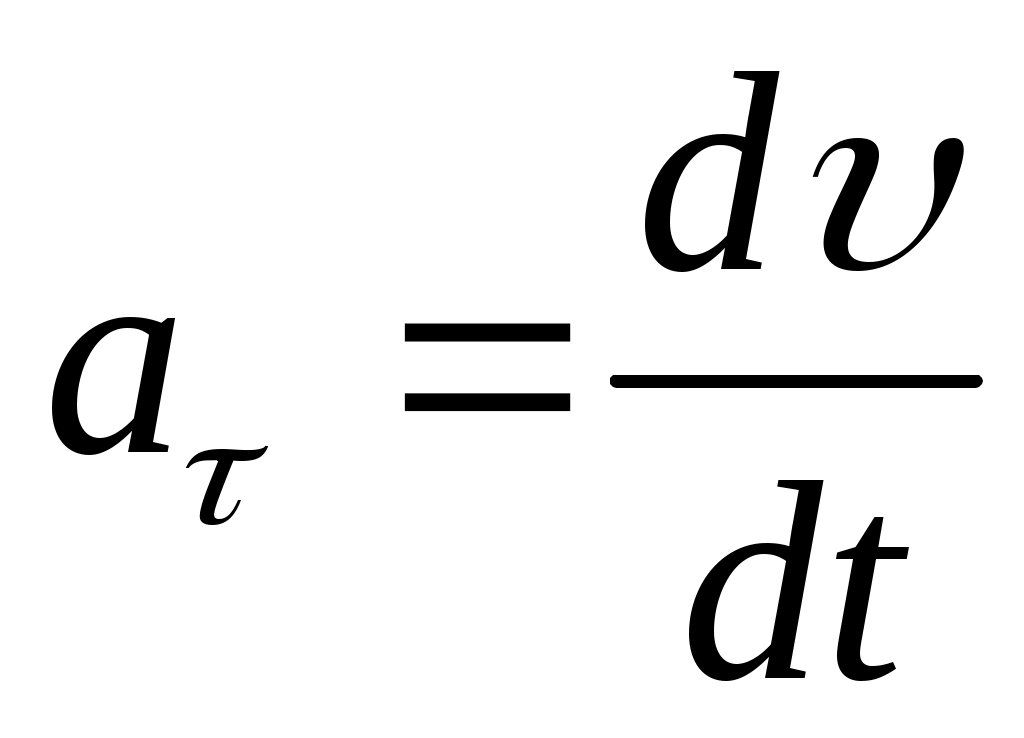 и и 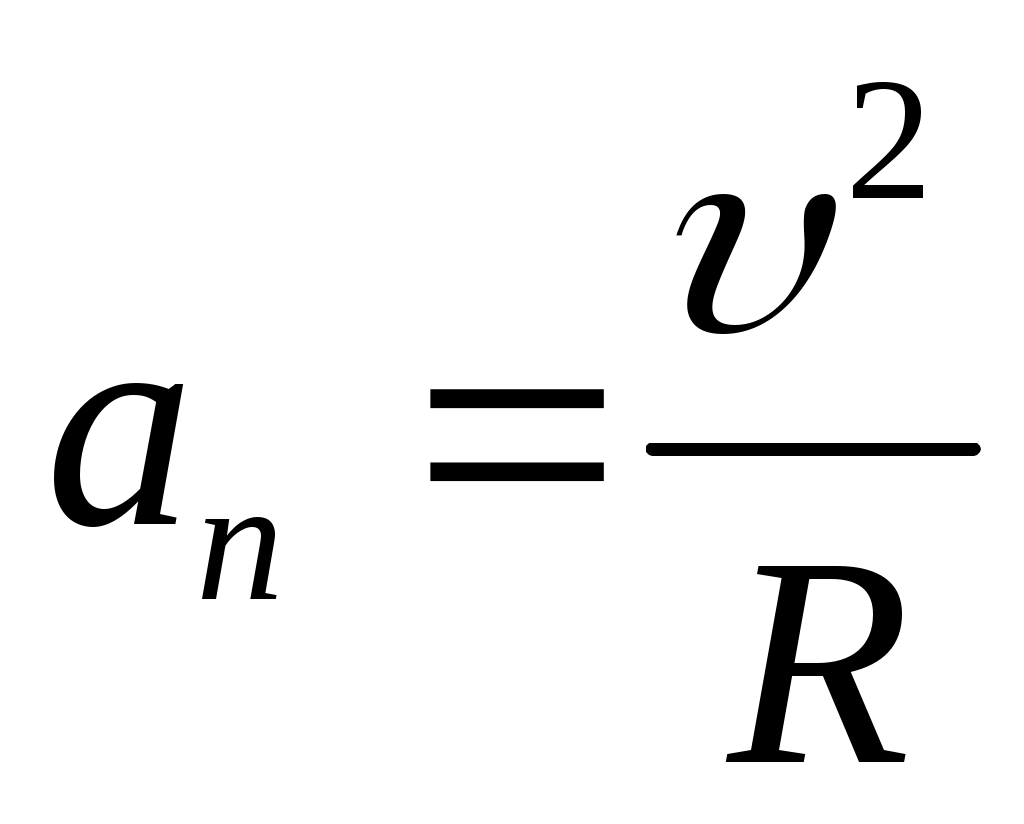 , а также , а также  можно записать: можно записать:
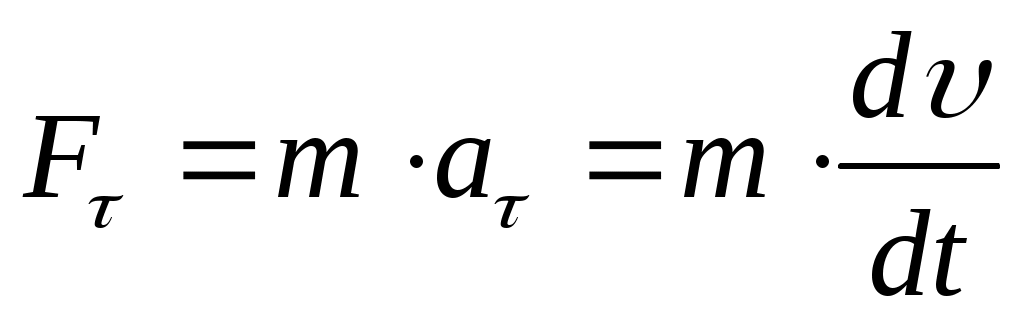 ; ;
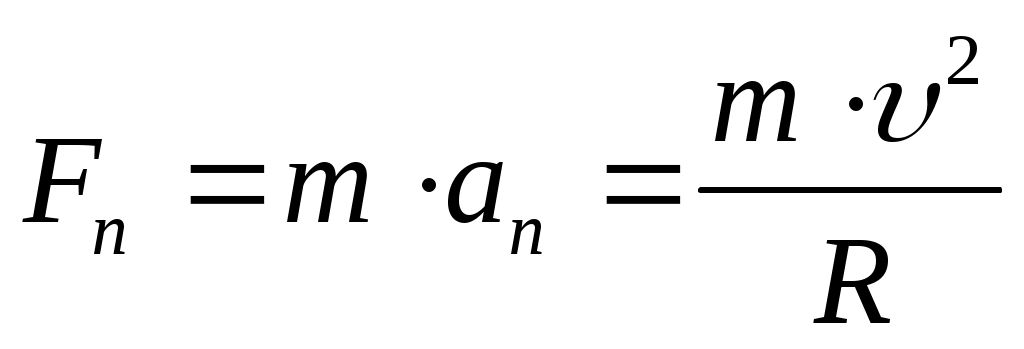 . .
Если на тело одновременно действуют несколько сил (например, 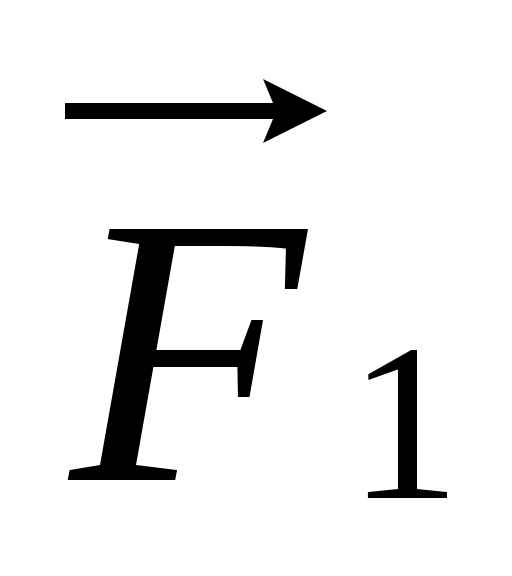  и и 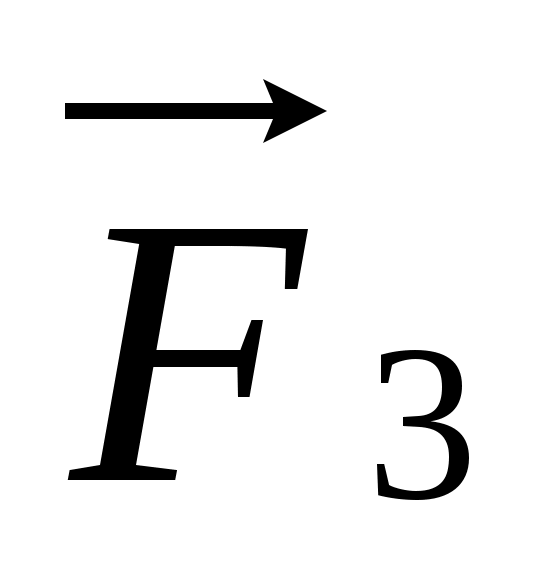 то под силой то под силой 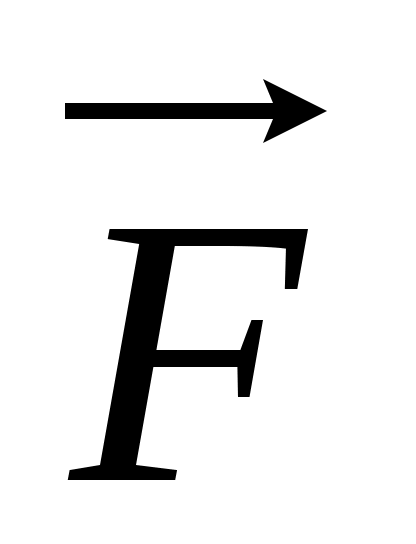 в формуле, выражающей второй закон Ньютона, нужно понимать равнодействующую всех сил: в формуле, выражающей второй закон Ньютона, нужно понимать равнодействующую всех сил:
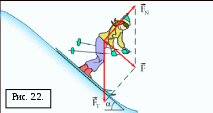
Сила 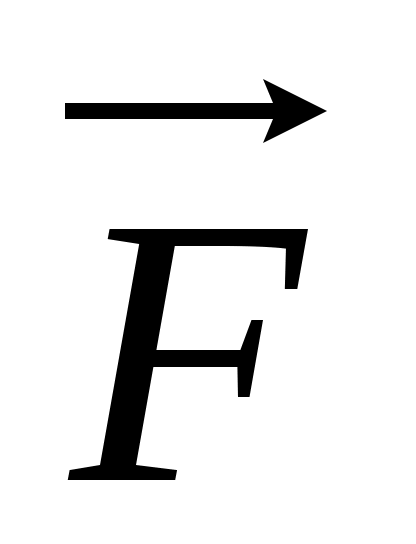 – равнодействующая силы тяжести – равнодействующая силы тяжести 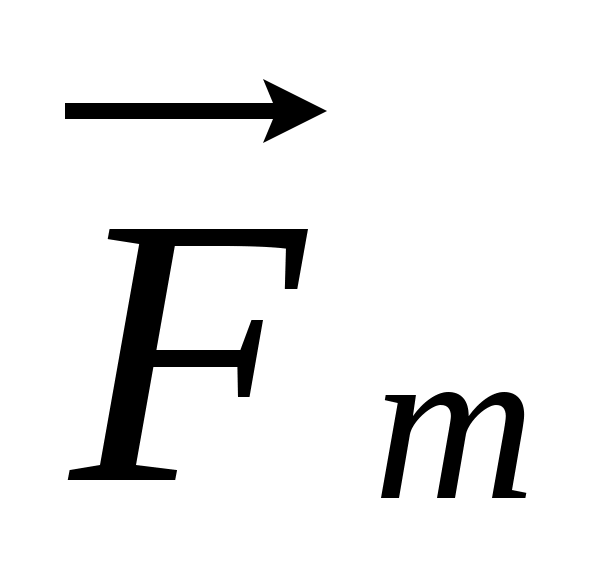 и силы нормального давления и силы нормального давления 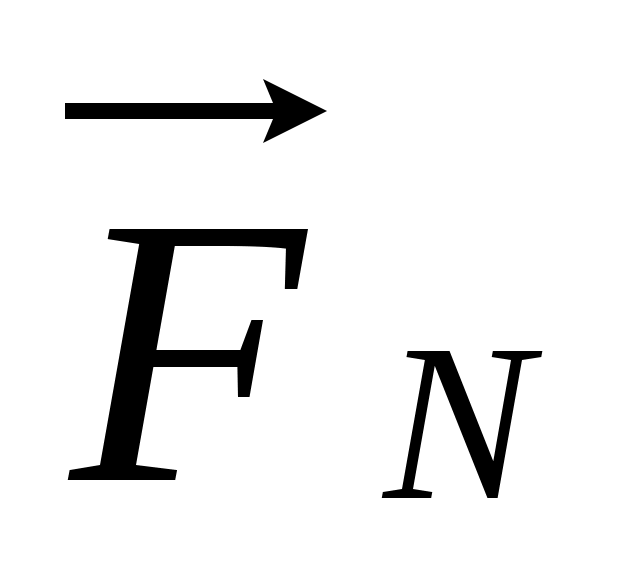 действующих на лыжницу на гладкой горе. Сила действующих на лыжницу на гладкой горе. Сила 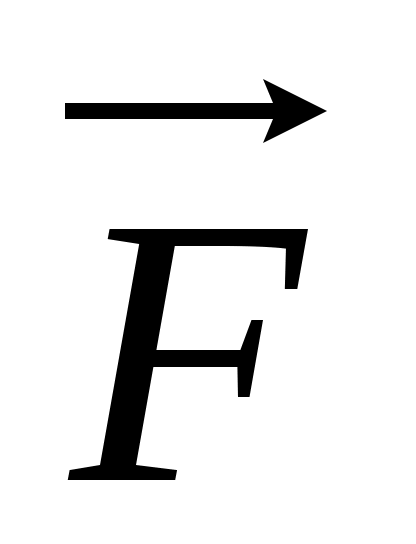 вызывает ускорение лыжника. вызывает ускорение лыжника.
§ 3. Третий закон Ньютона
Третий законом Ньютона: силы, с которыми действуют друг на друга материальные точки, всегда равны по модулю, противоположно направлены и действуют вдоль прямой, соединяющей эти точки:
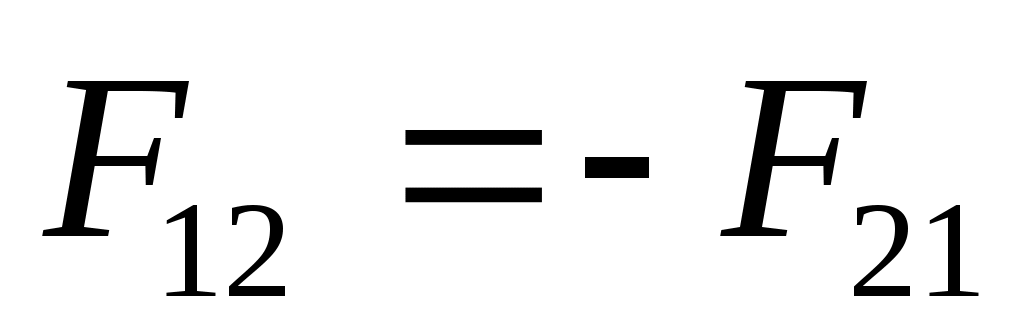 (3.1) (3.1)
где F12 — сила, действующая на первую материальную точку со стороны второй; F21 — сила, действующая на вторую материальную точку со стороны первой.
Рис. 3.1 иллюстрирует третий закон Ньютона. Человек действует на груз с такой же по модулю силой, с какой груз действует на человека. Эти силы направлены в противоположные стороны. Они имеют одну и ту же физическую природу – это упругие силы каната. Сообщаемые обоим телам ускорения обратно пропорциональны массам тел.
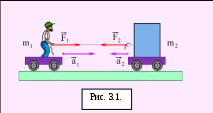
В этом случае: 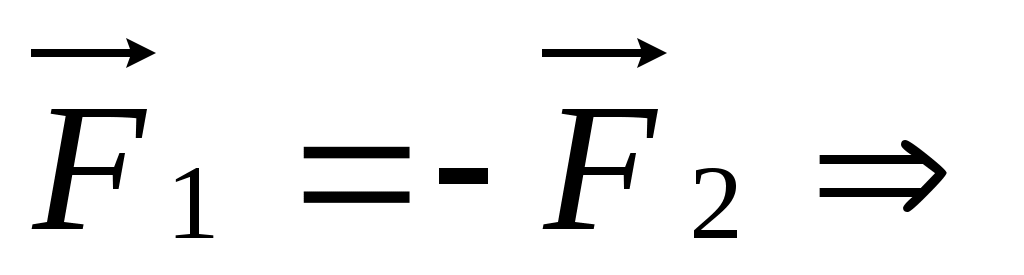 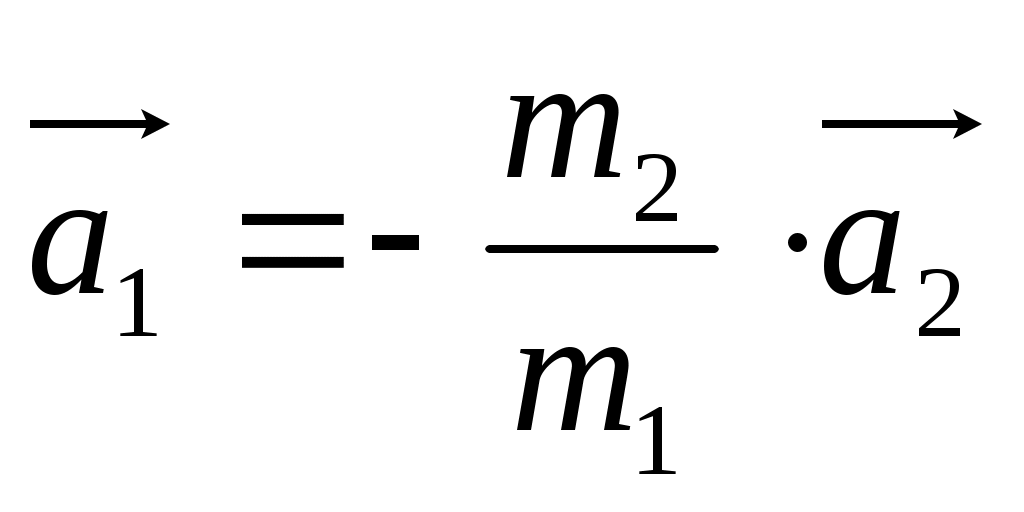 . .
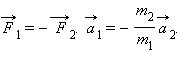
§ 4. Силы трения
Силы трения – силы, которые препятствует скольжению соприкасающихся тел друг относительно друга.
Силы трения зависят от относительных скоростей тел. В результате действия сил трения их механическая энергия всегда превращается во внутреннюю энергию соприкасающихся тел.
Различают внешнее (сухое) и внутреннее (жидкое или вязкое) трение. Внешним трением называется трение, возникающее в плоскости касания двух соприкасающихся тел при их относительном перемещении.
Силами сухого трения называют силы, возникающие при соприкосновении двух твердых тел при отсутствии между ними жидкой или газообразной прослойки. Они всегда направлены по касательной к соприкасающимся поверхностям.
Если соприкасающиеся тела неподвижны друг относительно друга, говорят о трении покоя, если же происходит относительное перемещение этих тел, то в зависимости от характера их относительного движения говорят о трениискольжения, качения или верчения. Сила трения покоя всегда равна по величине внешней силе и направлена в противоположную сторону (рис. 4.1.).
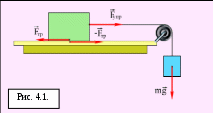
Сила трения покоя (υ = 0). 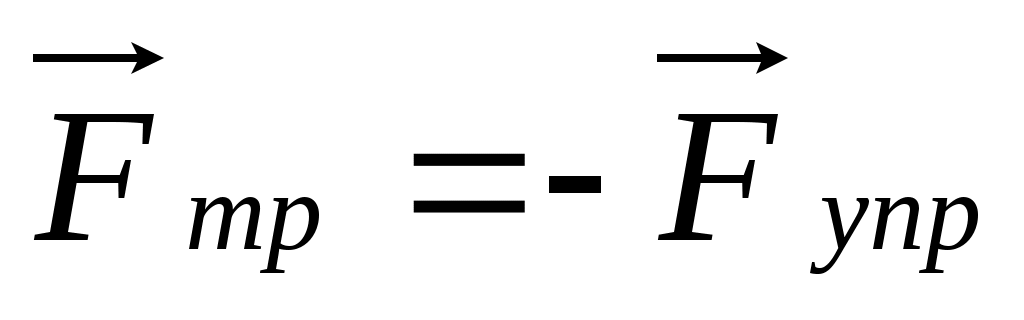
Внутренним трением называется трение между частями одного и того же тела, например между различными слоями жидкости или газа, скорости которых меняются от слоя к слою.
Рассмотрим лежащее на плоскости тело (рис. 4.2), к которому приложена горизонтальная сила F. Тело придёт в движение лишь тогда, когда приложенная сила F будет больше силы трения Fтр. Отсюда следует закон: сила трения Fтр пропорциональна силе N нормального действия, с которой одно тело действует на другое:
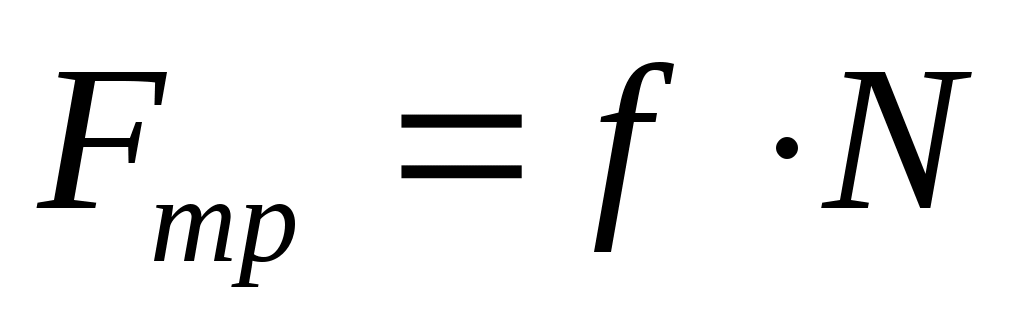
где f – коэффициент трения скольжения.
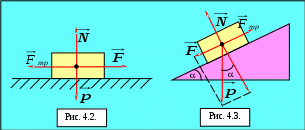
Если тело находится на наклонной плоскости с углом наклона , то оно приходит в движение, только когда тангенциальная составляющая F силы тяжести P больше силы трения Fтр. Следовательно:
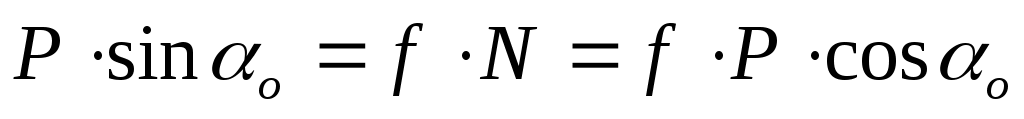 откуда откуда 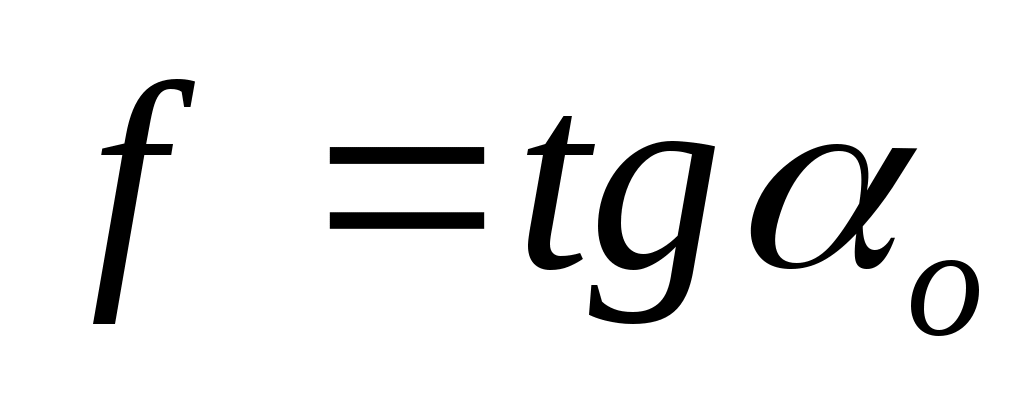
Таким образом, коэффициент трения равен тангенсу угла о, при котором начинается скольжение тела по наклонной плоскости.
Для гладких поверхностей определенную роль начинает играть межмолекулярное притяжение. Для них применяется закон трения скольжения
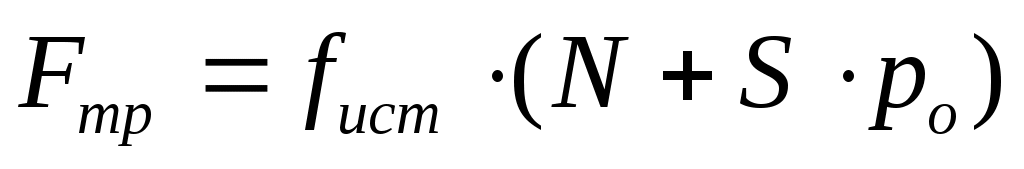
где po — добавочное давление, обусловленное силами межмолекулярного притяжения, которые быстро уменьшаются с увеличением расстояния между частицами; S— площадь контакта между телами; fист— истинный коэффициент трения скольжения.
В некоторых случаях силы трения оказывают вредное действие и поэтому их надо уменьшать. Для этого на трущиеся поверхности наносят смазку (сила трения уменьшается примерно в 10 раз), которая заполняет неровности между этими поверхностями и располагается тонким слоем между ними так, что поверхности как бы перестают касаться друг друга, а скользят друг относительно друга отдельные слои жидкости. Таким образом, внешнее трение твердых тел заменяется значительно меньшим внутренним трением жидкости.
Радикальным способом уменьшения силы трения является замена трения скольжения трением качения (шариковые н роликовые подмышники и т. д.). Сила трения качения определяется по закону, установленному Кулоном:
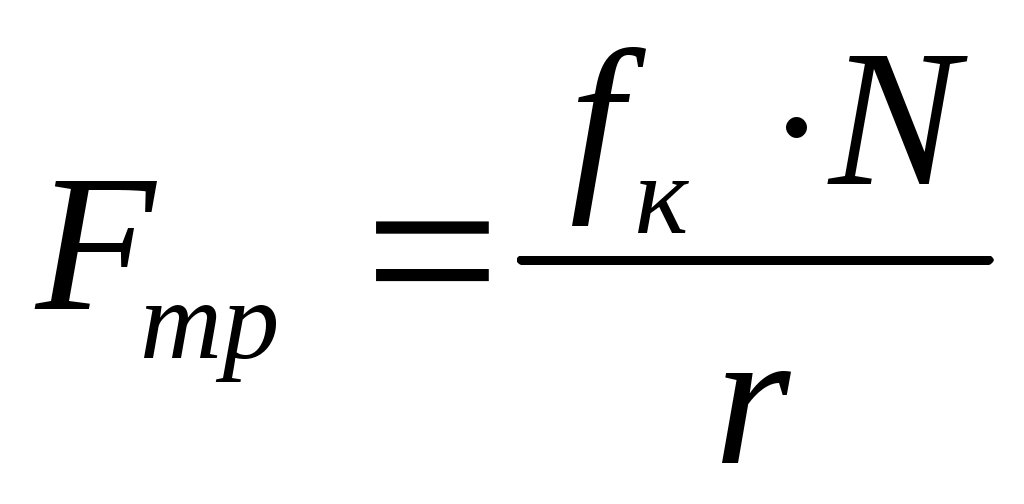 (4.1) (4.1)
где r — радиус катящегося тела; fк — коэффициент трения качения.
Из (4.1) следует, что сила трения качения обратно пропорциональна радиусу катящегося тела.
§ 5. Закон сохранения импульса
Силы взаимодействия между материальными точками механической системы называются внутренними. Силы, с которыми на материальные точки системы действуют внешние тела, называются внешними.
Рассмотрим механическую систему, состоящую из n тел, масса и скорость которых соответственно равны т1, т2... , тnи 1, 2 ..., n . Пусть F'1, F'2, ... , F'n — равнодействующие внутренних сил, действующих на каждое из этих тел, a, F1, F2 ..., Fn— равнодействующие внешних сил. Запишем второй закон Ньютона для каждого из n тел механической системы:
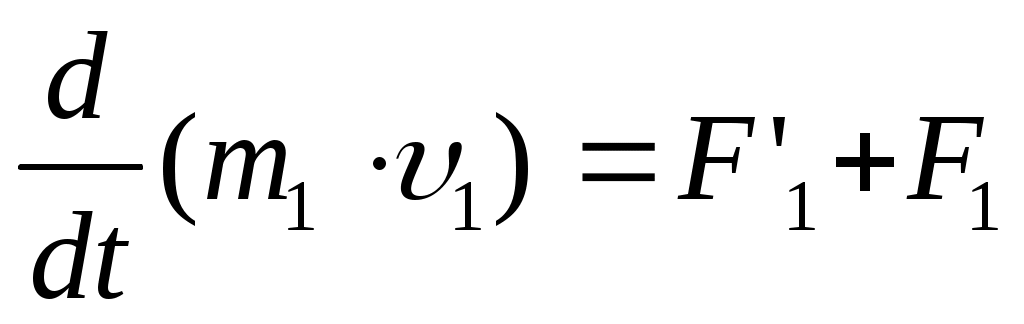 , , 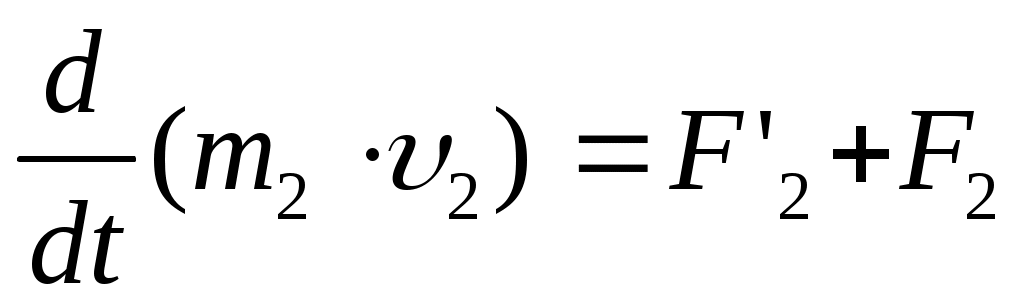 , ,
………………
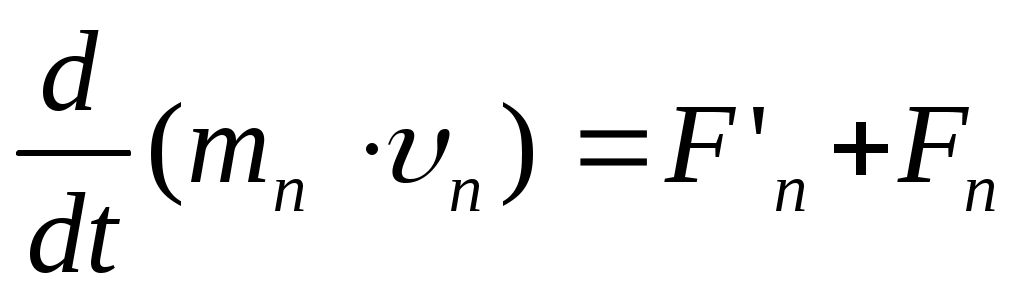 , ,
Складывая почленно эти уравнения, получаем:
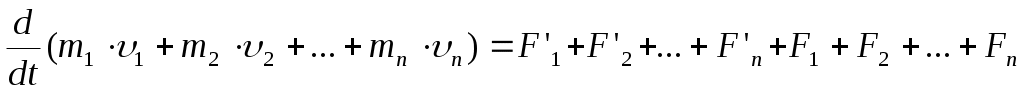
Но так как геометрическая сумма внутренних сил механической системы по третьему закону Ньютона равна нулю, то:
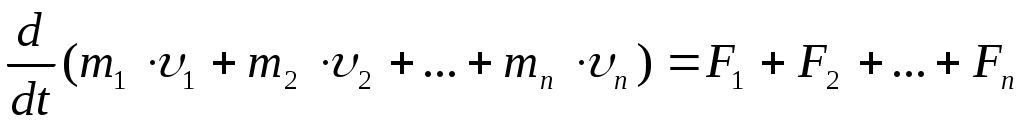 или или
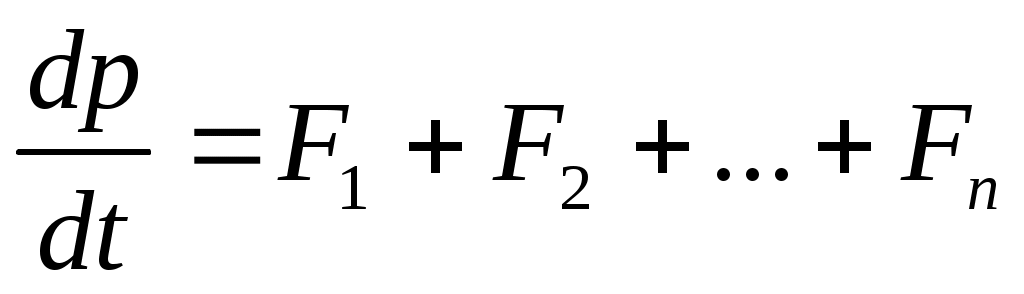 (5.1) (5.1)
где  — импульс системы. Таким образом, производная по времени от импульса механической системы равна геометрической сумме внешних сил, действующих на систему: — импульс системы. Таким образом, производная по времени от импульса механической системы равна геометрической сумме внешних сил, действующих на систему:
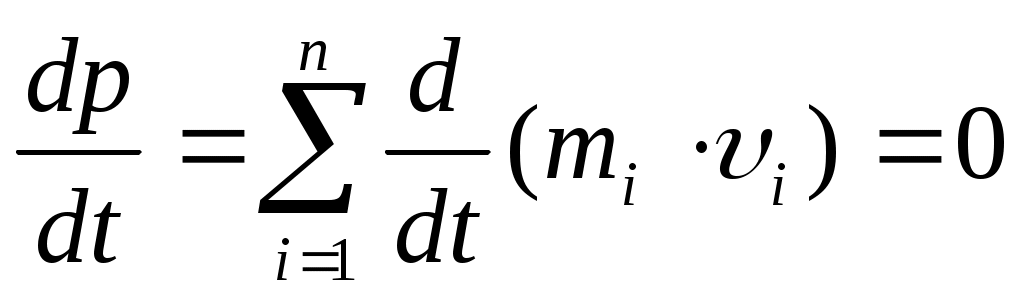 т.е. т.е. 
Последнее выражение и является законом сохранения импульса: импульс замкнутой системы сохраняется, т. е. не изменяется с течением времени.
КОНТРОЛЬНЫЕ ВОПРОСЫ:
Какая система отсчета называется инерциальной? Почему система отсчета, связанная с Землей, строго говоря, неинерциальная?
Что такое сила? Как ее можно охарактеризовать?
Является ли первый закон Ньютона следствием второго закона? Почему?
Какова физическая сущность трения? В чём отличие сухого трения от жидкого? Какие виды внешнего (сухого) трения Вы знаете?
Что называется механической системой? Какие системы являются замкнутыми? Является ли Вселенная замкнутой системой? Почему?
В чем заключается закон сохранения импульса? В каких системах он выполняется? Почему он является фундаментальным законом природы?
Каким свойством пространства обусловливается справедливость закона сохранения импульса?
Что называется центром масс системы материальных точек? Как движется центр масс замкнутой системы?
- -
|
 Скачать 249 Kb.
Скачать 249 Kb. то свойство масс называют аддитивностью.
то свойство масс называют аддитивностью.





