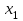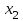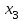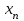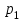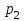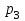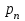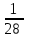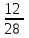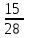ХТФ-Л2(часть1). Закон распределения и числовые характеристики
 Скачать 0.56 Mb. Скачать 0.56 Mb.
|
|
2. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ 2.1. ДИСКРЕТНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ. ЗАКОН РАСПРЕДЕЛЕНИЯ И ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ Для более глубокого изучения материала советуем изучить рекомендованные разделы учебной литературы (нумерация соответствует номерам литературы, указанной в библиографическом списке пособия). Литература: [3] гл.6 §2-3, гл.7 §1-2, гл.8 §3-4; [7] гл.2 п.2.1-2.2, 2.5; [8] гл. 2 §10, 12; [9]. Случайная величина – это величина, которая в результате опыта примет одно и только одно значение, неизвестное заранее. Если случайная величина принимает отдельные, изолированные значения, то ее называют дискретной; если же случайная величина принимает все значения из некоторого промежутка (конечного или бесконечного), то ее называют непрерывной. Примером дискретной случайной величины может служить число очков, выпадающих на верхней грани при бросании игральной кости (она может принимать изолированные значения: 1, 2, 3, 4, 5,6). Пример непрерывной случайной величины – время безотказной работы прибора (она принимает все значения из некоторого промежутка 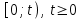 ). ).Закон распределения дискретной случайной величины – соответствие между ее возможными значениями и соответствующими вероятностями. Закон распределения может быть задан: таблично (рядом распределения) – с перечислением всех значений случайной величины и соответствующих им вероятностей
Отметим, что в этом случае сумма вероятностей равна единице, т.е. 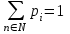 ; ; аналитически – с помощью формулы, в т.ч. с помощью интегральной функции распределения вероятностей (речь об этой функции пойдет ниже); графически – в виде графика интегральной функции распределения вероятностей или в виде многоугольника распределения. Если в прямоугольной системе координат Охр отметить точки 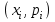 , где , где 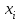 – возможные значения случайной величины Х, а – возможные значения случайной величины Х, а 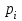 – соответствующие вероятности, и соединить эти точки отрезками прямых, то полученную ломаную называют многоугольником распределения. – соответствующие вероятности, и соединить эти точки отрезками прямых, то полученную ломаную называют многоугольником распределения.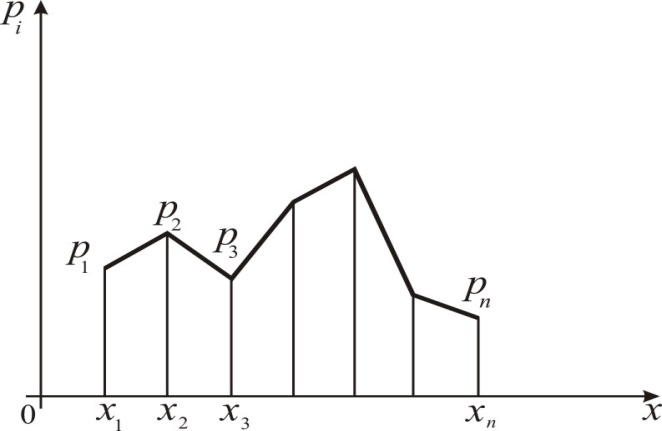 Рис.1 Закон распределения дискретной случайной величины полностью описывает ее с вероятностной точки зрения. Однако иногда он неизвестен, или не удобен для восприятия (например, в случае большого количества значений случайной величины). В таких случаях предпочитают использовать числовые параметры, описывающие случайную величину «суммарно» – числовые характеристики, которые в сжатой форме выражают наиболее существенные черты распределения. Чаще всего используют числовые характеристики положения (математическое ожидание, мода) и характеристики рассеяния (дисперсия, стандартное отклонение). Математическое ожидание дискретной случайной величины – это среднее значение случайной величины, взвешенное по вероятностям. Для дискретной случайной величины математическое ожидание равно сумме произведений всех ее возможных значений на их вероятности, т.е. если дан ряд распределения случайной величины, то 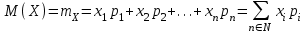 . (2.1) . (2.1)Свойства математического ожидания: 1)  ; ;2)  ; ;3) 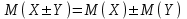 ; ;4) 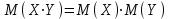 , если , если 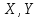 независимы; независимы;5) для биномиального распределения 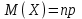 . .Дисперсия (рассеяние) дискретной случайной величины – это математическое ожидание квадрата отклонения случайной величины от ее математического ожидания, т.е. 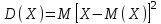 . (2.2) . (2.2)На практике часто используют следующую формулу 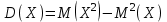 , где , где 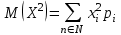 . (2.3) . (2.3)Свойства дисперсии: 1) 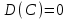 ; ;2) 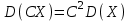 ; ;3) 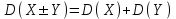 ; ;4) 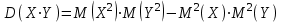 , если , если 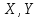 независимы; независимы;5) для биномиального распределения 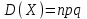 . .Дисперсия имеет размерность квадрата случайной величины, что в сравнительных целях не всегда удобно. Поэтому, когда хотят, чтобы оценка рассеяния имела размерность случайной величины, рассматривают еще одну числовую характеристику – стандартное отклонение. Среднее квадратическое отклонение (стандартное отклонение) дискретной случайной величины есть квадратный корень из дисперсии, т.е. 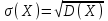 . (2.4) . (2.4)Мода 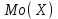 дискретной случайной величины – значение случайной величины, принимаемое с наибольшей вероятностью по сравнению с двумя соседними значениями. дискретной случайной величины – значение случайной величины, принимаемое с наибольшей вероятностью по сравнению с двумя соседними значениями.Функция распределения (интегральная функция распределения) случайной величины – функция, определяющая для каждого значения аргумента вероятность того, что случайная величина примет значение меньше, чем значение этого аргумента, т.е. 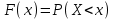 . .Свойства функции распределения: 1) 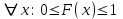 ; ;2) 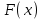 – неубывающая функция; – неубывающая функция;3) 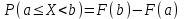 ; ;4) 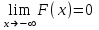 , , 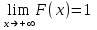 ; ;5) 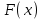 непрерывна слева. непрерывна слева.Отметим, что график функции распределения дискретной случайной величины имеет ступенчатый вид и претерпевает разрыв в каждой точке 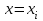 , где , где 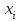 – значения, принимаемые случайной величиной. – значения, принимаемые случайной величиной.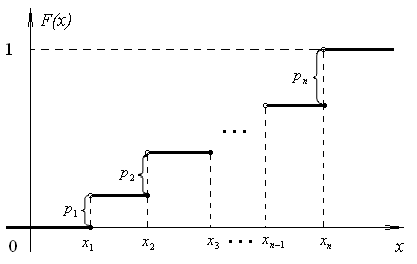 Рис. 2 Для непрерывной случайной величины функция распределения непрерывна и дифференцируема всюду, за исключением, быть может, конечного числа точек. Пример 1. В партии из 8 деталей 2 бракованных. Наудачу взяли 2 детали. Составьте ряд распределения случайной величины – числа стандартных деталей в выборке. Найдите числовые характеристики этой случайной величины. Решение. Дискретная случайная величина  – число стандартных деталей из двух взятых. Она может принимать значения: 0, 1, или 2. Чтобы составить ее ряд распределения, найдем соответствующие вероятности, рассматривая каждое значение случайной величины как отдельное случайное событие: – число стандартных деталей из двух взятых. Она может принимать значения: 0, 1, или 2. Чтобы составить ее ряд распределения, найдем соответствующие вероятности, рассматривая каждое значение случайной величины как отдельное случайное событие:событие 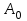 – взяли два бракованных изделия, – взяли два бракованных изделия,  ; ;событие 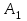 – взяли только одно стандартное изделие, – взяли только одно стандартное изделие, 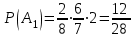 ; ;событие 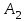 – взяли два стандартных изделия, – взяли два стандартных изделия, 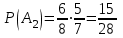 . .Отметим, что в данном случае для нахождения вероятностей была использована теорема о вероятности произведения зависимых событий. Тот же результат может быть получен с помощью формулы классической вероятности. Итак, ряд распределения числа стандартных деталей в выборке имеет вид:
Заметим, что сумма полученных вероятностей 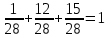 , так как рассмотренные нами события , так как рассмотренные нами события 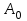 , , 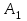 , , 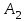 образуют полную группу. образуют полную группу.Вычислим числовые характеристики этой случайной величины: 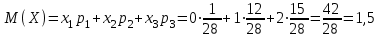 ; ;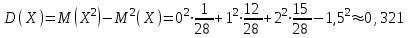 ; ;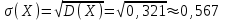 ; ;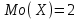 (т.к. значению (т.к. значению 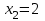 соответствует самая большая вероятность). соответствует самая большая вероятность).Пример 2. Производят три независимых выстрела, вероятность попадания в каждом из которых равна 0,4. Рассматривается дискретная случайная величина 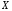 – число попаданий в мишень в трех опытах. Постройте ряд распределения и найдите числовые характеристики этой случайной величины. Составьте функцию распределения случайной величины – число попаданий в мишень в трех опытах. Постройте ряд распределения и найдите числовые характеристики этой случайной величины. Составьте функцию распределения случайной величины 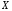 и постройте ее график. и постройте ее график.Решение. Дискретная случайная величина 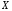 – число попаданий в мишень при трех выстрелах. Возможные значения этой случайной величины – 0, 1, 2, 3. Чтобы составить закон распределения этой величины, найдем соответствующие вероятности с помощью формулы Бернулли: – число попаданий в мишень при трех выстрелах. Возможные значения этой случайной величины – 0, 1, 2, 3. Чтобы составить закон распределения этой величины, найдем соответствующие вероятности с помощью формулы Бернулли:число испытаний 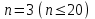 ; ;событие 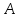 – попадание в мишень при одном выстреле; – попадание в мишень при одном выстреле; 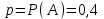 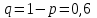 . .По формуле Бернулли вычисляем: 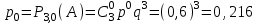 ; ; 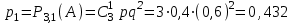 ; ;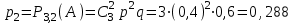 ; ; 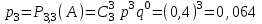 . .Таким образом, ряд распределения случайной величины 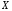 имеет вид: имеет вид:
(Контроль: 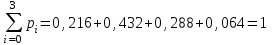 ). ).Числовые характеристики этой случайной величины можно вычислить с помощью формул (как это было сделано в предыдущем примере). Например, 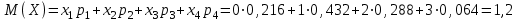 . . Однако в данном случае гораздо проще воспользоваться свойствами для математического ожидания и дисперсии №5, поскольку данное распределение является биномиальным (так как оно определялось формулой Бернулли). Получим: 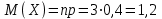 ; ;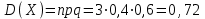 ; ;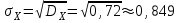 ; ;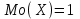 . .Заметим, что для нахождения числовых характеристик биномиальной случайной величины НЕ требуется составления ряда распределения. Составим интегральную функцию, используя ее определение: 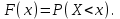 Будем находить значения интегральной функции отдельно на каждом промежутке, на которые разбивают числовую прямую значения данной случайной величины. 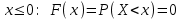 (т.к. событие (т.к. событие 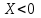 – событие невозможное); – событие невозможное);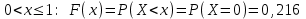 ; ;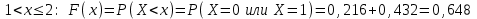 ; ;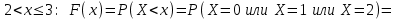 = 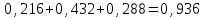 ; ;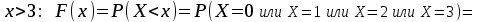 = 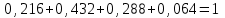 . .Итак, интегральная функция имеет вид 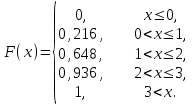 Обратим внимание читателя на соответствие полученного результата свойствам функций распределения: ее значения принадлежат отрезку [0, 1], при 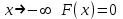 ; а при ; а при 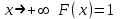 . .Построим график интегральной функции распределения. Как и было указано в свойствах интегральной функции, он имеет ступенчатый вид с разрывами в точках 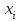 = 0, 1, 2, 3. = 0, 1, 2, 3.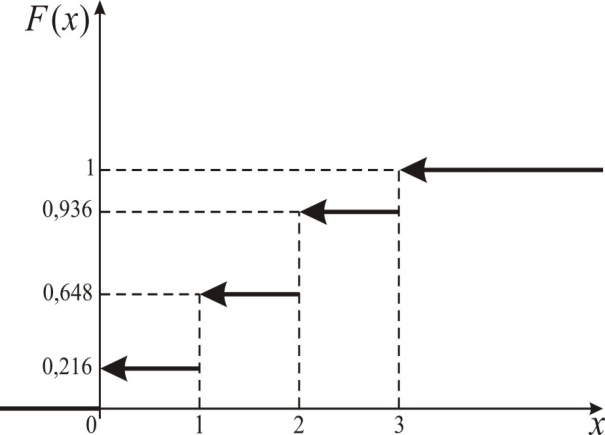 Полученный график функции распределения можно рассматривать как еще один способ задания закона распределения случайной величины – графический. 2.2. НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ. ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ И ПЛОТНОСТЬ ВЕРОЯТНОСТИ, ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ Для более глубокого изучения материала советуем изучить рекомендованные разделы учебной литературы (нумерация соответствует номерам литературы, указанной в библиографическом списке пособия). Литература: [3] гл.10 §1-2, гл.11 §1-3; [7] гл.2 п.2.3-2.5; [8] гл. 2 §11, 13. Напомним, что случайная величина называется непрерывной, если все ее значения непрерывно заполняют некоторый промежуток (конечный или бесконечный). Поскольку число значений непрерывной случайной величины всегда бесконечно, ясно, что составить ряд распределения не представляется возможным. Непрерывная случайная величина может быть задана функцией распределения или дифференциальной функцией распределения. Отметим, что если случайная величина непрерывна, то ее интегральная функция распределения непрерывна и дифференцируема всюду, кроме, быть может, отдельных точек (а так же удовлетворяет всем свойствам, перечисленным в п. 2.1). Дифференциальная функция распределения (плотность распределения вероятностей) непрерывной случайной величины – производная ее функции распределения, т.е. 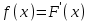 . .График дифференциальной функции распределения называют кривой распределения. Свойства плотности распределения: 1) 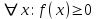 ; ;2) 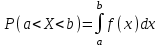 ; ;3) 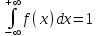 ; ;4) 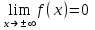 ; ;5) 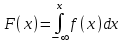 . .Математическое ожидание непрерывной случайной величины – это среднее значение случайной величины, взвешенное по вероятностям. Для непрерывной случайной величины математическое ожидание есть число, определяемое равенством 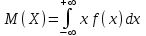 . (2.5) . (2.5)В частности, если все значения случайной величины принадлежат отрезку 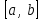 , то математическое ожидание определяют равенством , то математическое ожидание определяют равенством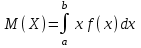 . (2.6) . (2.6)Дисперсия (рассеяние) непрерывной случайной величины – математическое ожидание квадрата отклонения случайной величины от ее математического ожидания, т.е. 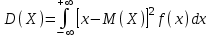 . (2.7) . (2.7)В частности, если все значения случайной величины принадлежат отрезку 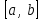 , то ее дисперсию определяют равенством , то ее дисперсию определяют равенством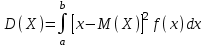 . (2.8) . (2.8)На практике часто используют более удобные формулы 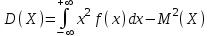 , (2.9) , (2.9)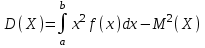 . (2.10) . (2.10)Свойства математического ожидания и дисперсии, указанные для дискретных случайных величин, сохраняются и для непрерывных величин. Среднее квадратическое отклонение непрерывной случайной величины – квадратный корень из дисперсии, т.е. 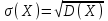 . (2.11) . (2.11)Мода 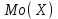 непрерывной случайной величины – точка локального максимума плотности вероятности непрерывной случайной величины – точка локального максимума плотности вероятности 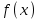 . .Медиана 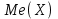 непрерывной случайной величины – такое ее значение, для которого непрерывной случайной величины – такое ее значение, для которого 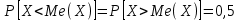 . (2.12) . (2.12)Геометрически медиану можно истолковать как точку, в которой ордината 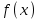 делит пополам площадь под кривой распределения. делит пополам площадь под кривой распределения.Пример 1. Непрерывная случайная величина 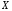 задана функцией распределения задана функцией распределения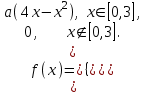 . .Найдите параметр  и числовые характеристики этой случайной величины. и числовые характеристики этой случайной величины.Решение. Неизвестный параметр найдем, используя свойство №3 плотности распределения (свойство нормировки): 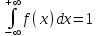 . .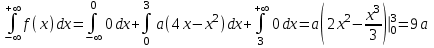 ; ; 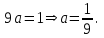 Так, плотность распределения данной случайной величины имеет вид 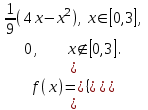 Найдем ее числовые характеристики. Поскольку все значения данной случайной величины принадлежат отрезку 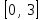 , то по формуле (2.6) получим: , то по формуле (2.6) получим: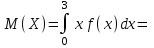 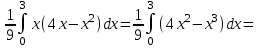 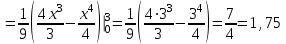 . .Дисперсию вычислим по формуле (2.10): 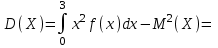 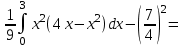 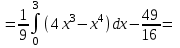 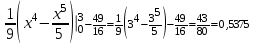 ; ;тогда 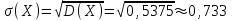 . .Мода случайной величины – точка локального максимума ее дифференциальной функции. Поскольку плотность вероятностей есть квадратичная функция, графиком которой является парабола (ветви направлены вниз), то легко определить точку ее максимума – это ее вершина. Находим по формуле 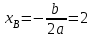 . Таким образом, . Таким образом, 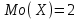 . .Пример 2. Непрерывная случайная величина 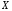 задана функцией плотности распределения задана функцией плотности распределения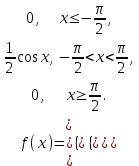 Найдите интегральную функцию этой случайной величины. Вычислите вероятность того, что значение случайной величины попадет в интервал 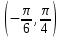 и покажите эту вероятность на графике. и покажите эту вероятность на графике.Решение. Интегральную функцию найдем, используя свойство №5 дифференциальной функции распределения: 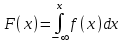 . . Заметим, что плотность вероятности задана кусочно (что встречается довольно часто). Поэтому значения интегральной функции будем находить отдельно на каждом из промежутков, на которых задана дифференциальная функция. Получаем: 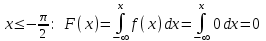 ; ;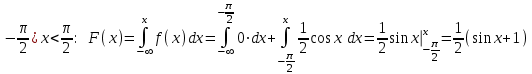 ; ;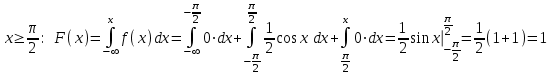 . .Таким образом, интегральная функция распределения данной случайной величины имеет вид 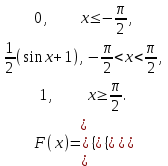 Вероятность попадания данной случайной величины в интервал 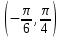 можно найти двумя способами. С помощью интегральной функции распределения (свойство №3, п. 2.1): можно найти двумя способами. С помощью интегральной функции распределения (свойство №3, п. 2.1):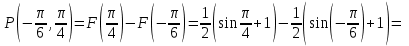 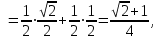 или с помощью дифференциальной функции распределения (свойство №2, п.2.2): 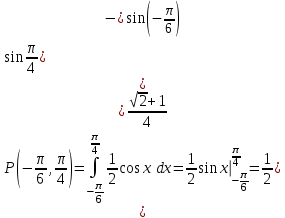 . .Второй способ вычисления дает возможность геометрической интерпретации полученного результата, поскольку известно, что геометрический смысл определенного интеграла – есть площадь фигуры. Вероятность попадания случайной величины в интервал 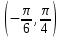 графически можно интерпретировать как площадь под кривой распределения, ограниченной слева прямой графически можно интерпретировать как площадь под кривой распределения, ограниченной слева прямой 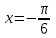 и справа – прямой и справа – прямой 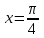 . Построим график кривой распределения и покажем искомую вероятность. . Построим график кривой распределения и покажем искомую вероятность.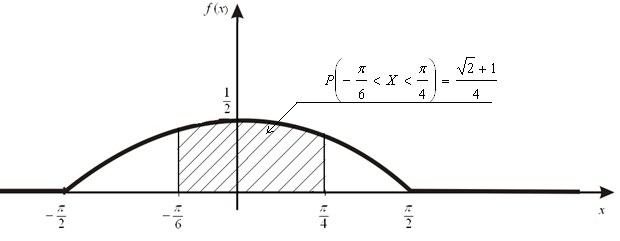 2.3. НЕКОТОРЫЕ ТИПИЧНЫЕ ЗАКОНЫ РАСПРЕДЕЛЕНИЯ НЕПРЕРЫВНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН Для более глубокого изучения материала советуем изучить рекомендованные разделы учебной литературы (нумерация соответствует номерам литературы, указанной в библиографическом списке пособия). Литература: [3] гл.12 §1-3, гл.13 §1-3; [7] гл.2 п.2.7. 2.3.1. РАВНОМЕРНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ Непрерывная случайная величина называется равномерно распределенной на интервале 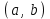 , если ее плотность вероятностей постоянна на этом интервале, а вне его равна нулю, т.е. , если ее плотность вероятностей постоянна на этом интервале, а вне его равна нулю, т.е.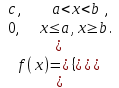 Значение константы 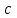 легко определить с помощью свойства нормировки непрерывной случайной величины (см. п. 2.1): легко определить с помощью свойства нормировки непрерывной случайной величины (см. п. 2.1): 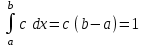 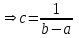 . .Тогда равномерная случайная величина имеет плотность распределения: 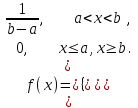 Обозначают: 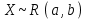 . .Кривая распределения равномерной случайной величины имеет вид:  Рис. 4 Интегральная функция распределения равномерной случайной величины: 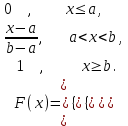 График интегральной функции распределения имеет вид:  Рис. 5 Числовые характеристики равномерного распределения легко вычислить так, как это было сделано ранее (см. п. 2.2). Получим следующие формулы: 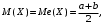 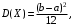 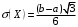 . .Вероятность попадания равномерной случайной величины в интервал 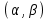 , принадлежащий целиком интервалу , принадлежащий целиком интервалу 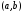 , можно вычислить по формуле , можно вычислить по формуле 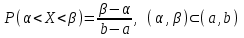 . (2.13) . (2.13)Геометрически эта вероятность представляет собой площадь прямоугольника, заштрихованного на графике функции 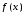 (см. рис. 4). Этот факт дает возможность вычислять вероятность попадания равномерной случайной величины в заданный промежуток из геометрических соображений – наиболее удобный в данном случае. (см. рис. 4). Этот факт дает возможность вычислять вероятность попадания равномерной случайной величины в заданный промежуток из геометрических соображений – наиболее удобный в данном случае.К равномерным величинам относятся те случайные величины, про которые известно, что все их значения лежат внутри некоторого промежутка, и все они имеют одинаковую вероятность. Среди них – время ожидания пассажирами транспорта, курсирующего с определенным интервалом, ошибка округления чисел до целых и пр. Замечание. Дискретную случайную величину называют равномерно распределенной, если она принимает целочисленные значения 1, 2, 3,…, 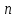 с равными вероятностями с равными вероятностями 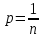 . .В этом случае 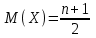 ; ; 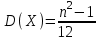 . .Примером равномерной дискретной величины может служить 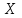 – число очков, выпавших на верхней грани игральной кости. Она может принять значения 1, 2, 3, 4, 5, 6 с равными вероятностями – число очков, выпавших на верхней грани игральной кости. Она может принять значения 1, 2, 3, 4, 5, 6 с равными вероятностями 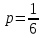 . .Ее числовые характеристики: 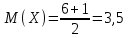 ; ; 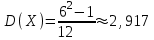 . .Пример.Случайная величина 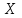 имеет равномерное распределение в интервале (1, 3). Напишите дифференциальную и интегральную функции, постройте их графики. Вычислите числовые характеристики и вероятность попадания случайной величины в интервал имеет равномерное распределение в интервале (1, 3). Напишите дифференциальную и интегральную функции, постройте их графики. Вычислите числовые характеристики и вероятность попадания случайной величины в интервал 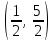 , покажите эту вероятность на графике. , покажите эту вероятность на графике.Решение. Случайная величина 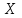 распределена по равномерному закону, следовательно, ее дифференциальная функция имеет вид: распределена по равномерному закону, следовательно, ее дифференциальная функция имеет вид: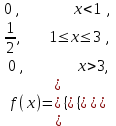 ее график: 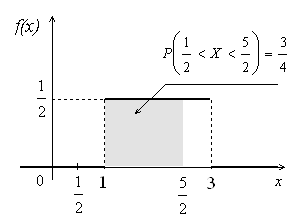 Интегральная функция имеет вид: 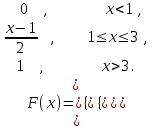 ее график: 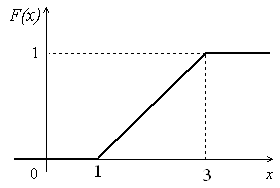 Вычислим числовые характеристики случайной величины: 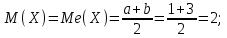 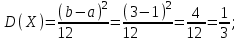 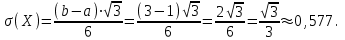 Вероятность попадания случайной величины в интервал 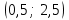 можно вычислить рассмотренными выше способами. Например, с помощью интегральной функции распределения: можно вычислить рассмотренными выше способами. Например, с помощью интегральной функции распределения: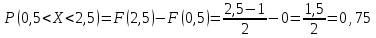 . .Можно воспользоваться формулой нахождения вероятности попадания равномерной величины в данный интервал (2.13) или найти вероятность из геометрических соображений. Последний вариант в данном случае кажется наиболее удобным. На графике дифференциальной функции заштрихуем площадь под кривой распределения на интервале 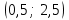 – получим прямоугольник, площадь которого численно равна искомой вероятности. Таким образом, – получим прямоугольник, площадь которого численно равна искомой вероятности. Таким образом, 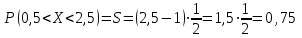 . .2.3.2. ПОКАЗАТЕЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ Непрерывная случайная величина называется распределенной по показательному (экспоненциальному) закону, если ее плотность вероятностей имеет вид 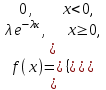 где число 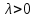 называется параметром распределения. называется параметром распределения.Кривая распределения равномерной случайной величины имеет вид: 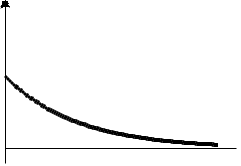 Рис. 6 Интегральная функция распределения показательной случайной величины: 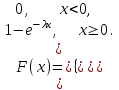 График интегральной функции распределения имеет вид: 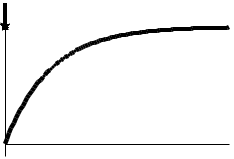 Рис. 7 Числовые характеристики показательного распределения: 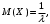 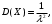 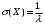 . .Вероятность попадания показательной случайной величины в интервал 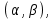 где где 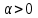 можно вычислить по формуле можно вычислить по формуле 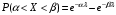 , , 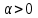 . (2.14) . (2.14)Пример.Случайная величина 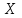 имеет показательное распределение с параметром имеет показательное распределение с параметром 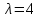 . Запишите дифференциальную и интегральную функции распределения этой случайной величины, постройте их графики. Найдите числовые характеристики случайной величины, а также вероятность попадания ее в интервал (1,5; 2,5), покажите эту вероятность на графике. . Запишите дифференциальную и интегральную функции распределения этой случайной величины, постройте их графики. Найдите числовые характеристики случайной величины, а также вероятность попадания ее в интервал (1,5; 2,5), покажите эту вероятность на графике.Решение. Случайная величина 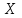 имеет показательное распределение с параметром имеет показательное распределение с параметром 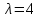 , следовательно, дифференциальная функция имеет вид: , следовательно, дифференциальная функция имеет вид: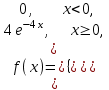 ее график: 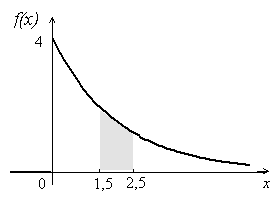 Интегральная функция имеет вид 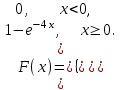 ее график: 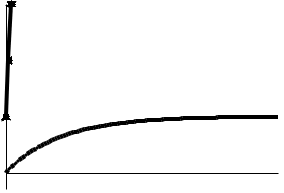 Числовые характеристики найдем по формулам: 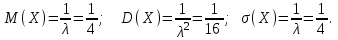 Вероятность попадания случайной величины в интервал (1,5; 2,5) найдем по формуле (2.14): 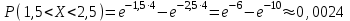 . .2.3.3. НОРМАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ Непрерывная случайная величина называется распределенной по нормальному закону, если ее плотность вероятностей имеет вид 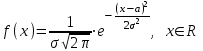 , ,где числа 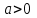 , , 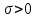 – параметры распределения. – параметры распределения.Обозначают: 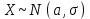 . .График плотности распределения вероятности нормального закона – кривая, которую называют нормальной кривой или кривой Гаусса. 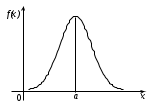 Рис. 8 Нормальное распределение с параметрами 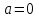 и и 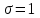 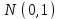 называют стандартным (нормированным). Плотность вероятности стандартной случайной величины имеет вид называют стандартным (нормированным). Плотность вероятности стандартной случайной величины имеет вид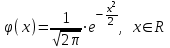 . .Напомним, что с этой функцией мы уже встречались выше (п. 1.4) – это функция Гаусса. Она четная и табулируемая – ее значения приведены в таблице (см. приложение 1), где для значений  следует считать следует считать  . .Интегральная функция распределения нормального распределения: 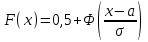 , ,где 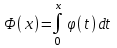 – функция Лапласа также уже была описана в п.1.4. Эта функция нечетная и табулируемая – ее значения приведены в таблице (см. приложение 2), где для значений – функция Лапласа также уже была описана в п.1.4. Эта функция нечетная и табулируемая – ее значения приведены в таблице (см. приложение 2), где для значений 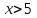 полагают полагают 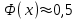 . .График интегральной функции нормального распределения имеет вид: 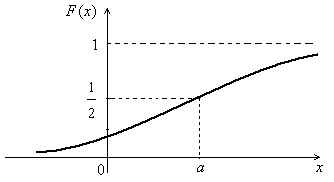 Рис. 9 При нахождении числовых характеристик нормального распределения становится ясен вероятностный смысл параметров распределения, так как: 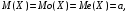 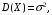 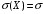 . .Вероятность попадания нормально распределенной случайной величины в интервал 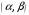 можно вычислить по формуле можно вычислить по формуле 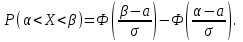 (2.15) (2.15)Вероятность отклонения нормально распределенной случайной величины от ее математического ожидания можно вычислить по формуле 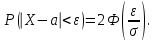 (2.16) (2.16)Последняя формула при подстановке в нее 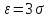 позволяет сделать важный вывод – правило трех сигма: практически достоверно (с вероятностью 0,9973), что абсолютное отклонение нормально распределенной случайной величины от ее математического ожидания не превосходит утроенного среднего квадратического отклонения, т.е. все ее значения лежат в промежутке позволяет сделать важный вывод – правило трех сигма: практически достоверно (с вероятностью 0,9973), что абсолютное отклонение нормально распределенной случайной величины от ее математического ожидания не превосходит утроенного среднего квадратического отклонения, т.е. все ее значения лежат в промежутке 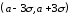 . .Закон Гаусса играет исключительную роль в теории вероятностей и математической статистике. Его отличительной особенностью является тот факт, что он является предельным законом, к которому (при определенных условиях) приближаются другие законы распределения. Именно нормальный закон распределения встречается на практике чаще других – им описывается большинство случайных явлений, связанных с производственными процессами; погрешности измерений в физических приборах, численность популяций некоторых видов животных, рост человека и мн. др. Пример 1. Средний процент выполнения плана некоторым предприятием составляет 105% со средним отклонением – 5%. Полагая, что выполнение плана предприятием подчинено закону нормального распределения, вычислить долю предприятий, выполняющих план от 110% до 130%. Решение. Случайная величина 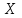 – процент выполнения плана предприятиями, она имеет нормальное распределение с параметрами – процент выполнения плана предприятиями, она имеет нормальное распределение с параметрами 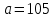 и и 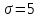 . Для нахождения искомой вероятности воспользуемся формулой (2.15): . Для нахождения искомой вероятности воспользуемся формулой (2.15):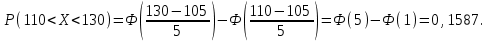 Так, доля предприятий, выполняющих план на 110% – 130%, составляет около 16% от общего числа предприятий. Пример 2. Длина изготовляемой детали представляет собой случайную величину, распределенную по нормальному закону. Средняя длина детали равна 50мм, а дисперсия – 0,25 мм2. Какое поле допуска длины изготовляемой детали можно гарантировать с вероятностью 0,99? Решение. Длина изготовляемой детали – случайная величина 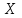 , имеющая нормальный закон распределения с параметрами , имеющая нормальный закон распределения с параметрами 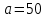 и и 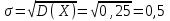 . Известна вероятность, гарантирующая поле допуска: . Известна вероятность, гарантирующая поле допуска: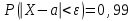 . .Воспользуемся указанной выше формулой (2.16) для нахождения отклонения 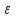 значений случайной величины от ее математического ожидания: значений случайной величины от ее математического ожидания: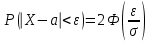 ; ;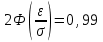 ; ;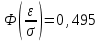 . .По таблице значений функции Лапласа (см. приложение 2) находим значение аргумента, при котором значение функции 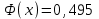 : :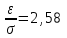 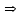 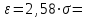 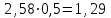 . .Тогда с вероятностью 0,99 можно указать поле допуска длины детали: 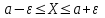 ; ;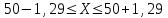 ; ;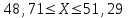 . . |