Ответы по Электромагнитным полям и волнам. Закон сохранения заряда
 Скачать 158.01 Kb. Скачать 158.01 Kb.
|
|
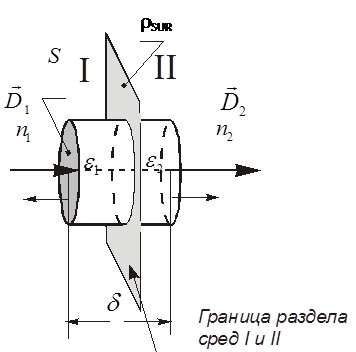
Врос 7. Третье и четвертое уравнения Максвелла и их физический смысл. Уравнения непрерывности и закон сохранения заряда. 3-е уравнение Максвелла является обобщением закона Гауса для постоянных и переменных электро-магнитных полей: поток вектора через произвольную замкнутую поверхность S порождается свободным электрическим зарядом Q , находящийся в объеме V , ограниченный поверхностью S . В интегральной форме : 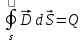 ; ; 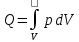 ; ; 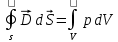 ; ;В дифференциальной форме : 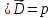 Дивергенция вектора D отлична от нуля в тех точках пространства где имеется свободные электрические заряды . В этих точках линии вектора D начинается на положительных зарядах ( источники поля ) и отрицательных зарядах ( стоки поля ) . 4-ое уравнение Максвелла называется законом непрерывности магнитных силовых линий : поток вектора магнитной индукции через любую замкнутую поверхность равен нулю . В интегральной форме : 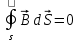 ; ; Не существет линий вектора B , которые только входят или выходят из замкнутой поверхности линии векторов B всегда пронизывают ее . векторное поле B не имеет источников , магнитные заряды не существуют . Линии магнитной индукции B непрерывны , они не имеют ни начала ни конца. В дифференциальной форме : 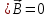 Одно из основных положений электромагнетизма состоит в том, что ни при каких условиях заряды не могут возникать или пропадать бесследно. Если в каких-либо условиях возникнет положительный заряд, то обязательно должен возникнуть и отрицательный заряд и, таким образом, суммарный заряд не изменяется. Этот факт называют законом сохранения заряда. Он приводит к уравнению непрерывности, сущность которого сводится к следующему. Если в некотором объеме изменяется плотность электрических зарядов во времени, то через поверхность, ограничивающую этот заряд, пойдет ток. Получим уравнение непрерывности из закона сохранения заряда. Интегральная форма уравнения непрерывности : Дифференциальная форма общего уравнения непрерывности : 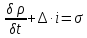 где 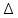 - дивергенция ; - дивергенция ; 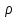 - количество величины q на единицу объёма (плотность величины q) - количество величины q на единицу объёма (плотность величины q) t- время ; i- плотность потока величины q ; 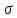 – добавление q на единицу объема в единицу времени . – добавление q на единицу объема в единицу времени . Вопрос 8 . Граничные условия для нормальных и касательных составляющих векторов Е, D. Соотношения показывающие связь между значениями составляющих векторов электро-магнитного поля в разных средах у поверхности раздела называется граничными условиями . Граничные условия для вектора электрической индукции 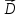 . .Рассмотрим границу раздела двух сред с различными диэлектрическими проницаемостями
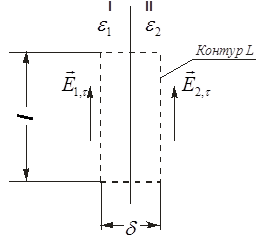
Элементарный цилиндр, выделенный на границе раздела двух сред для определения граничных условий на вектор электрической индукции. Согласно теореме Гаусса-Остроградского поток вектора электрической индукции Устремим высоту цилиндра к нулю Где Введем поверхностную плотность заряда: Если плотность поверхностного заряда равна нулю ( Мы можем сформулировать следующее важное утверждение: На границе раздела, не содержащей поверхностных зарядов, нормальная составляющая вектора электрической индукции непрерывна. Граничные условия для вектора напряженности электрического поля 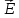 . .Рассмотрим снова границу раздела двух сред с различными диэлектрическими проницаемостями Где L — выбранный контур, L = 2 (1 +
Контур на границе раздела двух сред при определении граничных условий для векторов напряженности электрического поля. Устремим ширину контура Откуда следует, что Это равенство равносильно следующему утверждению: На границе раздела двух сред касательная составляющая вектора напряженности электрического поля всегда непрерывна. Вопрос 9 . Граничные условия для нормальных и касательных составляющих для векторов Н, В. Граничные условия для вектора напряженности магнитного поля 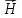 . .Выделим на границе раздела двух сред замкнутый контур L .
Воспользуемся законом полного тока Где Вдоль границы раздела может течь ток проводимости, тогда при стремлении Размерность поверхностной плотности тока [ Откуда следует, что : Это равенство равносильно следующему утверждению: На границе раздела двух сред разность касательных составляющих напряженности магнитного поля равна поверхностной плотности тока. При отсутствии поверхностного тока Это равенство равносильно следующему утверждению: На границе раздела двух сред, по которой не течет поверхностный ток, касательная составляющая магнитного поля непрерывна. Граничные условия для вектора магнитной индукции 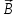 . .Рассмотрим границу раздела двух сред, обладающих различной магнитной проницаемостью. Принимая во внимание, что магнитных зарядов не существует, можно записать Это равенство равносильно следующему утверждению: На границе раздела двух сред нормальная составляющая вектора магнитной индукции всегда непрерывна. Вопрос 10 . Фазовая, групповая скорости и скорость распространения энергии . Фазовая скорость- это скорость с которой распространяется поверхность одинаковых фаз. В отсутствие дисперсии фазовая скорость волн не зависит от частоты. Поэтому, если есть набор волн разных частот, все они будут двигаться с одной и той же скоростью и пакет, который они образуют в результате сложения, при движении не изменяет своей первоначальной формы. Для волн, которые имеют дисперсию, кроме фазовой, необходимо ввести понятие групповой скорости. Групповая скорость характеризует распространение волн сложного несинусоидального характера в среде, где фазовая скорость волн зависит от их частоты. Групповая скорость волн — это скорость движения группы волн, которые образуют в каждый данный момент времени локализованный в пространстве волновой пакет. 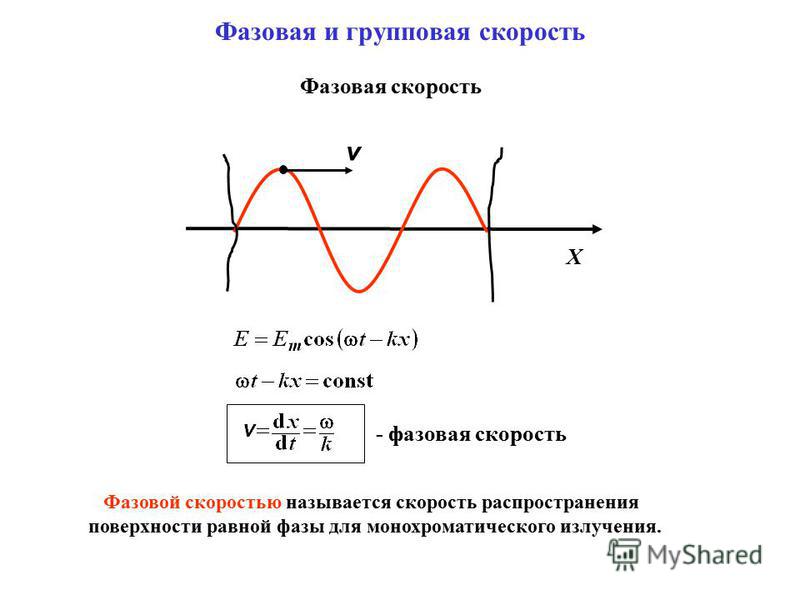  Групповая скорость обычно может быть интерпретирована как скорость распространения «энергии» волны и скорость, с которой могут быть переданы с помощью волнового пакета сигналы . Вопрос 11 . Тангенс угла диэлектрических потерь, критерий деления сред на проводники и диэлектрики. Диэлектрическими потерями называют энергию, рассеиваемую в электроизоляционном материале под воздействием на него электрического поля. Способность диэлектрика рассеивать энергию в электрическом поле обычно характеризуют углом диэлектрических потерь, а также тангенсом угла диэлектрических потерь. При испытании диэлектрик рассматривается как диэлектрик конденсатора, у которого измеряется емкость и угол δ, дополняющий до 90° угол сдвига фаз между током и напряжением в емкостной цепи. Этот угол называется углом диэлектрических потерь. При переменном напряжении в изоляции протекает ток, опережающий по фазе приложенное напряжение на угол ϕ (рис. 1), меньший 90 град. эл. на небольшой угол δ, обусловленный наличием активного сопротивления. 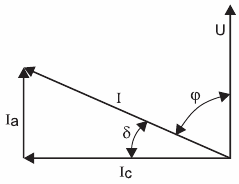 Рис. 1. Векторная диаграмма токов через диэлектрик с потерями: U — напряжение на диэлектрике; I — полный ток через диэлектрик; Ia,Ic — соответственно активная и емкостная составляющие полного тока; ϕ — угол фазного сдвига между приложенным напряжением и полным током; δ — угол между полным током и его емкостной составляющей Отношение активной составляющей тока Ia к емкостной составляющей Ic называется тангенсом угла диэлектрических потерь и выражается в процентах: 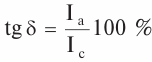 В идеальном диэлектрике без потерь угол δ=0 и, соответственно, tg δ=0. Увлажнение и другие дефекты изоляции вызывают увеличение активной составляющей тока диэлектрических потерь и tgδ. Поскольку при этом активная составляющая растет значительно быстрее, чем емкостная, показатель tg δ отражает изменение состояния изоляции и потери в ней. При малом объеме изоляции удается обнаружить развитые местные и сосредоточенные дефекты. {\displaystyle q} |