Законы Кеплера. Измерение расстояния и размеров тел Солнечной с. Законы движения планет

• Название: Законы движения планет
• Дата: 02.04.2023
• Размер: 310.73 Kb.
• Имя файла: Законы Кеплера. Измерение расстояния и размеров тел Солнечной с.docx
• Тип: Закон; #1032068

Законы движения планет (законы Кеплера). Определение расстояний до тел Солнечной системы и их размеров.

1 закон Кеплера. Орбита каждой планеты есть эллипс, в одном из фокусов которого находится Солнце.

а 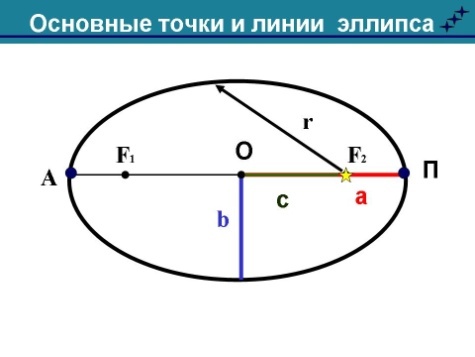– большая полуось эллипса, в – малая полуось эллипса, F_1, F₂ - фокусы

Перигелий (греч. пери – возле, около)- ближайшая к Солнцу точка орбиты планеты (для Земли 1-5 января).

Афелий (греч. апо – вдали) - наиболее удаленная от Солнца точка орбиты планеты (для Земли 1-6 июля).

Степень вытянутости эллипса характеризуется эксцентриситетом е

е = ,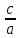

с – расстояние от центра до фокуса

При совпадении фокусов с центром (е=0) эллипс превращается в окружность, при е = 1, становится параболой, при е >1 – гиперболой.

планета	а	е	планета	а	е	карликовая планета	а	е
Меркурий	0,39	0,206	Юпитер	5,20	0,048	Плутон	39,52	0,253
Венера	0,72	0,007	Сатурн	9,54	0,054	Эрида	67,67	0,442
Земля	1,00	0,017	Уран	19,19	0,046	Седна	486,0	0,850
Марс	1,52	0,093	Нептун	30,07	0,008	Церера	2,80	0,089

2 закон Кеплера. Радиус-вектор планеты за равные промежутки времени описывает равные площади.

З 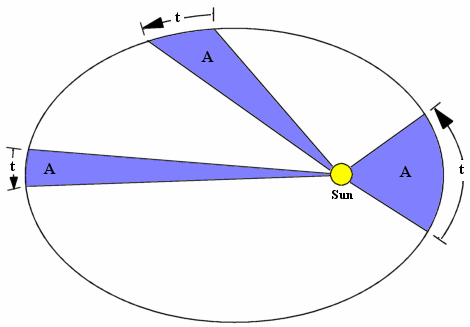аштрихованные площади фигур равны за равные промежутки времени. Из чертежа видно, что длины дуг разные, отсюда υ_п>υа, т.е в перигелии υ_max, а в афелии υ_min. Чем ближе планета к Солнцу, тем ее скорость больше.

   Самый близкий к Солнцу Меркурий обегает вокруг светила за 88 дней. За ним движется Венера, и год на ней длится 225 земных суток. Земля обращается вокруг Солнца за 365 суток, то есть ровно за один год. Марсианский год почти в два раза продолжительнее земного. Юпитерский год равен почти 12 земным годам, а далёкий Сатурн обходит свою орбиту за 29,5 лет! Словом, чем дальше планета от Солнца, тем продолжительнее на планете год. 

3 закон Кеплера. Квадраты звездных (сидерических) периодов обращения планет относятся между собой как кубы больших полуосей их орбит.

Т₁, а₁ – звездный период обращения и большая полуось одной планеты, а Т₂, а₂ – другой планеты

Большая полуось земной орбиты принята за астрономическую единицу расстояний:

1 а. е. = 149000000000 м. Звездный период Земли 1 год = 365 суток.

2. Определение расстояний до тел Солнечной системы и их размеров.

1. Геометрический метод (по параллаксам)

В – точка, в которой находится наблюдатель; А – доступная точка; С – недоступная точка АВ – базис (измеряется непосредственно)

Угол α, под которым из недоступного места виден базис, называется параллаксом

В пределах Солнечной системы в качестве базиса используют экваториальный радиус Земли

Е 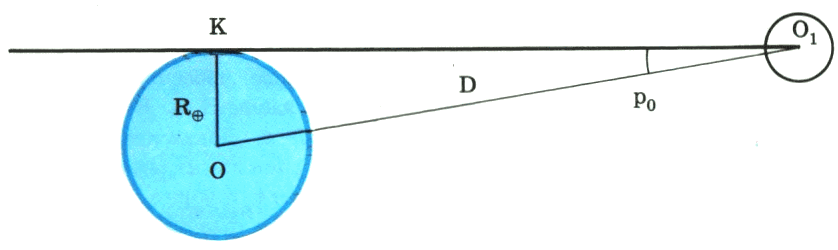сли горизонтальный параллакс найден, то расстояние до светила вычисляется по формуле: D=R/sin p₀

где D – расстояние от центра Земли до центра какого либо тела Солнечной системы;

R‒ экваториальный радиус Земли

Поскольку углы р₀ очень малы, то их синусы можно заменить самими углами, если величина угла выражена в радианах: sin p₀ ≈ p, но обычно р₀ выражено в секундах дуги, поэтому: 1 рад = 206265"

,

Р адиолокационный метод: Радиолокация заключается в том, что на небесное тело посылают мощный кратковременный радиоимпульс, а потом принимают отраженный сигнал. Зная скорость света в вакууме:

с = 299 792 458 м/с и точно измерив время прохождения сигнала туда и обратно, легко вычислить расстояние до небесного тела D = 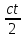. Радиолокационные наблюдения позволяют с большой точностью определять расстояния до небесных тел Солнечной системы. Этим методом уточнены расстояния до Луны, Венеры, Меркурия, Марса, Юпитера

Лазерная локация: Метод аналогичен радиолокации, однако точность гораздо выше. Лазерная локация позволяет определять расстояния между точками лунной и земной поверхности с точностью до сантиметров

2. Определение размеров тел Солнечной системы

При наблюдениях небесных тел Солнечной системы можно измерить угол ρ, под которым они видны земному наблюдателю. 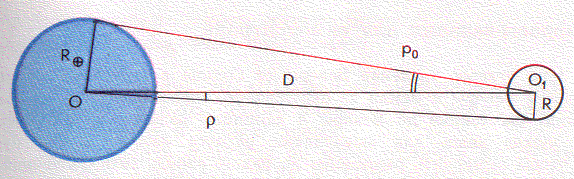Зная этот угловой радиус светила ρ и расстояние до светила D, можно вычислить линейный радиус R: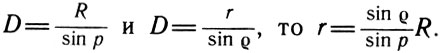



Е сли углы малы, то синусы пропорциональны углам можно написать:

Этот способ определения размеров светил применим только тогда, когда виден диск светила.

Задача. Определите расстояния: а) до Луны, если ее горизонтальный параллакс p = 57′; б) до Солнца, горизонтальный параллакс которого p = 8,8″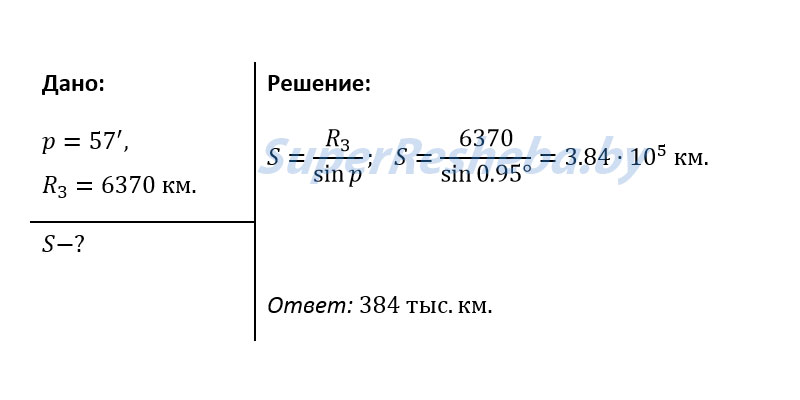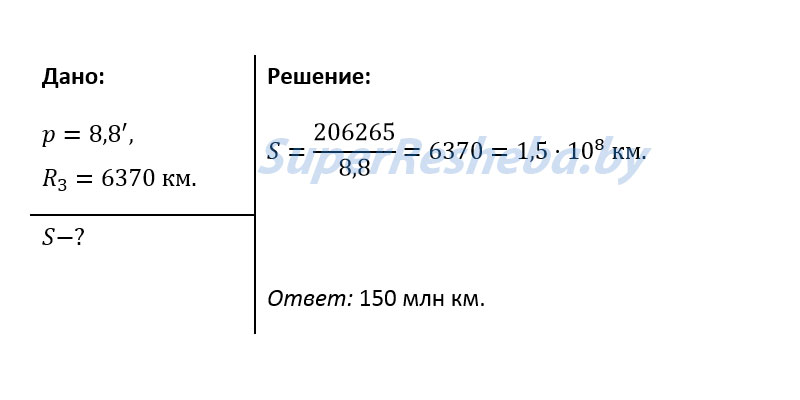



Задача. На каком расстоянии от Земли находится Сатурн, когда его горизонтальный параллакс равен 0,9"?



Задача. Чему равен линейный диаметр Луны, если она видна с расстояния 400 000 км под углом примерно 0,5°?