Законы фильтрации. Линейный закон фильтрации
 Скачать 415.19 Kb. Скачать 415.19 Kb.
|
|
1. Понятие о пористой среде. Важнейшие характеристики порового коллектора (пористость, просветность, проницаемость). Законы фильтрации. Линейный закон фильтрации (закон Дарси) Понятие о пористой среде Пористая среда – множество твердых частиц, плотно прилегающих друг к другу. Идеальный грунт – модель пористой среды, поровые каналы которой представляют пучок тонких цилиндрических трубок с параллельными осями. Фиктивный грунт – модель пористой среды, состоящая из шариков одинакового диаметра. Пористость фиктивного грунта по формуле Слихтера: 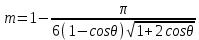 . . Э 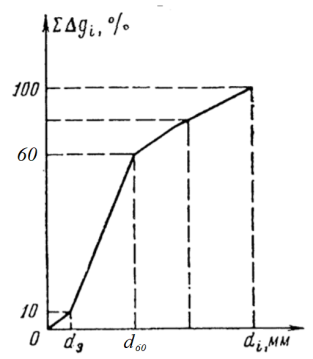 ффективный диаметр частиц dэ реального грунта – такой диаметр шаров, образующих эквивалентный фиктивный грунт, при котором гидравлическое сопротивление, оказываемое фильтрующейся жидкости в реальном и эквивалентном грунте, одинаково. Определяется в результате ситового анализа грунта (разделения на фракции). ффективный диаметр частиц dэ реального грунта – такой диаметр шаров, образующих эквивалентный фиктивный грунт, при котором гидравлическое сопротивление, оказываемое фильтрующейся жидкости в реальном и эквивалентном грунте, одинаково. Определяется в результате ситового анализа грунта (разделения на фракции). 1) Метод Газена: за dэ принимается такой диаметр d10, который соответствует 10% суммы масс всех фракций, при этом коэффициент неоднородности 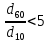 и dэ = 0,1-3 мм. и dэ = 0,1-3 мм.2) Метод Крюгера-Цункера: 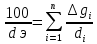 , где di – средний диаметр i-ой фракции, Δgi – масса i-ой фракции в % . , где di – средний диаметр i-ой фракции, Δgi – масса i-ой фракции в % .Важнейшие характеристики порового коллектора: Пористость – емкостная характеристика горных пород, численно равная отношению объема пустот ко всему объему породы. Размерность: доли единицы или проценты. Виды пористости поровых коллекторов: общая (учитывает все пустоты), открытая (сообщающиеся пустоты), эффективная (учитывает сообщ пустоты, содержащие нефть/газ, по которым возможно движение флюида). Коэффициент просветности – отношение площади просветов ко всей площади сечения образца 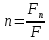 . .Проницаемость – это фильтрующий параметр горной породы, характеризующий её способность пропускать через себя жидкости и газы при перепаде давления. Законы фильтрации Движение флюида описывается линейным и, при его нарушении, нелинейными (двучленным, степенным) законами фильтрации. Линейный закон фильтрации (закон Дарси) Закон Дарси устанавливает линейную зависимость между объемным расходом Q несжимаемой жидкости и потерей напора (H2 – H1), приходящейся на единицу длины l. Формула для воды: 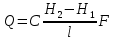 , где , где 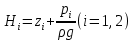 – полные напоры в начальном и конечном сечении образца; C – коэф. фильтрации [C] = м/с. Связь коэффициентов проницаемости и фильтрации: – полные напоры в начальном и конечном сечении образца; C – коэф. фильтрации [C] = м/с. Связь коэффициентов проницаемости и фильтрации: 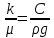 . .Формула для нефти: 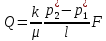 , где , где 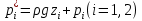 - давления, приведенные к плоскостям отсчета геометрических высот. В случае фильтрации нефти (и газа) необходимо разделить влияние свойств пористой среды (k) и жидкости (µ). - давления, приведенные к плоскостям отсчета геометрических высот. В случае фильтрации нефти (и газа) необходимо разделить влияние свойств пористой среды (k) и жидкости (µ).2. Дифференциальное уравнение движения. Закон Дарси в дифференциальной форме Основные уравнение подземной гидрогазодинамики: Уравнение движения идеальной жидкости Эйлера в проекции на ось 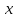 : :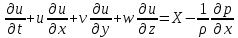 , где , где 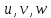 – проекции скоростей жидкой частицы; Х – проекция массовой силы, отнесенная к массе жидкости. – проекции скоростей жидкой частицы; Х – проекция массовой силы, отнесенная к массе жидкости.Уравнение неразрывности: 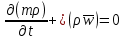 Уравнение количества движения: 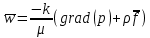 , где , где 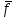 – вектор внеш. массовой силы. – вектор внеш. массовой силы.Закон Дарси в дифференциальном виде: 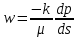 dp/ds – градиент давления; s – координата вдоль линии тока; Это фундаментальный закон фильтрации, устанавливающий связь между скоростью фильтрации и градиентом давления. Знак «-» означает, что течение флюида происходит в направлении, противоположном росту давлению. Учитывая, что w=Q/F, в зависимости от вида одномерного потока (от этого зависит площадь фильтрации) с помощью интегрирования диф-го уравнения Дарси можно получить соответствующие формулы. 3. Причины нарушения закона Дарси и пределы его применимости. Анализ и интерпретация экспериментальных данных Нижняя граница применимости закона Дарси для пористой среды Нижняя граница определяется проявлением неньютоновских реологических свойств жидкости и взаимодействием этой жидкости с твёрдым скелетом при малых скоростях фильтрации. Наиболее простой нелинейный закон фильтрации неньютоновских жидкостей: 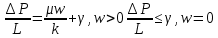 Верхняя граница применимости закона Дарси для пористой среды Верхняя граница его применимости обусловлена в большей степени образованием вихрей, вызывающих дополнительные вихревые сопротивления. Критерием движения служит число Рейнольдса Re, для фильтрации: 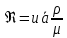 , где , где u – некоторая характерная скорость, 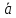 – линейный параметр, характеризующий среднее значение поровых каналов. – линейный параметр, характеризующий среднее значение поровых каналов. Щелкачев предложил взять за линейный параметр выражение, прямо пропорциональное 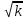 : : 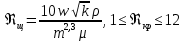 Миллионщиков предложил взять за характерную скорость среднюю скорость движения жидкости: 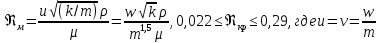 Закон Дарси выполняется, если Re меньше нижнего значения Reкр. Закон Дарси заведомо нарушен, еслиRe больше верхнего значения Reкр. 4. Нелинейные законы фильтрации При нарушении закона Дарси зависимость между скоростью фильтрации и градиентом давления лучше всего описывается двучленной формулой, выражающей плавный переход от линейного закона к нелинейному: 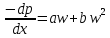 При малых значениях скорости 𝑎𝑤>>𝑏𝑤2 пренебрегаем вторым членом и получаем закон Дарси; при значениях w>wкр слагаемые 𝑎𝑤 и 𝑏𝑤2 имеют один и тот же порядок, при высоких скоростях фильтрации 𝑎𝑤<<𝑏𝑤2 и можно принять:  – формула Краснопольского – формула КраснопольскогоЧто соответствует квадратичному закону сопротивления и имеет место при фильтрации в крупнозернистых и трещиноватых породах. Коэффициенты a и b определяются либо экспериментально, либо по формуле a=µ/k, а b – приближенно по формуле, предложенной Ширковским:  Нелинейный закон фильтрации в дифференциальной форме можно записать в виде обобщенной двучленной формулы:  где 𝛽- константа пористой среды, определяемая экспериментально. Можно вывести перепад давления (депрессию): поставляем  , ,при dr→0 сечение трубки тока можно считать постоянным, поэтому запишем в виде  После интегрирования получаем зависимость давления в точке от ее удаления от оси скважины:  При достаточном удалении от скважины второй член в скобках стремится к нулю (1/r→0), поэтому:  , где , где  . .Степенной закон фильтрации  где  – константы, определяемые из опыта или по результатам исследования скважин. – константы, определяемые из опыта или по результатам исследования скважин.Наиболее простой нелинейный закон фильтрации неньютоновских жидкостей:  5. Уравнение Лейбезона для неустановившегося движения сжимаемой жидкости (газа) в пористой среде При выводе дифференциального уравнения Лейбензона предполагается, что коэффициенты пористости и проницаемости не изменяются с давлением, т.е. пласт недеформируемый, вязкость газа (флюида) также не зависит от давления:  Принимается также, что фильтрация газа (флюида) в пласте происходит по изотермическому закону, т.е. температура остается неизменной по времени. Для вывода дифференциального уравнения неустановившейся фильтрации совершенного (идеального) газа воспользуемся уравнением, которое справедливо для любого сжимаемого флюида: 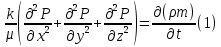 Функция Лейбензона для совершенного газа: 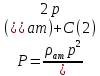 Продифференцируем выражение (2) по координатам 2 раза: 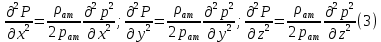 Считая 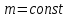 и учитывая, что для совершенного газа и учитывая, что для совершенного газа 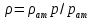 , получаем: , получаем: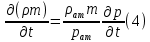 Подставим выражения (3) и (4) в уравнение (1), получим: 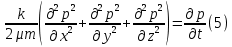 Выражение в скобке представляет собой оператор Лапласа относительно 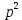 , поэтому уравнение (5) можно кратко записать в виде: , поэтому уравнение (5) можно кратко записать в виде: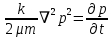 Полученное дифференциальное уравнение неустановившейся фильтрации совершенного газа называется уравнением Лейбензона и представляет собой нелинейное уравнение параболического типа. Оно справедливо при выполнении закона Дарси. 6. Функция Лейбензона. Уравнение неустановившейся фильтрации однородного флюида по закону Дарси Функция Лейбензона – функция, которая учитывает зависимость параметров жидкости и породы от давления. Вводится, когда одни из параметров (хотя бы один) зависит от давления. В общем виде функция Лейбензона выглядит: 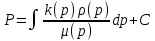 Функция Лейбензона для несжимаемой жидкости 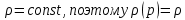 : :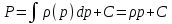 Функция Лейбензона для упругой (капельной) жидкости:   Функция Лейбензона для совершенного (идеального) газа:  Выведем уравнение неустановившейся фильтрации однородного флюида по закону Дарси, воспользовавшись уравнением неразрывности: Выведем уравнение неустановившейся фильтрации однородного флюида по закону Дарси, воспользовавшись уравнением неразрывности: Закон Дарси запишем следующим образом (в проекции на ось 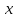 ): ): 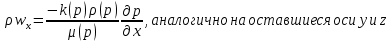 Далее запишем закон Дарси через функцию Лейбензона:  Подставим последнее выражение в уравнение неразрывности – получим дифференциальное уравнение неустановившейся фильтрации однородного флюида по закону Дарси: 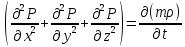 Если проницаемость пористой среды постоянна и постоянна вязкость флюида, то: 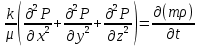 7. Модели одномерных фильтрационных потоков Уравнение Лапласа – дифференциальное уравнение установившегося движения несжимаемой жидкости:  Одномерным называется фильтрационный поток жидкости или газа, в котором скорость фильтрации, давление и др. характеристики течения являются функциями только одной координаты, отсчитываемой вдоль линии тока. 1) Одномерный плоскопараллельный поток между прямолинейным контуром питания и прямолинейной галереей стока:  . .2) Одномерный плоскорадиальный поток между круговым контуром питания и скважиной:  . .3) Радиально-сферический поток к скважине:  . .Оператор Лапласа для всех трех видов одномерного потока может быть записан с помощью единой формулы: 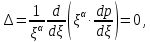 где показатель степени где показатель степени 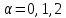 называется коэффициентом формы потока. называется коэффициентом формы потока. Однако, используя общую для всех трех случаев запись, нельзя получить универсальную форму представления решений, потому что интеграл, задающий распределение давления, вычисляется неоднозначно. • при 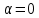 имеем прямолинейно-параллельное течение ( имеем прямолинейно-параллельное течение (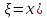 , ,• при  плоскорадиальное течение ( плоскорадиальное течение ( , ,• при  радиально-сферическое течение ( радиально-сферическое течение ( . .8. Основные формулы прямолинейно-параллельной фильтрации несжимаемой жидкости и совершенного газа 1) Для несжимаемой жидкости Из диф. З-на Дарси:  ; ;  Площадь фильтрации F=Bh (B – ширина пласта, h – высота пласта). Разделяя переменные, интегрируем:   , тогда объёмный дебит , тогда объёмный дебит 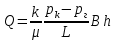 , где L – расстояние от контура питания до галереи. , где L – расстояние от контура питания до галереи.Распределение давления по длине пласта: 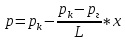 Время, в течение которого частица пройдёт путь длиной x: 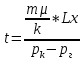 При безнапорном течении жидкости: 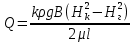 , H – полный напор на контуре или на галерее (формула учитывает приток только с одной стороны). , H – полный напор на контуре или на галерее (формула учитывает приток только с одной стороны).2) Для совершенного газа Вводится функция Лейбензона для совершенного газа: 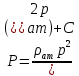 Если подставить в Q для жидкости при плоскопараллельном потоке 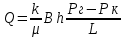 функцию Лейбензона вместо давления, то получится: функцию Лейбензона вместо давления, то получится:Массовый дебит совершенного газа 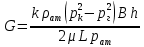 Распределение давления по пласту при плоскопараллельном потоке совершенного газа 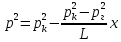 9. Основные формулы плоскорадиальной фильтрации несжимаемой жидкости и совершенного газа Запишем линейный закон фильтрации в дифференциальной форме (закон Дарси):  Для скважины  будет равно: будет равно:  подставим это в закон Дарси: подставим это в закон Дарси: Разделяя переменные, интегрируем: 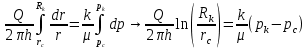 Далее выражаем объемный расход (дебит), получаем формулу Дюпюи: 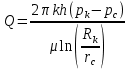 Найдем распределение давления по пласту: 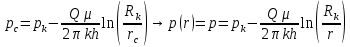 Вместо 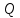 подставим ранее найденное выражение (формулу Дюпюи): подставим ранее найденное выражение (формулу Дюпюи):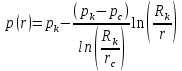 Получим закон для времени прохождения частиц в плоскорадиальном потоке: 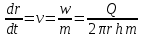 . Разделяем переменные и интегрируем: . Разделяем переменные и интегрируем: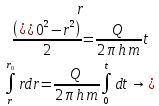 Выражаем требуемое время и подставляем вместо 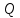 формулу Дюпюи: формулу Дюпюи: Формулы для совершенного газа можно получить, воспользовавшись функцией Лейбензона:   10. Основные формулы радиально – сферической фильтрации несжимаемой жидкости и совершенного газа Р  адиально-сферический поток. Траектории всех частиц жидкости – прямолинейные горизонтальные прямые, радиально сходящиеся к центру полусферического забоя. Такой поток может реализоваться, когда скважина вскрывает только плоскую горизонтальную, непроницаемую кровлю пласта. Пласт при этом должен быть неограниченной толщины, а забой иметь полусферическую форму. Приближение к данному виду потока тем лучше, чем глубина вскрытия меньше толщины пласта. адиально-сферический поток. Траектории всех частиц жидкости – прямолинейные горизонтальные прямые, радиально сходящиеся к центру полусферического забоя. Такой поток может реализоваться, когда скважина вскрывает только плоскую горизонтальную, непроницаемую кровлю пласта. Пласт при этом должен быть неограниченной толщины, а забой иметь полусферическую форму. Приближение к данному виду потока тем лучше, чем глубина вскрытия меньше толщины пласта.Основные формулы для жидкости Объемный дебит (расход), учитывая, что 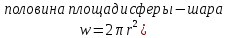 : :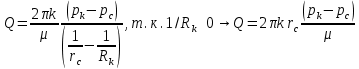 Распределение давление по пласту: 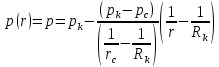 Время движения жидкой частицы по пласту: 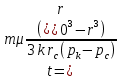 Основные формулы для совершенного (идеального) газа: Для этого записывается функция Лейбензона, которая подставляется вместо давления. 11. Основные формулы плоскорадиальной фильтрации несжимаемой жидкости по степенному закону Степенной закон фильтрации выглядит следующим образом: 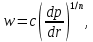 где 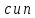 – константы, определяемые из опыта или по результатам исследования скважин. – константы, определяемые из опыта или по результатам исследования скважин.Найдем массовый расход (дебит) при плоскорадиальном течении: 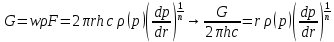 Возведем левую и правую части в степень 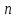 : : Проинтегрируем данное уравнение. Интеграл от левой части:   Интеграл от правой части уравнения: т.к. жидкость несжимаемая функция  может быть заменена может быть заменена 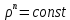 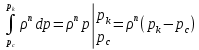 Таким образом, уравнение примет вид: 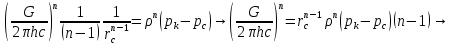 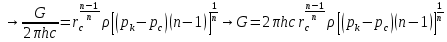 Объемный расход (дебит) получим, исключив из данной формулы плотность 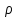 . .Найдем распределение давления по пласту: 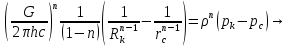 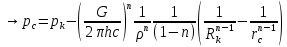 При этом: 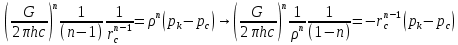 Получаем:    Рис. Индикаторные линии, соответствующие различным законам фильтрации жидкости Линейный закон фильтрации при  , нелинейные законы фильтрации: при , нелинейные законы фильтрации: при  и и  . .12. Основные формулы плоскорадиальной фильтрации несжимаемой жидкости по двучленному закону Нелинейный закон фильтрации в дифференциальной форме можно записать в виде обобщенной двучленной формулы:  где 𝛽- константа пористой среды, определяемая экспериментально. Можно вывести перепад давления (депрессию): поставляем  , ,при dr→0 сечение трубки тока можно считать постоянным, поэтому запишем в виде  После интегрирования получаем зависимость давления в точке от ее удаления от оси скважины:  Отсюда следует квадратичная (параболическая) зависимость депрессии от дебита, которая на индикаторной диаграмме изображается в виде параболы. При достаточном удалении от скважины второй член в скобках стремится к нулю (1/r→0), поэтому:  , где , где  . .Решая квадратное уравнение, приняв за переменную  , можно найти дебит скважины при двучленном законе фильтрации: , можно найти дебит скважины при двучленном законе фильтрации: 1  3. Основные формулы прямолинейно – параллельного потока несжимаемой жидкости в неоднородных пластах (слоисто-неоднородный пласт и зонально- неоднородный пласт) 3. Основные формулы прямолинейно – параллельного потока несжимаемой жидкости в неоднородных пластах (слоисто-неоднородный пласт и зонально- неоднородный пласт)С  лоистая неоднородность (неоднородность по толщине) – неоднородность в пласте, состоящем из нескольких изолированных пропластков различной мощности и проницаемости. Тогда объемный дебит для несжимаемой жидкости при плоскопараллельном течении: лоистая неоднородность (неоднородность по толщине) – неоднородность в пласте, состоящем из нескольких изолированных пропластков различной мощности и проницаемости. Тогда объемный дебит для несжимаемой жидкости при плоскопараллельном течении:  . Распределения давления по пропласткам идентично. . Распределения давления по пропласткам идентично.Зональная неоднородность (неоднородность по площади) – неоднородность в пласте, состоящем из последовательно расположенных зон различной проницаемости. Тогда объемный дебит для несжимаемой жидкости при плоскопараллельном течении:  . . Распределение давления представляет ломаную кривую с углом наклона обратно-пропорциональным проницаемости. Распределения давления:  (для плоскопараллельного потока). (для плоскопараллельного потока).14. Основные формулы плоскорадиального потока несжимаемой жидкости в неоднородных пластах (слоисто-неоднородный пласт и зонально-неоднородный пласт) Слоисто-неоднородный пласт – пласт, неоднородный по толщине. Дебит скважины в плоскорадиальном потоке при слоистой неоднородности определится путём сложения расходов каждого слоя:  . Распределение давления по пропласткам идентично. . Распределение давления по пропласткам идентично.Зонально-неоднородный пласт – пласт, неоднородный по площади. Тогда объемный дебит для несжимаемой жидкости при плоско-радиальном течении:  . Распределение давления представляет ломаную кривую с углом наклона обратно-пропорциональным проницаемости. Распределение давления: . Распределение давления представляет ломаную кривую с углом наклона обратно-пропорциональным проницаемости. Распределение давления:  (для плоско-радиального потока). (для плоско-радиального потока).15. Потенциал точечного источника и стока на плоскости Назовем точечным стоком на плоскости точку, поглощающую жидкость. Сток можно рассматривать как гидродинамически совершенную скважину бесконечно малого радиуса в пласте единичной толщины. Точечный источник – это точка, выделяющая жидкость (модель нагнетательной скважины). Определим потенциал скорости из выражения:  Причем функция потенциала скорости из закона Дарси:  Найдем потенциал точечного стока на плоскости. Так как точечный сток является моделью добывающей скважины и течение вокруг него плоскорадиальное, то можно воспользоваться формулой скорости фильтрации для такого потока:  После интегрирования получим выражение потенциала для точечного стока на плоскости:  С-постоянная интегрирования;  . .Таким образом, потенциал в окрестности скважины-стока пропорционален логарифму расстояния  от стока (центра скважины). При от стока (центра скважины). При  и и  функция функция  обращается в бесконечность, поэтому потенциал в этих точках теряет смысл. Для точечного источника справедливы все приведенные формулы, но дебит q считается отрицательным (q<0). Из формулы обращается в бесконечность, поэтому потенциал в этих точках теряет смысл. Для точечного источника справедливы все приведенные формулы, но дебит q считается отрицательным (q<0). Из формулы  следует, что линиями равного потенциала (эквипотенциалами) являются окружности следует, что линиями равного потенциала (эквипотенциалами) являются окружности  . .При работе в пласте нескольких скважин результирующий потенциал в точке М равен алгебраической сумме потенциалов, обусловленных работой каждой отдельной скважины.  Скорости фильтрации складываются геометрически. Это называется принципом суперпозиции. Используя этот принцип можно рассчитывать дебиты и потенциалы для нескольких скважин в пласте с удаленным контуром питания. Потенциал на контуре Фк и расстояние от скважин до контура одно и то же приблизительно равное  . .16. Приток жидкости к группе скважин в пласте с удаленным контуром питания. Потенциал на контуре питания:   Потенциал на забое 5-ой скважины:  Разность потенциалов между контуром питания и забоем 5-ой скважины:  Пусть дебиты скважин 1-4 равны между собой, но не равны дебиту 5-ой скважины:  Это же выражение для давлений:  Разность потенциалов между контуром питания и забоем 1-ой скважины:  Учитывая, что дебиты скважин 1, 2, 3 и 4 равны, тогда:  При равенстве дебитов скважин 1 и 5:   Дебит центральной газовой скважины в кусте:   17. Приток жидкости к скважине в пласте с прямолинейным контуром питания Для того, чтобы определить дебит скважины, расположенной в пласте с прямолинейным контуром питания, воспользуемся методом отображения источников и стоков, т.е. зеркально отобразим скважину-сток А (с дебитом  ) относительно контура питания и примем ее за скважину-источник А` (с дебитом ) относительно контура питания и примем ее за скважину-источник А` (с дебитом  ). ). Рис. Схема притока жидкости к скважине в пласте с прямолинейным контуром питания Потенциал в произвольной точке М:  Потенциал на контуре питания:  Потенциал на забое скважины А можно выразить следующим образом:  Тогда из последнего уравнения можем выразить  – дебит скважины-стока: – дебит скважины-стока: Преобразуем дебит скважины-стока, учитывая, что  : : 18. Приток жидкости к бесконечной цепочке (линейной батарее) скважин. Метод эквивалентных фильтрационных сопротивлений Рассмотрим приток к бесконечной цепочке скважин расположенных на расстоянии 2𝜎 друг от друга и расстоянии L от прямолинейного контура питания.  AB – главная линия тока (основной объем флюида); A’B’ – нейтральная линия тока (почти непроницаемая). Цепочка скважин отображается зеркально относительно контура питания в скважины-источники, и рассматривается интерференция двух цепочек скважин в неограниченном пласте. Вдоль АВ – частицы жидкости будут наиболее быстрее передвигаться. Прямые A’B’ (нейтральные линии тока) – можно рассмотреть как непроницаемые пласты. Дебит каждой скважины бесконечной цепочки определяется следующим образом:  Тогда суммарный дебит всех скважин прямолинейной цепочки:  Для решения данной задачи также используют метод эквивалентных фильтрационных сопротивлений Борисова. Сопротивление в данном случае складывается из внешних (потери при перемещении жидкости к цепочке от контура питания – 𝜌) и внутренних (потери на перераспределение по скважинам в цепочке – 𝜌’):  Тогда формулу дебита для одной прямолинейной цепочки можно записать в виде (суммарный):  Схема фильтрационных сопротивлений притока к двум прямолинейным цепочкам скважин:  рk - рc1 = (𝑄’1 + 𝑄’2) ⋅ 𝜌1 + 𝑄’1 ⋅ 𝜌’1 рk - рc2 = (𝑄’1 + 𝑄’2) ⋅ 𝜌1 + 𝑄’2 ⋅ 𝜌2 + 𝑄’2 ⋅ 𝜌’2 19. Приток жидкости к кольцевым батареям скважин. Метод эквивалентных фильтрационных сопротивлений Вывод формул внешнего и внутреннего сопротивлений:   Предполагается, что расстояние между двумя скважинами 2σ, глубина вскрытия, радиус скважин в батарее одинаковые.  Внешнее сопротивление i-ой батареи  Половина расстояния между скважинами в i-ой батарее:  Внутреннее сопротивление i-ой батареи  Аналогия с электрическим током pк, pc1, pc2 - «потенциалы φ» (pк - pc1) и (pк - pc2) - «разность потенциалов», или «напряжение U» ρ1, ρ2 – «внешнее сопротивление R» ρ’1, ρ’2 – «внутреннее сопротивление r» Q1 и Q2 - «сила тока I» Закон Ома I = U / R или U = IR По этой аналогии записываем систему уравнений:  Метод позволяет определить оптимальный радиус, на котором должны стоять друг от друга скважины, чтобы давать наибольший дебит. 20. Характеристика потока в условиях нелинейного закона фильтрации При нарушении закона фильтрации Дарси зависимость между скоростью фильтрации (w) и градиентом давления (dp/dx) лучше всего описывается двучленной формулой, выражающей плавный переход от линейного к нелинейному закону:  , где , гдекоэффициенты a и b определяются экспериментально либо по формулам:  . .Причины нарушения линейного закона Дарси: появление инерционных сопротивлений; возникновение турбулентного режима течения; образование вихрей, вызывающих дополнительные вихревые сопротивления (главная). При малой скорости aw>>bw2 пренебрегаем вторым членом и получаем линейный закон Дарси. При w>wкр слагаемые aw и bw2 имеют одинаковый порядок. При больших скоростях фильтрации aw<  (формула Краснопольского). (формула Краснопольского).Нелинейный (двучленный) закон фильтрации в диф форме можно записать в виде обобщенной двучленной формулы  где β – константа пористой среды, определяемая экспериментально. где β – константа пористой среды, определяемая экспериментально.Двучленный закон выражен зависимостью  или упрощенно или упрощенно  , где , где  . Отсюда следует квадратичная (параболическая) зависимость депрессии от дебита, которая на индикаторной диаграмме изображается в виде параболы. . Отсюда следует квадратичная (параболическая) зависимость депрессии от дебита, которая на индикаторной диаграмме изображается в виде параболы. |
