Законов идеальных растворов учитывается при помощи расчетной величины активности (Г. Льюис)

• Название: Законов идеальных растворов учитывается при помощи расчетной величины активности (Г. Льюис)
• Дата: 12.04.2022
• Размер: 0.69 Mb.
• Имя файла: Voprosy_30-33.docx
• Тип: Закон; #466971

30. Способы определения коэффициента активности реальных растворов неэлектролитов.

В неидеальных растворах (жидких и твердых) отклонение от законов идеальных растворов учитывается при помощи расчетной величины — активности (Г. Льюис).

Зависимость химического потенциала μ_i компонента в идеальном растворе от молярной доли х_i,

этого компонента в растворе выражается уравнениями:

dμ_i= RT d ln x_i ; (1)

μ_i=μ^*_i+RT ln x_i ; (2)

μ_i,2=μ_i,1+RT ln(x_i,2/x_i,1) ; (3)

где μ^*_i — химический потенциал чистого i-го компонента (х_i= 1); μ^*_i зависит от температуры, давления и природы вещества; μ_i,1 и μ_i,2 — значения μ_i в 1-м и 2-м состояниях.

Для вычисления химического потенциала i-го компонента в неидеальном растворе в (1) — (3)

вместо концентрации (молярной доли) подставляется активность a_i i-го компонента: dμ_i= RT d ln a_i ; (4)

μ_i=μ⁰_i+RT ln a_i ; (5)

μ_i,2=μ_i,1+RT ln(a_i,1/a_i,2) ; (6)

где μ⁰_i — стандартный химический потенциал. В стандартном состоянии активность принимают равной единице, a⁰_i = 1. Активностью ¡-го компонента раствора называется величина, которую

нужно подставить в выражение для химического потенциала компонента в идеальном растворе, чтобы получить действительное значение химического потенциала ¡-го компонента в

неидеальном растворе. Коэффициентом активности называется отношение активности

компонента в растворе к его концентрации.

Равновесные свойства неидеальных растворов зависят от активности растворителя или растворенного вещества. Рассмотрим несколько способов определения активности или

коэффициента активности растворителя и растворенного вещества в неидеальных растворах.

Активность зависит от выбора стандартного состояния. Определение активности летучего растворенного вещества по парциальному давлению его пара.

1. 
   По парциальному давлению. Используя закон Рауля
   

p₁=p⁰₁ a₁ p₁=p⁰₁ γ₁x₁

γ₁=p₁/ p⁰₁x₁ Активность используется только для растворов, не для газов!

p₂=k*a₂

p₂=k γ₂x₂(x₂/p₂)

γ₂=p₂/ p^ϴ₂ x₂

2. 
   По константе распределения (закон Нернста)
   

Этот метод используется только в том случае, если вещество распределенное между двумя фазами α и β образует в одной фазе идеальный раствор, а в другой реальный.

K=x_Д^α/а_Д ^β

а_Д ^β= x_Д^α/К

γ_Д ^β= х_Д ^α/х_Д^β К

3. 
   По криоскопическим данным
   

^𝑀1(Т,тв)

= 𝑀^∅ + 𝑅𝑇𝑙𝑛а


1(𝑇,ж)

1
∆𝐻𝑚,пл ∗ ∆Т

−𝑙𝑛𝑎₁ =


𝑅𝑇²пл

Возьмем производную

∆𝐻𝑚, пл 𝑑∆𝑇

−𝑑𝑙𝑛𝑎₁ =


𝑅𝑇²пл

Вспомним 2 −оеуровнениеГиббса-Дюгема

𝑛₁𝑑𝑀₁ + 𝑛₂𝑑𝑀₂ = 0


1
𝑀₁ = 𝑀^∅ + 𝑅𝑇𝑙𝑛а₁


2
𝑀₂ = 𝑀^∅ + 𝑅𝑇𝑙𝑛а₂

𝑑𝑀₁ = 𝑅𝑇𝑙𝑛а₁

𝑑𝑀₂ = 𝑅𝑇𝑙𝑛а₂

𝑛₁𝑑𝑙𝑛𝑎₁ + 𝑛₂𝑑𝑙𝑛𝑎₂ = 0

−𝑛₂

𝑑𝑙𝑛𝑎 = 𝑑𝑙𝑛𝑎

1 _𝑛1 2

Подставляю ⁽2⁾в⁽1⁾

^𝑛2 𝑑𝑙𝑛𝑎

_𝑛1 2

∆𝐻𝑚, пл 𝑑∆𝑇

⁼ 𝑅𝑇²пл

𝑑𝑙𝑛𝑎<sub>2

=</sub> ∆𝐻𝑚,пл∗𝑛_{1 ∗ 𝑑∆𝑇}

𝑅𝑇²пл∗ 𝑛₂

𝑛₂

= 𝑚₂

⁽моляльность⁾ {^моль}

кгр−ля

𝑛₁ =

1000


М₁

∆𝐻𝑚,пл ∗ 1000

1
𝑑𝑙𝑛𝑎₂ = _{𝑅𝑇2пл 𝑀}

∗ 𝑚₂

𝑑∆𝑇

𝑑𝑙𝑛𝑎₂

= ^𝑑∆𝑇 (3)

𝑘_𝑓𝑚₂

Введем вспомогательную величину

j=1-^∆𝑇

𝑘_𝑓∗𝑚₂

-возьмемпроизводную ^{𝐾𝑓∆𝑇𝑑𝑚2}


1
𝐾²𝑚₂∗𝑚₂

𝑑𝑗 = −

^{𝑘𝑓 ∗ 𝑚2𝑑∆𝑇 − 𝐾 + ∆𝑇𝑑𝑚2} −𝑑∆𝑇

𝐾² ∗ 𝑚^{2 =} 𝐾 𝑚 ⁻

∆𝑇𝑑𝑙𝑛𝑚₂


𝐾 𝑚

𝑓 2

𝑓 2

𝑓 2

dj=−𝑑𝑙𝑛𝑎₂ + 𝑑𝑙𝑛𝑚₂ − 𝑗 ∗ 𝑑𝑙𝑛𝑚₂

𝑑𝑗 = −𝑑𝑙𝑛𝛾₂

− 𝑑𝑙𝑛𝑛₂

+ 𝑑𝑙𝑛𝑚<sub>2

−</sub> 𝑗𝑑𝑚₂

𝑚₂

_∫𝑚₂

^{𝑗 𝑚}₂ 𝑗𝑑𝑚₂

_𝑚2=0 𝑑𝑙𝑛𝛾₂ = − ∫₀ 𝑑𝑗 − ∫₀
𝑚₂

проинтегрируем

𝑙𝑛𝛾₂

𝑚₂

= −𝑗 − ^{∫ 𝑗}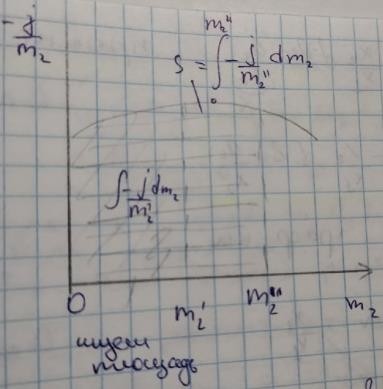

𝑚₂

0
𝑑𝑚

4. 
   Определение активности растворителя (растворенного вещества) по активности растворенного вещества (растворителя)
   

X₁dϻ₁+x₂dϻ₂=0 ϻ₁=ϻ₁⁰+RT lnγ₁+ RT lnx₁ ϻ₂=ϻ₂^ϴ+RT lnγ₂+ RT lnx₂ dϻ₁=RTd lnγ₁+ RT d lnx₁

x₁ lnγ₁+x₁ d lnx₁ + x₂ lnγ₂+ x₂ lnx₂=0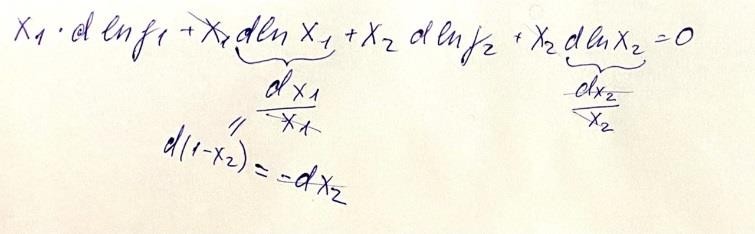




𝑑⁽1 − 𝑥₂⁾ = 𝑑𝑥₂

X₁ d ln γ₁ + x₂ d ln γ₂ = 0

^∫𝑑 𝑙𝑛𝛾1 = ^∫− 𝑥2 ∗ 𝑥1 ∗ 𝑑 𝑙𝑛 ^𝑎2

𝑥2

ln γ₁= ∫ − ^𝑥2 𝑑 𝑙𝑛 ^𝑎2

𝑥1 𝑥2

30. Правило фаз Гиббса (понятие фазы, вариантности системы, компонента системы).

Правило фаз(или правило фаз Гиббса) —выражает основной закон фазового равновесия и устанавливает связь в равновесной системе между числом фаз (Ф), числом компонентов (К), которые присутствуют во всех фазах, и числом независимых термодинамических параметров (вариантностью системы С).
Общее число параметров системы, характеризующих концентрацию, равно К • Ф. величина р, какого- либо компонента в данной фазе равна его химическому потенциалу во всех остальных фазах, то количество независимых уравнений для

этого компонента равно Ф - 1. Очевидно, что для всех компонентов системы оно будет равно К(Ф - 1). Для каждой фазы существует одно уравнение состояния; значит, для системы число таких уравнений равно Ф.
Таким образом, общее число уравнений, связывающих параметры, равно К(Ф - 1) + Ф. Разность между числом параметров и числом связывающих их уравнений равно числу независимых параметров системы (С).
F=К – Ф +2

К- количество компонентов; Ф- количество фаз; F - Число степеней свободы; 2- T и P внешние факторы (С)

число степеней свободы (F) возрастает с увеличением числа независимых компонентов (К) и уменьшается при росте числа фаз (Ф). При F = 0 в равновесии находится наибольшее число фаз. В общем случае, число фаз не может быть больше К + C (при этом F = 0): Ф  К  C. Например, для однокомпонентной (К = 1) системы при изменении двух внешних факторов температуры и давления (C = 2), максимальное количество фаз равно трем (твердая, жидкая и газообразная).

Правило фаз Гиббса для однокомпонентной системы: в равновесной термодинамической системе, на которую из внешних факторов оказывают влияние только температура и давление,

число термодинамических степеней свободы равно числу компонентов минус число фаз плюс два.

F  К Ф  2

Для двухкомпонентной системы (F = 2) диаграммы рассматривают без учета газовой фазы, то есть считают, что р = const, а изменяющимся внешним фактором считают только температуру(C=1).

Тогда правило фаз Гиббса запишется следующим образом: С  2Ф 1 3Ф. Правилу фаз Гиббса не подчиняются коллоидные системы, в которых дисперсная фаза микроскопических размеров. Правило фаз не применимо к неравновесным метастабильным состояниям (переохлажденная вода, перегретый пар и т.д.).


i
При фазовом равновесии химические потенциалы каждого компонента равны во всех фазах  ⁽¹⁾=


i i
 ⁽²⁾= ..=  ^(p) i= 1, 2, .., C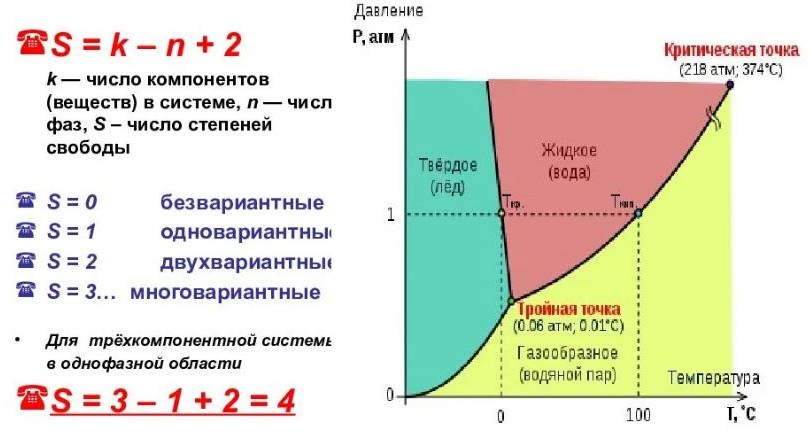

30. Термодинамическое условие стабильности фаз и фазового равновесия.

В состоянии равновесия может находиться система, состоящая из нескольких различных по своим физико-химическим свойствам фаз, пространственно разделенных не изменяющимися с течением времени (или для квазиравновесного случая бесконечно медленно изменяющимися) границами раздела фаз. Если через эти границы не происходит макроскопический перенос, а сами фазы находятся в состоянии

термодинамического равновесия, то такая термодинамическая система, несмотря на свою неоднородность, будет находиться в состоянии термодинамического равновесия.

Для равновесия фаз необходимо, чтобы между ними наблюдалось тепловое и механическое равновесие. Первое из этих условий означает равенство температур и с разных сторон границы раздела фаз: . Второе

условие не обязательно соответствует равенству давлений и с разных сторон границы раздела, так как сама эта граница, в случае, если её форма не представляет собой плоскости, может создавать дополнительное межфазное

давление . Поэтому в общем случае условие механического равновесия

имеет вид:
,

где: - дополнительное давление на первую фазу, создаваемое границей её раздела со второй. Если считать границы раздела фаз плоскими, то условие станет эквивалентным предположению о равенстве давлений по обе стороны

.

Термодинамическим критерием фазового превращения – является неравенство химических потенциалов; вещество из фазы с большим хим потенциалом будет самопроизвольно переходить в фазу с меньшим хим потенциалом

30. Диаграммы состояния в однокомпонентной системе. Уравнение Клаузиуса-Клайперона.

В состоянии фазового равновесия: ϻ^α =ϻ^β при Т, Р=CONST (1)
При изменении температуры на б.м. величину d T, давление на б.м. dp, устанавивается новое фазовое равновесие ϻ^α +d ϻ^α =ϻ^β + d ϻ^β (2)

Из (1) и (2) следует d ϻ^α= d ϻ^β

Т.k. ϻ=g то : ϻ^α =-S^αd T+ V^αdp

ϻ^β=-S^βd T+ V^βdp

→ -S^αd T+ V^αdp=-S^βd T+ V^βdp

_→ 𝒅𝒑 ₌ ∆𝑺ф.п. ₌ ∆Н𝒎,ф.п.

𝒅𝑻 ∆𝑽ф.п. Т∆𝑽ф.п.

𝒅𝒑₌∆Н𝒎,ф.п.

Уравнение Клайперона

𝒅𝑻 Т∆𝑽

1. 
   тв→ж
   

𝒅𝒑₌ ∆Н𝒎,пл

𝒅𝑻 Т(𝑽ж−𝑽тв)

Каждая точка лежащая на (о-а) характеризует равновесие 2х фаз тв и ж К1=1-2+2=1 система моновариантна

К2=1-1+2=2 система бивариантна

2. 
   ж→п
   

𝒅𝒑₌ ∆Н𝒎,исп _{𝑽п ≫ 𝑽ж}

𝒅𝑻 Т⁽𝑽п−𝑽ж⁾

Каждая точка лежащая на (о-в) –равновесие двух фаз ж и п

Для ф.п. ж-п для высоких V и T существует особая точка, которая называется критической

В критическом положении ж и п фазы тождественны и они переходят друг в друга без границы раздела, без мениска

В области крит. Т. Вещество обладает уникальными свойствами. Оно имеет сжимаемость как у газа, а плотность как у жидкости

В кр. Т. Fк= 1-2+2-1=0 (на нее повлиять нельзя)

3. 
   тв→п (возгонка, сублимация)
   

𝒅𝒑₌ ∆Н𝒎,субл _{> 𝟎}

𝒅𝑻 Т⁽𝑽п−𝑽тв⁾

Т. О – называется тройной. В ней в равновесии 3 фазы одновременно К₀=1-3+2=0 (ей также нельзя управлять)

Наклон кривых ОА, ОВ, ОС на плоской диаграмме состояния определяется знаком и величиной производной dP/dT, выражаемой уравнением Клапейрона-Клаузиуса.

Определение термодинам. Хар-к фаз. Перехода ж-п

𝒅𝒑₌∆Н𝒎,исп

𝒅𝑻 Т⁽𝑽п⁾

При переходе из уравнения Клаперона в ур Калузиуса-Клаперона:

1. 
   Vmп>>Vmж → Vmж пренебрегаем, след. Vп=Vж
   
2. 
   Считаем, что пар ведет себя как идеальный газ и можно использовать ур-е состяния идеального газа: Pv=RT→V=RT/p
   
3. 
   Считаем, что мольная энтальпия испарения (Нm.исп) является независимой от Т
   

_След. 𝒅𝒑₌∆Н𝒎,исп∗𝒑 _→𝒅𝒑₌∆Н𝒎,исп∗𝒑 _𝒅𝑻

𝒅𝑻

𝑹𝑻^𝟐

𝒑 𝑹𝑻^𝟐

52. 
    Последовательная Реакция первого порядка с общим реагентом
    

Две стадии называются последовательными, если вещество, образующееся в первой стадии, является исходным реагентов во второй. Если обе стадии первого порядка, то мы имеем дело с последовательной реакцией первого порядка:



При этом по условию материального баланса сумма текущих концентраций всех участников

реакции равна начальной концентрации исходного реагента: [A] + [B] = [C] = [A]0 (4) Наша задача – выразить в явном виде концентрации всех веществ: реагента А, промежуточного продукта В,

конечного продукта С. Что касается реагента А, то затруднений нет, поскольку дифференциальное уравнение (1) совпадает с уравнением простой реакции первого порядка. Это уравнение мы не раз интегрировали:

Как видно из представленных графических зависимостей, концентрация реагента А изменяется по классической экспоненте, концентрация продукта С монотонно возрастает, стремясь к начальной концентрации реагента. Зависимость концентрации промежуточного продукта В имеет вид

кривой с экстремальной точкой М, которой соответствует максимальная концентрация вещества [В]. Скорость накопления вещества В в точке М равна скорости его расходования, а общая

скорость изменения концентрации В равна нулю. Найдем координаты точки М, для чего

продифференцируем уравнение (13) и приравняем дифференциал к нулю.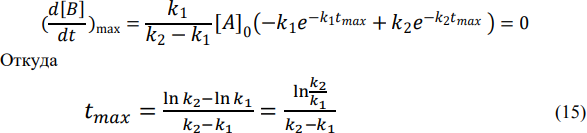

52. 
    Приближенные методы в анализе кинетических схем хим реакций. Метод Боденштейна и квазиравновесного приблежения.
    

Для большинства реакций, содержащих несколько элементарных стадий, кинетические уравнения могут быть достаточно сложными. Вместе с тем, константы скорости отдельных стадий могут сильно различаться, что позволяет использовать при решении кинетических уравнений

приближенные методы. Наиболее часто используется метод квазистационарных концентраций (метод Боденштейна) Анализ уравнений (15) и (16) показывает, что при k2>>k1 и при увеличении соотношения k2/k1 значение [В]мах и время его достижения (tмах) уменьшаются. Это можно

показать непосредственно расчетным методом. Зададим в последовательной реакции первого порядка [A]₀ = 0,1 M, k₂ = 1,0 c^-1 , k₁ = 0,1 c^-1 , т.е. различие в константах скорости не слишком

большое k2/k1 = 10. Подставляем эти значения в уравнения (15) и (16).




А теперь предположим, что константы скорости второй и первой стадий отличаются в 1000 раз, т.е. промежуточное вещество В образовалось в первой стадии и, являясь очень

реакционноспособным, сразу же превращается в продукт С: [A] ₀ = 0,1 M, k₂ = 100 c^-1 , k₁ = 0,1 c^-1 ,

т.е. различие в константах скорости большое k2/k1 = 1000.



Как видно из расчетов, чем более реакционноспособным является промежуточное вещество, тем меньше его максимальная концентрация и тем меньше время достижения этой концентрации:




Подобный анализ позволяет в первом приближении считать, что скорость накопления промежуточного продукта при условии его высокой реакционной способности равна 0. Другими словами, промежуточное вещество образуется в первой стадии с некоторой константой скорости k₁ и сразу же в силу своей высокой реакционной способности вступает во вторую стадию с существенно большей скоростью. В этом физическая основа метода квазистационарного

приближения, или Боденштейна.

В связи с чем концентрация промежуточного вещества в любой момент времени мала (но не равна нулю), а, следовательно, мала и скорость ее изменения, которую принимают равной нулю. Так, в соответствии с методом квазистационарного приближения скорость накопления промежуточного продукта B при условии его высокой реакционной способности равна

приближенно нулю: d[В]/dt≈ 0 . Поскольку с математической точки зрения нулю равна производная от постоянной величины, то это приближение часто называют стационарным. В качестве примера использования этого метода рассмотрим следующую схему реакции:
(17)

В соответствии со схемой (17) скорость реакции определяем по накоплению продукта П. Продукт образуется в элементарной стадии с константой скорости k2. Поскольку на основании постулатов химической кинетики каждая элементарная стадия сложной реакции протекает независимо и к

каждой элементарной стадии можно применить основной постулат химической кинетики, то
кинетическое уравнение для схемы (17) можно записать

В конечном виде кинетического уравнения не должно быть никаких промежуточных продуктов, т.е. должны быть только концентрации реагентов. В связи с чем, все приближенные методы

анализа кинетических схем направлены на то, чтобы так или иначе выразить концентрации промежуточных продуктов через концентрацию исходных веществ.

В методе Боденштейна задача сводится к тому, чтобы правильно написать скорость накопления промежуточного продукта. Каждую элементарную стадию схемы считаем независимой и к

каждой стадии применяем основной постулат химической кинетики. Так, в соответствии со схемой реакции вещество В образуется на стадии с константой скорости k₁. Скорость образования на основании основного постулата химической кинетики равна k₁[А]. Расходуется промежуточное вещество В на стадии с константой скорости k_-1, скорость убыли вещества В на этой стадии равна - k-1[В]. Также вещество В расходуется на элементарной стадии с константой скорости k2. Скорость убыли вещества В на этой стадии равна –k₂[В].

Тогда суммарная скорость накопления промежуточного продукта В будет слагаться из скорости его образования в первой стадии и скоростей его убыли во второй стадии и стадии, обратной первой. И эта скорость в методе квазистационарного приближения равна приблизительно нулю:
(18)

Поскольку правая часть уравнения (18) стала определенной, равной 0, то уравнение (18) можно решить относительно неизвестной концентрации промежуточного продукта:




Другим приближенным методом в химической кинетике является метод квазиравновесного приближения. В квазиравновесном приближении принимается, что равновесие в обратимых стадиях достигается значительно быстрее, чем промежуточные соединения вступают в дальнейшие превращения (k-1 >> k2).

На этом основании можно считать, что концентрация промежуточного соединения во времени
равна практически равновесной, определяемой уравнением , (20) где [В]_квазир, [А]_квазир – квазиравновесные концентрации в данный момент времени; K– константа равновесия первой обратимой стадии.

Квазиравновесные концентрации – это такие концентрации реагентов, которые определяются константой равновесия, но не в равновесном, а в любом другом моменте времени. В методе

квазиравновесного приближения концентрацию промежуточного продукта В выражаем через константу химического равновесия в соответствии с уравнением (20): [В]_квазир = К [А]_квазир, где [А]_квазир равна аналитически определяемой концентрации реагента А. Выражая концентрацию промежуточного соединения В через константу равновесия, имеем V=k₂ K[A]=(k₂k₁/k_-1)*[A]. (21)

Задача. Используя метод Боденштейна, найдите уравнение скорости образования фосгена (COCl2) согласно следующему механизму: