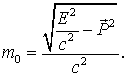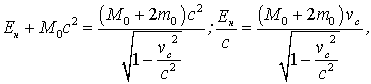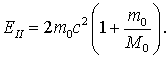физика 16-30. Закону Гука где k коэффициент жёсткости системы

• Название: Закону Гука где k коэффициент жёсткости системы
• Анкор: физика 16-30.docx
• Дата: 19.03.2018
• Размер: 244.54 Kb.
• Имя файла: физика 16-30.docx
• Тип: Закон; #16900
• страница: 4 из 4

8.6. Релятивистские инварианты. Закон сохранения энергии-импульса

     Определим величины, сохраняющиеся при переходе из одной системы отсчета в другую. Их обычно называются инвариантами. Как отмечалось, 4-импульсу  соответствует инвариант

     



     Подставляя значение  получаем

     

(8.15)

     Это соотношение между релятивистской энергией и релятивистским импульсом выполняется как для частицы" так и для тела, и даже для сложной системы, так как при его выводе нигде не использовалась неделимость объекта.

     И общем случае в (8.15) под Е следует понимать полную энергию системы, а под  - геометрическую сумму импульсоввсех частей системы.

     Равенство (8.15) можно рассматривать так же как определение инвариантной массы (массы покоя) любой физической системы

     

(8.16)

     В частном случае системы отсчета, в которой импульс равен нулю (), имеем

     

(8.17)

     Следовательно, масса покоя тела определяет его энергию покоя (во всех ее видах). В релятивистской механике, в отличие от классической, энергия тела всегда положительна.

     В другом частном случае, когда масса покоя равна нулю,  соотношение (8.15) дает связь между релятивистским импульсом и энергией следующего вида

     



     В частности, для для фотона с нулевой массой покоя эта формула преобразуется к виду

     



     Весьма необычное свойство инвариантной массы (массы покоя) в теории относительности видно из следующих примеров.

     Пример 1 . Система состоит из двух одинаковых фотонов, движущихся в одном направлении. Согласно(8.12)масса покоя этой системы равна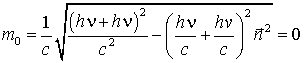

     

,

     где- единичный вектор в направлении движения фотонов. Результат достаточно тривиальный: масса покоя каждого фотона равна нулю, и масса покоя системы двух фотонов также равна нулю. Свойство аддитивности массы покоя в этом частном случае соблюдается.

     Пример 2 . Система состоит из двух одинаковых фотонов, которые движутся в противоположных направлениях. Имеем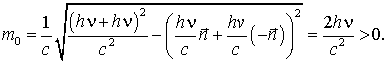

     



     Результат не тривиальный. В более общей форме это означает, что электромагнитное излучение общего вида, когда фотоны разлетаются в различных направлениях под различным углами, обладает положительной массой покоя, хотя масса покоя отдельных фотонов и равна нулю. Отсюда также следует, что подобное электромагнитное излучение создает гравитационное поле и, разумеется, само испытывает на себе воздействие со стороны внешнего гравитационного поля.

     Вернемся к рассмотрению 4-импульса 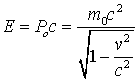. Он объединяет релятивистскую энергию  с релятивистским импульсом 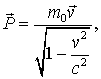 а значит представляет собой некоторую новую (одну единую!) величину, которую можно определить термином энергия-импульс. 4-вектору энергия-импульс соответствует инвариант (8.15), играющий важную роль в атомной и ядерной физике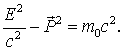

     



     В случае изолированной физической системы эта величина сохраняется не только при переходе от системы отсчета I к системе II, но также сохраняется ее значение как до, так и после реакции, происходящей в физической системе.

     Рассмотрим поучительный пример: рождение электрона и позитрона при исчезновении  -кванта с участием ядра массы 

     Требуется определить пороговую (наименьшую) энергию  кванта, достаточную для протекания реакции (рис 8.1). Задачу можно решить с помощью использования двух законов сохранения: закона сохранения энергии и закона сохранения импульса (оба - в релятивистской форме) в системе I, связанной с неподвижным ядром.

Рис. 8.1. Рождение пары электрон-позитрон вблизи массивного ядра

     Эти уравнения таковы:

     

(8.18)

     где скорость системы трех тел (как целого) после реакции. Исключая ее, так как эта скорость нас не интересует, можно найти пороговую энергию 

     Более простой путь решения - это воспользоваться инвариантом 4-импульса, приравняв его значение до реакции в системе I значению после реакции в системе II. Здесь система I связана с центром неподвижного ядра, а система П - с центром масс неподвижных в этой системе трех тел ядро - электрон - позитрон. Поскольку ищем наименьшую энергию, считаем эти три тела неподвижными в системе II (сама система II вместе с тремя телами движется относительно системы I с некоторой постоянной скоростью, которая нас не интересует).

     До реакции в системе I, где Е - это полная сумма энергий, 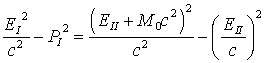- геометрическая сумма импульсов

     

.

     После реакции в системе II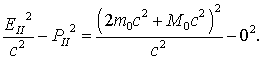

     



     Приравниваем правые части этих выражений:

     



     и получаем искомую пороговую энергия кванта

     

(8.19)

     Заметим, что без пассивного участия ядра подобная реакция невозможна. Действительно, если допустить прямое превращение 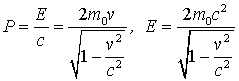кванта в пару электрон - позитрон, то законы сохранения импульса и энергии противоречат один другому

     



     (значения энергии Е не совпадают).