физика 16-30. Закону Гука где k коэффициент жёсткости системы
 Скачать 244.54 Kb. Скачать 244.54 Kb.
|
Вид преобразований при коллинеарных осях[4]Если ИСО S движется относительно ИСО S' с постоянной скоростью или, используя векторные обозначения, (последняя формула остается верной для любого направления осей координат).
Из этих преобразований следуют соотношения между скоростями движения точки и её ускорениями в обеих системах отсчета:
[править]Формула преобразования скоростейДостаточно продифференцировать Приведем более элементарный, но и более общий вывод — для случая произвольного движения начала отсчета одной системы относительно другой (при отсутствии вращения). Для такого более общего случая, можно получить формулу преобразования скоростей, например, так. Рассмотрим преобразование произвольного сдвига начала отсчета на вектор где радиус-вектор какого-то тела A в системе отсчета K обозначим за подразумевая, как всегда в классической механике, что время Тогда в любой момент времени и в частности, учитывая имеем: 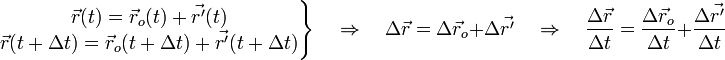 где: Если 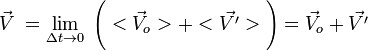 или короче — как для средних, так и для мгновенных скоростей (формула сложения скоростей). Таким образом, скорость тела относительно неподвижной системы координат равна векторной сумме скорости тела относительно движущейся системы координат и скорости системы отсчета относительно неподвижной системы отсчета. Аналогично можно получить формулу преобразования ускорений при переходе из одной системы координат в другую, верную при условии, что эти системы движутся поступательно друг относительно друга: Билет 29 Принцип относительности А. Эйнштейна: все физические явления (механические, оптические, электромагнитные и любые другие) при одинаковых начальных условиях протекают одинаково во всех инерциальных системах отсчета (ИСО). 2. Принцип постоянства скорости света: скорость света в вакууме одинакова во всех ИСО. Принцип относительности Эйнштейна представляет собой фундаментальный физический закон, согласно которому любой процесс протекает одинаково в изолированной материальной системе, находящейся в состоянии покоя или равномерного прямолинейного движения. Иначе говоря, законы физики имеют одинаковую форму во всех инерциальных системах отсчета. В основе СТО лежат два постулата, выдвинутых Эйнштейном.
В первом постулате главное то, что время тоже относительно – такой же параметр, как и скорость, импульс и др. Второй – возводит отрицательный результат опыта Майкельсона–Морли в ранг закона природы: c = const. Специальная теория относительности представляет физическую теорию, изучающую пространственно-временные закономерности, справедливые для любых физических процессов, когда можно пренебречь действием тяготения. СТО, опираясь на более совершенные данные, раскрывает новый взгляд на свойства пространства и времени. Эти свойства необходимо учитывать при скоростях движения, близких к скорости света. В природе со скоростью света распространяются (в вакууме):
Массивные частицы могут иметь скорость, приближающуюся почти вплотную к скорости света, но всё же не достигающую её точно. Например, околосветовую скорость имеют массивные частицы, полученные наускорителе или входящие в состав космических лучей. В современной физике считается хорошо обоснованным утверждение, что причинное воздействие не может переноситься со скоростью, большей скорости света в вакууме (в том числе посредством переноса такого воздействия каким-либо физическим телом). Хотя в принципе движение каких-то объектов со скоростью, большей скорости света в вакууме, вполне возможно, однако это могут быть, с современной точки зрения, только такие объекты, которые не могут быть использованы для переноса информации с их движением (например — солнечный зайчик в принципе может двигаться по стене со скоростью большей скорости света, но никак не может быть использован для передачи информации с такой скоростью от одной точки стены к другой)[4]. (Подробнее см. Сверхсветовое движение, также соответствующий раздел данной статьи ниже). БИЛЕТ 30 Преобразованиями Лоренца в физике, в частности, в специальной теории относительности (СТО), называются преобразования, которым подвергаются пространственно-временные координаты Чтобы явно различить преобразования Лоренца со сдвигами начала отсчёта и без сдвигов, когда это необходимо, говорят о неоднородных и однородных преобразованиях Лоренца. Преобразования Лоренца без сдвигов начала отсчёта образуют группу Лоренца, со сдвигами — группу Пуанкаре, иначе называемую неоднородной группой Лоренца. С математической точки зрения преобразования Лоренца — это преобразования, сохраняющие неизменной метрику Минковского, то есть, в частности, последняя сохраняет при них простейший вид при переходе от одной инерциальной системы отсчёта к другой (другими словами преобразования Лоренца — это аналог для метрики Минковского ортогональных преобразований, осуществляющих переход от одного ортонормированного базиса к другому, то есть аналог поворота координатных осей для пространства-времени). В математике или теоретической физике преобразования Лоренца могут относиться к любой размерности пространства. Именно преобразования Лоренца, смешивающие — в отличие от преобразований Галилея — пространственные координаты и время, исторически стали основой для формирования концепции единого пространства-времени.
|
