Математические модели. Замена переменных приводит дифференциальные уравнения к виду
 Скачать 0.75 Mb. Скачать 0.75 Mb.
|
|
Модель «хищник-жертва» Вольтерра-Лотки, учитывающая насыщение хищника и конкуренцию жертвы за источники питания и жизни, имеет вид: 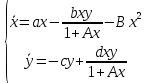 Параметр A учитывает насыщение хищника, а параметр 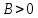 учитывает ограниченность ресурсов для размножения жертвы. учитывает ограниченность ресурсов для размножения жертвы.Замена переменных 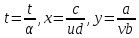 приводит дифференциальные уравнения к виду: приводит дифференциальные уравнения к виду: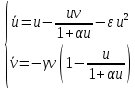 Параметр 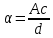 , а параметр , а параметр 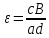 . Параметр . Параметр 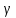 изменяет отображаемую фазовую траекторию модели, но не изменяет её фазовый портрет. изменяет отображаемую фазовую траекторию модели, но не изменяет её фазовый портрет.Точки покоя находятся из системы уравнений: 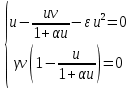 Данная система имеет три решения: 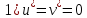 ; 2) ; 2) 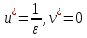 ; 3) ; 3) 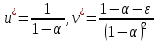 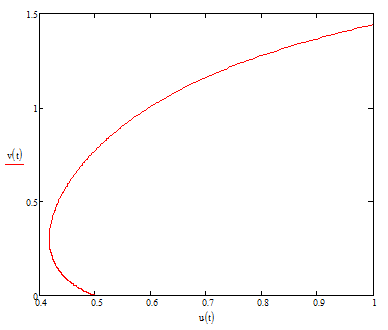 Рисунок 1 - Фазовая траектория модели На Рисунке 1 изображена фазовая траектория модели при параметрах 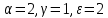 и и 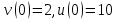 . Видно, что в данном случае хищник гибнет, а жертва остается в количестве, равном . Видно, что в данном случае хищник гибнет, а жертва остается в количестве, равном 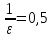 . В случае других значений параметра . В случае других значений параметра 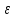 количество оставшихся жертв изменяется, продолжая выполнять равенство. Это подтверждают и графики на Рисунке 2. количество оставшихся жертв изменяется, продолжая выполнять равенство. Это подтверждают и графики на Рисунке 2.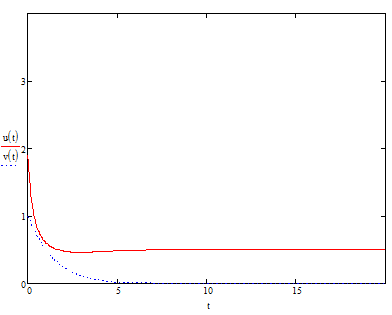 Рисунок 2 - Графики численности хищников и жертв относительно времени 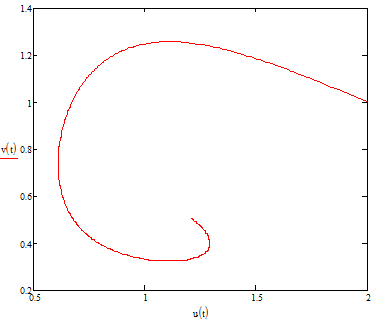 Рисунок 3 - Фазовая траектория модели На Рисунке 2 изображена фазовая траектория модели при параметрах 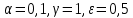 и и 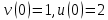 . Видно, что в данном случае хищник не погибает, достигая с жертвой равновесного сосуществования. Это подтверждают и графики на Рисунке 4. . Видно, что в данном случае хищник не погибает, достигая с жертвой равновесного сосуществования. Это подтверждают и графики на Рисунке 4.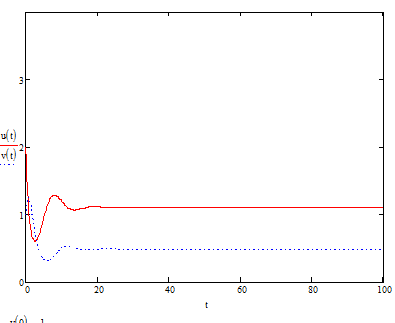 Рисунок 4 - Графики численности хищников и жертв относительно времени 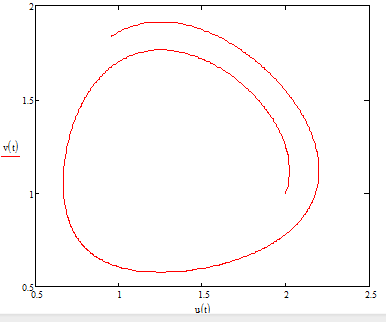 Рисунок 5 - Фазовая траектория модели На Рисунке 3 изображена фазовая траектория модели при параметрах 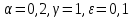 и и 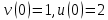 . В данном случае равновесное сосуществование хищника и жертвы нарушается, вместо этого приобретая автоколебательный характер. Это подтверждают и графики на Рисунке 6. . В данном случае равновесное сосуществование хищника и жертвы нарушается, вместо этого приобретая автоколебательный характер. Это подтверждают и графики на Рисунке 6.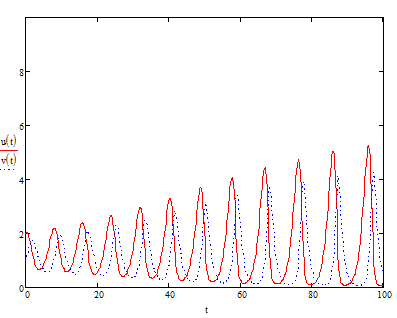 Рисунок 6 - Графики численности хищников и жертв относительно времени Линеаризация в окрестности точек покоя: 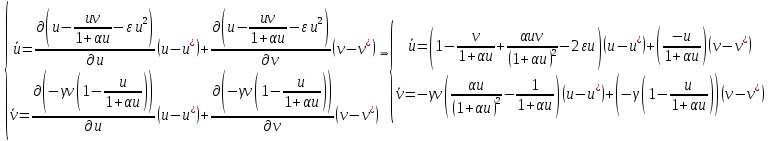 Характеристическое уравнение данной модели имеет вид: 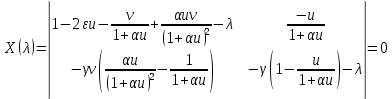 Для точки покоя 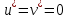 оно приобретает вид: оно приобретает вид: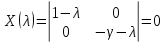 Корнями в данном случае являются 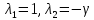 . . Для точки покоя 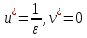 оно приобретает вид: оно приобретает вид: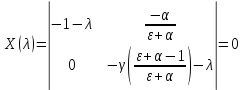 Корнями в данном случае являются 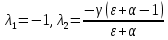 . .Корень 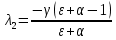 может менять знак при изменении параметров может менять знак при изменении параметров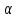 и и 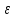 , что влияет на тип особой точки. Для определения граничных значений , что влияет на тип особой точки. Для определения граничных значений 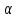 и и 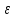 нужно решить уравнение нужно решить уравнение 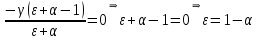 . При . При 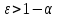 корень корень 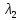 имеет отрицательный знак, а при имеет отрицательный знак, а при 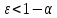 – положительный. – положительный.Для точки покоя 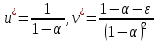 оно приобретает вид: оно приобретает вид: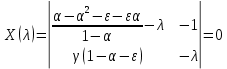 Корнями в данном случае являются 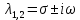 , где , где 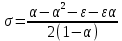 . .Действительная часть корней может менять свой знак при различных значениях 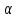 и и 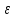 , что влияет на тип особой точки. , что влияет на тип особой точки. 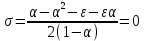 при при 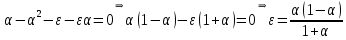 . При . При 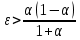 , , 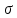 приобретает отрицательный знак, а при приобретает отрицательный знак, а при 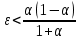 – положительный. – положительный. После уточнения фазовых траекторий модели при различных значениях параметров 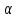 и и 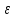 становится ясно, что модель изменяет свое поведение при пересечении прямой становится ясно, что модель изменяет свое поведение при пересечении прямой 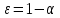 и при пересечении кривой и при пересечении кривой 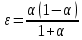 . . 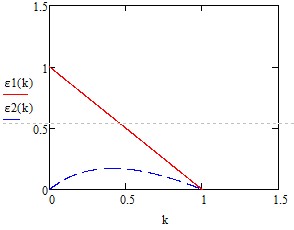 Рисунок 7 - Параметрический портрет модели Критерий Бендиксона отсутствия предельных циклов: 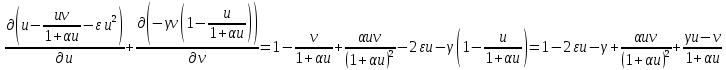 нарушается только в окрестности кривой нарушается только в окрестности кривой 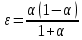 , что указывает на наличие в этой окрестности предельного цикла. , что указывает на наличие в этой окрестности предельного цикла.В соответствии с теорией бифуркаций, при переходе из равновесной зоны в автоколебательную должно рождаться либо устойчивое периодическое движение от третьего состояния равновесия, либо неустойчивое периодическое движение должно исчезать, влипая в него. 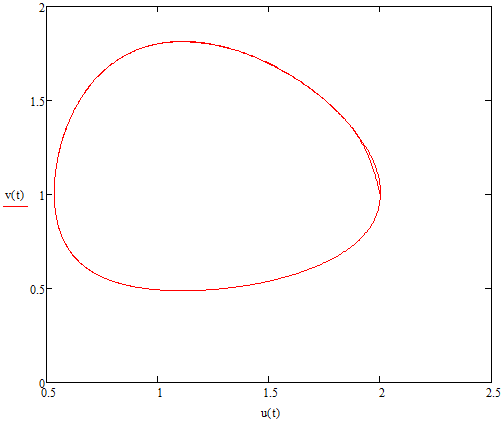 Рисунок 8 - Фазовая траектория модели 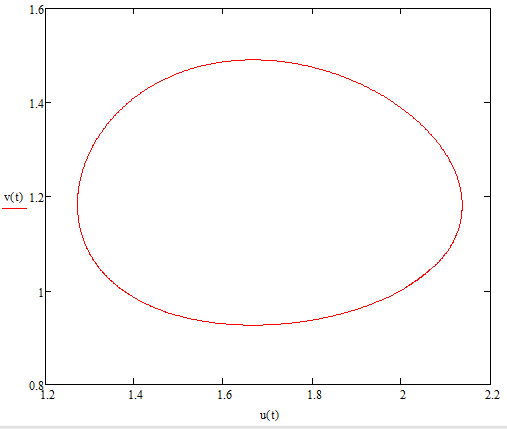 Рисунок 9 - Фазовая траектория модели На Рисунках 8 и 9 отображены фазовые траектории нелинеаризованной модели при значениях 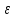 и и 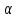 , соответствующих графику граничной кривой , соответствующих графику граничной кривой 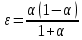 . Как видно, при этих значениях рождается устойчивое периодическое движение от третьего состояния равновесия. . Как видно, при этих значениях рождается устойчивое периодическое движение от третьего состояния равновесия.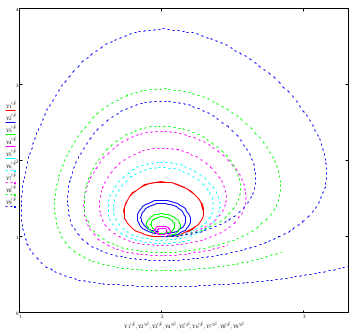 Рисунок 10 - Фазовый портрет модели На Рисунке 10 изображен фазовый портрет модели при параметрах 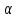 и и 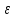 приближающихся к граничной кривой приближающихся к граничной кривой  . Предельным циклом выступает траектория Y1. Как видно, все фазовые траектории с течением времени удаляются от предельного цикла. Такое поведение соответствует неустойчивому предельному циклу. . Предельным циклом выступает траектория Y1. Как видно, все фазовые траектории с течением времени удаляются от предельного цикла. Такое поведение соответствует неустойчивому предельному циклу.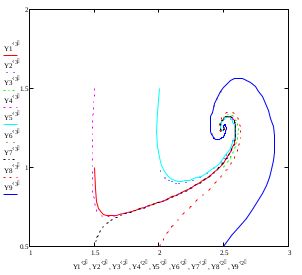 Рисунок 11 - Фазовый портрет системы первого приближения На Рисунке 11 изображен фазовый портрет линеаризованной модели при 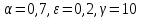 для точки покоя для точки покоя 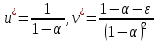 . Как видно, фазовый портрет соответствует точке покоя типа «устойчивый фокус». . Как видно, фазовый портрет соответствует точке покоя типа «устойчивый фокус».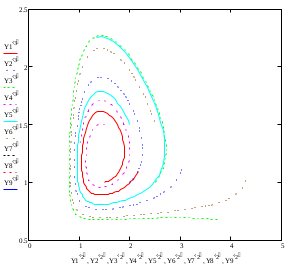 Рисунок 12 - Фазовый портрет системы первого приближения На Рисунке 12 изображен фазовый портрет линеаризованной модели при 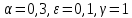 для точки покоя для точки покоя 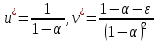 . Как видно, фазовый портрет соответствует точке покоя типа «неустойчивый фокус». . Как видно, фазовый портрет соответствует точке покоя типа «неустойчивый фокус».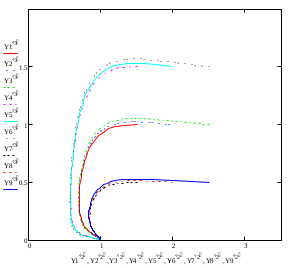 Рисунок 13 - Фазовый портрет системы первого приближения На Рисунке 13 изображен фазовый портрет линеаризованной модели при 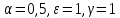 для точки покоя для точки покоя 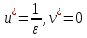 . Как видно, фазовый портрет соответствует точке покоя типа «устойчивый узел». . Как видно, фазовый портрет соответствует точке покоя типа «устойчивый узел».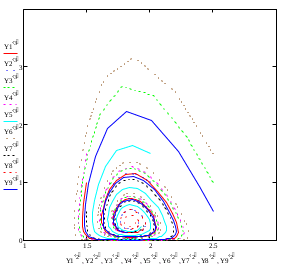 Рисунок 14 - Фазовый портрет системы первого приближения На Рисунке 14 изображен фазовый портрет линеаризованной модели при 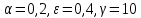 для точки покоя для точки покоя 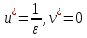 . Как видно, фазовый портрет в окрестности точки покоя соответствует точке покоя типа «седло». . Как видно, фазовый портрет в окрестности точки покоя соответствует точке покоя типа «седло».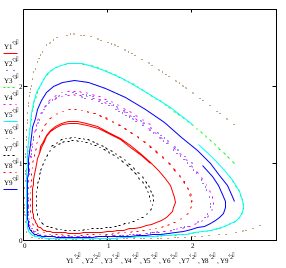 Рисунок 15 - Фазовый портрет системы первого приближения На Рисунке 15 изображен фазовый портрет линеаризованной модели при 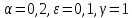 для точки покоя для точки покоя 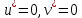 . Как видно, фазовый портрет в окрестности точки покоя соответствует точке покоя типа «седло». . Как видно, фазовый портрет в окрестности точки покоя соответствует точке покоя типа «седло».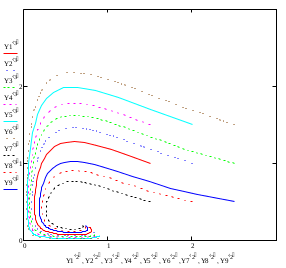 Рисунок 16 - Фазовый портрет системы первого приближения На Рисунке 16 изображен фазовый портрет линеаризованной модели при 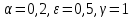 для точки покоя для точки покоя 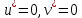 . Как видно, фазовый портрет в окрестности точки покоя соответствует точке покоя типа «седло». . Как видно, фазовый портрет в окрестности точки покоя соответствует точке покоя типа «седло».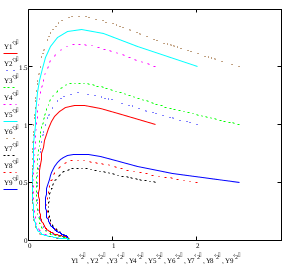 Рисунок 17 - Фазовый портрет системы первого приближения На Рисунке 17 изображен фазовый портрет линеаризованной модели при 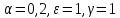 для точки покоя для точки покоя 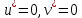 . Видно, что в данном случае хищник гибнет, а жертва остается в количестве, равном . Видно, что в данном случае хищник гибнет, а жертва остается в количестве, равном 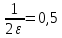 . В случае других значений параметра . В случае других значений параметра 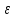 количество оставшихся жертв изменяется, продолжая выполнять равенство. Фазовый портрет в окрестности точки покоя соответствует точке покоя типа «седло». количество оставшихся жертв изменяется, продолжая выполнять равенство. Фазовый портрет в окрестности точки покоя соответствует точке покоя типа «седло». |
