Занятие 10 Обработка результатов прямых многократных измерений при боль
 Скачать 77.89 Kb.
|
2= (100,06 + 100,62) / 2 = 100,06 А . n Определяем точечную оценку дисперсии(второго центрального момента выборки 2 ): 2 S2 Xii 1 X2 m X X N , (12) n1 j j j 1 Для нашего случая, пользуясь таблицей 12, имеем S2 = (–2,94)2 0,05 + (–1,94)2 0,13 + (–0,94)2 0,19 + 0,062 0,29 + 1,062 0,17 + + 2,062 0,14 + 3,062 0,03 = 2,5 А2. 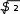 Так как дисперсия имеет квадратичную размерность для большей нагляд- ности пользуются среднимквадратическимотклонением(СКО), точечная оценка которого определяется по формулеВ нашем случае S . (13) S= 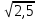 = 1, 581 А.Точечная оценка СКО среднего арифметического значения определяется по выражению Для нашего случая: (14) S S Х Х 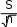 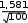 0,1581 А. Далее определяем третийцентральныймоментвыборки: 3 n 1 n m 3 3 i 1 Xi X j 1 Xj X Nj. (15) Для нашего случая, пользуясь таблицей 3, имеем: 3 = (–2,94)3 0,05 + (–1,94)3 0,13 + (–0,94)3 0,19 + 0,063 0,29 + 1,063 0,17 + + 2,063 0,14 + 3,063 0,03 = 0,060 А3. Третий центральный момент характеризует асимметрию, т.е. скошен- ность распределения, когда один спад крутой, а другой – пологий. Для симмет- ричных относительно центра распределений он равен (для выборки – близок) нулю. Для относительной характеристики асимметрии используют безразмер- ный коэффициентасимметрии: Для нашего случая 3 3 3 3 . (16) S3 3=0,060 / 1,5813 = 0,0173. Четвертыйцентральныймоментвыборки характеризует остро- или плосковершинность кривой распределения: 4 1 n X X4 m X X4 N j. (17) i j ni1 j1 Для нашего случая, пользуясь таблицей 12, находим 4 = (–2,94)4 0,05 + (–1,94)4 0,13 + (–0,94)4 0,19 + 0,064 0,29 + 1,064 0,17 + + 2,064 0,14 + 3,064 0,03 = 12,547 А4. Относительное значение четвертого центрального момента называется коэффициентомэксцесса и определяется по формуле 4 4 4 3 4 S4 3 . (18) |