Занятие 10 Обработка результатов прямых многократных измерений при боль
 Скачать 77.89 Kb. Скачать 77.89 Kb.
|
44 4 . (19) S4 В нашем случае 4 =12,547 / 1,5814 – 3 = –0,643 = 12,547 / 1,5814 = 3,67. Эксцесс распределения может иметь значения от 1 до ∞. Коэффициент эксцесса для менее протяженных распределений (треугольного, равномерного, арксинусоидального) – отрицателен (от – 2 до 0), а для более протяженных, чем нормальное, – положителен (от 0 до ∞). Для классификации распределений по их форме удобнее использовать другую функцию от эксцесса – контрэксцесс: Для нашего случая kэ =1/ kэ = 1/ 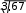 . (20)  = 0,52. = 0,52.Контрэксцесс изменяется для любых распределений лишь в пределах от 0 до 1. Таким образом, получены все основные характеристики эмпирического распределения погрешности измерения. Проверка результатов измерений на наличие грубых погрешностейПроверяем аномальность результатов наблюдений (наличие выпадающих точек). Для этого берем крайние точки выборки и определяются отношения: U1 X X1 ; S Un Xn X. (21) S Результаты сравниваем с величиной в нашем случае, для единого объема выборки n = 100 и принятой вероятности = 1 – Р = 0,05, принимаем h = 3,28. Если U h , точку исключаем и проверяем следующую и т.д. По новой выборке заново проводим все расчеты по формулам (31)...(50). Для нашего случая U1= (100 – 97,06)/1,581 = 2,7 < h= 3,28; U100=(103,06 – 100) / 1,581 = 2,3 <h=3,28, т.е. все точки приняты. Подбор теоретического закона распределенияПостроение эмпирического распределения погрешности Для нашего примера, по данным таблицы 3, построим гистограмму и по- лигон для наглядного представления формы закона распределения погрешно- стей (рис. 1). По оси абсцисс в масштабе откладываем m классов в размерности изме- ряемой величины: 7 классов через 1 Н. По оси ординат откладываем частоты, причем за максимальное значение принимаем немного большее целое значение, чем наибольшая частота. Для нашего примера njmax = n4= 27, поэтому по оси ординат будем откладывать цифры от 0 до 30. Отношение масштабов между осями (с учетом правила «золотого сечения») равно njmax / R 5/8, т.е. длина наибольшей ординаты в 5/8 раза короче глины наибольшей абсциссы. Гистограмму строят так. Над каждым классом (интервалом) по оси абс- цисс строят прямоугольник (площадь которого пропорциональна частоте Nj) и отсекают его по оси ординат в соответствии с частотой в этом классе nj(рис. 1). Гистограмму можно расположить симметрично, т.е. перенести некоторое число отсчетов из данного столбца в симметричный с ним столбец. Это упро- щает расчеты в 1,5…2 раза. Именно поэтому m будет нечетным, т.е. центром симметрии является центральный столбец. Полигон – есть ломаная линия, построенная по точкам середин классов. Концы полигона или отсекают по Хminи Хmax, или соединяют с осью абсцисс в серединах положения (от нуля и m+ 1) классов (рис. 1). Идентификация закона распределения методом моментов Имея значения kэ, и вид эмпирического распределения (рис. 1), можно подобрать теоретический закон распределения. Для этого пользуются таблицей 4. 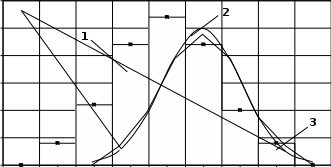 nj 30 nj 3025 20 15 10 5 0 97,06 98,06 99,06 100,06 101,06 102,06 103,06 Х, А Рис. 1. Распределениепогрешностей: 1 – гистограмма эмпирического распределения; 2 – полигон эмпирического рас-пределения;3–теоретическаякриваяраспределения Таблица 4 Значения асимметрии, эксцесса и контрэксцессадлязаконовраспределения
В нашем случае при kэ= 0,62, = 2,57 подходит как нормальное, так и распределение Симпсона. Более точную оценку может дать только использова- ние критериев согласия. Идентификация закона распределения при помощи критерия согласия Существует три основных критерия согласия: 2 (омега квадрат) Мизеса–Смирнова – мощный критерий, но сложный в расчетах; 2 (хи квадрат) Пирсона – достаточно достоверный при n> 50 и m> 5; D(ди) Колмогорова–Смирнова – быстрая, но не очень точная оценка при n > 35. В дальнейшем будем использовать критерий 2. С целью определения дифференциальной функции распределения и сравнения ее с эмпирическим распределением для экспоненциальных законов определяем сначала квантиль tдля каждого класса и заносим в таблицу 3 tj Xj XS . (22) Далее определяем теоретическую дифференциальную функцию распре- деления для каждого класса по формуле нормальное распределение 1t2 j распределение Лапласа Р*t 1 e 2 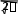 j ; (23) j 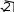 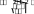 Р*t e Р*t e 2 . (24) Дифференциальную функцию, вычисленную по формулам (23) и (24) для экспоненциальных распределений, необходимо привести к выборке, поэтому определим для всех классов и заполним таблицу 3: Рj ( X ) Р* (t) d j j j S . (25) Для закона распределения Симпсона 0 при Хi Х1; i 1 4Х Х Х Х Р(Х) = Х Х 2 2 1 при Х1 < Хi< 2 1 ; 2 (26) 4 Х2 Х1 Х Х 2 1 X X2 при 2 1 2 < Хi< Х2; 0 при Хi Х2. За Х1 и Х2 примем точки пересечения с осью абсцисс полигона, т.е. Х1 = 96,02 Н; Х2 = 104,02 Н. Вместо Х подставим поочередно Хjв функцию Р(Х) и определим Pj(Xj), заполним строку таблицы 3. После расчета функции Pj(Xj) для всех законов распределения определяем теоретическую частоту для всех классов и заполняем таблицу 3: j j j Ε PXn. (27) Определяем величину 2: m 2 E j 1 j nj 2 nj . (28) Для удобства расчета поэлементно сводим всё в таблицу 3. Находим, что для нормального распределения 2 = 0,608, распределения Лапласа 2 = 38,756, а для распределения Симпсона 2 = 10,545. Чем меньше 2, тем больше подхо- дит распределение. Далее определяем число степеней свободы эмпирического ряда: = m–1 –r, (29) где r – число определенных по выборке параметров, необходимых для совме- щения гистограммы и теоретического распределения. Для экспоненциальных распределений это X и S (т.е. r = 2), для тре- угольного и равномерного X, (т.е. r= 2). Тогда в нашем примере = 7 – 3 = 4. По таблице П 5 (приложение), в соответствии с значением , определяем строку и по строке смотрим, какая из цифр наиболее близка к значению 2 , определяем столбец и вероятность согласия эмпирического и теоретического распределений. Таким образом, вероятность согласия для нормального закона распределения Р 0,95; Лапласа P = 0; Симпсона P = 0. Наиболее подходящим из анализируемых распределений является нормальное распределение (ЗНР), поэтому именно его (Еj) наносим на рисунок 1. Определение погрешности измеренийСначала определяют границы доверительного интервала случайной по-грешности измерений: где tР–квантиль распределения. Р tРSX, (30) Для нормального распределения, если n> 30 при Р=0,9 t0,9 = 1,64, при Р= 0,95 t0,95 = 1,96, при Р=0,99 t0,99 = 2,58. Для распределения Лапласа при Р =0,99 t0,9 = 1,38, при Р=0,95 t0,95= 1,87. Для распределения Симпсона – 2,4SХ. В нашем примере 0,95 1,96 0,1581 0,5748А. Далее определяем доверительныеграницынеисключеннойсистематиче-скойпогрешности. В качестве границ неисключенной систематической погрешности прини- маем погрешности изготовления меры = ± 0,9 А. Доверительные границы суммарнойпогрешностирезультатаизмерения Х зависят от соотношения S: S Х если < 0,8, то границы погрешности результата измерения прини- маются равными случайной погрешности, Σ = ; Х если S > 8, то границы погрешности результата измерения принима- ются равными систематической погрешности, Σ = ; Х если 0,8 S 8, то общую погрешность измерения определяют по формуле Σ = K S, (31) где К– коэффициент, зависящий от соотношения марного СКО результата измерений; и ; S – оценка сум- S 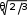 KΔθ ; (32) KΔθ ; (32) X 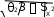 S S . (33) Х Для нашего примера S= 0,9 / 0,1581 = 5,69, тогда  К= (0,2771 + 0,9) / (0,1581 + 0,9 2/3) = 2,63; К= (0,2771 + 0,9) / (0,1581 + 0,9 2/3) = 2,63;S = 0,35 А; Σ = 2,63 ∙ 0,35 = 1,84 А. Результат измерения записываем в виде Q= Х Σ, при Р= …, n =.. (34) А= (100,0 1,8) Н, при Р= 0,95 %; n = 100. Определение числа измерений для частичного и полного исключения случайной погрешностиS Х При использовании однократного наблюдения (n= 1) = 1,42 А, тогда Х S= 0,9/1,414 = 0,63, т.е. на результат однократного измерения оказывает влияние случайная погрешность деляем следующим образом: для частичного исключения . Число измерений для исключения 0,8S 2 опре- |
