расчет ЦАП. ПЗ 6 Расчет ЦАП и АЦП. Занятие 6 Расчет параметров цифроаналоговых и аналогоцифровых преобразователей
 Скачать 0.73 Mb. Скачать 0.73 Mb.
|
|
Практическое занятие 6 Расчет параметров цифроаналоговых и аналогоцифровых преобразователей Цель занятия: Закрепить теоретические знания по теме занятия. Приобрести навыки сравнительного анализа схем преобразователей информации. Совершенствовать практические навыки моделирования работы ЦАП и АЦП. Совершенствовать навыки практической работы на ПК. Техническое и программное обеспечение: персональный компьютер с операционной системой WindowsXP, пакет MS Office. 6.1. Краткие теоретические сведения Аналогово-цифровой преобразователь (АЦП) — один из самых важных электронных компонентов в измерительном и тестовом оборудовании. АЦП преобразует напряжение (аналоговый сигнал) в код, над которым микропроцессор и программное обеспечение выполняют определенные действия. Существует несколько основных типов архитектуры АЦП, хотя в пределах каждого типа существует также множество вариаций. Различные типы измерительного оборудования используют различные типы АЦП. Например, в цифровом осциллографе используется высокая частота дискретизации, но не требуется высокое разрешение. В цифровых мультиметрах нужно большее разрешение, но можно пожертвовать скоростью измерения. Системы сбора данных общего назначения по скорости дискретизации и разрешающей способности обычно занимают место между осциллографами и цифровыми мультиметрами. В оборудовании такого типа используются АЦП последовательного приближения либо сигма-дельта АЦП. Существуют также параллельные АЦП для приложений, требующих скоростной обработки аналоговых сигналов, и интегрирующие АЦП с высокими разрешением и помехоподавлением. 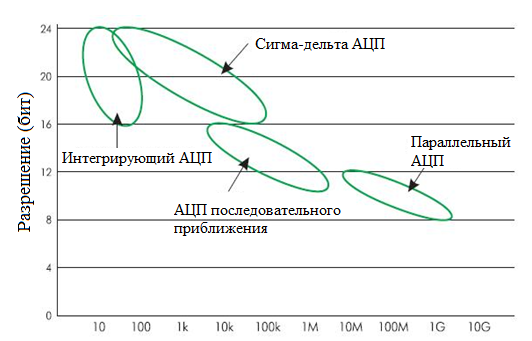 Рис. 6.1. Типы АЦП - разрешение в зависимости от частоты дискретизации На рис. 6.1 показаны возможности основных архитектур АЦП в зависимости от разрешения и частоты дискретизации. Существуют различные типы АЦП. Мы остановимся лишь на тех типах, которые получили в настоящее время наибольшее распространение. 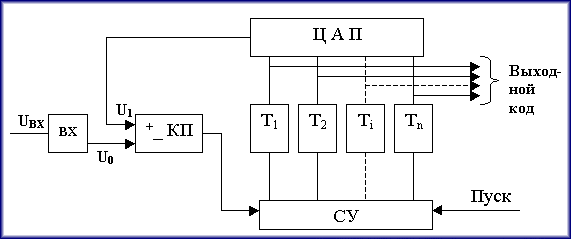 Рис. 6.2. Схема АЦП последовательного приближения АЦП последовательного приближения (АЦППП). Структурная схема АЦППП приведена на рисунке 6.2. Схема работает следующим образом. Входной аналоговый сигнал Uвх перед началом преобразования запоминается схемой выборки – хранения ВХ, что необходимо, так как в процессе преобразования необходимо изменение аналогового сигнала. Далее по команде “Пуск” с помощью сдвигового регистра последовательно во времени каждый триггер Ti, начиная со старшего разряда, переводит в положение 1 соответствующий разряд ЦАП. Напряжение U1 (или ток) с выхода ЦАП сравнивается с входным аналоговым сигналом с помощью компаратора КП. Если U0 > U1, на выходе компаратора сохраняется низкий уровень и в триггере сохраняется единица, при U0 < U1 срабатывает компаратор и переводит триггер в положение 0. После окончания цикла на выходах триггеров получается двоичный код, соответствующий (при идеальных элементах) U0 с точностью до половины младшего разряда. Погрешность АЦППП определяется неточностью ЦАП, зоной нечувствительности и смещением нуля компаратора, а также погрешностью схемы выборки – хранения.Поскольку в такой схеме ошибка в каком – либо разряде в дальнейшем не корректируется, необходимо, чтобы время на “взвешивание” каждого разряда было достаточно для затухания переходного процесса до уровня, соответствующего половине младшего разряда, и чтобы при разбалансе U1 – U0 на это значение компаратора успел сработать. Общее время преобразования tпр=tвх+n(tз,к+tу+tц)+tcб, где tвх – время, необходимое для фиксации Uвх схемой ВХ; n – число разрядов; tз,к – время задержки, вносимое компаратором; tу – время установления U1 на входе ЦАП; tц – время задержки цифровых элементов в схеме управления и срабатывания триггера; tсб – время, необходимое для сброса ЦАП в исходное состояние, включая время, необходимое для синхронизации с началом такта.Наибольшую долю в tпр обычно вносит tу, наибольшая величина которого может быть оценена следующим образом: tу=(1+n)Тэln2, где Tэ – эквивалентная постоянная времени на входе ЦАП. Если на его выходе включен ОУ, который полезен для уменьшения выходного сопротивления и ускорения тем самым переходного процесса, то Tэ» 1/2p fср (fср – частота среза ОУ по контуру обратной свази). При 12 – разрядном АЦП и использовании быстродействующего ЦАП с tу=100 нс время tпр близко к 1,5 мкс. В большинстве случаев tпр такого преобразователя достигает 10…100 мкс. АЦП параллельного типа (АЦПП). Существенное уменьшение tпр удается получить в АЦП параллельного типа. Его структурная схема приведена на рис.6.3. 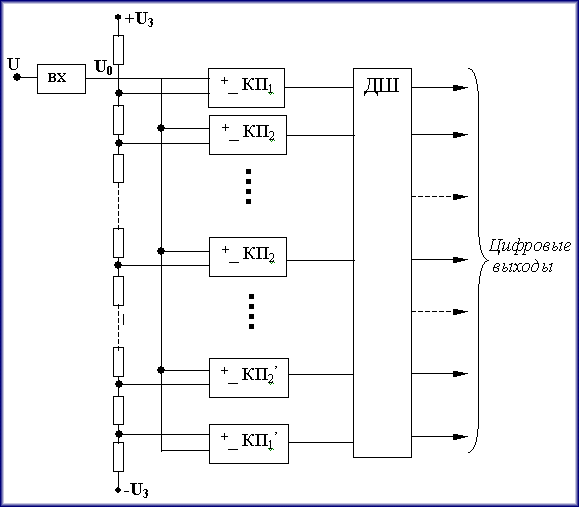 Рис. 6.3. Схема АЦП параллельного типа Здесь входная аналоговая величина U0 с выхода схемы ВХ сравнивается с помощью 2n+1 – 1 компараторов с 2(2n-1) эталонными уровнями, образованными делителями из резисторов равного сопротивления. При этом срабатывают m младших компараторов, образующих на выходах схем И-НЕ нормальный единичный код, затем который с помощью специального дешифратора ДШ преобразуется в двоичный выходной сигнал. Погрешность АЦПП определяется неточностью и нестабильностью эталонного напряжения, резистивного делителя и погрешностями компараторов. Значительную роль могут играть входные токи компараторов, если делитель недостаточно низкоомный. Время преобразования складывается из следующих составляющих: tпр = tвх + tз,к + a tл,сi , где tл,сi – Время задержки логичесих схем; k – число последовательно включенных логических схем. При использовании компаратров со стробированием АЦПП может быть без схемы ВХ. При этом он обеспечивает наибольшее быстродействие по сравнению с любыми другими АЦП. Дискретизация, квантование, кодирование. Аналоговый сигнал является непрерывной функцией времени, в АЦП он преобразуется в последовательность цифровых значений. Сам процесс преобразования включает в себя три основные операции: дискретизацию, квантование и кодирование (рис. 6.4). Операция дискретизации состоит в том, что по заданному аналоговому сигналу S(t) (рис. 6.4, a) строится дискретный сигнал S(nT), причем S(nT) =S(t). Физически такая операция эквивалентна мгновенной фиксации выборки из непрерывного сигнала S(t) в моменты времени t = nТ, после чего образуется последовательность выборочных значений {(S(nT)}. Конечно, такую дискретизацию на практике осуществить невозможно. Реальные устройства, запоминающие значения аналогового сигнала (они называются устройства выборки и хранения - УВХ), не в состоянии сделать этого мгновенно- время подключения их к источнику сигнала всегда конечно. Кроме того, из-за не идеальности ключей и цепей заряда запоминающей емкости УВХ, значение взятой выборки S(nT) в той или иной степени отличается от величины исходного сигнала S(t). Тем не менее в абстрактных рассуждениях равенство S(t) = S(nT) считается справедливым. Поскольку дискретный сигнал S(nT) в моменты времени t = nТ сохраняет информацию об аналоговом сигнале S(t) и в спектре сигнала S(nT) содержится спектр сигнала S(t), то последний, очевидно, может быть восстановлен. Для этого дискретный сигнал достаточно пропустить через фильтр низких частот, полоса которого соответствует полосе частот исходного сигнала. Условие, при котором восстановление исходного сигнала S(t) по его дискретным значениям S(nT) будет возможным, сформулировано в известной теореме Котельникова (теорема отсчетов): «Если наивысшая частота в спектре функции S(t) меньше, fmax, то функция S(t) полностью определяется последовательностью своих значений в моменты, отстоящие друг от друга не более, чем на l/fmax секунд. Другими словами, чтобы восстановление было точным, частота дискретизации F должна по меньшей мере в два раза превышать максимальную частоту fmax в спектре преобразуемого аналогового сигнала S(t). Эта предельно допустимая максимальная частота fmax в спектре сигнала называется частотой Найквиста fн. Нередко частоту Найквиста fн путают со скоростью Найквиста Fн, которая характеризует минимально возможную для данной частоты Найквиста скорость дискретизации аналогового сигнала и которая вдвое выше максимальной частоты в его спектре (частоты Найквиста). На практике при дискретизации широкополосных сигналов приходится жестко ограничивать их спектры с помощью высокодобротных фильтров низких частот, которые называются анти-элайсинг фильтрами. Спад характеристики у таких фильтров (как, впрочем, и у любых других фильтров) не бывает строго вертикальным. 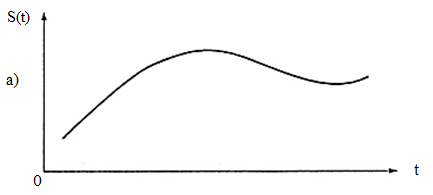 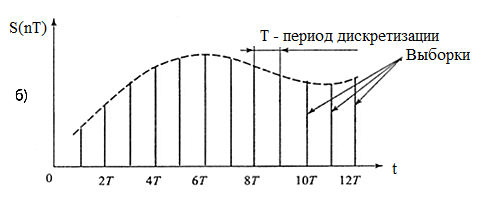 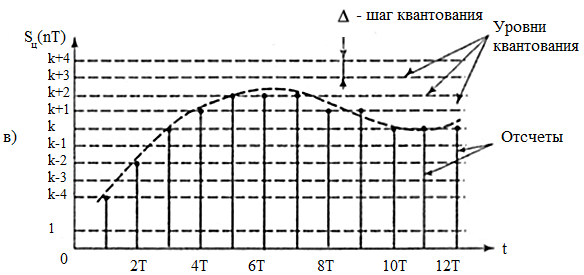 Рис. 6. 4. Аналого-цифровое преобразование: (а) – исходный аналоговый сигнал; (б) - дискретизация; (в) – квантование Поэтому реально частота fmax должна быть несколько ниже частоты Найквиста fH. Тем не менее при анализе теоретических моделей аналого- цифровых преобразователей часто пользуются понятиями частоты и скорости Найквиста, полагая, что скорость Найквиста FH - это удвоенная частота Найквиста fH, т.е. FH = 2fH В подавляющем большинстве случаев используется равномерная (с постоянным периодом) дискретизация — как по причине того, что к ней легче применить математический аппарат, так и по причине того, что устройства для ее осуществления гораздо проще реализовать физически. После того, как сигнал дискретизирован, производится его квантование и кодирование, что, собственно, и является основной операцией при аналого-цифровом преобразовании. На этом этапе по заданному дискретному сигналу S(nT) строится цифровой кодированный сигнал Sц(nT). Также, как и дискретный, цифровой сигнал описывается решетчатой функцией, но в данном случае эта решетчатая функция является еще и квантованной, т.е. способной принимать лишь ряд дискретных значений, которые называются уровнями квантования (рис. 6.4, в). Уровни квантования образуются путем разбиения всего диапазона, в котором изменяется аналоговый сигнал, на ряд участков, каждому из которых присваивается определённый номер. Эти номера кодируются заранее выбранным кодом, чаще всего двоичным, а их число N выбирается равным 2m, где m - разрядность кода. Если сигнал однополярный, то все 2m уровней будут выражать положительные значения аналогового сигнала. Для двухполярного одна половина (2m/2=2m-1) уровней будет выражать отрицательные значения сигнала, другая (также 2m-1) - положительные. Квантование может осуществляться двумя способами. При одном способе расстояние между любыми двумя соседними уровнями, которое называется шагом квантования, будет одинаковым, (так называемое линейное квантование). Способ, когда шаг квантования изменяется, - это нелинейное квантование. В дальнейшем будут рассмотрены линейные АЦП. Дискретные сигналы, как и аналоговые, образуют линейное пространство относительно операций сложения, вычитания, умножения, если выполняется условие теоремы Котельникова. Цифровые же сигналы, полученные путем квантования, линейного пространства относительно операций сложения и умножения не образуют. Во-первых, процедура квантования почти всегда сопровождается появлением неустранимой погрешности. Во-вторых, линейная комбинация цифровых сигналов, выражаемых m-разрядными кодами, может иметь разрядность большую, чем m (особенно при операциях умножения), чтобы получить m-разрядный код результата, приходится выполнять операцию округления и усечения. Поэтому устройства цифровой обработки сигналов, реализующие преобразование одной цифровой последовательности Sц1(nT) в другую Sц2(nТ) путем выполнения обычных арифметических операций сложения и умножения (в САУ обычно расчет регуляторов), являются, в принципе, нелинейными. Часто при проектировании систем, включающих в себя устройства аналого-цифрового и цифро-аналогового преобразований сигналов, полученных в результате ограничения спектра широкополосных сигналов с помощью фильтров низких частот, разработчики переносят утверждение теоремы Котельникова о возможности точного восстановления исходного аналогового сигнала по отсчетам дискретного на результат аналого-цифрового и цифро-аналогового преобразований, что является в принципе, ошибочным. Поэтому в том виде, в котором теорема Котельникова сформулирована для дискретных сигналов, к системам, включающим в себя АЦ- и ЦА- преобразования, неприменима, она может служить только теоретической моделью для очень приблизительных расчетов. Поскольку реальные АЦП не могут произвести аналого-цифровое преобразование мгновенно, входное аналоговое значение должно удерживаться постоянным, по крайней мере от начала до конца процесса преобразования (этот интервал называют временем преобразования). В настоящее время выпускается большее число интегральных АЦП, которые отличаются конструктивной и функциональной закономерностью, но в основу работы заложены некоторые стандартные, фундаментальные принципы. При этом в структуре некоторых АЦП присутствует устройство УВХ, в других отсутствует. Разрядность АЦП. Разрядность АЦП характеризует количество дискретных значений, которые преобразователь может выдать на выходе. В двоичных АЦП разрядность измеряется в битах. Разрядностью АЦП определяется и его разрешение- минимальное изменение величины входного аналогового сигнала, которое может быть зафиксировано данным АЦП. АЦП преобразовывает сигнал (напряжение), находящийся в диапазоне измеряемых сигналов. Нижняя и верхняя граница этого диапазона определяются напряжениями, поданными на соответствующие выводы. Для микроконтроллера (МК) со встроенным АЦП, нижняя граница - это уровень GND (0 В), а верхняя - подается на отдельный вывод (AREF- Analog Reference) или используются внутренние источники опорных напряжений. При диапазоне входных напряжений от 0 В до 5 В и использовании 10-битного АЦП мы имеем следующее разрешение АЦП (см. рис. 6.5). Т. е. АЦП в состоянии различить сигналы, которые отличаются на 4,9 мВ. При увеличении сигнала на 4,9 мВ - результат преобразования увеличится на 1. Если для такого же диапазона входных сигналов использовать АЦП с большей разрядностью, то можно зафиксировать меньшие значения, т.е. получить более точное значение сигнала (на рис. 6.6 представлены значения при использовании 24-битного АЦП). При отсутствии различного рода ошибок, разрядность АЦП определяет теоретически возможную точность АЦП. На практике разрешение АЦП ограничено отношением сигнал/шум входного сигнала. При большой интенсивности шумов на входе АЦП различение соседних уровней входного сигнала становится невозможным, то есть ухудшается разрешение. При этом реально достижимое разрешение описывается эффективной разрядностью (Effective Number Of Bits- ENOB), которая меньше, чем реальная разрядность АЦП. При преобразовании сильно зашумлённого сигнала младшие разряды выходного кода практически бесполезны, так как содержат шум. 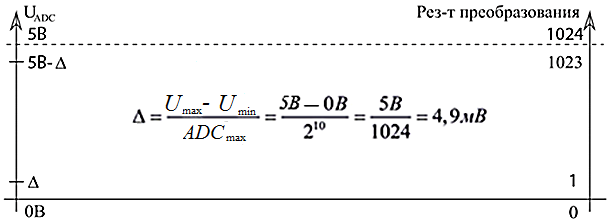 Рис. 6.5. Разрешение 10-битного АЦП 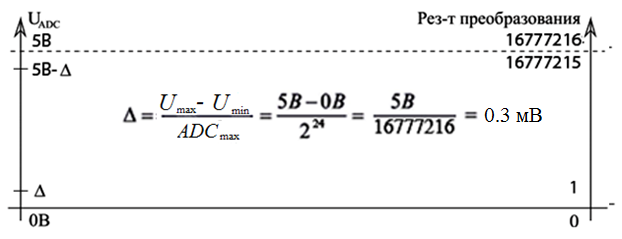 Рис. 6.6. Разрешение 24-битного АЦП Параллельные АЦП. Большинство высокоскоростных осциллографов и некоторые высокочастотные измерительные приборы используют параллельные АЦП из-за их высокой скорости преобразования, которая может достигать 5 Г (5·109) отсчетов/сек для стандартных устройств и 20 Г отсчетов/сек для оригинальных разработок. Обычно параллельные АЦП имеют разрешение до 8 разрядов, но встречаются также 10- разрядные версии. Рис. 6. 7 показывает упрощенную блок-схему 3- разрядного параллельного АЦП (для преобразователей с большим разрешением принцип работы сохраняется. Здесь используется массив компараторов, каждый из которых сравнивает входное напряжение с индивидуальным опорным напряжением. 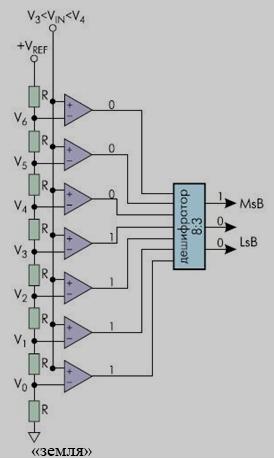 Рис. 6.7. АЦП параллельного преобразования Такое опорное напряжение для каждого компаратора формируется на встроенном прецизионном резистивном делителе. Значения опорных напряжений начинаются со значения, равного половине младшего значащего разряда (LSB), и увеличиваются при переходе к каждому следующему компаратору с шагом, равным VREF /2 (Vref- опорное напряжение). В результате для 3- разрядного АЦП требуется 23 - 1 или семь компараторов. А, например, для 8-разрядного параллельного АЦП потребуется уже 255 (или (28 - 1)) компараторов. С увеличением входного напряжения компараторы последовательно устанавливают свои выходы в логическую единицу вместо логического нуля, начиная с компаратора, отвечающего за младший значащий разряд. Можно представить преобразователь как ртутный термометр: с ростом температуры столбик ртути поднимается. На рис. 6.7 входное напряжение попадает в интервал между V3 и V4, таким образом 4 нижних компаратора имеют на выходе "1", а верхние три компаратора - "0". Дешифратор преобразует (23 - 1) - разрядное цифровое слово с выходов компараторов в двоичный 3-х разрядный код. Состояния компараторов и выходной сигнал в зависимости от уровня входного напряжения можно увидеть в табл.6.1. Таблица 6.1 Состояние компараторов и выходные сигналы АЦП
Способ параллельного кодирования обеспечивает наибольшую скорость преобразования, из-за чего его иногда называют способом «мгновенного кодирования». И действительно, время преобразования здесь — всего один такт, и ограничено оно лишь быстродействием компараторов и задержкой на шифраторе. Для того, чтобы схема могла работать с биполярным сигналом, в месте подключения "земли" (рис.6.7) подключается отрицательное опорное напряжение - Uоп. Если в состав параллельных АЦП входит большое число компараторов с разным быстродействием, то для синхронизации моментов формирования выходного кода шифратор стробируют сигналом частоты дискретизации (рис. 6.8). 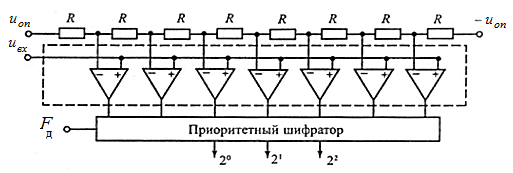 Рис. 6.8. Структурная схема параллельного биполярного АЦП с синхронизацией шифратора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
