расчет ЦАП. ПЗ 6 Расчет ЦАП и АЦП. Занятие 6 Расчет параметров цифроаналоговых и аналогоцифровых преобразователей
 Скачать 0.73 Mb. Скачать 0.73 Mb.
|
|
Двухкаскадный последовательно-параллельный АЦП. Последовательно-параллельные АЦП являются тем классом преобразователей, который позволяет использовать быстродействие и простоту параллельных АЦП для создания многоразрядных преобразователей последовательного типа с высокой разрешающей способностью. Структурная схема двухкаскадного последовательно-параллельного АЦП приведена на рис. 6.9. 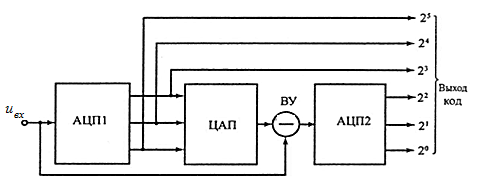 Рис. 6.9. Структурная схема 2-каскадного последовательно – параллельного АЦП Как видно из рисунка, все устройство в целом осуществляет преобразование входного аналогового сигнала Uвх с 6-разрядным разрешением. Однако преобразование осуществляется в два приема с помощью двух 3-разрядных АЦП. Оба они, и АЦП1, и АЦП2 — параллельного типа, т. е. являются однотактными. Но алгоритм работы данной схемы предполагает их последовательное действие, и общее количество тактов равно трем. В течение первого такта осуществляется грубое квантование входного сигнала Uвх с трехразрядной точностью при помощи АЦП1. Результат этого квантования подается на выход АЦП в качестве старших разрядов выходного кода (23 - 25) и одновременно поступает на вход 3- разрядного ЦАП. Во втором такте аналоговое напряжение, которое формируется на выходе ЦАП и отражает результат грубого квантования в первом такте, сравнивается с истинным значением входного сигнала Uвх. Разница, полученная на выходе вычитающего устройства ВУ, поступает на вход второго трехразрядного АЦП (АЦП2), который в третьем такте осуществляет ее преобразование в три младших разряда выходного кода (20 - 22). Таким образом, быстродействие представленного на рис. 6.7 6-разрядного АЦП в три раза ниже, чем то, которым обладал бы 6-разрядный параллельный АЦП. Но, если для создания параллельного потребовалось бы 26 – 1 = 63 компаратора, то для создания двухкаскадного последовательно-параллельного — всего 2 · (23 - 1), то есть 2 · 7 = 14 компараторов. Выигрыш — более чем в 4 раза. Количество каскадов в АЦП с подобной структурой может быть больше двух, поэтому их иногда называют многокаскадными. В этом случае на входе каждого АЦП следует размещать устройство выборки и хранения (УВХ). Несмотря на свою быстроту, параллельные АЦП имеют свои недостатки. Из-за необходимости использовать большое количество компараторов параллельные АЦП потребляют значительную мощность, и их нецелесообразно использовать в приложениях с батарейным питанием. АЦП последовательного приближения. Когда необходимо разрешение 12, 14 или 16 разрядов и не требуется высокая скорость преобразования, а определяющими факторами являются невысокая цена и низкое энергопотребление, то обычно применяют АЦП последовательного приближения. Этот тип АЦП чаще всего используется в разнообразных измерительных приборах и в системах сбора данных. В настоящий момент АЦП последовательного приближения позволяют измерять напряжение с точностью до 16 разрядов с частотой дискретизации от 1К (210) до 1М (220) отсчетов/сек. (рис. 6.10) показывает упрощенную блок-схему АЦП последовательного приближения. 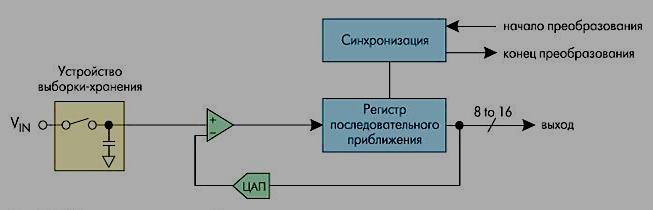 Рис. 6.10. АЦП последовательного приближения В основе АЦП данного типа лежит специальный регистр последовательного приближения. В начале цикла преобразования все выходы этого регистра устанавливаются в логический 0 за исключением первого (старшего) разряда. Это формирует на выходе внутреннего цифро-аналогового преобразователя (ЦАП) сигнал, значение которого равно половине входного диапазона АЦП. А выход компаратора переключается в состояние, определяющее разницу между сигналом на выходе ЦАП и измеряемым входным напряжением. Приближение к аналоговому сигналу происходит не "лесенкой", т.е. начиная с младшего разряда, а скачками, вначале большими ступенями, так как заполнение регистра последовательного приближения начинается со старшего разряда кода, затем ступени уменьшаются в соответствии с "весом" разряда. Дерево, иллюстрирующее работу 3-х разрядного АЦП с таким регистром, изображено на рис. 6.11. 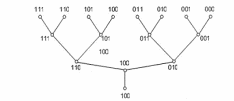 Рис. 6.11. Дерево аналого-цифрового преобразования Например, для 8-разрядного АЦП последовательного приближения (рис.6.12) выходы регистра при этом устанавливаются в "10000000". 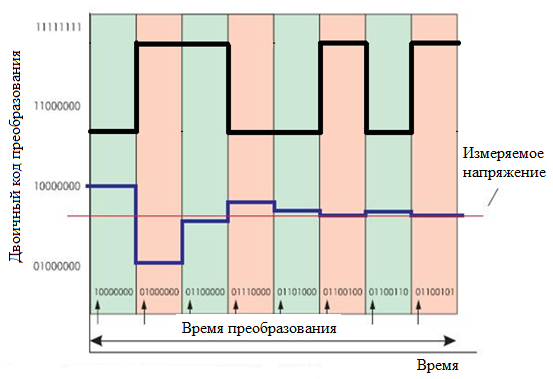 Рис. 6.12. Состояние компаратора и выходной код АЦП Если входное напряжение меньше половины входного диапазона АЦП, тогда выход компаратора примет значение логического 0. Это дает регистру последовательного приближения команду переключить свои выходы в состояние "01000000", что, соответственно, приведет к изменению выходного напряжения с ЦАП, подаваемого на компаратор. Если при этом выход компаратора по-прежнему оставался бы в "0", то выходы регистра переключились бы в состояние "00100000". Но на этом такте преобразования выходное напряжение ЦАП меньше, чем входное напряжение, и компаратор переключается в состояние логической 1 (см.рис.6.10). Это предписывает регистру последовательного приближения сохранить "1" во втором разряде и подать "1" на третий разряд. Описанный алгоритм работы затем вновь повторяется до последнего разряда. Таким образом, для АЦП последовательного приближения требуется один внутренний такт преобразования для каждого разряда, или N тактов для N-разрядного преобразования. Тем не менее, работа АЦП последовательного приближения имеет особенность, связанную с переходными процессами во внутреннем ЦАП. Теоретически, напряжение на выходе ЦАП для каждого из N внутренних тактов преобразования должно устанавливаться за одинаковый промежуток времени. Но на самом деле этот промежуток в первых тактах значительно больше, чем в последних. Поэтому время преобразования 16-разрядного АЦП последовательного приближения более, чем в два раза превышает время преобразования 8-разрядного АЦП данного типа. АЦП последовательного приближения позволяют кратчайшим путем приблизиться к измеряемой величине и завершить процесс преобразования всего за m последовательных приближений (m-разрядность выходного кода) вместо 2m-1 , которые потребовались бы в случае использования метода одностороннего приближения. Выигрыш в быстродействии будет тем большим, чем больше разрядность m. При m=6 такой выигрыш будет более чем десятикратным (6 против 26=64), то при m=10 он достигнет более двух порядков (10 против 210 = 1024). С помощью таких АЦП, в зависимости от числа используемых разрядов, можно получить до 105 - 106 преобразований в секунду. К тому же статическая погрешность преобразователей данного типа весьма незначительна и определяется в основном используемым ЦАП. Это позволяет реализовать разрешающую способность до 16 двоичных разрядов и более. Данный класс АЦП, представляя собой разумный технический компромисс между точностью и быстродействием, находит широкое применение - как при построении цифровых измерительных приборов, так и в различных системах цифровой обработки быстро меняющихся сигналов совместно с УВХ или без последних. Сигма-дельта АЦП. Для проведения большинства измерений часто не требуется АЦП со скоростью преобразования, которую даёт АЦП последовательного приближения, зато необходима большая разрешающая способность. Сигма-дельта АЦП могут обеспечивать разрешающую способность до 24 разрядов, но при этом уступают в скорости преобразования. Так, в сигма-дельта АЦП при 16 разрядах можно получить частоту дискретизации до 100 К отсчетов/сек, а при 24 разрядах эта частота падает до 100-1 К отсчетов/сек, в зависимости от устройства. Обычно сигма-дельта АЦП применяются в разнообразных системах сбора данных и в измерительном оборудовании (измерение давления, температуры, веса и т.п.), когда не требуется высокая частота дискретизации и необходимо разрешение более 16 разрядов. Принцип работы сигма-дельта АЦП сложнее для понимания. Эта структура относится к классу интегрирующих АЦП. Но основная особенность сигма-дельта АЦП состоит в том, что частота следования выборок, при которых собственно и происходит анализ уровня напряжения измеряемого сигнала, существенно превышает частоту появления отсчетов на выходе АЦП (частоту дискретизации). Эта частота следования выборок называется частотой передискретизации. Так, сигма-дельта АЦП со скоростью преобразования 100 К отсчетов/сек, в котором используется частота передискретизации в 128 раз больше, будет производить выборку значений входного аналогового сигнала с частотой 12.8 М отсчетов/сек. Порядок модулятора определяется численностью интеграторов и сумматоров в его схеме. Сигма-дельта модуляторы N-гo порядка содержат N сумматоров и N интеграторов и обеспечивают большее соотношение сигнал/шум при той же частоте отсчетов, чем модуляторы первого порядка. Примерами сигма-дельта модуляторов высокого порядка являются одноканальный AD7720 седьмого порядка и двухканальный ADMOD79 пятого порядка. Наиболее широко в составе ИМС используются однобитные сигма- дельта модуляторы, в которых в качестве АЦП используется компаратор, а в качестве ЦАП – аналоговый коммутатор (рис. 6.13). 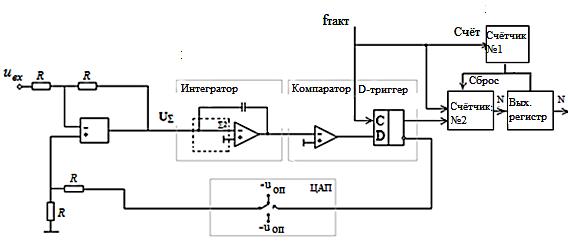 Рис. 6.13. Структурная схема сигма-дельта АЦП первого порядка Принцип действия пояснен в табл.6.2 на примере преобразования входного сигнала, равного 0,6 В, при Uoп = +1B и -1B. Пусть постоянная времени интегрирования интегратора численно равна периоду тактовых импульсов. В нулевом периоде выходное напряжение интегратора сбрасывается в нуль. На выходе ЦАП также устанавливается нулевое напряжение. Затем схема проходит через последовательность состояний (табл. 6.2), UK - состояние компаратора в битах. Таблица 6.2 Иллюстрация работы сигма-дельта АЦП
В тактовые периоды 2 и 7 состояния системы идентичны, так как при неизменном входном сигнале UBX = 0,6 В цикл работы занимает пять тактовых периодов. Усреднение выходного сигнала ЦАП за цикл действительно дает величину напряжения 0,6 В (1-1+1+1+1)/5 = 0,6. Это доказывает корректность работы сигма-дельта модулятора. Входной сигнал поступает на инвертирующий вход дифференциального усилителя, а на неинвертирующий - выход одноразрядного ЦАП. Таким образом дифференциальный усилитель служит элементом сравнения (вычитающим устройством). Интегратор - это активный аналоговый ФНЧ с высоким усилением в полосе частот входного сигнала и подавлением частотных составляющих, лежащих вне этой полосы. Квантователь - это в первом приближении компаратор с порогом срабатывания, равным "0", выход которого может переключаться из состояния "-Uoп" в состояние "+Uоп", и который подключен ко входу синхронизируемого тактовой частотой (частотой дискретизации) элемента памяти, сохраняющего это состояние в течение тактового интервала. Если предположить, что на выходе этого элемента памяти, который одновременно является и выходом с уровнями модулятора, должен формироваться цифровой сигнал соответствующий уровням логического "нуля" и "единицы" (АЦП), то таким элементом памяти может служить обычный D-триггер. Правда, в петле обратной связи при этом понадобится отдельное переключающее устройство, выполняющее функции ЦАП (на рис.6.13 показано штриховой линией), который управляется цифровым сигналом, а на выходе формирует либо "-Uoп", либо "+Uoп". Дополнительным и очень важным достоинством сигма-дельта АЦП является то, что все его внутренние узлы могут быть выполнены интегральным способом на площади одного кремниевого кристалла. Это заметно снижает стоимость конечных устройств и повышает стабильность характеристик АЦП. Способ формирования многоразрядных отсчётов на выходе сигма- дельта модулятора зависит от того, какова требуется разрядность этих отсчётов и с какой скоростью они должны следовать. Повышение разрядности и скорости следования отсчётов (частоты дискретизации Fд) усложняет задачу и ограничивает выбор средств, с помощью которых эта задача может быть решена. Наиболее простым способом получения многоразрядных отсчётов на выходе сигма-дельта модулятора является подсчёт количества «единиц» в цифровом потоке, формируемом одноконтурным сигма-дельта модулятором 1-го порядка, за период дискретизации Тд=1/ Fд . Если заданы частота дискретизации Fд и разрядность выходного кода m, то тактовая частота Fт, на которой работает сигма-дельта модулятор, должна быть выше частоты дискретизации в k раз Fт = k·Fд , где k = 2m (при максимальном Uвх все разряды счётчика 2 должны быть установлены в «единицы»). Тогда интервал времени равный периоду дискретизации, можно сформировать путём деления тактовой частоты FT на число k с помощью обычного счётчика (счётчик 1). Подсчет «единиц» в цифровом потоке также осуществляется с помощью счетчика (счетчик 2), причем на его счетный вход подается та же тактовая частота FT, а на вход разрешения счета поступают «единицы» кода. Когда на входе разрешения присутствует «единица», счетчик увеличивает свое содержание, а когда «0» — состояние остается прежним. В конце каждого периода дискретизации сигналом со счетчика 1 содержимое счетчика 2 переписывается в N-разрядный выходной регистр, а сам счетчик 2 обнуляется. Таким образом, на выходе АЦП формируется код отсчета, численно равный количеству «единиц» в цифровом потоке на выходе D-триггера за период дискретизации. Описанный метод чрезвычайно прост, но обладает невысокой точностью и применим только для квантования медленно меняющихся процессов или в случае, когда высокой точности не требуется. Если же сигнал на входе преобразователя меняется быстро (следовательно, частота дискретизации должна быть велика) и необходимо получить высокое разрешение, то использование данного метода становится невозможным. В подобных случаях пользуются другими методами построения сигма-дельта АЦП — применением модуляторов 2-го и более высоких порядков, каскадным соединением таких модуляторов, использованием многоразрядных квантователей и многоразрядных ЦАП в петле обратной связи, а на выходе размещают сложные цифровые фильтры высоких порядков, выполняющие операцию децимации (прореживания) одноразрядного цифрового потока - вместе с увеличением разрядности выходного кода. Интегрирующие АЦП. И последний тип АЦП, о котором пойдет здесь речь - АЦП двухтактного интегрирования. В цифровых мультиметрах, как правило, используются именно такие АЦП, т. к. в этих измерительных приборах необходимо сочетание высокого разрешения и высокого помехоподавления. Идея преобразования в таком интегрирующем АЦП гораздо менее сложна, чем в сигма-дельта АЦП. На рис.6.14 показан принцип работы АЦП двухтактного интегрирования. 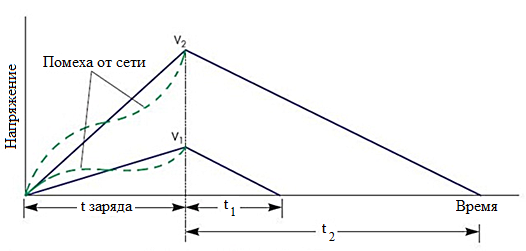 Рис. 6.14. Интегрирующий АЦП. Пунктиром выделена помеха от сети Входной сигнал заряжает конденсатор в течение фиксированного периода времени, который обычно составляет один период частоты питающей сети (50 или 60 Гц) или кратен ему. При интегрировании входного сигнала в течение промежутка времени такой длительности высокочастотные помехи подавляются. Одновременно исключается влияние нестабильности напряжения сетевого источника питания на точность преобразования. Это происходит потому, что значение интеграла от синусоидального сигнала равно нулю, если интегрирование осуществляется во временном интервале, кратном периоду изменения синусоиды. По окончании времени заряда АЦП разряжает конденсатор с фиксированной скоростью, в то время как внутренний счетчик подсчитывает количество тактовых импульсов за время разряда конденсатора. Большее время разряда, таким образом, соответствует большему значению показаний счетчика и большему измеряемому напряжению (рис. 6.14). АЦП двухтактного интегрирования имеют высокую точность и высокую разрешающую способность, а также имеют сравнительно простую структуру. Это дает возможность выполнять их в виде интегральных микросхем. Основной недостаток таких АЦП - большое время преобразования, обусловленное привязкой периода интегрирования к длительности периода питающей сети. Например, для 50 герцового - оборудования частота дискретизации АЦП двухтактного интегрирования не превышает 25 отсчетов/сек. Конечно, такие АЦП могут работать и с большей частотой дискретизации, но при увеличении последней помехозащищенность падает. Применение АЦП. Аналого-цифровое преобразование используется везде, где требуется обрабатывать, хранить или передавать сигнал в цифровой форме: • АЦП являются составной частью систем сбора данных; • быстрые видео АЦП используются, например, в ТВ-тюнерах (это параллельные и конвейерные АЦП); • медленные встроенные 8, 10, 12 или 16-битные АЦП часто входят в состав микроконтроллеров (как правило они строятся по принципу поразрядного уравновешивания, точность их невысока); • очень быстрые АЦП необходимы в цифровых осциллографах (параллельные и конвейерные); • современные весы используют АЦП с разрядностью до 24 бит, преобразующие сигнал непосредственно от тензометрического датчика (сигма-дельта АЦП); • АЦП входят в состав радиомодемов и других устройств радиопередачи данных, где используются совместно с процессором цифровой обработки сигналов в качестве демодулятора; • сверхбыстрые АЦП используются в антенных системах базовых станций (в так называемых SMART-антеннах) и в антенных решетках радиолокационных станций. Если структура САУ создается на базе микропроцессора или PIC-контроллера (Peripheral Interface Controller – периферийный контроллер интерфейса), то приходится все управляющие аналоговые сигналы, определяющие работу и качественные показатели системы, преобразовывать в цифровую форму. Количество типов выпускаемых сегодня в мире интегральных АЦП в виде автономных микросхем, а также встроенных в структуру PIC-контроллеров огромно и учитывает запросы разработчиков САУ с точки зрения параметров точности и быстродействия. Но при этом приходится учитывать и другие проблемы при выборе конкретного типа АЦП. Учет частоты дискретизации (максимальная скорость Найквиста, Fн). Эта величина обычно приводится как справочная для любого типа АЦП (как для автономных микросхем, так и встроенных в другие устройства). Обычно разработчики САУ в большинстве случаев сравнивают Fн с частотой среза 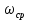 проектируемой системы. Если объект управления инерционный (нагревательный элемент, электродвигатели и др.), то проблем по этому критерию не возникает. Только необходимо помнить, что частота Fн отображается в величине частоты (Гц), а частота проектируемой системы. Если объект управления инерционный (нагревательный элемент, электродвигатели и др.), то проблем по этому критерию не возникает. Только необходимо помнить, что частота Fн отображается в величине частоты (Гц), а частота 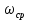 в величине круговой частоты (рад/сек). в величине круговой частоты (рад/сек).Учет количества каналов (К). С целью экономии количества автономных микросхем АЦП могут иметь несколько входных аналоговых каналов, которые с помощью коммутатора подключаются к одной и той же схеме преобразователя в цифровую форму. И для корректности выбора по частоте Fн необходимо учитывать время преобразования всех каналов. Поэтому приходится сравнивать частоту 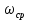 с величиной Fн/K, где K – число используемых каналов. с величиной Fн/K, где K – число используемых каналов.Учет электрических параметров аналогового сигнала. Максимальная величина напряжения Uвх обычно является справочной величиной. Если Uвх.max больше этой величины, то необходимо следить, чтобы Uвх.max < Uвх. Учет разрядности АЦП. С целью уменьшения различного рода ошибок САУ обычно стремятся выбирать АЦП с большой разрешающей способностью (большой разрядностью), что не всегда является оптимальным решением. Особенно это утверждение справедливо для PIC-контроллеров, которые стандартно работают с байтовой информацией (8 разрядов). Если разрядность АЦП больше, то приходится создавать более сложные алгоритмы обработки информации с двойной точностью (16 разрядов). Обычно в библиотеке любого PIC-контроллера имеются такие программы. Но это потребует увеличения времени обработки информации, дополнительной памяти для их хранения. Последнее требование может создать непреодолимую задачу для выбранного типа АЦП. Такая же проблема нехватки памяти возникает при отказе работы с целочисленной арифметикой в пользу арифметических действий с реальными данными, которые хранятся в виде мантиссы и порядка, из-за использования соответствующих библиотечных программ. Если в структуре САУ используется более мощный микропроцессор с возможностью работы с действительными числами, то обычно в их структуре отсутствуют встроенные АЦП и приходится использовать автономные микросхемы. Такая организация САУ рождает проблему организации интерфейса по управлению коммутатором входных аналоговых сигналов и считывание выходных цифровых данных (эти интерфейсы строятся на базе PIС-контроллеров). Стандартно мощные микропроцессоры имеют для связи с другими внешними устройствами последовательный порт. При таком подходе следует выбирать АЦП с последовательной передачей информации (выпускаются АЦП и с параллельной передачей данных), которая побитно передается в другое устройство в течение определенного промежутка времени. Вид аналогового сигнала. Существуют АЦП, которые преобразуют однополярный аналоговый сигнал (обычно положительный) или биполярный. Но выходная информация представлена в прямом коде в виде только положительных чисел. В САУ обычно приходится работать с биполярными сигналами, производить арифметические операции и с отрицательными сигналами, которые в процессоре должны быть представлены со своими знаками. Если АЦП униполярный, то входной сигнал с помощью суммирующего усилителя и сигнала смещения Uсм необходимо преобразовывать в положительный. Но необходимо программным образом предусмотреть вычитание АЦП цифрового эквивалента Uсм. Та же процедура необходима и при биполярном АЦП (вычитание эквивалента Uсм=0). В процессе проектирования САУ с АЦП могут возникнуть и другие проблемы. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
