Занятие Тема Основные понятия химической

• Название: Занятие Тема Основные понятия химической
• Дата: 16.03.2023
• Размер: 93.86 Kb.
• Имя файла: kinetics_problem.docx
• Тип: Занятие; #995459
• страница: 4 из 4

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

1. 
   Экспериментально определено, что скорость химической реакции
   

CO + Cl₂ = COCl₂

в любой момент времени протекания реакции равна:

v= k(c

)⁰ (c

)^1,5 _.

CO Cl₂

Укажите общий порядок данной реакции. Можно ли считать, что данная реакция является элементарной? Зависит ли скорость протекания этой реакции от концентрации СО?

2. 
   Реакция
   

2N₂O₅ = 2N₂O₄ + O₂

протекает в газовой фазе. Скорость

данной реакции равна:

v= kp²


N O
2 5

. Укажите порядок реакции. Запишите

уравнение, связывающее общую скорость реакции со скоростями по отдельным веществам.

3. 
   Реакция
   

2CO + O₂ = 2CO₂

является формально простой. Найдите

порядок данной реакции по каждому веществу и общий порядок этой реакции.

На основе метода формальной кинетики запишите уравнение, связывающее общую скорость реакции со скоростями по отдельным веществам.

4. 
   Укажите порядок простой реакции по каждому веществу и общий порядок реакции
   

2А = 4В + С

На основе метода формальной кинетики запишите уравнение, свя- зывающее общую скорость реакции со скоростями по отдельным веще- ствам.

5. 
   Укажите порядок реакции по каждому веществу и общий порядок реакции, если она протекает в одну стадию
   

2А + В = 2С + D + E

На основе метода формальной кинетики запишите уравнение, свя- зывающее общую скорость реакции со скоростями по отдельным веще- ствам.

6. 
   Укажите порядок реакции по каждому веществу и общий порядок реакции, если она протекает в одну стадию
   

А + В = 2С + D

На основе метода формальной кинетики запишите уравнение, свя- зывающее общую скорость реакции со скоростями по отдельным веще- ствам.

7. 
   Реакция изомеризации
   

CH₃NC = CH₃CN

которая протекает в газовой фазе, имеет первый порядок по компоненту при высоких давлениях и второй — при низких. Как будут выглядеть выражения для скорости реакции по исходному веществу в первом и во втором случаях?

8. 
   Скорость газ фазной реакции
   

2N₂O₅ = 2N₂O₄ + O₂
может быть выражена через парциальное давление p_i, концентрацию c_iи изменение количества молей одного из веществ. Получите соотношения, связывающие эти выражения.

9. 
   Химическая реакция
   

H O + Cr O^2- = 2CrO^2- + 2H⁺

2 2 7 4

которая протекает в жидкой фазе, характеризуется кинетическим урав- нением, идентичным стехиометрическому. Запишите уравнение, связы- вающее общую скорость реакции со скоростями по отдельным вещест-

вам. Установите связь между pH и концентрацией

Cr O^2 , если в перво-

2 7
начальный момент времени продукты реакции отсутствовали и вода взята в большом избытке.

10. 
    Как соотносятся величины константы скорости для реакции третьего порядка, если концентрации выражены в 1/см³ и моль.
    

Практическое занятие 2

Тема: Влияние температуры на скорость химических реакций

Цель:

С повышением температуры скорость большинства реакций увеличивается. Зависимость скорости реакции от температуры, выраженная графически, дает круто поднимающуюся кривую. Так как концентрации компонентов, участвующих в реакции, при повышении температуры не изменяются, то изменение скорости реакции с температурой обусловлено изменением константы скорости.

Для количественного описания зависимости константы скорости от температуры в химической кинетике используют два основных соотношения: правило Вант-Гоффа и уравнение Аррениуса.

Правило Вант-Гоффа говорит о том, что при повышении температуры на 10 градусов константа скорости химической реакции увеличивается в 2–4 раза: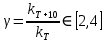



где  — температурный коэффициент скорости химической реакции. В общем случае для повышения температуры от T1 до T2 отношение констант скоростей равно: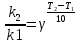



Правило Вант-Гоффа приближенное и применимо только в очень ограниченном интервале температур, так как температурный коэффициент изменяется с температурой. Для большинства реакций зависимость константы скорости от температуры описывается уравнением Аррениуса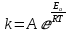



Это уравнение содержит два параметра, которые не зависят от температуры: А — предэкспоненциальный множитель, который определяется только типом реакции; Еa — энергия активации химической реакции, которая характеризует высоту энергетического барьера на пути реакции. Экспоненциальный множитель в уравнении Аррениуса можно интерпретировать, как долю молекул, энергия которых превышает Еa при температуре Т.

Предэкспоненциальный множитель А имеет ту же размерность, что и константа скорости, и для реакций первого порядка может быть выражена в обратных секундах. Поскольку в таких единицах выражается частота, величину А иногда называют фактором частоты.

Уравнение Аррениуса (5.3) в дифференциальной форме можно записать как: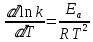



Разделив переменные k и T и считая Ea постоянной величиной, после интегрирования (5.4) получим: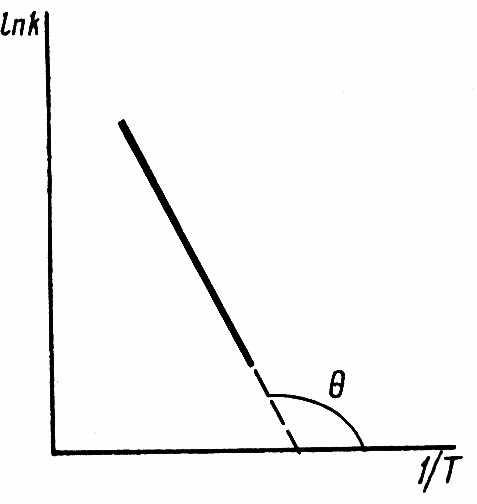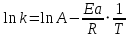


Если уравнение (5.5) справедливо, то на графике в координатах lnk–1/T (рис. 5.1) опытные точки располагаются на прямой линии под углом  к оси абсцисс и угловым коэффициентом (тангенсом угла наклона), равным –Еa/R, что позволяет рассчитать энергию активации химической реакции по зависимости константы скорости от температуры: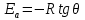

Энергию активации химической реакции можно вычислить по значениям констант скоростей при двух разных температурах. Запишем уравнение (5.5) для температур Т1 и Т2 и вычтем первое уравнение из второго: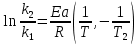

Уравнение для расчета энергии активации химической реакции имеет вид: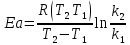



Если данные о величине константы скорости неизвестны, то вместо константы скорости в уравнении Аррениуса можно подставить другие, связанные с ней величины. Например, начальные скорости реакции при разных температурах или время, за которое выход продукта реакции составит заданную величину при разных температурах. В качестве таких данных можно использовать время полупревращения при разных температурах. Уравнение Аррениуса содержит всего два параметра. Для более точного описания экспериментальных данных было предложено трехпараметрическое уравнение: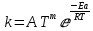



в котором учитывается зависимость предэкспоненциального множителя от температуры. Для реакций, у которых предэкспоненциальный множитель зависит от температуры, определяют эффективную или опытную энергию активации по уравнению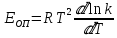



Подставляя уравнение (5.9) в (5.10), находим, что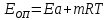



Данные соотношения справедливы не для всех реакций. Например, аномальная зависимость константы скорости от температуры наблюдается иногда для реакций третьего порядка, когда константа скорости с ростом температуры убывает; для некоторых ферментативных реакций константа скорости сначала возрастает, а потом убывает. Всякий раз такие явления требуют особого объяснения исходя из механизмов этих реакций. Энергии активации в уравнениях Аррениуса для прямой и обратной реакции связаны друг с другом через изменение внутренней энергии для суммарной реакции. Если кинетическое уравнение для реакции идеальных газов написать через концентрации, то константы скорости для прямой и обратной реакций (k1 и k2) связаны с константой равновесия Kс соотношением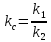



Логарифмируя обе части уравнения (5.11) и дифференцируя их по абсолютной температуре, получим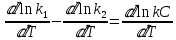



Учитывая уравнение изохоры химической реакции: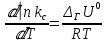



находим, что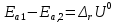

Таким образом, разность энергий активации для прямой и обратной реакций равна изменению внутренней энергии для суммарной реакции.