Методы оптимальных решений. Задание 1. Запишем все варианты раскроя Длина заготовок, м
 Скачать 0.73 Mb. Скачать 0.73 Mb.
|
 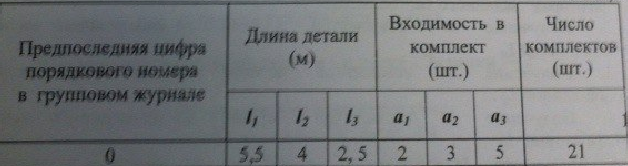  Запишем все варианты раскроя:
1. Составьте математическую модель получения максимального количества комплектов деталей из всех заготовок. Для этого вводится еще одна переменная: x20 – количество комплектов деталей. При этом математическая модель для случая трех видов заготовок и комплектов, состоящих из трех видов деталей, записывается следующим образом. Целевая функция: x0 =x20 (max) . Система ограничений: – по комплектности: 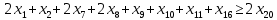 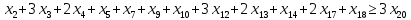 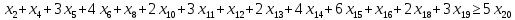 – по ресурсам заготовок: 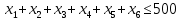 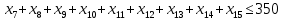 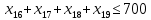 Условие неотрицательности и целочисленности переменных: 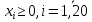 2. Составьте математическую модель получения Мкомплектов деталей из наименьшего числа заготовок длиной L1. Математическая модель для случая использования только заготовок первого типа, а комплекты состоят из деталей 3 видов, записывается следующим образом. Целевая функция: 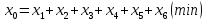 Система ограничений: – по комплектности: 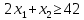 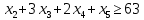 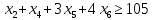 – по ресурсам заготовок длиной L1: 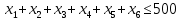 Условие неотрицательности и целочисленности переменных: 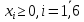 3. Составьте математическую модель получения Мкомплектов деталей из наименьшего числа заготовок длиной L2. Математическая модель для случая использования только заготовок первого типа, а комплекты состоят из деталей 3 видов, записывается следующим образом. Целевая функция: 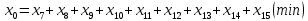 Система ограничений: – по комплектности: 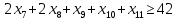 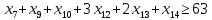 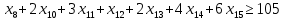 – по ресурсам заготовок длиной L2: 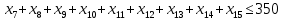 Условие неотрицательности и целочисленности переменных: 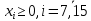 4. Составьте математическую модель получения Мкомплектов деталей из наименьшего числа заготовок длиной L3. Математическая модель для случая использования только заготовок первого типа, а комплекты состоят из деталей 3 видов, записывается следующим образом. Целевая функция: 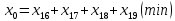 Система ограничений: – по комплектности: 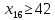 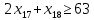 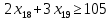 – по ресурсам заготовок длиной L2: 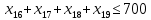 Условие неотрицательности и целочисленности переменных: 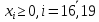 5. Составить математическую модель получения Мкомплектов деталей из всех заготовок данного типоразмера при минимальных отходах материала. Математическая модель при использовании заготовок всех типов и Мкомплектов, состоящих из деталей трех видов, записывается следующим образом. Целевая функция: 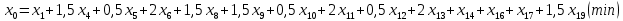 Система ограничений: – по комплектности: 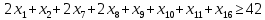 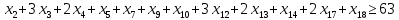 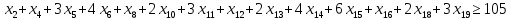 – по ресурсам заготовок: 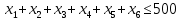 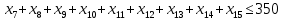 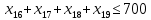 Условие неотрицательности и целочисленности решений: 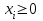 , xi – целое, где , xi – целое, где 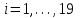 . . | |||||||||||||||||||||||||||||||||||||||
