Курсова робота_СТАРАЯ. Зміст

• Название: Зміст
• Дата: 17.12.2020
• Размер: 1.63 Mb.
• Имя файла: Курсова робота_СТАРАЯ.docx
• Тип: Задача; #161615
• страница: 3 из 8

Нейронні мережі для задачі розпізнавання

Одним із способів представлення класифікатора для машинного навчання є нейронні мережі.

Спочатку область нейронних мереж була натхненна ціллю моделювання біологічних нейронних систем, але з тих пір вона розійшлася і стала питанням інженерії та досягнення хороших результатів у завданнях з машинного навчання.

Основною обчислювальною одиницею мозку є нейрон. Приблизно 86 мільярдів нейронів можна знайти в нервовій системі людини, і вони пов'язані з приблизно 1014 - 1015 синапсами. На рисунку 1.5 показано схему біологічного нейрона.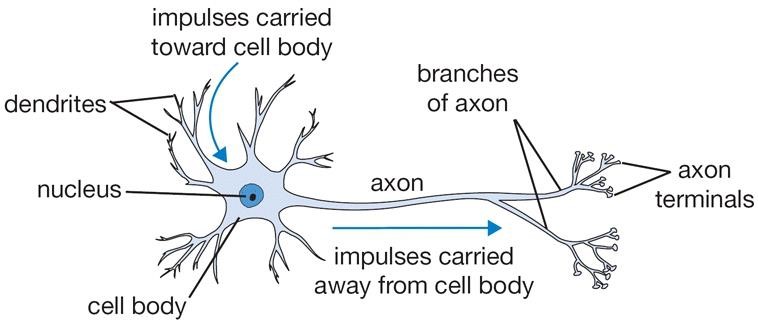


Рисунок 1.5 – Біологічна модель нейрона
На рисунку 1.6 представлена загальна математична модель. Кожен нейрон отримує вхідні сигнали від своїх дендритів і виробляє вихідні сигнали вздовж його (єдиного) аксона. Аксон з часом розгалужується і з'єднується через синапси з дендритами інших нейронів. У розрахунковій моделі нейрона сигнали, які рухаються уздовж аксонів (наприклад, x0), мультиплікативно взаємодіють (наприклад, w0x0) з дендритами іншого нейрону, виходячи з синаптичної сили на цьому синапсі (наприклад, w0). Ідея полягає в тому, що синаптичні сили (ваги w) можуть навчатися і контролюють силу впливу (і його напрям: збудливий (позитивний вага) або інгібіторний (негативний вага)) одного нейрона на інший. У базовій моделі дендрити несуть сигнал до тіла комірки, де всі вони отримують підсумки. Якщо остаточна сума перевищує певний поріг, нейрон може спрацювати, посилаючи імпульс уздовж його аксона. У розрахунковій моделі ми припускаємо, що точні таймінги імпульсів не мають значення, і що тільки частота спрацьовування передає інформацію. Виходячи з цієї частотної інтерпретації коду, ми моделюємо частоту спрацювання нейрона як активаційну функцію f, яка відображає частоту імпульсів вздовж аксона. Історично загальним вибором функції активації є сигмоподібна функція σ, оскільки вона приймає справжнє значення входу (сила сигналу після суми) і розподіляє її на відстань між 0 і 1.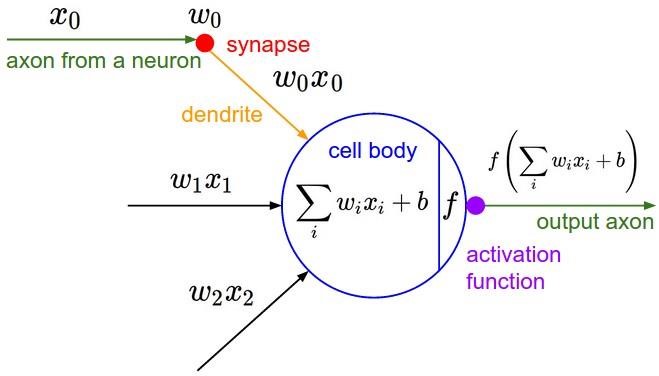


Рисунок 1.6 – Математична модель нейрона

Пряме проходження нейрону можна описати так, як зображено на рисунку 1.7.

class Neuron(object): # ... def forward(self, inputs): """ assume inputs and weights are 1-D numpy arrays and bias is a number """ cell_body_sum = np.sum(inputs * self.weights) + self.bias firing_rate = 1.0 / (1.0 + math.exp(-cell_body_sum)) # sigmoid activation function return firing_rate

Рисунок 1.7 – Код для прямого проходження нейрона

Іншими словами, кожен нейрон виконує скалярне множення його входу із його вагами, додає зміщення та застосовує нелінійність (або функцію активації), в цьому випадку сигмоїду.

1.3.1 Найпопулярніші активаційні функції

Sigmoid (Сигмоїда). Сигмоїдна нелінійність представлена у формулі (𝑥) = 1/(1 + 𝑒−𝑥), а її графік на рисунку 1.8: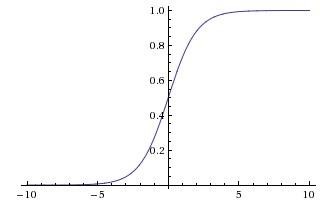



Рисунок 1.8 - Сигмоїдальна нелінійність
Вона приймає дійсне число і "стискує" його в діапазон від 0 до 1. Зокрема, великі негативні числа стають 0, а великі позитивні числа стають 1. Сигмоїдна функція часто зустрічається в історичному відношенні оскільки вона має приємну інтерпретацію як швидкість руху нейрона: від не спрацювання зовсім (0) до повністю насиченого спрацювання при прийнятній максимальної частоті (1). На практиці сигмоїдна нелінійність останнім часом випала з користі, і вона рідко використовується. Вона має два основних недоліки:

• 
  Сигмоїда насичується і вбиває градієнти. Дуже небажаним властивістю сигмоєвидного нейрону є те, що коли активація нейрона насичується в будь-якому хвості від 0 або 1, градієнт у цих областях майже дорівнює нулю. При зворотному розповсюдженні цей (локальний) градієнт буде помножений на градієнт виходу цього нейрону. Тому, якщо локальний градієнт дуже малий, він фактично «вб'є» градієнт, і практично не буде ніякого сигналу протікати через нейрон до його ваг та рекурсивно до його даних. Окрім того, потрібно приділяти особливу обережність при ініціалізації ваг сигмоєвидних нейронів, щоб запобігти насиченість. Наприклад, якщо початкові ваги занадто великі, більшість нейронів стануть насиченими, і мережа ледь навчиться.
  
• 
  Виходи сигмоїди не нульові. Це небажано, оскільки нейрони у більш пізніх шарах обробки в нейронній мережі будуть отримувати дані, які не нульові. Це має наслідки для динаміки під час градієнтного спуску, тому що якщо дані, що надходять в нейрон, завжди позитивні (наприклад, x> 0 елементарно в f = wTx + b)), то градієнт на вагах w при зворотному поширенні стане будь-яким з усіх позитивний або усіх негативних (залежно від градієнта всього виразу f). Після того, як ці градієнти будуть додані до частини даних, остаточне оновлення для ваг може мати змінні ознаки, що трохи пом'якшує цю проблему. Тому це є незручно, але має менш серйозні наслідки в порівнянні з насиченою проблемою активації вище.
  

Tanh (Тангенсоїда, тангенційна нелінійність). Ця функція обмежує дійсне число до діапазону [-1, 1]. Подібно сигмоєвидному нейрону, його активація насичується, але на відміну від сигмовидного нейрона його вихід є відцентрованим відносно нуля. Тому на практиці віддають перевагу тангенційній нелінійності, ніж сигмоподібній нелінійності. Тангенційний нейрон - це масштабований сигмоподібний нейрон, його функція представлена у формулі 𝑡𝑎𝑛ℎ(𝑥) = 2(2𝑥) − 1, а графік зображено на рисунку 1.9.

ReLU (Rectified Linear Unit). Активаційна функція ReLU стаkf дуже популярним протягом останніх кількох років. Її математична формула виглядає так 𝑓(𝑥) = 𝑚𝑎𝑥(0,𝑥), а її графік зображено на рисунку 1.10.

Іншими словами, активація – це просто перетин нуля. Є кілька плюсів і мінусів до використання ReLU:

(+) Знайдено значне прискорення збіжності стохастичного градієнтного походження порівняно з функціями Sigmoid / Tanh. Стверджується, що це пов'язано з його лінійною, не насичуючою формою.

(+) У порівнянні з Tanh / Sigmoid нейронами, що передбачають дорогі операції (експоненти тощо), ReLU може бути реалізований шляхом простого перетинання матриці активації нуля.

(-) На жаль, нейрони ReLU можуть бути нестабільними під час тренувань і можуть «вмирати». Наприклад, великий градієнт, що протікає через нейрон ReLU, може призвести до оновлення ваг таким чином, що нейрон більше ніколи не активується на будь-яких даних. Якщо це станеться, градієнт, що протікає через нейрон, назавжди стане нульовим з цієї точки. Тобто нейрони ReLU можуть незворотно вмирати під час тренувань. Наприклад, ви можете виявити, що до 40% вашої мережі може бути "мертвою" (тобто нейронами, які ніколи не активуються по всьому навчальному набору даних), якщо швидкість навчання встановлена занадто висока. При правильному налаштуванні швидкості навчання це рідше є проблемою.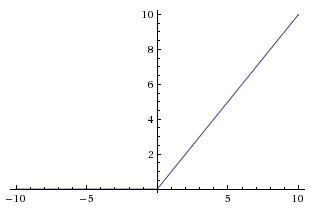


Рисунок 1.10 - Активаційна функція Left: Rectified Linear Unit (ReLU)

1.3.2 Архітектура нейронних мереж

Шарова організація. Нейронні мережі – це нейрони, що об’єднані у граф. Нейронні мережі моделюються як набір нейронів, які пов'язані в ациклічному графі. Іншими словами, виходи деяких нейронів можуть стати входи інших нейронів. Цикли не дозволяються, оскільки це означатиме нескінченний цикл у прямому проході мережі. Моделі нейронної мережі часто організовуються в різні шари нейронів. Для звичайних нейронних мереж найпоширенішим типом шару є повністю з'єднаний шар, в якому нейрони між двома сусідніми шарами повністю попарно пов'язані, але нейрони в одному шарі не мають спільних зв'язків. На рисунках 1.11 і 1.12 наведено два приклади топологій нейронної мережі, які використовують повнозв’язні шари: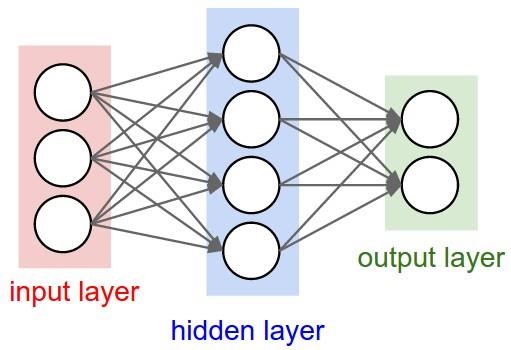


Рисунок 1.11 - Двошарова нейронна мережа та три входи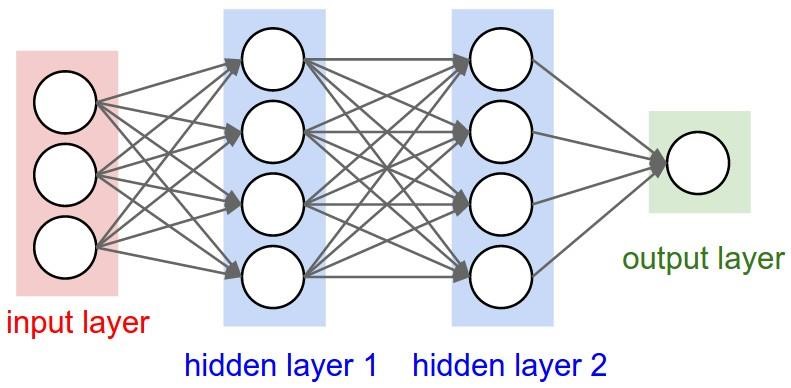



Рисунок 1.12 - Тришарова нейронна мережа
Вихідний шар. На відміну від всіх шарів нейронної мережі, найчастіше нейрони вихідного шару не мають функції активації (або іншими словами, що вони мають лінійну функцію активації ідентичності). Це пояснюється тим, що останній вихідний рівень зазвичай приймається для представлення класів (наприклад, за класифікацією), які є довільними дійсними числами, або певною ціллю дійсного значення (наприклад, у регресії).

Пряме проходження нейронної мережі (feed-forward computation). Повторне множення матриць переплітається з функцією активації. Однією з основних причин того, що нейронні мережі організовані в шари, полягає в тому, що ця структура робить дуже простим та ефективним оцінювання нейронних мереж за допомогою матричних векторних операцій. Працюючи з прикладом тришарової нейронної мережі на схемі вище, вхід буде вектором [3x1]. Всі ваги зв’язків для шару можна зберігати в одній матриці. Наприклад, перша вага прихованого шару W1 буде мати розмір [4x3], а зміщення для всіх нейронів будуть у векторі b1 розміру [4x1]. Тут кожен окремий нейрон має ваги в рядку W1, тому множення матричного вектора np.dot (W1, x) оцінює активацію всіх нейронів у цьому шарі. Аналогічно, W2 буде матрицею [4x4], яка зберігає зв'язки другого прихованого шару, а W3 - [1x4] матрицю для останнього (вихідного) шару. Повне пряме проходження цієї тришарової нейронної мережі - це просто три матричних множення, переплетені із застосуванням функції активації, що зображені на рисунку 1.13:


Рисунок 1.13 – Пряме проходження тришарової нейронної мережі

У наведеному вище коді W1, W2, W3, b1, b2, b3 – це параметри, є навчальними параметрами мережі. Замість одиничного вектора-стовпчика входу, х може містити цілу набір тренувальних даних (де кожен приклад буде колонкою з x), а потім всі приклади будуть ефективно оцінюватися паралельно. Зверніть увагу, що останній шар нейронної мережі, як правило, не має функції активації (наприклад, він являє собою (реально оцінену) оцінку класу в установці класифікації).

Один із способів розглянути нейронні мережі з повнозв’язнимими шарами полягає в тому, що вони визначають сукупність функцій, параметризованих вагами мережі.

Нейронні мережі, що містять принаймні один прихований шар - універсальні апроксиматори. Тобто, це може бути показано, що за умови неперервної функції f (x) та деякого ε> 0 існує нейронна мережа g (x) з одним прихованим шаром (з розумним вибором нелінійності, наприклад сигмовидної), такими, що x, | f (x) - g (x) | <ε. Іншими словами, нейронна мережа може наближати будь-яку неперервну функцію.

Якщо одного прихованого шару достатньо, щоб наблизити будь-яку функцію, чому використовують більше шарів? Відповідь полягає в тому, що той факт, що двошарова нейронна мережа є універсальним апроксиматором, при цьому є відносно слабким і не корисним твердженням на практиці. В одному вимірі функція, що зображена у формулі 𝑔(𝑥) = ∑𝑖 𝑐𝑖1(𝑎𝑖 < 𝑥 < 𝑏𝑖), де a, b, c є векторами параметрів, є також універсальним апроксиматором, але ніхто не вважає за потрібне використовувати цю функцію в машинному навчанні. Нейронні мережі добре працюють на практиці, тому що вони компактно виражають гладкі функції, які добре відповідають статистичним властивостям даних, які ми зустрічаємо на практиці, а також легко навчати за допомогою наших алгоритмів оптимізації (наприклад, градієнтного спуску). Аналогічним чином, той факт, що глибші мережі (з декількома прихованими шарами) можуть працювати краще, ніж мережі з одним-прихованим шаром, є емпіричним спостереженням, незважаючи на те, що їхня представницька сила рівна.

Як на відміну, на практиці часто буває так, що 3-шарові нейронні мережі будуть перевищувати двошарові мережі, проте створення більш глибоких нейронних мереж (4, 5, 6 шарів) рідко допомагає набагато більше. Це суттєво контрастує зі згортковими нейронними мережами (Convolutional Neural Networks, CNN), де визначено, що глибина є надзвичайно важливим компонентом для гарної системи розпізнавання (наприклад, по порядку 10 навчальних шарів). Один аргумент для цього спостереження полягає в тому, що зображення містять ієрархічну структуру (наприклад, обличчя складені з очей, які складаються з країв та ін.), Тому кілька рівнів обробки створюють інтуїтивний сенс для даного домену даних.

Встановлення кількості шарів та їх розмірів. Як вирішити, яку архітектуру використовувати, коли необхідно розв’язати проблему на практиці? По-перше, при збільшенні розміру та кількості шарів в нейронній мережі, потужність мережі збільшується. Тобто, простір представлених функцій зростає, оскільки нейрони можуть співпрацювати, щоб виразити багато різних функцій. Наприклад, припустимо, що ми мали бінарну проблему класифікації в двох вимірах. Ми могли б тренувати три окремі нейронні мережі, кожен з яких має один прихований шар деякого розміру і отримати наступні класифікатори (рисунок 1.14):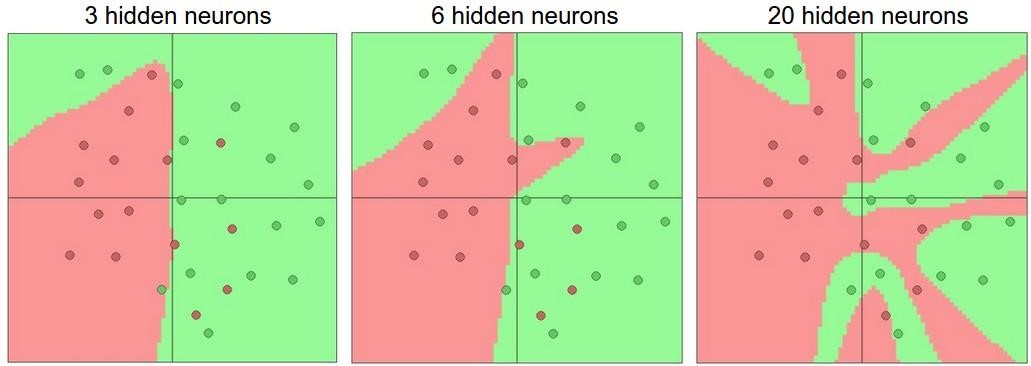


Рисунок 1.14 – Результати тренування мережі з 3, 6 та 20 нейронами у прихованому шарі

На наведеній вище схемі видно, що нейронні мережі з більшою кількістю нейронів можуть виразити більш складні функції. Проте це одночасно і добре (оскільки ми можемо навчитися класифікувати більш складні дані) і погано (оскільки простіше перенавчитись навчальним даним). Перенавчання відбувається, коли модель з високою ємністю підходить для шуму в даних, а не (як передбачається) взаємозв’язків між даними. Наприклад, модель з 20 прихованими нейронами підходить для всіх навчальних даних, але за ціною сегментації простору може неправильно розподіляти червоні та зелені сегменти. Модель з 3 прихованими нейронами має лише представницьку здатність класифікувати дані. Вона моделює дані у вигляді двох блоків і інтерпретує декілька червоних точок усередині зеленого кластера як викиди (шум). На практиці це може призвести до кращого узагальнення на тестовому наборі.

Перевага менших нейронних мереж може бути кращою, якщо дані недостатньо складні для запобігання перенавчання. Проте це неправильно - існує безліч інших переважних способів запобігання перенавчання в нейронних мережах. На практиці, завжди слід краще використовувати ці методи для контролю перенавчання, а не за кількістю нейронів.

Точна причина полягає в тому, що менші мережі важче тренувати за допомогою таких локальних методів, як градієнтний спуск: зрозуміло, що їх функції втрат мають порівняно небагато локальних мінімумів, але виявляється, що багато з цих мінімумів легше зближаються, і що вони погані (тобто з великою втратою). І навпаки, більші нейронні мережі містять значно більше локальних мінімумів, але ці мінімуми виявилися набагато кращими з точки зору їх фактичної втрати. Якщо ви тренуєте маленьку мережу, то остаточна втрата може відображати гарну кількість дисперсії - у деяких випадках вам пощастить і сходити в хорошому місці, але в деяких випадках ви потраппляєте в один з поганих мінімумів. З іншого боку, якщо ви тренуєте велику мережу, ви почнете знаходити багато різних рішень, але різниця в остаточному досягненні втрат буде набагато меншою. Інакше кажучи, всі рішення приблизно однаково добре, і менше покладаються на успіх випадкової ініціалізації.

Сила регуляризації - це найкращий спосіб контролювати перенавчання нейронної мережі. Можна оцінити результати, що були досягнуті за трьома різними налаштуваннями: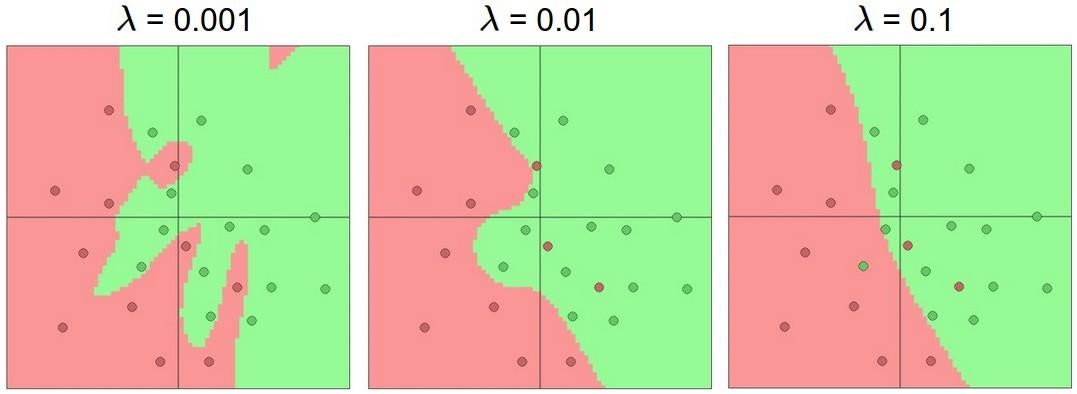


Рисунок 1.15 – Результати роботи нейронної мережі із різною силою регуляризації

Вихід – це те, що ви не повинні використовувати менші мережі, тому що ви боїтеся перенавчання. Замість цього, ви маєте використовувати як велику нейронну мережу, як дозволяє ваш обчислювальний бюджет, а також використовувати інші методи регуляризації для контролю за перенавчанням.