золотое сечение. Золотое сечение
 Скачать 0.99 Mb. Скачать 0.99 Mb.
|
|
Урок № 8. Тема : Золотое сечение. Тип урока: Урок комплексного применения знаний. Цели урока: Создать условия для применения знаний и умений в знакомой и новой учебных ситуациях. Вырабатывать умения выполнять практические задания по измерению длин, составлять отношения, проводить необходимые вычисления, анализировать полученные результаты и делать выводы. Оборудование урока.: карточки задания для измерения и составления отношений, портреты математиков древности, измерительные и чертежные инструменты, фотографии с видами села Селезениха, рисунки растений , фотографии , калькулятор. Содержание урока
 - это деление отрезка, при котором длина его большей части так относится к длине всего отрезка, как длина меньшей части к большей. Это отношение обозначают буквой 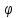 = 0, 618 = 0, 618
Анализ урока в компетентностном режиме. Исторические сведения и дополнительный материал к уроку Вопрос о математических предпосылках прекрасного, о роли математики в искусстве волновал еще древних греков, причем свой интерес они унаследовали от предшествующих цивилизаций. В наше время геометрия – необходимый элемент общего образования и культуры, представляет большой исторический интерес, имеет серьезное практическое применение и обладает внутренней красотой. Иогану Кеплеру принадлежат слова: «Геометрия владеет двумя сокровищами: одно из них – теорема Пифагора, другое – деление отрезка в среднем и крайнем отношении». Деление отрезка в среднем и крайнем отношении называют золотым сечением. В истории утвердилось еще одно название – «золотая пропорция». Пусть С АВ и производит, как говорят, «золотое сечение» отрезка. 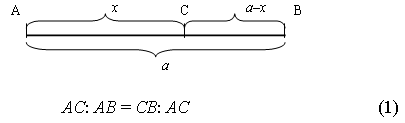 Золотым сечением называется такое деление отрезка, при котором большая часть так относится к целому, как меньшая часть к большей. Если длину отрезка АВ обозначить через а, а длину АС – через х, то а – х – длина отрезка СВ, и пропорция (1) примет вид: В пропорции, как известно, произведение крайних членов равно произведению средних и пропорцию (2) перепишем в виде: х2 = а(а – х). Получаем квадратное уравнение: х2 + ах – а2 = 0. Длина отрезка выражается положительным числом, поэтому из двух корней Число Но в практике пользуются числом , взятым с точностью или до тысячных 0,618, или до сотых 0,62, или до десятых 0,6. Если Таким образом, части «золотого сечения» составляют приблизительно 62 % и 38 % всего отрезка. Деление отрезка в среднем и крайнем отношении часто использовалось в искусстве, встречается оно и в живой природе, что дало повод математику XVI в., другу известного художника Леонардо да Винчи, монаху Луке Пачоли назвать такое деление отрезка божественной, великолепной пропорцией. По поводу этой пропорции он употребляет много слов, но в истории утвердились два варианта: золотая пропорция, или золотое сечение. Геометрически золотое сечение можно построить следующим образом: построим отрезок АВ, восстановим в точке В перпендикуляр к АВ на нем отложим точку D таким образом, чтобы BD =  Далее, соединив точки А и D, отложим DE = BD, и наконец, АС = АЕ. Точка С является искомой, она производит «золотое сечение» отрезка АВ. В самом деле, заметим, что по теореме Пифагора (AE + ED)2 = AB2 + BD2 а по построению АЕ = АС, ED = BD = Из этих равенств следует, что АС2 + АС АВ = АВ2, а отсюда легко получить равенство (1). ЗОЛОТОЕ СЕЧЕНИЕ (золотая пропорция, деление в крайнем и среднем отношении, гармоническое деление) деление отрезка AB на две части так, что большая его часть AC является средней пропорциональной между всем отрезком AB и меньшей его частью CB, то есть AB : AC = AC : BC. Алгебраическое нахождение золотого сечения отрезка AB = а сводится к решению уравнения a/x = х/( а—х) (где х = AC). Отношение х к а может быть также выражено приближённо дробями 2/3, 3/5, 5/8, 8/13, 13/21 и т.д., где 2, 3, 5, 8, 13, 21 и т.д. — Фибоначчи числа . Золотое сечение было известно ещё в древности. В дошедшей до нас античной литературе впервые встречается в «Началах» Евклида (3 век до н. э.). Термин «Золотое сечение» ввёл Леонардо да Винчи (конец 15 — начало 16 вв.). Принципы золотого сечения легли в основу композиционного построения многих произведений мирового искусства (главным образом произведений архитектуры античности и Возрождения). ФИБОНАЧЧИ ЧИСЛА, элементы числовой последовательности 1, 1, 2, 3, 5, 8,... (ряда Фибоначчи, Fibonacci; 1202), в которых каждый последующий член равен сумме двух предыдущих.  храм Афины Парфенос на Акрополе в Афинах, памятник древнегреческой высокой классики.Расположен напротив Эрехтейона, построил знаменитый архитектор Иктин. В храме стояла статуя Афины-Девы из золота и слоновой кости работы Фидия, в специальном хранилище храма хранились священные деньги богини и казна Афин и их союзников. Во фронтонах Парфенона, между скатами крыши, располагались скульптуры, изображавшие рождение Афины из головы Зевса и ее спор с морским богом Посейдоном за власть над Аттикой. Мраморный дорический периптер с ионическим скульптурным фризом (447-438 до н. э., архитекторы Иктин и Калликрат) замечателен величественной красотой форм и пропорций. Статуи фронтонов, рельефы метоп и фриза (окончены в 432 до н. э.) созданы под руководством Фидия. Разрушен в 1687; частично восстановлен. 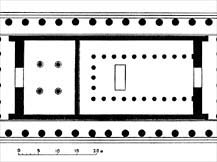 Парфенон, вид сверху, план здания.   Рисунки, фотографии, чертежи 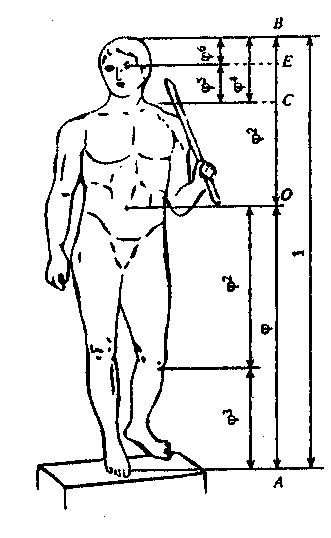 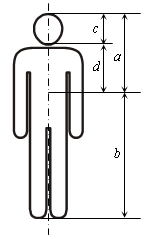   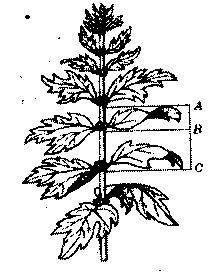  ФОТОГРАФИИ с. СЕЛА СЕЛЕЗЕНИХА КИРОВО- ЧЕПЕЦКОГО РАЙОНА , КИРОВСКОЙ ОБЛАСТИ 613037    Сельский совет Сельский совет  МОУ СОШ с. Селезениха МОУ СОШ с. СелезенихаМагазин.   дом музей Васнецовых. С. Рябово. 2002 год дом музей Васнецовых. С. Рябово. 2002 годздание старого медпункта, дом Домнина  ДЕТСКИЙ САД ЧЕБУРАШКА   церковь 1748 года церковь 1748 года |
