1.01 Механика. Зубакин Игорь Александрович отчет принят Рабочий протокол и отчет
 Скачать 65.45 Kb. Скачать 65.45 Kb.
|
Рабочий протокол и отчет по лабораторной работе № 1.01 Цель работы: Исследование распределения случайной величины на примере многократных измерений определённого интервала времени. Задачи, решаемые при выполнении работы: провести многократные измерения определенного интервала времени; построить гистограмму распределения результатов измерения; вычислить среднее значение и дисперсию полученной выборки; сравнить гистограмму с графиком функции Гаусса с такими же как и у экспериментального распределения средним значением и дисперсией. Объект исследования: Метод экспериментального исследования: сделать многократные измерения 5-секундного интервала времени; на основе этих данных сделать гистограмму распределения результатов измерения; вычислить среднее значение и дисперсию полученной выборки; Сравнить гистограмму с графиком функции Гаусса с такими же как и у экспериментального распределения средним значением и дисперсией. Рабочие формулы и исходные данные: Количество интервалов 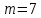 (Ближайшее целое число к квадратному корню количества измерений) (Ближайшее целое число к квадратному корню количества измерений)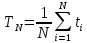 - среднеарифметическое всех измерений, где - среднеарифметическое всех измерений, где N – количество измерений ti – i-тое измерение 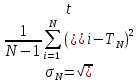 – среднеквадратичное отклонение – среднеквадратичное отклонение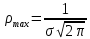 – максимальная плотность вероятности – максимальная плотность вероятности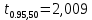 – коэффициент Стьюдента – коэффициент Стьюдента6. Измерительные приборы.
7. Схема установки (перечень схем, которые составляют Приложение 1). ---------------------- 8. Результаты прямых измерений и их обработки (таблицы, примеры расчетов).
9. Расчет результатов косвенных измерений (таблицы, примеры расчетов).
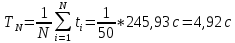 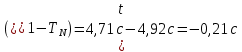 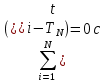 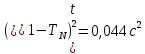 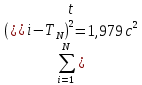 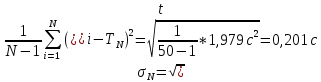 10. Расчет погрешностей измерений (для прямых и косвенных измерений). 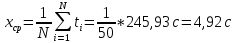 – среднеарифметическое значение измерений – среднеарифметическое значение измерений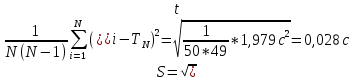 – среднеквадратическое отклонение измерений – среднеквадратическое отклонение измерений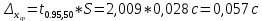 – доверительный интервал случайной погрешности – доверительный интервал случайной погрешности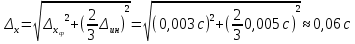 – абсолютная погрешность – абсолютная погрешность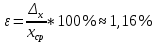 - относительная погрешность - относительная погрешность11. Графики (перечень графиков, которые составляют Приложение 2). Гистограмма с функцией плотности распределения. 12. Окончательные результаты. 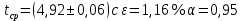 Распределение измерений по интервалам:
13. Выводы и анализ результатов работы. На примере многократных измерений определённого интервала времени мы построили гистограмму с функцией плотности распределения. По ней можно заметить, что функция плотности возрастает к 5 интервалу (4,87–5,03), а затем убывает. Из этого можно сделать вывод, что для многократных измерений некоторого определённого интервала времени случайная величина распределяется согласно нормальному распределению Гаусса. 14. Дополнительные задания. -------------------------- 15. Выполнение дополнительных заданий. --------------------------- 16. Замечания преподавателя (исправления, вызванные замечаниями преподавателя, также помещают в этот пункт). Приложение 2 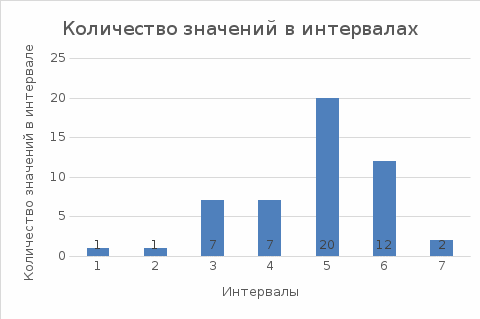 |

