Системы звездного и Всемирного времени. Звездного времени 7

• Название: Звездного времени 7
• Дата: 15.03.2023
• Размер: 0.52 Mb.
• Имя файла: Системы звездного и Всемирного времени.doc
• Тип: Реферат; #991685

Титульный лист

Содержание

Введение 3

1.Общее понятие об измерении времени 4

2.Система звездного времени 7

3.Система Всемирного времени 13

4.Перевычисление времени и наличие зависимостей 16

Заключение 20

Список использованных источников 21

Введение

Актуальность темы обусловлена тем, что определение координат небесных тел в определенный, т.е. заданный момент времени – это одна из задач геодезической астрономии и космической геодезии. Астрономическими шкалами времени и их построением сегодня занимаются национальные службы времени и Международное бюро времени.

Следует отметить, что в основе всех способов построения непрерывных шкал времени, которые известны на сегодняшний момент, лежат периодические процессы, такие как вращение Земли вокруг своей оси, обращение Земли вокруг Солнца по орбите; обращение Луны вокруг Земли по орбите; качание маятника под действием силы тяжести; упругие колебания кристалла кварца под действием переменного тока; электромагнитные колебания молекул и атомов; радиоактивный распад ядер атомов и другие процессы. Исходя из этих процессов, в геодезической астрономии, а также астрометрии и небесной механике используются системы звездного и солнечного времени. В основе систем – вращение Земли вокруг своей оси.

Цель исследования – провести анализ особенностей систем звездного и Всемирного времени.

Структура работы включает введение, основную часть, заключение, список использованных источников.

1. Общее понятие об измерении времени

Поскольку природа и человечество развивалось, жизнь и деятельность людей требовала некоторого измерения во времени. Основная единица измерения времени с давних пор – год. Год – это период времени полного обращения Земли вокруг Солнца.

Как всем известно, год делится на сутки, а сутки – это период времени полного оборота Земли вокруг своей оси. В свою очередь, сутки имеют деление на 24 части, которые называются часами (1 сутки = 24^h). Для того чтобы считать часы, были изобретены часы: солнечные, песочные, водяные, а позднее – механические.

С тех пор, как наука и техника на определенном этапе (XVIII в.) не смогли справиться с измерением часа с точностью, то возникли сначала минутная, а через 100 лет – секундная стрелки на часах. Возникло понятие «минуты» - период времени, равный 1/60 часа (1^h = 60^m), а позднее – понятие «секунды» - 1/60 части минуты (1^m = 60^s).

К концу XVIII в. был накоплен определенный опыт в точном измерении времени. Установлено, что вследствие неравномерного движения Земли по орбите вокруг Солнца продолжительность суток в течение года неодинакова (рис. 1).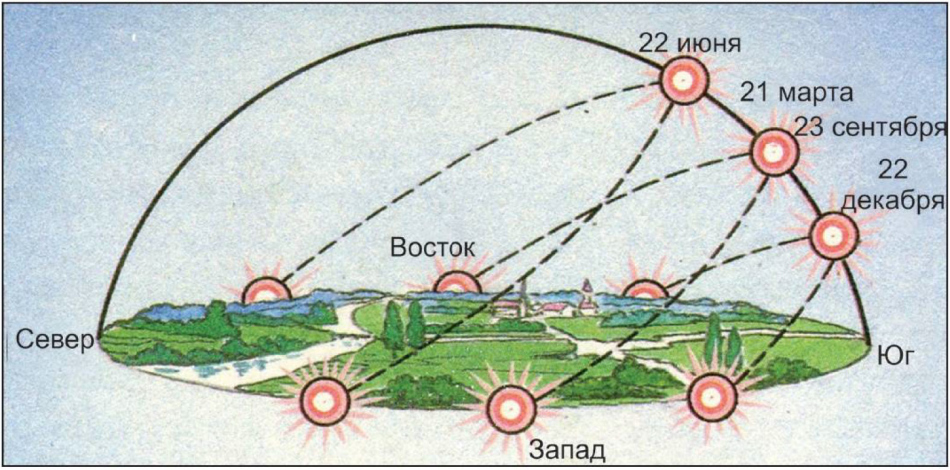


Рисунок 1 – Пояснение причин различной продолжительности суток в течение года

Так, в период, когда в северном полушарии зима, сутки короче, а когда лето – длиннее. Разность между ними достигает 15 сек. Неравномерная продолжительность суток происходит из того, что зимой расстояние от Земли до Солнца уменьшается (ввиду величины угла падения солнечных лучей на Землю), и Земля убыстряет свое движение. Летом же, наоборот, - с увеличением расстояния до Солнца движение Земли замедляется.

Для того, чтобы сделать сутки равными по длительности в течение всего года, были введены понятия «истинные солнечные сутки», «среднее Солнце» и «средние солнечные сутки». С позиции измерения периодов времени нет разницы в том, рассматриваем ли мы действительное вращение Земли вокруг своей оси или видимое нами суточное обращение Солнца по эклиптике, т.к. эти периоды равны. Точно также можно говорить о действительном движении Земли вокруг Солнца или о видимом нами годичном движении Солнца относительно звезд, т.к. эти периоды тоже равны.

В видимом суточном обращении Солнца оно дважды пересекает плоскость небесного меридиана (рис. 2), проходящий через пункт наблюдения.



Рис. 2. Видимое обращение Солнца
Прохождение Солнца или звезды через плоскость небесного меридиана называется кульминацией светила, а сами точки на небесной сфере – кульминационными. Ближайшая к зениту кульминационная точка называется верхней (полдень), а ближайшая к надиру – нижней (полночь). Истинные солнечные сутки – период времени между двумя последовательными нижними кульминациями центра диска Солнца. Такая единица времени практически сегодня не находит применения. В науке пользуются средними солнечными сутками. Для этого истинное Солнце заменяется средним экваториальным Солнцем, в качестве которого принимается условная точка, видимое годичное движение которой происходит равномерно, но не по эклиптике, а по небесному экватору.

В видимом суточном обращении среднее Солнце, как и истинное, дважды пересекает плоскость меридиана. Средние солнечные сутки, таким образом, - период времени между двумя последовательными нижними кульминациями среднего Солнца. Учитывая, что в каждой точке на земной поверхности проходит свой небесный меридиан, начало счета среднего солнечного времени в каждой точке будет свое. Такое время – местное среднее время.

2. Система звездного времени

В качестве основной единицы измерения времени принимается промежуток, в течение которого Земля совершает полный оборот вокруг своей оси, относительно вспомогательной точки небесной сферы. Вспомогательными точками могут являться: точка весеннего равноденствия (γ), центр видимого диска Солнца — истинное солнце и среднее экваториальное Солнце.

Звезды в своем видимом движении делают в течение уток полный оборот по небесным или суточным параллелям (окружностям qq1, параллельным небесному экватору). Вместе со звездами суточное движение совершает по небесной сфере и точка весеннего равноденствия, которая движется по небесному экватору (рис. 3).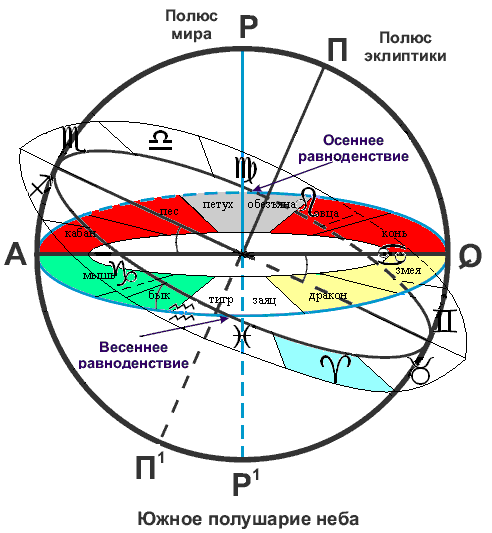


Рисунок 3 – Видимое суточное движение звезд и точки весеннего равноденствия
Период времени между двумя последовательными верхними кульминациями точки весеннего равноденствия называется звездными сутками. В каждом пункте наблюдения проходит свой меридиан и, следовательно, свое начало местных звездных суток и свое звездное время. Оно называется местным звездным временем и обозначается s. Звездное время на меридиане Гринвичской обсерватории называется Гринвичским звездным и временным и обозначается S.

Системы счета времени приведены в табл. 1.
Таблица 1 – Системы счета времени

Название времени и его обозначение	Начало отсчета	Единица измерения времени
Местное среднее время Tm	Момент нижней кульминации среднего Солнца (средняя полночь) на меридиане точки наблюдения	Средние сутки
Всемирное время То	Момент нижней кульминации среднего Солнца (средняя полночь) на меридиане Гринвичской обсерватории	Средние сутки
Постоянное время TN	для часового пояса номер N – средняя полночь на меридиане с долготой 15 N = Nh восточнее Гринвича	Средние сутки
Декретное время TN+1	Для часового пояса номер N – средняя полночь на меридиане с долготой 15 (N+1) = (N+1)h восточнее Гринвича	Средние сутки
Местное звездное время s	Момент верхней кульминации точки весеннего равноденствия на меридиане точки наблюдения	Звездные сутки
Гринвичское звездное время S	Момент верхней кульминации точки весеннего равноденствия на меридиане Гринвичской обсерватории	Звездные сутки

Началом измерения интервала времени служит момент кульминации вспомогательной точки небесной сферы на истинном астрономическом меридиане. Измерение интервала времени заключается в определении часового угла t вспомогательной точки небесной сферы, численно равного двугранному углу, заключенному между плоскостью истинного меридиана и кругом склонения вспомогательной точки (рис. 4).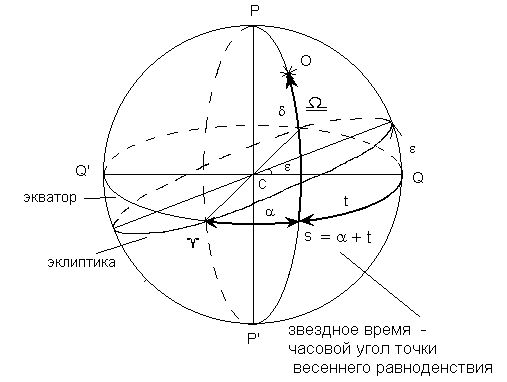



Рисунок 4 – Связь звездного времени с а и t светила
При создании системы звездного времени за вспомогательную точку небесной сферы принимается точка весеннего равноденствия — точка γ. В качестве единицы измерения используются звездные сутки — промежуток времени между двумя последовательными верхними кульминациями точки γ на меридиане места наблюдения. Звездные сутки равны 24 звездным часам. За начало отсчета принимается момент верхней кульминации точки γ. Интервал времени измеряется часовым углом точки γ:

s = tγ

(1)

Из рис. 4 видно, что часовой угол точки весеннего равноденствия равен:

tγ = s = α+t

(2)

В момент верхней кульминации светила t=0, тогда

s = α

(3)

В момент нижней кульминации светила t=12^h, и

s = α+12h

(4)

При измерении времени по Солнцу за точку, относительно которой отсчитываются обороты Земли вокруг оси, принимается центр солнечного диска, который обычно называют истинным Солнцем. Промежуток времени между двумя последовательными нижними кульминациями центра истинного Солнца на меридиане места наблюдения называется истинными солнечными сутками. Истинные солнечные сутки равны 24 истинным солнечным часам. За начало отсчета принимается истинная полночь - момент нижней кульминации центра диска истинного Солнца. Истинное солнечное время измеряется часовым углом центра Солнца t плюс 12^h:

m  = t+12h

(5)

Продолжительность истинных солнечных суток в течении года меняется вследствие неравномерной скорости движения Солнца по эклиптике, а также благодаря наклону последней к экватору.

Для устранения этих неудобств вводится понятие о среднем Солнце, т.е. о воображаемой точке, равномерно движущейся по экватору и завершающей по нему полный оборот за один тропический год. Тропический год - промежуток времени между двумя последовательными прохождениями истинного Солнца через точку весеннего равноденствия. Тропический год равен 365.2422 средним солнечным суткам. 

Средними солнечными сутками называется промежуток времени между двумя последовательными нижними кульминациями среднего экваториального Солнца на меридиане данного пункта. Средние солнечные сутки равны 24 средним солнечным часам. За начало средних солнечных суток принята средняя полночь — момент нижней кульминации среднего Солнца. Время, прошедшее от начала средних солнечных суток до любого другого момента, выраженное в средних солнечных часах, минутах и секундах, называется средним солнечным временем и обозначается буквой m. Среднее солнечное время численно равно часовому углу среднего экваториального Солнца t_ср. на данном меридиане, выраженному в часовой мере и увеличенному на 12^h:

m = tср.+12h

(6)

Звездное время s, истинное солнечное время m и среднее солнечное время m в любой точке земной поверхности называется соответственно местным звездным, местным истинным солнечным и местным средним солнечным временем этой точки.

В каждой точке земной поверхности считается свое местное время. В точках, расположенных на одном географическом меридиане, одноименное местное время, определенное в один и тот же физический момент, одинаково. Разность одноименных местных времен, определенных в один и тот же физический момент в двух пунктах А и В земной поверхности, расположенных на разных географических меридианах можно получить, воспользовавшись теоремой, устанавливающей связь между разностью долгот пунктов земной поверхности и разностью часовых углов светила, наблюденных в этих пунктах в один и тот же физический момент времени:

tA − tB=λA − λB

(7)

Применяя формулу (7) к часовым углам точек, используемых для измерения времени и, принимая во внимание формулы (2), (5) и (6), получим следующие формулы:

SA − SB=λA − λB mA − mB=λA − λB

(8)

Местное звездное время и местное истинное солнечное время данного меридиана получаем из астрономических наблюдений, произведенных на данном меридиане.

Годичное движение среднего Солнца по небесному экватору совершается навстречу суточному движению звезд. Вследствие этого суточное движение среднего Солнца оказывается медленнее суточного движения звезд и точки весеннего равноденствия. Постепенно это отставание накапливается и в течение года становится равным одной окружности, т.е. в течение тропического года число суточных оборотов точки весеннего равноденствия будет на единицу больше числа суточных оборотов среднего Солнца, т.е. тропический год будет равен 366,2422 звездных суток.

Из этого равноденствия выходят формулы для перевода звездного времени в среднее время, и обратно.

Обозначим через u = 1/365,2422 и через v = 1/366,2422. Тогда:
Т* = Т(1+u) = Т+Т*u; Т = Т*(1-v) = Т* - T* v (7)
где Т* - промежуток времени в звездных единицах;

Т – промежуток времени в средних единицах.

Таблицы для перевода звездного времени в среднее и обратно (с точностью до 0^s01) приводятся в Астрономическом ежегоднике и Каталоге координат Солнца и ярких звезд.

Пользуясь вышеприведенной формулой, можно определить, чему равны средние сутки в звездных единицах и чему равны сутки в средних единицах:

1 средние сутки = 24 (1+u) = 24^h03^m56^s, 56 звездных;

1 звездные сутки = 24 (1-v) = 23^h56^m04^s, 09 средних.

3. Система Всемирного времени

Всемирное время или UT (англ. Universal Time) — шкала времени, основанная на вращении Земли. Всемирное время является современной заменой среднего времени по Гринвичу (GMT), которое сейчас иногда некорректно используется в качестве синонима для всемирного координированного времени (UTC).

Всемирное время введено 1 января 1925 года. Фактически термин «всемирное время» является многозначным, так как существует несколько версий всемирного времени, главными из которых является UT1 и UTC (см. ниже). Все версии всемирного времени основаны на вращении Земли относительно далёких небесных объектов (звёзд и квазаров), используя коэффициент масштабирования и другие подстройки для того, чтобы быть ближе к солнечному времени.

Всемирное время UT - местное среднее солнечное время гринвичского ( =0) меридиана. Если долготу   места на Земле выражать в часовой мере и считать положительной к востоку от Гринвича, то имеет место следующее соотношение:
Тм = UT + λ (8).
Вследствие своего видимого годичного движения Солнца перемещается относительно звезд и относительно точки весеннего равноденствия навстречу суточному вращению небесной сферы, звездные сутки примерно на 4^m короче средних солнечных суток. По истечении полного года опоздание среднего экваториального Солнца будет равно 24 звездным часам, то есть одним звездным суткам

365,2422 средних солнечных суток = 366,2422 звездных суток,

Откуда 1 ср. солн. сутки = звездных суток

1 звезд. сутки =  сред. солн. суток.

Так как в 0^h среднего солнечного времени (в момент начала средних солнечных суток) звездное время не равно 0^h, то переход от среднего солнечного времени m к звездному s представим формулой:

s = s0+m+mμ,

(9)

где s₀ — звездное время в 0h среднего солнечного времени, т.е. в местную среднюю полночь:

s0 =S0±λμ

(10)

Значение S₀ — звездное время в среднюю гринвичскую полночь, т.е. в всемирного времени, приводится в АЕ в таблице "Звездное время" на каждый день года.

Для гринвичского меридиана запишем

S=S0+M+Mμ

(11)

где S — звездное гринвичское время, соответствующее данному моменту M;

S₀ — звездное время в среднюю гринвичскую полночь;

M — всемирное время;

Mμ — редукция всемирного времени в звездное.

Перевод местного звездного времени в среднее солнечное осуществляется по формуле:

m=(s−s0)−(s−s0)·ν,

(12)

где разность (s−s₀) представляет собой промежуток времени, прошедший от местной полуночи до заданного момента s, выраженный в звездных единицах времени;

(s−s₀)·ν — редукция за переход от звездных единиц времени к средним;

s₀ — звездное время в местную среднюю полночь, вычисляемое по формуле (10).

Для гринвичского меридиана запишем:

m=(S−S0)−(S−S0)·ν,

(13)

Применение системы местного солнечного времени приводит к тому, что на каждом меридиане с долготой λ будет свое местное время. В целях практического удобства земной шар разбили на 24 часовых пояса через каждые 15° по географической долготе с тем, чтобы внутри каждого пояса, имеющего номер n (n изменяется от 0 до 23), часы указывали одно и то же поясное время — время географического меридиана, проходящего через середину этого пояса. При переходе от пояса к поясу в направлении с запада на восток время на границе пояса скачком увеличивается ровно на один час.

4. Перевычисление времени и наличие зависимостей

Поскольку за начало местного звездного времени в точке наблюдения принимается момент верхней кульминации точки весеннего равноденствия в пункте наблюдения, то для определения значения местного звездного времени в какой-то другой момент времени достаточно было бы измерить часовой угол точки весеннего равноденствия в этот момент (рис. 5), т.к. s = t^y.

Однако выполнить это невозможно, поскольку точки весеннего равноденствия на небесной сфере реально не существует. При этом, зная часовой угол звезды t и ее прямое восхождение «a», можно вычислить местное звездное время в момент наблюдения по формуле:
s = t^y = t + a (14).
Если наблюдение звезды проводится в момент ее верхней кульминации, местное звездное время равно прямому восхождению звезды:
s = a (15).
Значение прямых восхождений звезд «а» указываются в Астрономическом ежегоднике. Зная местное звездное время s в точке наблюдения, по формулам (14) и (15), можно найти местное среднее время в этой точке.

Известно также, что долготы точек на земной поверхности отсчитываются от Гринвичского меридиана. Поэтому если из наблюдений звезды определено местное звездное время и на момент наблюдений звезды известно Гринвичское звездное время S, долгота пункта наблюдений будет равна:
λ = s - S (16),
где s – местное звездное время;

S – Гринвичское звездное время (рис. 6).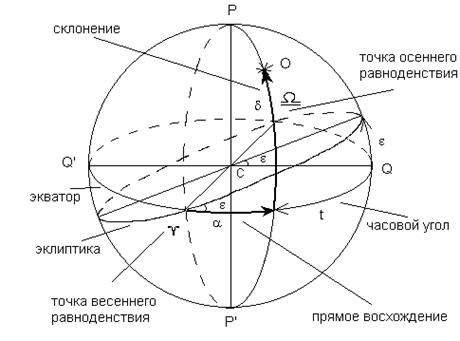



Рисунок 6 – Зависимость между местным звездным временем и часовым углом звезды
Гринвичское звездное время в момент наблюдения звезды вычисляется по отсчету, снятому с хронометра (часов), и результату последующей сверки хода хронометра (часов) со специальными радиосигналами времени, передаваемыми службами времени в установленные моменты по Гринвичскому среднему времени.

Общая схема решения задач на перевод времени из одной системы счета в другую заключается в определении промежутка времени между началами отсчета. Если системы счета времени однородны, т.е. в двух пунктах наблюдения А и В известно звездное или среднее время, задачи на перевод времени решаются довольно просто (необходимо только знать долготы этих пунктов):
S_A = S_B + (λ_A – λ_B);

T_mA = T_mB + (λ_A – λ_B) (17).
Если системы счета времени разные, т.е. в одном пункте известно звездное время, а в другом – среднее, для перевода времени необходимо знать дату наблюдения, значение долгот пунктов и иметь Астрономический ежегодник.

Рассмотрим примеры.

Пример 1. Найти всемирное время (время на меридиане Гринвичской обсерватории), если московское время 17^h42^m16^s.

Решение:

Т₀ = Т_N+1 – (N + 1)^h = 17^h42^m16^s – 3^h = 14^h42^m16^s.
Пример 2. Найти местное среднее время в пункте наблюдения с восточной долготой λ = 28⁰30^'00^” для момента наблюдения 19^h17^m24^s декретного времени.

Решение:

- находится Всемирное время Т₀, соответствующее моменту наблюдения:

Т₀ = Т_N+1 – (N + 1)^h = 19^h19^m24^s – 3^h = 16^h17^m24^s;

- долгота пункта выражается в часовой мере [каталог координат Солнца и ярких звезд (Каталог), с. 195]:
λ = 28⁰30^'00^{” =} 1^h54^m00^s;

- местное среднее время Т_m равно:

Т_m = T₀ = λ^h = 16^h17^m24^s + 1^h54^m00^s = 18^h11^m24^s.
Пример 3. Найти местное звездное время в пункте с восточной долготой λ=28^о30'00”, если в момент наблюдения 23 сентября 2001 г. по московскому времени было 21^h31^m30^s.

Решение:

- находится Всемирное время Т₀, соответствующее заданному моменту T_N+1 декретного времени пояса № 2:

Т₀ = Т_N+1 – (N + 1)^h = 21^h31^m30^s – 3^h = 18^h31^m30^s;

- выписывается Гринвичское звездное время в 0^h Всемирного времени 23 сентября 2001 г. (Каталог, с.14):

S_o = 0^h04^m45^s,7;

- промежуток среднего времени от 0^h до Т₀ = 18^h31^m30^s переводится в звездное время (Каталог, с. 192):

Т₀ + Т_0u = 18^h31^m30^s + 03^m02^s,59 = 18^h34^m32^s,59;

- Гринвичское звездное время S, соответствующее моменту наблюдения московского времени (пояса № 2), будет:

S=S_o+T_o+ Т_0u= 0^h04^m45^s,70 + 18^h34^m32^s,59 = 18^h39^m18^s,29;

- местное звездное время в пункте наблюдения будет равно:

s = S+λ= 18^h39^m18^s,29 + 1^h54^m00^s= 20^h33^m18^s,3.

Заключение

Итак, можно утверждать, что единицей измерения времени в астрономии служат сутки - промежуток времени, в течение которого Земля делает полный оборот вокруг своей оси относительно какой-нибудь точки на небе.

Солнечные сутки примерно на 4 минуты длиннее звездных, так как Солнце двигается среди звезд в сторону вращения Земли, и для того, чтобы его догнать, Земле надо сделать относительно звезд чуть больше одного оборота. Для измерения больших промежутков времени используют тропический год - промежуток времени между двумя последовательными прохождениями центра Солнца через точку весеннего равноденствия.

Для измерения времени можно использовать как звездные, так и истинные солнечные сутки. Если используются звездные сутки, измеряемое время называют звездным временем, а если истинные солнечные сутки - то истинным солнечным временем. Однако это не означает, что мы измеряем два каких-то независимых друг от друга времени. Фактически, это как бы две разные линейки для измерения времени. Так, расстояние между городами можно выразить и в километрах, и в милях. Ситуация с измерением времени та же самая.

Система звездного времени применяется при определении географических координат пунктов на поверхности Земли и азимутов направления на земные предметы, при изучении неравномерностей суточного вращения Земли, при установлении нульпунктов шкал других систем измерения времени. Эта система, хоть и широко применяется в астрономии, в повседневной жизни неудобна. Смена дня и ночи, обусловленная видимым суточным движением Солнца, создает вполне определенный цикл в деятельности человека на Земле. Поэтому издавна счисление времени ведется по суточному движению Солнца.

Список использованных источников

1. 
   Буденков Н.А. Геодезия с основами землеустройства. – Йошкар-Ола: Марийский государственный технические университета, Поволжский государственный технологический университета, 2009. – 184 с.
   
2. 
   Дударев В.И. Классификация систем координат, применяемых в космической геодезии // Интерэкспо Гео-Сибирь, 2010. - № 7. – С.13-17.
   
3. 
   Золотова Е.В. Геодезия с основами кадастра. – М.: Академический проект: Фонд «Мир», 2012. – 413 с.
   
4. 
   Куштин И.Ф., Куштин В.И. Геодезия. – Ростов-на-Дону: Феникс, 2009. – 909 с.
   
5. 
   Орехов М.М. Автоматизированная обработка инженерно-геодезических изысканий в программном комплексе CREDO. – СПБ.: Санкт-Петербургский государственный архитектурно-строительный университет, 2013. – 42 с.
   
6. 
   Пандул И.С. Геодезическая астрономия применительно к решению инженерно-геодезических задач. – СПб.: Политехника, 2011. – 324 с.
   
7. 
   Полежаева Е.Ю. Геодезия с основами кадастра и землепользования. – Самара: Самарский государственный архитектурно-строительный университет, 2009. – 260 с.