отчет 19 вар. 1 оптимизация плана выпуска продукции при ограниченных ресурсах
 Скачать 246.41 Kb. Скачать 246.41 Kb.
|
|
Титульный лист 19 вариант 1 ОПТИМИЗАЦИЯ ПЛАНА ВЫПУСКА ПРОДУКЦИИ ПРИ ОГРАНИЧЕННЫХ РЕСУРСАХЗадание 1 Мебельная фабрика выпускает два вида изделий: шкафы и столы. В производстве применяется оборудование трех типов: фрезерные, сверлильные и шлифовальные станки. Нормы времени работы каждого вида оборудования в час, необходимые для изготовления одного изделия каждого вида, а также ресурсы рабочего времени для каждого вида оборудования, известны и приведены в табл. 1.1. Таблица 1.1
Фабрика получает прибыль от изготовления и реализации одного шкафа в размере 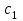 ден.ед. и одного стола – в размере ден.ед. и одного стола – в размере  ден.ед. Цена за простой 1 часа оборудования ден.ед. Цена за простой 1 часа оборудования 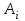 составляет составляет  ден.ед., ден.ед., 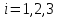 . Эти данные содержатся в таблице. . Эти данные содержатся в таблице.Требуется определить план выпуска изделий каждого вида, при котором время работы оборудования не превышало бы допустимого фонда времени, и при этом во-первых, была получена наибольшая общая прибыль; во-вторых, был получен минимальный штраф за простой оборудования; в третьих, была получена наибольшая общая прибыль с учетом штрафа за простой оборудования. Выполнение Пусть x1 и x2 – количество шкафов и столов, которые необходимо изготовить на предприятии, пусть z – общая прибыль от реализации готовой продукции, w – суммарные издержки (штраф) предприятия за простой оборудования, F = z – w – общая прибыль от реализации готовой продукции за вычетом штрафа предприятия за простой оборудования. 1.1 Математическая модель максимизации прибыли Фактическая загрузка по каждой группе оборудования равна: 14x1 + 18x2 – для строгальных станков, 14x1 + 20x2 – для фрезерных станков, 20x1 + 0x2 – для шлифовальных станков. Коэффициенты при неизвестных обозначают здесь нормы затрат машинного времени на обработку одного шкафа и одного стола. Загрузка по каждой группе оборудования не должна превышать фонда машинного времени, т.е.:  Неизвестные, очевидно, должны быть неотрицательными: 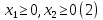 Неравенства (1) и (2) образуют систему ограничений. Общая прибыль от реализации готовой продукции (цель 1) выражается формулой  (3) (3)Таким образом, математическая модель задачи по критерию максимальной прибыли состоит в определении чисел 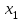 и и  , удовлетворяющих системе ограничений (1) - (2), для которых значение функции (3) будет максимальным. Это есть задача линейной оптимизации. , удовлетворяющих системе ограничений (1) - (2), для которых значение функции (3) будет максимальным. Это есть задача линейной оптимизации.1.2 Математическая модель минимизации штрафа Составим математическую модель для второго критерия. Из ограничений следует, что время простоя станков равно: 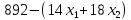 – для строгальных станков, – для строгальных станков,  – для фрезерных станков, – для фрезерных станков,  – для шлифовальных станков, – для шлифовальных станков, поэтому суммарные издержки предприятия за простой оборудования (цель 2) составляют: 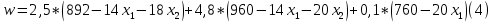 или  (5) (5)Таким образом, математическая модель задачи по второму критерию состоит в минимизации целевой функции (5) при условиях, что неизвестные 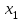 и и  удовлетворяют системе ограничений (1) и неравенствам (2). Это также есть задача линейной оптимизации. удовлетворяют системе ограничений (1) и неравенствам (2). Это также есть задача линейной оптимизации.1.3 Графическое решение задачи максимизации прибыли На рис. 1 приведено графическое решение задачи по критерию (3). На основе системы ограничений (1) – (2) строится допустимая область в виде многоугольника OABCD. Покажем, например, как построена прямая I. В уравнении  положим положим  тогда получим тогда получим 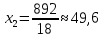 . Затем положим . Затем положим  тогда тогда 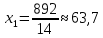 . Через две точки проведем прямую I. Неравенство . Через две точки проведем прямую I. Неравенство 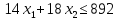 определяет полуплоскость, расположенную ниже этой прямой. Аналогично неравенство определяет полуплоскость, расположенную ниже этой прямой. Аналогично неравенство 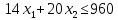 задает полуплоскость, расположенную под прямой II, а неравенство задает полуплоскость, расположенную под прямой II, а неравенство 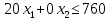 – полуплоскость, расположенную левее прямой III. Условия неотрицательности (2) в совокупности определяют первый квадрант координатной плоскости. – полуплоскость, расположенную левее прямой III. Условия неотрицательности (2) в совокупности определяют первый квадрант координатной плоскости. Оптимальное решение задачи по первому критерию определяется следующим образом. Строится вектор p1(40;25), координаты которого равны (или пропорциональны) коэффициентам целевой функции (3). Перпендикулярно этому вектору изображается прямая (линия уровня целевой функции), которая перемещается в направлении вектора, пока прямая имеет общие точки с допустимой областью. Оптимальное решение по первому критерию есть точка пересечения допустимой области с линией уровня, отвечающей максимальному значению  . Это есть вершина . Это есть вершина  . Координаты точки C(38;20) определяются по графику приближенно. Они дают оптимальное решение задачи по первому критерию. . Координаты точки C(38;20) определяются по графику приближенно. Они дают оптимальное решение задачи по первому критерию.   x1 x2  Рис. 1. Графическое решение задачи по первому критерию Таблица 1
Таким образом, выпуск продукции в количествах 38 и 20 ед. соответственно обеспечивает предприятию максимальную общую прибыль. Построение допустимой области можно выполнить в Excel. Для этого в соответствии с уравнениями системы (1) образуем табл. 1. В ячейках введем формулы из табл. 2. Таблица 2
С помощью мастера диаграмм и блока ячеек из табл. 1 строятся графики прямых линий I, II и III. Используя пункт меню «Ряд» и «Подписи оси x», указывают значения аргумента 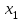 , содержащиеся в блоке ячеек. После построения прямых следует выделить допустимую область, ограничив диаграмму снизу и сверху по вертикальной оси. Путем изменения размеров графика необходимо добиться, чтобы масштаб по осям координат был одинаковым. Подписи данных удобно сделать, используя пункт меню «Вид / Панели инструментов / Рисование». , содержащиеся в блоке ячеек. После построения прямых следует выделить допустимую область, ограничив диаграмму снизу и сверху по вертикальной оси. Путем изменения размеров графика необходимо добиться, чтобы масштаб по осям координат был одинаковым. Подписи данных удобно сделать, используя пункт меню «Вид / Панели инструментов / Рисование». 1.4 Оптимизация общей прибыли в Excel Решение задачи по первому критерию получим теперь в Excel. Организация данных для решения задачи по первому критерию представлена в табл. 3. Таблица 3
Вначале ячейки B4:C4 – пустые, они предназначены для записи решения задачи. В ячейке D7 записана формула = СУММПРОИЗВ(B7:C7; $B$4:$C$4). Содержимое ячеек D8, D9, D11 получено копированием формулы из D7. В ячейке G10 записана формула = СУММПРОИЗВ(G7:G9; F7:F9 – D7:D9), характеризующая суммарный штраф за простой оборудования, как это следует из формулы (4). Далее идет обращение к процедуре «Поиск решения» в пункте меню «Сервис». Целевой ячейкой является D11. Оптимальный план выпуска продукции в количествах 38 и 20 ед. содержится в ячейках B4:C4, максимальная прибыль (ячейка D11) равна zmax = 2020 ден.ед. Штраф за простой оборудования составляет w = 134,4 ден.ед. 1.5 Оптимизация штрафа в Excel Решение задачи по второму критерию выполняется в Excel на другом листе аналогично (см. табл. 4), но целевой ячейкой служит G10. Таблица 4
Оптимальное решение по второму критерию (ячейки B4:C4) состоит в выпуске шкафов и столов в количествах 20 и 34 ед., минимальный штраф за простой оборудования (ячейка G10) составляет wmin=36 ден.ед., При этом прибыль (ячейка D11) равна z = 1650 ден.ед. Полученные результаты оптимизации по двум критериям сведены в табл. 5. Таблица 5
На рис. 1 оптимальному плану по прибыли соответствует вершина C(38;20), а оптимальному плану по штрафу – вершина C(20;34). 1.6 Математическая модель оптимизации прибыли с учетом штрафа Обратимся к третьему критерию оптимальности, равному разности общей прибыли предприятия от реализации готовой продукции и штрафа за простой оборудования. Математически задача состоит в максимизации функции 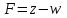 (6) (6)при ограничениях (1) - (2). Используя соотношения (3) и (5), получим  Тогда модель задачи состоит в определении чисел 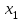 и и  , удовлетворяющих системе ограничений (1) - (2), для которых целевая функция , удовлетворяющих системе ограничений (1) - (2), для которых целевая функция 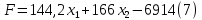 достигает максимума. Решение этой задачи выполним в Excel на третьем листе, как показано в табл. 6. Целевой ячейкой является G11, содержимое которой определяется формулой = D11 – G10, вытекающей из (6). Таблица 6
Поиск решения дает оптимальное решение по третьему критерию (ячейки B4:C4), которое состоит в выпуске шкафов и столов в количествах 38 и 20 ед. Максимальная прибыль с учетом штрафа за простой оборудования (ячейка G11) равна F = 1885,6 ден.ед. 1.7 Оптимизация штрафа в Excel Решение задачи по второму критерию выполняется в Excel на другом листе аналогично (см. табл. 7), но целевой ячейкой служит G10. Таблица 7
Оптимальное решение по второму критерию (ячейки B4:C4) состоит в выпуске шкафов и столов в количествах 20 и 34 ед., минимальный штраф за простой оборудования (ячейка G10) составляет wmin = 36 ден.ед., При этом прибыль (ячейка D11) равна F = 1614 ден.ед., z = 1650 ден.ед. Полученные результаты оптимизации по двум критериям сведены в табл. 8. Таблица 8
На рис. 1 оптимальному плану по прибыли соответствует вершина C(38;20), а оптимальному плану по штрафу – вершина C(20;34). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

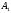 (фрезерные станки)
(фрезерные станки) (сверлильные станки)
(сверлильные станки)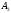 (шлифовальные станки)
(шлифовальные станки)