шпоры ильин. 1. Предмет и задачи дисциплины. Классификация осн процессов теплотехнологий

• Название: 1. Предмет и задачи дисциплины. Классификация осн процессов теплотехнологий
• Анкор: шпоры ильин
• Дата: 09.03.2022
• Размер: 1.26 Mb.
• Имя файла: shpory_ilin.docx
• Тип: Задача; #387972
• страница: 1 из 3

1. Предмет и задачи дисциплины. Классификация осн процессов теплотехнологий.

Основная задача дисциплины: выявление общих закономерностей процессов переноса и сохранения различных субстанций; разработка методов расчета технологических процессов.

Классификация основных процессов технологии

В зависимости от законов, определяющих скорость протекания процессов, они могут быть объединены в следующие группы:

1. Гидромеханические - скорость которых определяется законами гидромеханики. Сюда относятся транспортировка жидкостей и газов, получение и разделение неоднородных систем и др.

2. Тепловые - скорость которых определяется законами переноса теплоты (охлаждение и нагревание жидкостей и газов, конденсаций паров, кипение жидкостей и др.).

3. Массообменные - скорость которых определяется законами переноса массы из одной фазы в другую через поверхность раздела фаз (абсорбция, адсорбция, экстракция, перегонка жидкостей, сушка и т.д.).

4. Химические - скорость которых определяется законами химической кинетики.

5. Механические - которые описываются законами механики твердых тел (измельчение, сортировка, смешение твердых материалов и др.)

В курсе «Гидравлика теплотехнологий» изучается первые три группы.

В зависимости от того, как изменяются или не изменяются во времени параметры процессов (скорость движения потока, температура, давление и т.д.) их подразделяют на стационарные (установившиеся) и нестационарные (неустановившиеся).

Обозначим параметры как U, тогда:

- стационарные процессы, U(x,y,z)

- нестационарные, U(x,y,z,t)

Периодический процесс характеризуется единством места проведения отдельных его стадий. Процесс нестационарный.

Непрерывный процесс характеризуется единством времени протекания всех его стадий. Процесс установившийся (стационарный).

Встречаются комбинированные процессы – отдельные стадии проводятся непрерывно, отдельные – периодически.

2. Гипотеза сплошности среды. Режимы движения жидких сред.

Жидкая среда заполняет тот или иной объем без каких-либо промежутков, сплошным образом. Жидкая среда, благодаря изменению расстояния между частицами, меняет внешнюю конфигурацию, т.е. деформируется. Для твердого тела подвижность частиц мала, а для жидких сред – велика. Поэтому, мерой подвижности частиц для жидких сред служат уже не сами смещения, а скорость смещения частиц, т.е. скорости деформаций. Следовательно, для сплошной жидкой среды мерами подвижности частиц служат их скорости и их скорости деформации. Замкнутая поверхность, состоящая из одних и тех же частиц, будет непрерывно деформироваться. Если нет разрыва сплошной среды, то реализуется непрерывность распределения в объеме скоростей и плотностей частиц.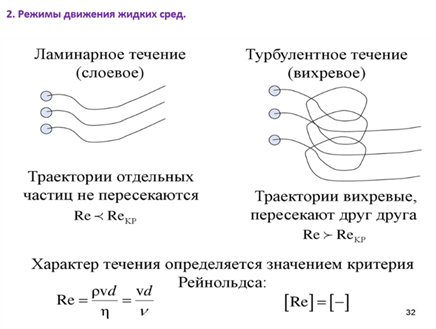



3. Силы и напряжения, действующих в жидких средах

Силы, действующие в жидкости, делятся на поверхностные и массовые.

Поверхностные силы действуют на поверхностях отделяющий данный объем от окружающей среды. Поверхностные силы могут быть нормальные (сжимающие и растягивающие), касательные (рис. 1.) и поверхностного натяжения. Сопротивлением жидкости, растягивающим силам можно пренебречь. Поверхностные силы непрерывно распределены по поверхности.





Гидростатическое давление в точке одинаково по всем направлениям и зависит только от положения точки внутри жидкости, т.е. p = f (x,y,z).

Для случая гидродинамики давление в точке определяется так:

, где p_{1, 2, 3} – главные нормальные напряжения в точке.

Отношение касательной силы к величине площади, на которую эта сила действуют, называется касательным напряжением:



Сила поверхностного натяжения.

На межфазной поверхности жидкости существует тонкий слой, в котором возникает натяжение, т.к. молекулы жидкости, находящиеся на поверхности сильнее притягиваются молекулами внутренних слоев, чем молекулами другой фазы на межфазной поверхности. Действие сил поверхностного натяжения проявляется в стремлении жидкости уменьшить свою поверхность. На создание новой поверхности F необходимо затратить некоторую работу A. Величина работы A, которую нужно затратить для образования единицы новой поверхности жидкости при постоянной температуре, называется коэффициентом поверхностного натяжения:

Вследствие поверхностного натяжения на любой искривленной межфазной поверхности жидкости возникает давление. Величина этого давления определяется формулой Лапласа:

Массовые силы действуют на каждую частицу данного объема жидкости. К ним относятся: сила тяжести, центробежная сила, сила инерции и сила Кориолиса:

сила тяжести Pт = Mg,

сила инерции Pин = Ma,

центробежная сила Pцб = Mω² r,

сила Кориолиса Pкор. = 2Mωw_отн

где M – масса, g – ускорение силы тяжести, ω - угловая скорость вращения, a–ускорение, wотн – относительная скорость, r – радиус вращения.

4. Дифференциальное уравнение гидростатики. Основное уравнение гидростатики

В гидростатике рассматриваются условия (законы) равновесия покоящейся жидкости. Поскольку жидкость находится в состоянии покоя, в ней не проявляются силы вязкого трения. В покоящейся жидкости действуют массовые и поверхностные силы.

Ранее из уравнения Навье – Стокса (как частный случай) было получено уравнение равновесия Эйлера

Распишем это уравнение по осям в декартовой системе координат:

где X, Y, Z – проекции единичных массовых сил по осям x, y, z; – градиенты давлений по направлениям осей x, y, z. Преобразуем систему уравнений . Для этого первое уравнение системы умножим на dx, второе – на dy, третье – на dz и, сложив эти три уравнения, получим:

Правая часть полученного уравнения представляет собой полный дифференциал давления. Следовательно, можно записать:

Уравнение (1) называется основным дифференциальным уравнением гидростатики

Основное уравнение гидростатики можно получить разными способами:

– используя уравнение Бернулли, записанное для свободной поверхности и для поверхности, проходящей через точку А;

– используя основное дифференциальное уравнение гидростатики (1):

Рис. 1. Сосуд, заполненный жидкостью

В нашем случае действуют только силы тяжести. Поэтому Следовательно, имеем:

Запишем граничное условие: при . Проинтегрировав уравнение (2), получим:

Константа интегрирования определяется из граничного условия Итак, имеем Для точки А при получим:

Полученное уравнение (3) называется основным уравнением гидростатики.

5. Абсолютное и избыточное давление, вакуум, приборы для их измерения

Абсолютное - это то давление, для указания которого используется, в качестве точки отсчета, абсолютный вакуум.

Если абсолютное давление больше атмосферного – избыточное, если меньше – вакуум.

Избыточное давление - это то давление, для указания которого используется, в качестве точки отсчета, нормальное атмосферное давление.

Когда рабс>ратм, рабс=ратм+ризб, если давление на свободной поверхности ро=ратм, то весовое давление

Когда рабс<ратм. рабс=ратм-рвак, если давление в жидкости меньше атмосферного то состояние жидкости характеризуется разрежением (вакуумом).

Атмосферное давление - это давление, имеющееся в какой-либо точке измерения на Земле

Шкалы абс и изб. Давлений являются неограниченными, шкала ваккуума- ограничена, она меняется от атмосферного до нуля (вакуум ограничен объемом).

Для измерения гидростатического давления используют жидкостные и механические приборы. Пьезометр – жидкостный прибор, открытая с 2х концов стеклянная трубка, которая 1 концом присоединяется к источнику давления. 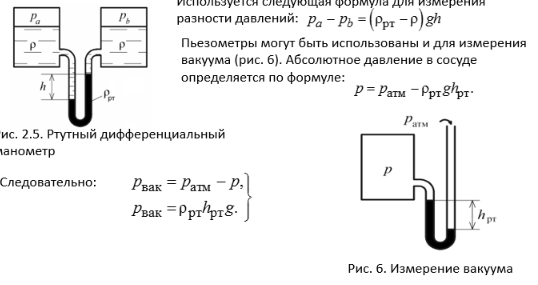, где hп-пьезометрическая высота, уровень жидкости от поверхности воды в сосуде, до поверхности воды в трубке. Их используют для низких давлений, для высоких – ртутные манометры. . Вместо ртути могут быть другие жидкости, плотность которых выше плотности жидкости. Для измерения перепада давления применяются жидкостные дифманометры.



Механические приборы используются в тех случаях, когда более точные, жидкостные, не могут применяться из-за чрезмерно больших измеряемых давлений. В некоторых конструкциях механических манометров и вакуумметров используются упругие рабочие элементы (например, полые пружины, гибкие диафрагмы, сильфоны и т.п.), которые деформируются под действием давления жидкости.
6. Закон Паскаля и его использование в технике

Внешнее давление, производимое на свободную поверхность покоящейся жидкости передается одинаково всем ее точкам по всем направлениям.

Согласно основному уравнению гидростатики , изменение внешнего давления на некоторую величину приводит к изменению давления во всех точках жидкости на ту же величину, - закон Паскаля, который используется в технике для умножения усилия и давления.

Умножение усилия.(поршень,пресс, 2 сосуда разных диаметров)

Если. Следовательно в подпоршневом пространстве реализуется постоянное давление. Один из сосудов имеет площадь, которая меньше площади второго сосуда. Если к поршню в сосуде 1 приложить силу, то под ним создаётся гидростатическое давление, определяемое по формуле.р=F\S, это давление передается на поршень большего диаметра.

По закону Паскаля давление передаётся во все точки жидкости, в том числе и на площадь. Это создаёт силу . Следовательно Р2=РS=H1(d2\d1)^2.

Таким образом, сила во столько раз больше другой силы, действующей на поршень в малом сечении, во сколько раз площадь больше другой площади.

Умножение давления (мультипликатор,домкрат 1 сосуд, вверху меньший диаметр, внизу больший) Сила, действующая на жесткую систему цилиндров равна , Таким образом, при помощи мультипликатора давление на выходе повышается в сколь угодно раз.

7. Сила давления жидкости на плоские стенки

Сначала рассмотрим силы давления жидкости на горизонтальные стенки.

Сила давления жидкости на горизонтальное дно сосуда определяется по формуле (рис. 1):

Pдн=рдн*S

а давление на дно, согласно основному уравнению гидростатики, как:рдн=p0+ρgh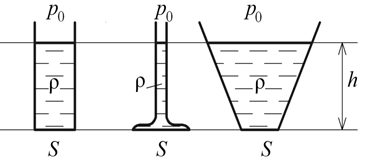


Следовательно, сила давления жидкости на горизонтальное дно зависит от

• 
  давления на свободной поверхности p0
  
• 
  плотности жидкости ρ
  

- глубины погружения поверхности h

но не зависит от формы сосуда (гидростатический парадокс).

Рассмотрим более общий случай. Пусть площадь расположена под углом к горизонту и перпендикулярна к плоскости рисунка (рис.2).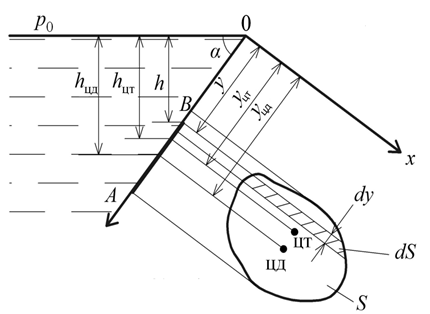



Через проекцию контура площади S (линия АВ) проведем ось оу и спроектируем эту площадь на плоскость хоу. Определим силу давления жидкости на элементарную площадку предполагая, что в пределах dy давление не меняется: dP=pdS=(po+ρgh)dS=p0dS+ρghdS

Последний интеграл в правой части уравнения представляет собой статический момент площади S относительно оси ох и равен:∫_S (ydS)=yцт*S

где yцт – координата центра тяжести площади S . Заменяя yцт*sin⁡α=hцт получим:P=(p0+ρghцт)S=pцт*S

Здесь pцт – давление в центре тяжести площади S. Полная сила давления на плоскую 5стенку равна произведению площади стенки на гидростатическое давление в центре тяжести этой площади.

Формулу (1) представим в другом виде: P=p0*S+ρghцт*S=P0+Pизб

Здесь P0 – внешняя сила, Pизб – избыточная сила, вызванная весом жидкости.

Внешнее давление p0 передается всем точкам площади S одинаково, поэтому внешняя сила P0 будет приложена в центре тяжести площади S. Сила избыточного давления Pизб из-за неравномерности распределения избыточного давления по глубине приложена ниже в центре давления hцд .

yцд=Iх/yцт*S

где Iх – момент инерции фигуры относительно оси ох.

Зависимость (2) может быть представлена в виде: yцд=yцт+ Iцт/yцт*S

где Iцт – момент инерции фигуры S относительно оси, проходящей через её центр тяжести. Величина Iцт/yцт*S представляет собой эксцентриситет.

Зная величины P0 и Pизб и точки их приложения, можно найти величину и точку приложения общей силы P.

8. Сила давления жидкости на криволинейные стенки.

В отличие от плоской стенки, элементарные силы, действующие на элементарные площадки криволинейной стенки в различных точках, различаются не только по величине, но и по направлению. Поэтому силу гидростатического давления, действующего на криволинейную стенку, непосредственно определить невозможно, его находят через составляющие (проекции) этой силы.

Для простоты рассмотрим цилиндрическую поверхность аb с образующей, перпендикулярной к плоскости чертежа (рис. 3). Жидкость действует на стенку аb с силой P , а стенка аb с такой же силой, но в обратную сторону. Разложим эту силу P на вертикальную Pz и горизонтальную Px составляющие.
Далее рассмотрим условие равновесия объема жидкости, заключенного в вертикальном направлении в отсеке abcd: Pz=P0+G=p0*Sz+ρgV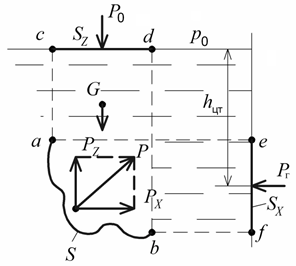



где p0 – давление на свободной поверхности, Sz – проекция площади S на горизонтальную (свободную) поверхность, V – объем жидкого тела. Объем жидкого тела (тело давления) ограничено снизу криволинейной поверхностью аb, сверху – проекцией этой поверхности на свободную поверхность cd, а с боков – цилиндрической поверхностью, полученной в результате проектирования площади S на свободную поверхность.
Необходимо отметить, что V не всегда представляет объем жидкости.
Определим горизонтальную составляющую Px . На некотором расстоянии по горизонтали от площади S жидкость условно разрезаем в вертикальной плоскости и правую часть отбрасываем. На вертикальную стенку спроектируем площадь S и получим Sx .

Реакцию отброшенной части жидкости обозначим через Pг . Далее рассмотрим равновесие объема жидкости, заключенной между плоскостями аb и ef. Заметим, что сила Pг является силой давления на плоскую стенку: