1. Предмет теории вероятности. Вероятность и статистика.
Теория вероятности и математическая статистика – это наука, занимающаяся изучением закономерностей массовых случайных явлений, то есть статистических
закономерностей. Такие же закономерности, только в более узкой предметнойобласти социально-экономических явлений, изучает статистика. Между этими науками имеется общность методологии и высокая степень взаимосвязи. Практическилюбые выводы сделанные статистикой рассматриваются как вероятностные.
Особенно наглядно вероятностный характер статистических исследований проявляется в выборочном методе, поскольку любой вывод сделанный по
результатам выборки оценивается с заданной вероятностью.С развитием рынка постепенно сращивается вероятность и статистика, особенно наглядно это проявляется в управлении рисками, товарными запасами, портфелем ценных бумаг и т.п. За рубежом теория вероятности и математическая статистика
применятся очень широко. В нашей стране пока широко применяется в управлении качеством продукции, поэтому распространение и внедрение в практику методов
теории вероятности актуальная задача.
2.Понятие события. Классификация событий.
Одним из основных понятий теории вероятностей является понятие события. Под событием понимают любой факт, который может произойти в результате опыта или испытания. Под опытом, или испытанием, понимается осуществление определённого комплекса условий.Примеры событий:
– попадание в цель при выстреле из орудия (опыт — произведение выстрела; событие попадание в цель);
– выпадение двух гербов при трёхкратном бросании монеты (опыт — трёхкратное бросание монеты; событие - выпадение двух гербов);
– появление ошибки измерения в заданных пределах при измерении дальности до цели (опыт - измерение дальности; событие — ошибка измерения).Можно привести бесчисленное множество подобных примеров. События обозначаются заглавными буквами латинского алфавита 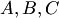 и т д.Различают события совместные и несовместные. События называются совместными, если наступление одного из них не исключает наступления другого. В противном случае события называются несовместными. Например, подбрасываются две игральные кости. Событие и т д.Различают события совместные и несовместные. События называются совместными, если наступление одного из них не исключает наступления другого. В противном случае события называются несовместными. Например, подбрасываются две игральные кости. Событие 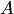 — выпадание трех очков на первой игральной кости, событие — выпадание трех очков на первой игральной кости, событие 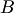 — выпадание трех очков на второй кости. — выпадание трех очков на второй кости. 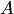 и и 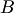 — совместные события. Пусть в магазин поступила партия обуви одного фасона и размера, но разного цвета. Событие — совместные события. Пусть в магазин поступила партия обуви одного фасона и размера, но разного цвета. Событие 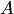 — наудачу взятая коробка окажется с обувью черного цвета, событие — наудачу взятая коробка окажется с обувью черного цвета, событие 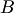 — коробка окажется с обувью коричневого цвета, — коробка окажется с обувью коричневого цвета, 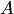 и и 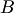 — несовместные события.Событие называется достоверным, если оно обязательно произойдет в условиях данного опыта.Событие называется невозможным, если оно не может произойти в условиях данного опыта. Например, событие, заключающееся в том, что из партии стандартных деталей будет взята стандартная деталь, является достоверным, а нестандартная — невозможным.Событие называется возможным, или случайным, если в результате опыта оно может появиться, но может и не появиться. Примером случайного события может служить выявление дефектов изделия при контроле партии готовой продукции, несоответствие размера обрабатываемого изделия заданному, отказ одного из звеньев автоматизированной системы управления.События называются равновозможными, если по условиям 1испытания ни одно из этих событий не является объективно более возможным, чем другие. Например, пусть магазину поставляют электролампочки (причем в равных количествах) несколько заводов-изготовителей. События, состоящие в покупке лампочки любого из этих заводов, равновозможны.Важным понятием является полная группа событий. Несколько соб в данном опыте образ полную группу, если в результате опыта обяз. появ. хотя быодноиз них. — несовместные события.Событие называется достоверным, если оно обязательно произойдет в условиях данного опыта.Событие называется невозможным, если оно не может произойти в условиях данного опыта. Например, событие, заключающееся в том, что из партии стандартных деталей будет взята стандартная деталь, является достоверным, а нестандартная — невозможным.Событие называется возможным, или случайным, если в результате опыта оно может появиться, но может и не появиться. Примером случайного события может служить выявление дефектов изделия при контроле партии готовой продукции, несоответствие размера обрабатываемого изделия заданному, отказ одного из звеньев автоматизированной системы управления.События называются равновозможными, если по условиям 1испытания ни одно из этих событий не является объективно более возможным, чем другие. Например, пусть магазину поставляют электролампочки (причем в равных количествах) несколько заводов-изготовителей. События, состоящие в покупке лампочки любого из этих заводов, равновозможны.Важным понятием является полная группа событий. Несколько соб в данном опыте образ полную группу, если в результате опыта обяз. появ. хотя быодноиз них.
3.Операции над событиями.
1.События А и В называются равными, если осуществление события А влечет за собой осуществление события В и наоборот. 2.Объединением или суммой событий Аk называется событие A, которое означает появление хотя бы одного из событий Аk. 3.Пересечением или произведением событий Ak называется событие А, которое заключается в осуществлении всех событий Ak. 4,Разностью событий А и В называется событие С, которое означает, что происходит событие А, но не происходит событие В. 5,Дополнительным к событию А называется событие , означающее, что событие А не происходит. Элементарными исходами опыта называются такие результаты опыта, которые взаимно исключают друг друга и в результате опыта происходит одно из этих событий, также каково бы ни было событие А, по наступившему элементарному исходу можно судить о том, происходит или не происходит это событие. Совокупность всех элементарных исходов опыта называется пространством элементарных событий.
4.Статистический подход к определению вероятности.
При рассмотрении результатов отдельных испытаний очень трудно найти какие-либо закономерности. Однако в последовательности одинаковых испытаний можно обнаружить устойчивость некоторых средних характеристик. Частостью какого-либо события в данной серии из n испытаний называется отношение m/n, числа m тех испытаний, в которых событие А наступило, к общему числу испытаний n. Почти в каждой достаточно длинной серии испытаний частость события А устанавливается около определенного значения , которое принимается за вероятность события А. Устойчивость значения частости подтверждается специальными экспериментами. Статистические закономерности такого рода были впервые обнаружены на примере азартных игр, т. е. на примере тех испытаний, которые характеризуются равновозможностью исходов. Это открыло путь для статистического подхода к численному определению вероятности, когда нарушается условие симметрии эксперимента. Частость события А называют статистической вероятностью, которая обозначается , (1.2)
где mA - число экспериментов, в которых появилось событие А;
n - общее число экспериментов.
Формулы (1.1) и (1.2) для определения вероятности имеют внешнее сходство, но они различны по существу. Формула (1.1) служит для теоретического вычисления вероятности события по заданным условиям опыта. Формула (1.2) служит для экспериментального определения частости события. Чтобы воспользоваться формулой (1.2), необходим опытный статистический материал.
6.Геометрический подход к определению вероятностей.
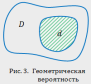
В классическом определении вероятности рассматривается полная группа конечного числа равновозможных событий. На практике очень часто число возможных исходов испытаний бесконечно. В таких случаях классическое определение вероятности неприменимо. Однако иногда в подобных случаях можно воспользоваться другим методом вычисления вероятности. Для определенности ограничимся двумерным случаем.Пусть на плоскости задана некоторая область 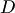 площадью площадью 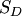 , в которой содержится другая область , в которой содержится другая область 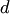 площадью площадью 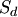 (рис. 3). В область (рис. 3). В область 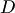 наудачу бросается точка. Чему равна вероятность того, что точка попадет в область наудачу бросается точка. Чему равна вероятность того, что точка попадет в область 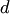 ? При этом предполагается, что наудачу брошенная точка может попасть в любую точку области ? При этом предполагается, что наудачу брошенная точка может попасть в любую точку области 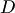 , и вероятность попасть в какую-либо часть области , и вероятность попасть в какую-либо часть области 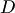 пропорциональна площади части и не зависит от ее расположения и формы. В таком случае вероятность попадания в область пропорциональна площади части и не зависит от ее расположения и формы. В таком случае вероятность попадания в область 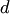 при бросании наудачу точки в область при бросании наудачу точки в область 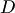
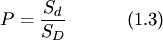 Таким образом, в общем случае, если возможность случайного появления точки внутри некоторой области на прямой, плоскости или в пространстве определяется не положением этой области и ее границами, а только ее размером, т. е. длиной, площадью или объемом, то вероятность попадания случайной точки внутрь некоторой области определяется как отношение размера этой области к размеру всей области, в которой может появляться данная точка. Это есть геометрическое определение вероятности. Таким образом, в общем случае, если возможность случайного появления точки внутри некоторой области на прямой, плоскости или в пространстве определяется не положением этой области и ее границами, а только ее размером, т. е. длиной, площадью или объемом, то вероятность попадания случайной точки внутрь некоторой области определяется как отношение размера этой области к размеру всей области, в которой может появляться данная точка. Это есть геометрическое определение вероятности.
5.Классический подход к определению вероятности. Свойства вероятности.
Для количественного сравнения событий по степени возможности их появления вводится числовая мера, которая называется вероятностью события.Вероятностью события называется число, являющееся выражением меры объективной возможности появления события.Вероятность события 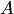 будем обозначать символом будем обозначать символом 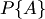 .Вероятность события .Вероятность события 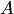 равна отношению числа случаев равна отношению числа случаев 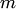 , благоприятствующих ему, из общего числа , благоприятствующих ему, из общего числа 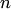 единственно возможных, равновозможных и несовместных случаев к числу единственно возможных, равновозможных и несовместных случаев к числу 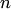 , т. е. , т. е.
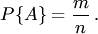 (1.1)Это есть классическое определение вероятности. Таким образом, для нахождения вероятности события необходимо, рассмотрев различные исходы испытания, найти совокупность единственно возможных, равновозможных и несовместных случаев, подсчитать общее их число (1.1)Это есть классическое определение вероятности. Таким образом, для нахождения вероятности события необходимо, рассмотрев различные исходы испытания, найти совокупность единственно возможных, равновозможных и несовместных случаев, подсчитать общее их число 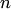 , число случаев , число случаев 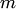 , благоприятствующих данному событию, и затем выполнить расчет по формуле (1.1).Из формулы (1.1) следует, что вероятность события является неотрицательным числом и может изменяться в пределах от нуля до единицы в зависимости от того, какую долю составляет благоприятствующее число случаев от общего числа случаев: , благоприятствующих данному событию, и затем выполнить расчет по формуле (1.1).Из формулы (1.1) следует, что вероятность события является неотрицательным числом и может изменяться в пределах от нуля до единицы в зависимости от того, какую долю составляет благоприятствующее число случаев от общего числа случаев:
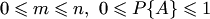
Отметим свойства вероятностиСвойство 1. Если все случаи являются благоприятствующими данному событию 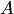 , то это событие обязательно произойдет. Следовательно, рассматриваемое событие является достоверным, а вероятность его появления , то это событие обязательно произойдет. Следовательно, рассматриваемое событие является достоверным, а вероятность его появления 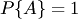 , так как в этом случае , так как в этом случае 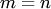 : :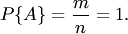 Свойство 2. Если нет ни одного случая, благоприятствующего данному событию Свойство 2. Если нет ни одного случая, благоприятствующего данному событию 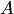 , то это событие в результате опыта произойти не может. Следовательно, рассматриваемое событие является невозможным, а вероятность его появления , то это событие в результате опыта произойти не может. Следовательно, рассматриваемое событие является невозможным, а вероятность его появления 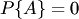 , так как в этом случае , так как в этом случае 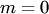 : :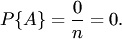 Свойство 3. Вероятность наступления событий, образующих полную группу, равна единице.Свойство 4. Вероятность наступления противоположного события Свойство 3. Вероятность наступления событий, образующих полную группу, равна единице.Свойство 4. Вероятность наступления противоположного события 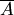 определяется так же, как и вероятность наступления, события определяется так же, как и вероятность наступления, события 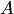 : :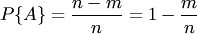 где где 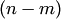 — число случаев, благоприятствующих появлению противоположного события — число случаев, благоприятствующих появлению противоположного события 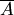 . Отсюда вероятность наступления противоположного события . Отсюда вероятность наступления противоположного события 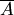 равна разнице между единицей и вероятностью наступления события равна разнице между единицей и вероятностью наступления события 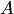 : :
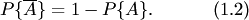 Важное достоинство классического определения вероятности события состоит в том, что с его помощью вероятность события можно определить, не прибегая к опыту, а исходя из логических рассуждений.Пример 1. Набирая номер телефона, абонент забыл одну цифру и набрал ее наудачу. Найти вероятность того, что набрана нужная цифра.Решение. Обозначим Важное достоинство классического определения вероятности события состоит в том, что с его помощью вероятность события можно определить, не прибегая к опыту, а исходя из логических рассуждений.Пример 1. Набирая номер телефона, абонент забыл одну цифру и набрал ее наудачу. Найти вероятность того, что набрана нужная цифра.Решение. Обозначим 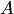 событие, состоящее в том, что набрана нужная цифра. Абонент мог набрать любую из 10 цифр, поэтому общее число возможных исходов равно 10. Эти исходы единственно возможны (одна из цифр набрана обязательно) и равновозможны (цифра набрана наудачу). Благоприятствует событию событие, состоящее в том, что набрана нужная цифра. Абонент мог набрать любую из 10 цифр, поэтому общее число возможных исходов равно 10. Эти исходы единственно возможны (одна из цифр набрана обязательно) и равновозможны (цифра набрана наудачу). Благоприятствует событию 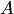 лишь один исход (нужная цифра лишь одна). Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех исходов: лишь один исход (нужная цифра лишь одна). Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех исходов:
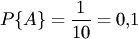 . .
7.Элементы комбинаторики.
В теории вероятностей часто используют размещения, перестановки и сочетания. Если дано множество 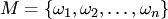 , то размещением (сочетанием) из , то размещением (сочетанием) из 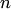 элементов по элементов по 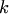 называется любое упорядоченное (неупорядоченное) подмножество называется любое упорядоченное (неупорядоченное) подмножество 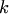 элементов множества элементов множества 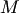 . При . При 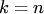 размещение называется перестановкой из размещение называется перестановкой из 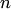 элементов.Пусть, например, дано множество элементов.Пусть, например, дано множество 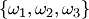 . Размещениями из трех элементов этого множества по два являются . Размещениями из трех элементов этого множества по два являются 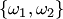 , , 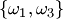 , , 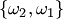 , , 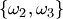 , , 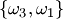 , , 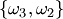 ; сочетаниями — ; сочетаниями — 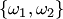 , , 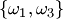 , , 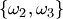 .Два сочетания различаются хотя бы одним элементом, а размещения различаются либо самими элементами, либо порядком их следования. Число сочетаний из .Два сочетания различаются хотя бы одним элементом, а размещения различаются либо самими элементами, либо порядком их следования. Число сочетаний из 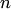 элементов по элементов по 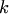 вычисляется по формуле вычисляется по формуле
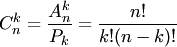 где где
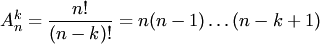
есть число размещений из 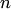 элементов по элементов по 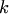 ; ; 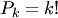 — число перестановок из — число перестановок из 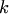 элементов.Пример 2. В партии из 10 деталей имеется 7 стандартных. Найти вероятность того, что среди взятых наудачу 6 деталей ровно 4 стандартных.Решение. Общее число возможных исходов испытания равно числу способов, которыми можно извлечь 6 деталей из 10, т. е. равно элементов.Пример 2. В партии из 10 деталей имеется 7 стандартных. Найти вероятность того, что среди взятых наудачу 6 деталей ровно 4 стандартных.Решение. Общее число возможных исходов испытания равно числу способов, которыми можно извлечь 6 деталей из 10, т. е. равно 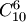 — числу сочетаний из 10 элементов по 6. Число исходов, благоприятствующих событию — числу сочетаний из 10 элементов по 6. Число исходов, благоприятствующих событию 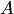 (среди 6 взятых деталей ровно 4 стандартных), определяем так: 4 стандартные детали можно взять из 7 стандартных деталей (среди 6 взятых деталей ровно 4 стандартных), определяем так: 4 стандартные детали можно взять из 7 стандартных деталей 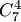 способами; при этом остальные способами; при этом остальные 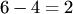 детали должны быть нестандартными; взять же 2 нестандартные детали из детали должны быть нестандартными; взять же 2 нестандартные детали из 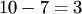 нестандартных деталей можно нестандартных деталей можно 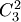 способами. Следовательно, число благоприятствующих исходов равно способами. Следовательно, число благоприятствующих исходов равно 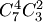 . Исходная вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех исходов: . Исходная вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех исходов:
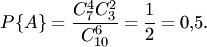
8. Условная вероятность. Независимые события.
Различают события зависимые и независимые. Два события называются независимыми, если появление одного из них не изменяет вероятность появления другого. Например, если в цехе работают две автоматические линии, по условиям производства не взаимосвязанные, то остановки этих линий являются независимыми событиями.
Пример 3. Монета брошена два раза. Вероятность появления "герба" в первом испытании (событие ) не зависит от появления или не появления "герба" во втором испытании (событие ). В свою очередь, вероятность появления "герба" во втором испытании не зависит от результата первого испытания. Таким образом, события и независимые.
Несколько событий называются независимыми в совокупности, если любое из них не зависит от любого другого события и от любой комбинации остальных.
События называются зависимыми, если одно из них влияет на вероятность появления другого. Например, две производственные установки связаны единым технологическим циклом. Тогда вероятность выхода из строя одной из них зависит от того, в каком состоянии находится другая. Вероятность одного события , вычисленная в предположении осуществления другого события , называется условной вероятностью события и обозначается .
Условие независимости события от события записывают в виде , а условие его зависимости — в виде . Рассмотрим пример вычисления условной вероятности события.
Пример 4. В ящике находятся 5 резцов: два изношенных и три новых. Производится два последовательных извлечения резцов. Определить условную вероятность появления изношенного резца при втором извлечении при условии, что извлеченный в первый раз резец в ящик не возвращается.
Решение. Обозначим извлечение изношенного резца в первом случае, а — извлечение нового. Тогда . Поскольку извлеченный резец в ящик не возвращается, то изменяется соотношение между количествами изношенных и новых резцов. Следовательно, вероятность извлечения изношенного резца во втором случае зависит от того, какое событие осуществилось перед этим.
Обозначим событие, означающее извлечение изношенного резца во втором случае. Вероятности этого события могут быть такими:
9 Вероятность суммы событий и произведения событий.
Суммой двух событий и называется событие , состоящее в выполнении события или события , или обоих вместе.
Например, если событие – попадание в цель при первом выстреле, событие – попадание в цель при втором выстреле, то событие есть попадание в цель вообще, безразлично при каком выстреле – при первом, при втором или при обоих вместе.
Если события и несовместимы, то естественно, что появление этих событий вместе отпадает, и сумма событий и сводится к появлению или события , или события . Например, если событие – появление карты червонной масти при вынимании карты из колоды, событие – появление карты бубновой масти, то есть появление карты красной масти, безразлично – червонной или бубновой.
Короче, суммой двух событий и называется событие , состоящее в появлении хотя бы одного из событий и .
Суммой нескольких событий называется событие, состоящее в появлении хотя бы одного из этих событий.
Например, если опыт состоит в пяти выстрелах по мишени и даны события:
– ни одного попадания,
– ровно одно попадание,
– ровно два попадания,
- ровно три попадания,
– ровно четыре попадания,
– ровно пять попаданий,
То есть событие «не более двух попаданий», а
есть событие «не менее трех попаданий».
Произведением двух событий и называется событие , состоящее в совместном выполнении события и события .
Например, если событие – появление туза при вынимании карты из колоды, событие – появление карты бубновой масти, то событие есть появление бубнового туза. Если производится два выстрела по мишени и событие – попадание при первом выстреле, событие – попадание при втором выстреле, то есть попадание при обоих выстрелах.
Произведением нескольких событий называется событие, состоящее в совместном появлении всех этих событий.
Например, если по мишени производится три выстрела, и рассматриваются события
– промах при первом выстреле,
– промах при втором выстреле,
- промах при третьем выстреле,
то событие
состоит в том, что в мишень не будет ни одного попадания.
При определении вероятностей часто приходится представлять сложные события в виде комбинаций более простых событий, применяя и операцию сложения, и операцию умножения событий.
Например, пусть по мишени производится три выстрела, и рассматриваются следующие элементарные события:
- попадание при первом выстреле,
- промах при первом выстреле,
- попадание при втором выстреле,
- промах при втором выстреле,
- попадание при третьем выстреле,
- промах при третьем выстреле.
10 Формула полной вероятности. Формула Байеса.
Теорема Байеса, Формула Байеса — одна из основных теорем элементарной теории вероятностей, которая позволяет определить вероятность того, что произошло какое-либо событие (гипотеза) при наличии лишь косвенных тому подтверждений (данных), которые могут быть неточны. Названа в честь ее автора, преп. Томаса Байеса (посвященная ей работа «An Essay towards solving a Problem in the Doctrine of Chances» впервые опубликована в 1763 году,[1] через 2 года после смерти автора). Полученную по формуле вероятность можно далее уточнять, принимая во внимание данные новых наблюдений.
Психологические эксперименты[2] показали, что люди при оценках вероятности игнорируют различие априорных вероятностей (ошибка базовой оценки), и потому правильные результаты, получаемые по теореме Байеса, могут очень отличаться от ожидаемых.
Формула Байеса:
,

где
P(A) — априорная вероятность гипотезы A (смысл такой терминологии см. ниже);
P(A | B) — вероятность гипотезы A при наступлении события B (апостериорная вероятность);
P(B | A) — вероятность наступления события B при истинности гипотезы A;
P(B) — вероятность наступления события B.
11 Понятие случайной величины. Типы случайны величин. Закон распределения.
Случайная величина — это величина, которая принимает в результате опыта одно из множества значений, причём появление того или иного значения этой величины до её измерения нельзя точно предсказать.
В практических приложениях наиболее часто используются два типа случайных величин: дискретные и абсолютно непрерывные, хотя, разумеется, существуют случайные величины, не относящиеся ни к одному из этих классов.
Дискретные случайные величины
Дискретная случайная величина - это величина, принимающая конечное или счетное число значений. Такая величина задается набором этих значений и их вероятностей , , которые должны быть неотрицательными и удовлетворять условию нормировки: .
При этом вероятностная мера на любом (борелевском) множестве прямой задается по формуле:
, где .
Абсолютно непрерывные случайные величины
Если функция распределения случайной величины имеет вид:
, где - интегрируемая неотрицательная функция,
тогда эта случайная величина называется абсолютно непрерывной. Функция при этом называется плотностью распределения. Плотность распределения удовлетворяет свойствам:
и .
И наоборот, любая интегрируемая функция , удовлетворяющая этим свойствам, может быть взята в качестве плотности распределения некоторой случайной величины.
Поскольку функция распределения является функцией верхнего предела от плотности, то последняя восстанавливается по ней дифференцированием:
. Определение. Нормальным называется распределение вероятностей непрерывной случайной величины, которое описывается плотностью вероятности
Нормальный закон распределения также называется законом Гаусса.
Нормальный закон распределения занимает центральное место в теории вероятностей. Это обусловлено тем, что этот закон проявляется во всех случаях, когда случайная величина является результатом действия большого числа различных факторов. К нормальному закону приближаются все остальные законы распределения.
Можно легко показать, что параметры и , входящие в плотность распределения являются соответственно математическим ожиданием и средним квадратическим отклонением случайной величины Х.
Найдем функцию распределения F(x).
График плотности нормального распределения называется нормальной кривой или кривой Гаусса.
Нормальная кривая обладает следующими свойствами:
1) Функция определена на всей числовой оси.
2) При всех х функция распределения принимает только положительные значения.
3) Ось ОХ является горизонтальной асимптотой графика плотности вероятности, т.к. при неограниченном возрастании по абсолютной величине аргумента х, значение функции стремится к нулю.
4) Найдем экстремум функции.
Т.к. при y’ > 0 при x < m и y’ < 0 при x > m , то в точке х = т функция имеет максимум, равный .
5) Функция является симметричной относительно прямой х = а, т.к. разность
(х – а) входит в функцию плотности распределения в квадрате.
6) Для нахождения точек перегиба графика найдем вторую производную функции плотности.
При x = m + s и x = m - s вторая производная равна нулю, а при переходе через эти точки меняет знак, т.е. в этих точках функция имеет перегиб.
В этих точках значение функции равно .
Построим график функции плотности распределения.
Построены графики при т =0 и трех возможных значениях среднего квадратичного отклонения s = 1, s = 2 и s = 7. Как видно, при увеличении значения среднего квадратичного отклонения график становится более пологим, а максимальное значение уменьшается..
Если а > 0, то график сместится в положительном направлении, если а < 0 – в отрицательном.
При а = 0 и s = 1 кривая называется нормированной. Уравнение нормированной кривой.
12 Дискретные случайные величины.
Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед не известное и зависящее от случайных причин, которые заранее не могут быть учтены.
Дискретной называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями.
Число возможных значений дискретной случайной величины может быть конечным или бесконечным.
Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями.
Закон распределения дискретной случайной величины можно задать таблично, в виде формулы (аналитически) и графически.
13 Непрерывные случайные величины.
Случайная величина, значения которой заполняют некоторый промежуток, называется непрерывной.
В частных случаях это может быть не один промежуток, а объединение нескольких промежутков. Промежутки могут быть конечными, полу¬бесконечными или бесконечными, например: (a; b], (–µ ; a), [b;µ), (–µ; µ).
Вообще непрерывная случайная величина – это абстракция. Снаряд, выпущенный из пушки, может пролететь любое расстояние, скажем, от 5 до 5,3 километров, но никому не придёт в голову измерять эту величину с точностью до 0,0000001 километра (то есть до миллиметра), не говоря уже об абсолютной точности. В практике такое расстояние будет дискретной случайной величиной, у которой одно значение от другого отличается по крайней мере на 1 метр.
При описании непрерывной случайной величины принципиально невозможно выписать и занумеровать все её значения, принадлежащие даже достаточно узкому интервалу. Эти значения образуют несчётное множество, называемое «континуум».
15. Равномерное распределение,
прямоугольное распределение, специальный вид распределения вероятностей случайной величины Х, принимающей значения из интервала (а — h, a + h); характеризуется плотностью вероятности: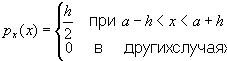 .Математическое ожидание: Ех = a, дисперсия Dx = h2/3, характеристическая .Математическое ожидание: Ех = a, дисперсия Dx = h2/3, характеристическая
функция: 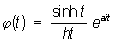 .С помощью линейного преобразования интервал (а — h, a + h) может быть переведён в любой заданный интервал. Так, величина Y = (X — a + h)/2h равномерно распределена на интервале (0, 1). Если Y1, Y2,..., Yn равномерно распределены на интервале (0, 1), то закон распределения их суммы, нормированной математическим ожиданием n/2 и дисперсией n/12, при возрастании n быстро приближается к нормальному распределению (даже при n = 3 приближение часто бывает достаточным для практики). .С помощью линейного преобразования интервал (а — h, a + h) может быть переведён в любой заданный интервал. Так, величина Y = (X — a + h)/2h равномерно распределена на интервале (0, 1). Если Y1, Y2,..., Yn равномерно распределены на интервале (0, 1), то закон распределения их суммы, нормированной математическим ожиданием n/2 и дисперсией n/12, при возрастании n быстро приближается к нормальному распределению (даже при n = 3 приближение часто бывает достаточным для практики).
17. Пуассона распределение,
одно из важнейших распределений вероятностей случайных величин, принимающих целочисленные значения. Подчинённая П. р. случайная величина Х принимает лишь неотрицательные значения, причём Х = kc вероятностью , k =0, 1, 2,...
(l — положительный параметр). Если независимые случайные величины X1 и X2 имеют П. р. с параметрами l1 и l2, то их сумма X1 + X2 имеет П. р. с параметрами l1 + l2. В теоретико-вероятностных моделях П. р. используется как аппроксимирующее и как точное распределение. Например, если при n независимых испытаниях события A1,..., An осуществляются с одной и той же малой вероятностью р, то вероятность одновременного осуществления каких-либо k событий (из общего числа n) приближённо выражается функцией pk(np) (математическое содержание этого утверждения при больших значениях n и1/р формулируются Пуассона теоремой). В частности, такая модель хорошо описывает процесс радиоактивного распада и многие др. физические явления. Как точное П. р. появляется в теории случайных процессов. Например, при расчёте нагрузки линий связи обычно предполагают, что количества вызовов, поступивших за непересекающиеся интервалы времени, суть независимые случайные величины, подчиняющиеся П. р. с параметрами, значения которых пропорциональны длинам соответствующих интервалов времени В качестве оценки неизвестного параметра l по n наблюдённым значениям независимых случайных величин X1,..., Xn используется их арифметическое среднее X =(X1 +... + Xn)/n, поскольку эта оценка лишена систсматической ошибки и её квадратичное отклонение минимально.
14 Параметры распределения случайных величин.
Распределение числовой случайной величины – это функция, которая однозначно определяет вероятность того, что случайная величина принимает заданное значение или принадлежит к некоторому заданному интервалу.
Первое – если случайная величина принимает конечное число значений. Тогда распределение задается функцией Р(Х = х), ставящей каждому возможному значению х случайной величины Х вероятность того, что Х = х.
Второе – если случайная величина принимает бесконечно много значений. Это возможно лишь тогда, когда вероятностное пространство, на котором определена случайная величина, состоит из бесконечного числа элементарных событий. Тогда распределение задается набором вероятностей P(a
P(a
Это соотношение показывает, что как распределение может быть рассчитано по функции распределения, так и, наоборот, функция распределения – по распределению
При статистическом моделировании и первичной обработке данных используются следующие инструменты: Генерация случайных чисел, Гистограмма.
Инструмент Генерация случайных чисел заполняет интервал независимыми случайными числами.
При помощи параметра Число переменных вы можете получить многомерную выборку. Для этого введите число столбцов в выходной таблице.
Параметром Число случайных чисел определяется число точек данных, которое вы хотите генерировать для каждой переменной.
Выбор закона распределения случайных чисел задаётся параметром Распределение.
Равномерное распределение характеризуется верхней и нижней границами. Вероятность попадания переменной в отрезок фиксированной длины зависит только от длины отрезка и не зависит от его расположения на интервале. Как правило, в приложениях используют равномерное распределение в интервале [0,1].
Нормальное распределение характеризуется средним значением и стандартным отклонением. Обычно приложения для этого распределения используют среднее значение 0 и стандартное отклонение 1.
Распределение Бернулли характеризуется вероятностью успеха в данном испытании. Случайная величина принимает значение 0 или 1. Например, при бросании игральной кости или выпадет 6 очков с вероятностью 1/6 или выпадет не 6 очков с вероятностью 5/6, то есть случайная величина принимает значение 1 с вероятностью 1/6 или 0 с вероятностью 5/6.
Биноминальное распределение характеризуется вероятностью успеха для некоторого числа испытаний. Например, вы можете генерировать случайные числа, моделирующие процесс бросания монеты с вероятностью успеха ровно в “k” случаях из “n” испытаний.
Распределение Пуассона характеризуется значением Лямбда, равным 1/среднее. Распределение Пуассона часто используется для характеристики числа событий, случающихся в единицу времени, например, число телефонных соединений в минуту.
Модельное распределение характеризуется нижней и верхней границей, шагом, числом повторений значений и числом повторений последовательности.
Дискретное распределение характеризуется значением и связанным с ним интервалом вероятности. Интервал должен содержать два столбца: левый содержит значения, правый – вероятности, связанные со значением в данной строке. Сумма вероятностей должна быть равна 1.
16. Биномальное распределение
Пусть 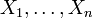 — конечная последовательность независимых случайных величин с распределением Бернулли, то есть — конечная последовательность независимых случайных величин с распределением Бернулли, то есть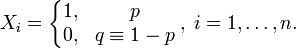 Построим случайную величину Построим случайную величину 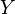 : :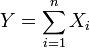 . .
Тогда 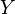 , число единиц (успехов) в последовательности , число единиц (успехов) в последовательности 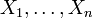 , имеет биномиальное распределение с , имеет биномиальное распределение с 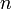 степенями свободы и вероятностью «успеха» степенями свободы и вероятностью «успеха» 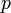 . Пишем: Y∼Bin(n,p). Её функция плотности вероятности задаётся формулой: . Пишем: Y∼Bin(n,p). Её функция плотности вероятности задаётся формулой:
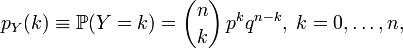 где где 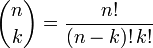 — биномиальный коэффициент. — биномиальный коэффициент.
Функция распределения
Функция распределения биномиального распределения может быть записана в виде суммы:
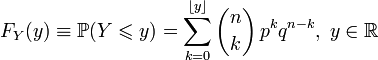 , ,
где 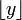 обозначает наибольшее целое, не превосходящее число y, или в виде неполной бета-функции: обозначает наибольшее целое, не превосходящее число y, или в виде неполной бета-функции:
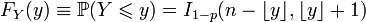 . .
|
 Скачать 224.21 Kb.
Скачать 224.21 Kb.