Контрольня работа. контрольная работа. 1. Теоретическая часть
 Скачать 1.02 Mb. Скачать 1.02 Mb.
|
|
Содержание 1. Теоретическая часть ………………………………………………………….. 3 1.1 Природа потоков в сетях и принцип их сохранения …………………… 3 2. Практическая часть …………………………………………………………... 8 2.1 Общая постановка задач линейного программирования ………………. 8 2.2 Элементы теории игр …………………………………………………...... 9 2.3 Планирование производства с помощью сетевых моделей ………….... 9 Список литературы …………………….………………………………………. 16 Теоретическая часть 1.1 Природа потоков в сетях и принцип их сохранения Одной из наиболее важных задач теории графов является задача определения максимального потока, протекающего от некоторой вершины графа s (источника) к вершине t (стоку). Примерами таких задач могут быть: перевозка наибольшего товара, максимальное количество жидкости и газа, транспортируемых по трубопроводам, информация по компьютерной и телефонной сети и др. Сетью называется ориентированный конечный связный граф без циклов и петель, имеющий начальную вершину (источник) и конечную вершину (сток). Примерами вершин сети могут быть пересечения автострад, электростанции, телефонные узлы, железнодорожные узлы, аэропорты, водохранилища, товарные склады. Примерами дуг сети могут быть дороги, линии электропередачи, телефонные линии, авиалинии, водные магистрали, нефте- и газопроводы и т.д. 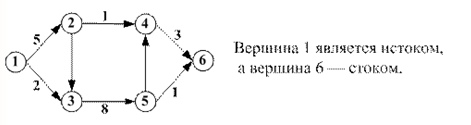 Рис. 1 – Пример транспортной сети. Сходство сетевых представлений наблюдается в природе, технике и различных сферах деятельности человека. Так, например, с высоты птичьего полёта или самолёта можно наблюдать сетевую модель формирования реки, например, Волги, от её истоков маленькие ручейки и реки, соединяясь во взаимосвязанные артерии, объединяются в одно большое русло, по которому потоки воды устремляются в Каспийское море. Такие же аналогии представляют собой сети железных дорог, по которым транспортные потоки направляются из пунктов отправления в пункты назначения, осуществляя перевозку потоков грузов и пассажиров. Совокупность линий электропередач также представляют собой энергетическую сеть, по которой потоки электроэнергии от электростанций по проводам поступают к потребителям. Автомобильные дороги как в масштабе города, района, области, так и в более крупных масштабах страны или, например, континента, представляют собой сети, по которым движутся потоки автомобилей. Нефте- и газопроводы в совокупности представляют собой сети трубопроводов, по которым потоки нефти или газа поступают от источников к потребителям. Водопроводные сети обеспечивают движение потоков воды по трубопроводам от источников к потребителям. Аналогичные сети представляют собой маршруты движения кораблей и самолётов, обеспечивающие перемещение потоков пассажиров и грузов по планете. Такие же аналогии представляют собой телефонные, радио- и телекоммуникационные сети, по которым циркулируют информационные потоки, например, компьютерные сети связи различного назначения. Особый интерес представляют сети, образованные движением товарных и финансовых потоков, изучение которых может пояснить очень многие явления нашей жизни. Перечисленные сетевые аналогии потоковых процессов имеют динамический характер, связанный с перемещениями различных по своей природе масс в пространстве: электроэнергии, нефти, газа, воды, воздуха, железнодорожного, воздушного, автомобильного транспорта, товаров, финансов, пешеходов, информации и т.п. Причём существование этих потоков необходимо для обеспечения и поддержания жизнедеятельности человека. Сетевое представление взаимодействия и циркуляции потоков необходимо, чтобы оценить и вычислить разные характеристики, описывающие условия существования и поведения потоков в таких средах. Множество возникающих в таких случаях задач может быть решено с помощью теории потоков в сетях. В этой теории в качестве основы рассматриваются движения в сетях потоков любой природы от источника s к стоку t. Потоком f в сети G является действительная функция f: V x V → R, удовлетворяющая условиям: 1) 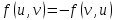 (антисимметричность); (антисимметричность);2) 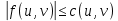 (ограничение пропускной способности), если ребра нет, то (ограничение пропускной способности), если ребра нет, то 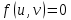 ; ;3) 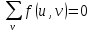 для всех вершин u, кроме s и t (закон сохранения потока). для всех вершин u, кроме s и t (закон сохранения потока). Величина потока f определяется как: 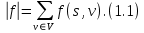 Также существует альтернативное определение (по Асанову), не вводящее антисимметричность. Поток f в сети G = (V, E, c) называется функция f: E→R, удовлетворяющая условиям: 1) Величина потока по каждой дуге не должна превосходить её пропускной способности: 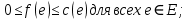 2) Величина потока, входящего в каждую вершину сети, за исключением входа и выхода, равна величине потока, выходящего из этой вершины: 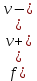 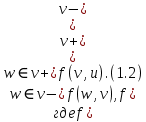 Здесь s – источник, а t – сток сети G (s имеет нулевую степень захода, а t имеет нулевую степень исхода); через v+ обозначено множество вершин, к которым идут дуги из вершины v; через v– обозначено множество вершин, из которых идут дуги в вершину v; c(e) называется пропускной способностью дуги е и неотрицательно. Число f(v,w) можно интерпретировать, например, как количество жидкости, поступающей из v в w по дуге (v,w). С этой точки зрения значение f(v−) может быть интерпретировано как поток, втекающий в вершину v, а f(v+) — вытекающий из v. Условие 1) называется условием ограничения по пропускной способности, а условие 2) — условием сохранения потока в вершинах; иными словами, поток, втекающий в вершину v, отличную от s или t, равен вытекающему из неё потоку. Пример сети с источником s и стоком t. 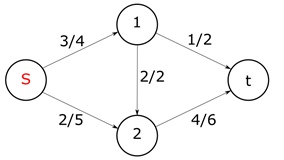 Рис. 2 – Сеть с источником s и стоком t Первое число означает величину потока, второе — пропускную способность ребра. Отрицательные величины потока не указаны (так как они мгновенно получаются из антисимметричности: 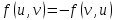 ). Сумма входящих рёбер везде (кроме источника и стока) равна сумме исходящих и на то, что в общем ). Сумма входящих рёбер везде (кроме источника и стока) равна сумме исходящих и на то, что в общем 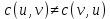 . Кроме того, величина потока на ребре никогда не превышает пропускную способность этого ребра. . Кроме того, величина потока на ребре никогда не превышает пропускную способность этого ребра.Величина потока в этом примере равна 3+2=5 (считаем от вершины s). Величина потока есть сумма потоков, выходящих из истока, или сумма потоков, входящих в сток сети. Для любой транспортной сети величина потока имеет максимальное значение, которое определяется теоремой Форда – Фалкерсона, которая утверждает, что величина максимального потока в сети равна величине минимального разреза, где разрезом транспортной сети называется такое множество дуг, удаление которых отделяет исток от стока. Минимальным разрезом транспортной сети называется разрез с минимальной пропускной способностью. Из определения потока следует, что величина потока не исчезает и не накапливается в вершинах сети, и, следовательно, количество потока, выходящего из входа s, равно количеству потока, заходящему в выход t. Это значение называется величиной потока V. Таким образом, поток в сети сохраняется, а величина потока равняется сумме значений потоков, выходящих из вершины s или входящих в вершину t. 2. Практическая часть 2.1 Общая постановка задач линейного программирования № 6. В задаче составить экономико-математическую модель. На двух автоматических линиях выпускают аппараты трёх типов. Другие условия задачи приведены в таблице.
Составить такой план загрузки станков, чтобы затраты были минимальными, а задание выполнено не более чем за 10 суток. Решение: Составим экономико-математическую модель задачи. Через х1А, х1В, х1С обозначим время, в течение которого первая линия будет занята выпуском аппаратов А, В и С. Аналогично обозначим через х2А, х2В, х2С – время, в течение которого вторая линия будет занята выпуском аппаратов А, В и С. 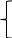 Так как время работы каждой линии ограничено десятью сутками, то: Так как время работы каждой линии ограничено десятью сутками, то: 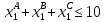 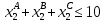  По плану: По плану: 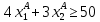 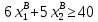 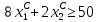 Также: 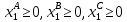 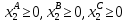 . .Целевая функция: 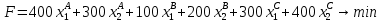 2.2 Элементы теории игр № 9.  Для следующей платёжной матрицы определить нижнюю и верхнюю цены игры, минимаксные стратегии и оптимальные решения игры, если существует седловая точка. Для следующей платёжной матрицы определить нижнюю и верхнюю цены игры, минимаксные стратегии и оптимальные решения игры, если существует седловая точка.
  Bi Решение:
Анализируя строки матрицы (стратеги игрока А) заполняем столбец ai: а1=0,3; а2=0,2; а3=0,4 – минимальные числа в строках 1, 2 и 3. Аналогично b1=0,9; b2=0,6; b3=0,8 – максимальные числа в столбцах 1, 2 и 3 соответственно. Нижняя цена игры a = max ai = max (0,3; 0,2; 0,4) = 0,4 (наибольшее число в столбце ai) и верхняя цена игры b = min bj = min (0,9; 0,6; 0,8) = 0,6 (наименьшее число в строке bj). Эти значение не равны, то есть a ≠ b, следовательно, седловая точка отсутствует. 2.3 Планирование производства с помощью сетевых моделей № 1. Построить сетевой график, определить длину критического пути и резервы времени при полной определённости во времени выполнения работ.
Решение: Полагаем, что i0 =0, i1=4, узлам 2, 3 и 4 непосредственно предшествует только узел 1: i2 = d12 = 13, i3 = d13 = 8, i4 = d14 = 9. Далее находим: i5 = max (i2 + d25; i3 + d35; i4 + d45) = (21; 9; 19) = 21 i6 = max (i2 + d26; i5 + d56) = (35; 28) = 35 i7 = max (i4 + d47) = 15 i8 = max (i7 + d78) = 21 i9 = max (i6 + d69) =44 i10 = max (i6 + d610) = 44 i11 = max (i9 + d911; i10 + d1011) = (48; 56) = 56 i12 = max (i8 + d812; i5 + d512; i11 + d1112) = (36; 26; 57) = 57 i13 = max (i12 + d1213) = 70 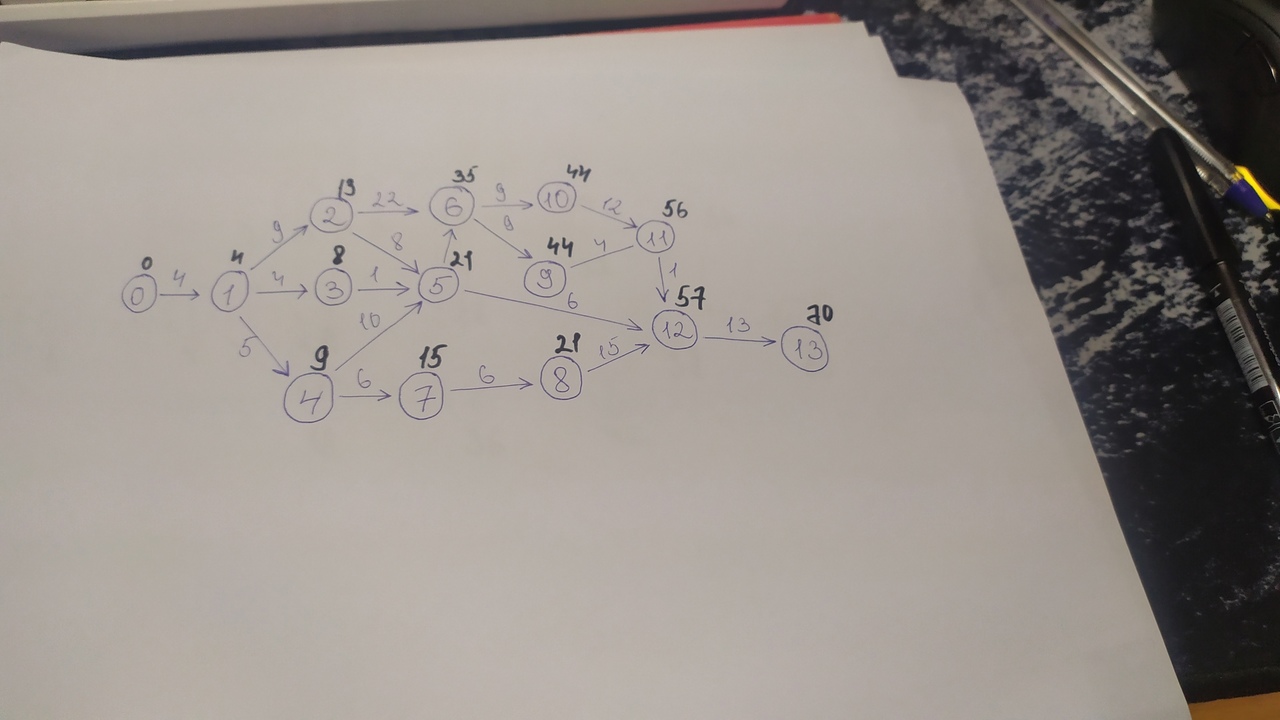 Поздний срок: u13 = 70 u12 = min (u13 – d1312) = 57 u11 = min (u12 – d1211) = 56 u10 = min (u11 – d1110) = 44 u9 = min (u11 – d119) = 52 u8 = min (u12 – d128) = 42 u7 = min (u8 – d87) = 36 u6 = min (u9 – d96; u10 – d106) = (43; 35) = 35 u5 = min (u6 – d65; u12 – d125) = (28; 51) = 28 u4 = min (u5 – d54; u7 – d74) = (18; 30) = 18 u3 = min (u5 – d53) = 27 u2 = min (u5 – d52; u6 – d62) = (20; 13) = 13 u1 = min (u2 – d21; u3 – d31; u4 – d41) = (4; 23; 13) = 4 u0 = min (u1 – d10) = 0 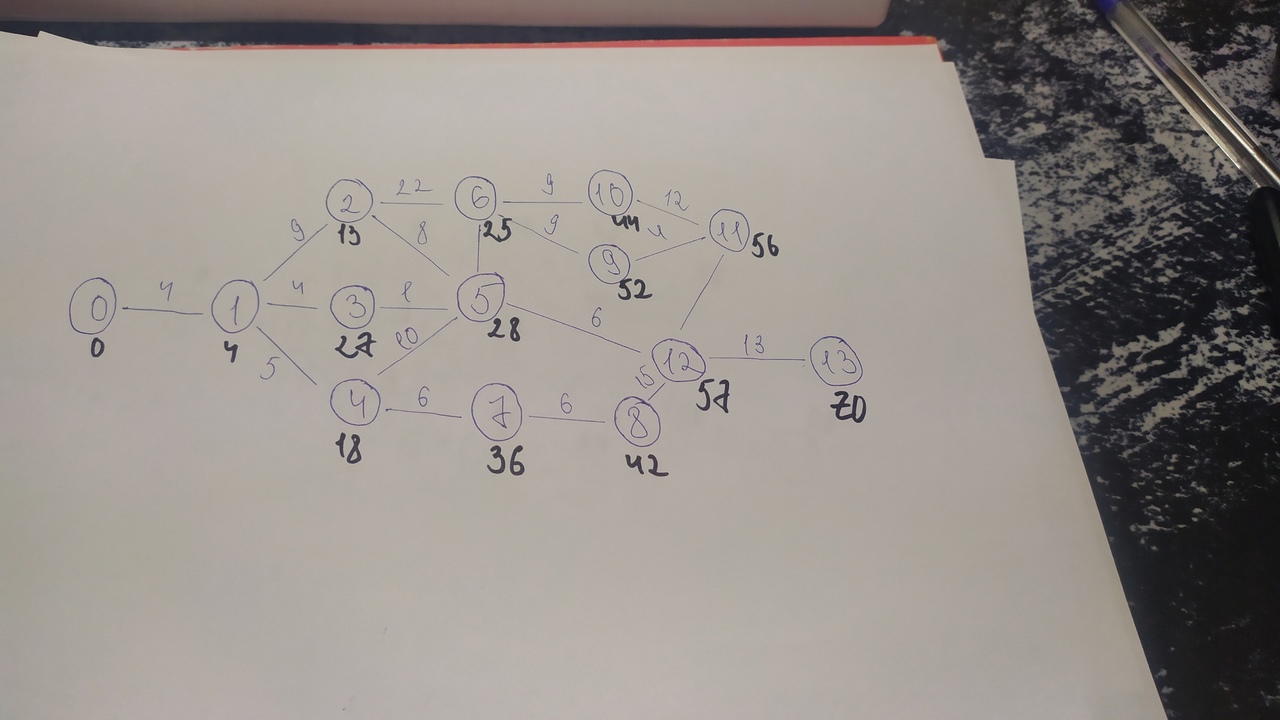
Критический путь: 0 – 1 – 2 – 6 – 10 – 11 – 12 – 13 = 70 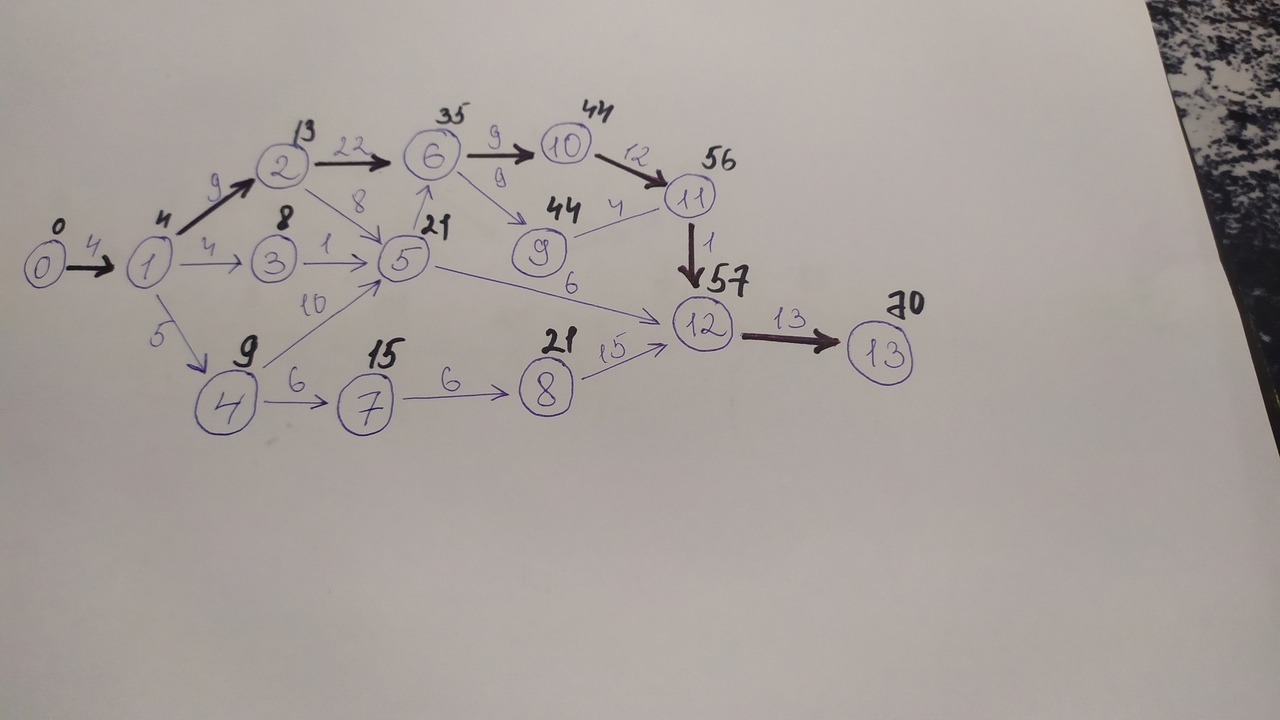 № 11. Построить сетевой график, определить длину критического пути и резервы времени при полной определённости во времени выполнения работ.
Решение: Полагаем, что i0 =0, i1=5, узлам 2, 3 и 4 непосредственно предшествует только узел 1: i2 = d12 = 12, i3 = d13 = 9, i4 = d14 = 9. Далее находим: i5 = max (i2 + d25; i3 + d35; i4 + d45) = (22; 16; 18) = 22 i6 = max (i2 + d26; i5 + d56) = (36; 32) = 36 i7 = max (i4 + d47) = 21 i8 = max (i7 + d78) = 24 i9 = max (i6 + d69) =40 i10 = max (i6 + d610) = 47 i11 = max (i9 + d911; i10 + d1011) = (58; 54) = 58 i12 = max (i8 + d812; i5 + d512; i11 + d1112) = (38; 27; 68) = 68 i13 = max (i12 + d1213) = 80 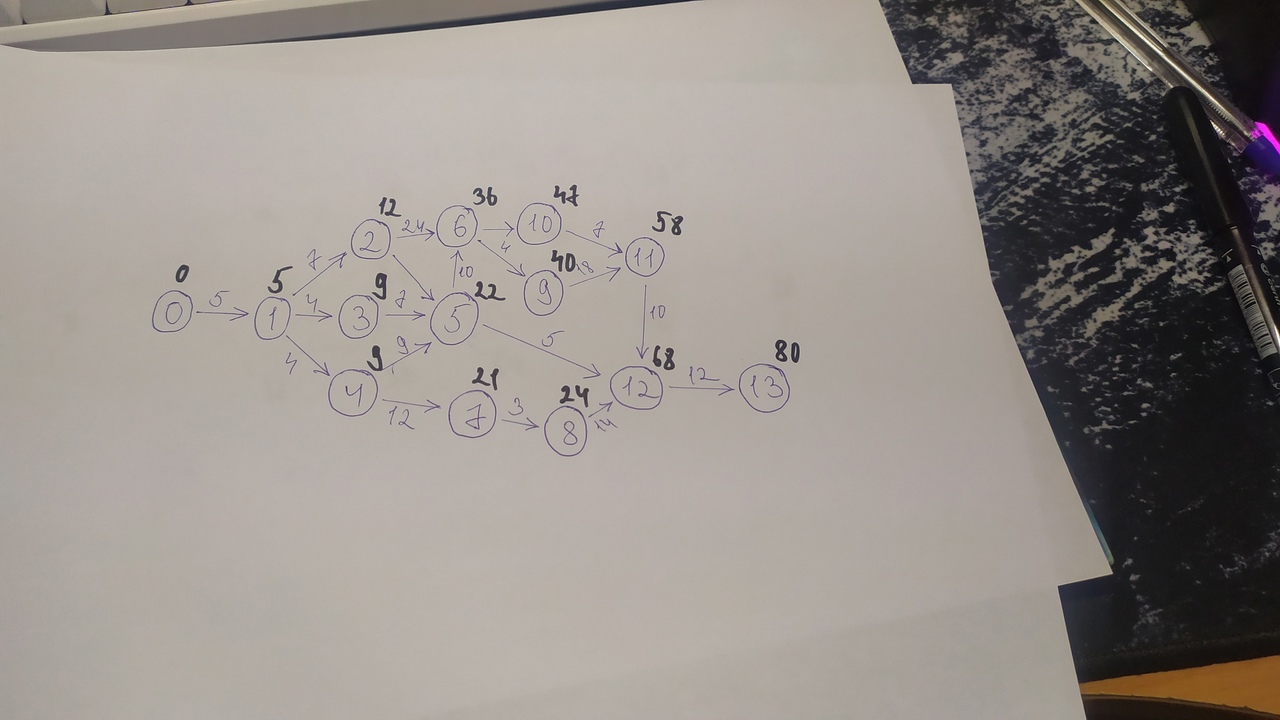 Поздний срок: u13 = 80 u12 = min (u13 – d1312) = 68 u11 = min (u12 – d1211) = 58 u10 = min (u11 – d1110) = 51 u9 = min (u11 – d119) = 40 u8 = min (u12 – d128) = 54 u7 = min (u8 – d87) = 33 u6 = min (u9 – d96; u10 – d106) = (36; 40) = 36 u5 = min (u6 – d65; u12 – d125) = (26; 63) = 26 u4 = min (u5 – d54; u7 – d74) = (17; 21) = 17 u3 = min (u5 – d53) = 19 u2 = min (u5 – d52; u6 – d62) = (16; 12) = 12 u1 = min (u2 – d21; u3 – d31; u4 – d41) = (5; 15; 13) = 5 u0 = min (u1 – d10) = 0 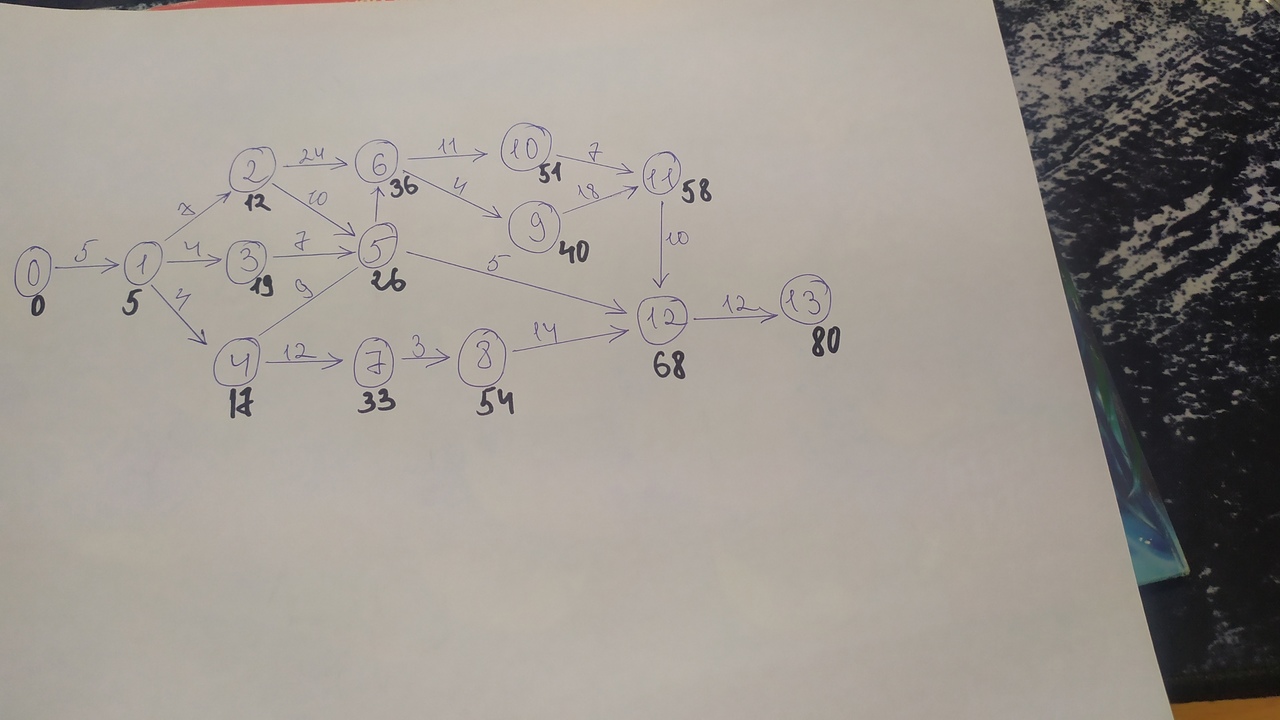
Критический путь: 0 – 1 – 2 – 6 – 9 – 11 – 12 – 13 = 80 Список литературы Алпатов, Ю.Н. Математическое моделирование производственных процессов: Учебное пособие / Ю.Н. Алпатов. - СПб.: Лань, 2018. - 136 c. Асанов М. О., Баранский В. А., Расин В. В. — Дискретная математика: Графы, матроиды, алгоритмы: Учебное пособие. 2-е изд., испр. и доп. — СПб.: Издательство "Лань", 2010. — 368 с. Белотелов, Н.В. Сложность. Математическое моделирование. Гуманитарный анализ: Исследование исторических, военных, социально-экономических и политических процессов / Н.В. Белотелов, Ю.И. Бродский, Ю.Н. Павловский. - М.: КД Либроком, 2019. - 320 c. Волгина, О.А. Математическое моделирование экономических процессов и систем: Учебное пособие / О.А. Волгина, Н.Ю. Голодная, Н.Н. Одияко. - М.: КноРус, 2016. - 395 c. Жирков, А.М. Математическое моделирование систем и процессов: Учебное пособие / А.М. Жирков, Г.М. Подопригора, М.Р. Цуцунава. - СПб.: Лань КПТ, 2016. - 192 c. Катаргин, Н.В. Экономико-математическое моделирование: Учебное пособие / Н.В. Катаргин. - СПб.: Лань, 2018. - 256 c. Кормен, Томас Х., Лейзерсон, Чарльз И., Ривест, Рональд Л., Штайн Клиффорд Алгоритмы: построение и анализ, 2-е издание. Пер. с англ. — М.:Издательский дом "Вильямс", 2010. — 1296 с. Михалева, М.Ю. Математическое моделирование и количественные методы исследований в менеджменте: Учебное пособие / М.Ю. Михалева, И.В. Орлова. - М.: Вузовский учебник, 2019. - 320 c. Степанов, В.И. Экономико-математическое моделирование / В.И. Степанов. - М.: Academia, 2018. - 336 c. Яглом, И.М. Математические структуры и математическое моделирование / И.М. Яглом. - М.: Ленанд, 2018. - 144 c. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||



 0,8
0,8