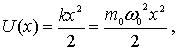1 Билет
1 вопрос
Интерференция светав оптике - это явление пространственного перераспределения светового потока, происходящее при наложении двух когерентных волн (если частота одинаковая и постоянная разность фаз, то волны когерентные или монохромные волны с постоянной рвзностью фаз); проявляется возникновением максимумов и минимумов интенсивности.
Интерференция света - опыт Юнга. Допустим, что свет от лампочки со светофильтpом, котоpый создает пpактически монохpоматический свет, пpоходит чеpез две узкие, pядом pасположенные щели, за котоpыми установлен экpан (pис. 1.7).
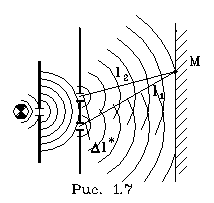
На экpане будет наблюдаться система светлых и темных полос - полос интеpфеpенции. В данном случае единая световая волна pазбивается на две, идущие от pазличных щелей. Эти две волны когеpентны между собой и пpи наложении дpуг на дpуга дают систему максимумов и минимумов интенсивности света в виде темных и светлых полос соответствующего цвета.
Интерференция света - условия max и min.
Условие максимума:
Если в оптической разности хода волн укладывается четное число полуволн или целое число волн, то в данной точке экрана наблюдается усиление интенсивности света (max).
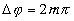 , где , где 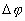 - pазность фаз складываемых волн. - pазность фаз складываемых волн.
Условие минимума:
Если в оптической разности хода волн укладывается нечетное число полуволн, то в точке минимум.
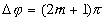
2 вопрос
Тепловое излучение происходит за счет внутренней энергии вещества и поэтому свойственно всем телам при любой температуре, отличной от 0 К.
Нагретые тела излучают электромагнитные волны. Это излучение осуществляется за счет преобразования энергии теплового движения частиц тела в энергию излучения.
2 билет
1 вопрос
Фотоэффе́кт — это испускание электронов веществом под действием света (и, вообще говоря, любого электромагнитного излучения). В конденсированных веществах (твёрдых и жидких) выделяют внешний и внутренний фотоэффект.
Законы фотоэффекта:
Формулировка 1-го закона фотоэффекта: количество электронов, вырываемых светом с поверхности металла за единицу времени на данной частоте, прямо пропорционально световому потоку, освещающему металл.
Согласно 2-ому закону фотоэффекта, максимальная кинетическая энергия вырываемых светом электронов линейно возрастает с частотой света и не зависит от его интенсивности.
3-ий закон фотоэффекта: для каждого вещества существует красная граница фотоэффекта, то есть минимальная частота светаν0(или максимальная длина волны λ0), при которой ещё возможен фотоэффект, и еслиν < ν0, то фотоэффект уже не происходит.
Теоретическое объяснение этих законов было дано в 1905 году Эйнштейном. Согласно ему, электромагнитное излучение представляет собой поток отдельных квантов (фотонов) с энергией hν каждый, где h — постоянная Планка. При фотоэффекте часть падающего электромагнитного излучения от поверхности металла отражается, а часть проникает внутрь поверхностного слоя металла и там поглощается. Поглотив фотон, электрон получает от него энергию и, совершая работу выхода, покидает металл: hν = Aout + We, где We — максимальная кинетическая энергия, которую может иметь электрон при вылете из металла.
3 билет
1 вопрос
Каждый элемент волнового фронта можно рассматривать, как центр вторичного возмущения, порождающего вторичные сферические волны, а результирующее световое поле в каждой точке пространства будет определяться интерференцией этих волн
2 вопрос
Комптоновское рассеивание- упругое рассеяние фотона на свободном электроне. К. р. определяет непрозрачность вещества для жёстких (высокоэнергичных) рентгеновских и гамма-лучей. Рассеяние фотона на покоящемся электроне в силу законов сохранения энергии и количества движения сопровождается уменьшением энергии фотона и передачей её электрону. Это явление было экспериментально Комптоном, исследовавшим рассеяние рентг. лучей в графите, и известно как эффект Комптона (комптон-эффект), или эффект отдачи.
6 билет
2 вопрос
КОНТАКТНЫЕ ЯВЛЕНИЯ В ПОЛУПРОВОДНИКАХ - неравновесные электронные явления, возникающие при прохождении электрич. тока через контакт полупроводника с металлом или электролитом или через контакт двух различных полупроводников либо через границу двух областей одного и того же полупроводника с разным типом носителей заряда и разной их концентрацией.
Граница соприкосновения двух полупроводников, один из которых имеет электронную, а другой — дырочную проводимость, называется электронно-дырочным переходом (или p-n-переходом)
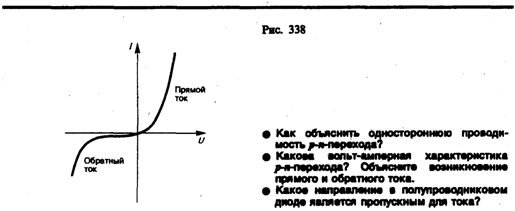
На рис. 338 представлена вольт-амперная характеристика p-n-перехода. Как уже указывалось, при пропускном (прямом) напряжении внешнее электрическое поле способствует движению основных носителей тока к границе p-n-переходаВ результате толщина контактного слоя уменьшается. Соответственно уменьшается и сопротивление перехода (тем сильнее, чем больше напряжение), а сила тока становится большой (правая ветвь на рис. 338). Это направление тока называетсяпрямым.
При запирающем (обратном) напряжении внешнее электрическое поле препятствует движению основных носителей тока к границе p-n-перехода и способствует движению неосновных носителей тока, концентрация которых в полупроводниках невелика. Это приводит к увеличению толщины контактного слоя, обедненного основными носителями тока. Соответственно увеличивается и сопротивление перехода. Поэтому в данном случае через p-n-переход протекает только небольшой ток (он называется обратным), полностью обусловленный неосновными носителями тока (левая ветвь рис. 338). Быстрое возрастание этого тока означает пробой контактного слоя и его разрушение. При включении в цепь переменного тока p-n-переходы действуют как выпрямители.
7 билет
2 вопрос
При образовании твердого тела в смысле кристаллизации атомов в жесткую структуру каждый энергетический электронный уровень в атомах расщепляется на ряд близких подуровней, объединенных в энергетическую полосу или зону. Все электроны, находящиеся в данной энергетической полосе, обладают очень близкими энергиями.
валентная зона — размытый на подуровни внешний слой электронной оболочки атомов, который у большинства веществ не заполнен. Поскольку внешний слой не насыщен электронами, в нем всегда имеются свободные подуровни, которые могут занять электроны из внешней оболочки соседних атомов. Слой, в котором имеются свободно перемещающиеся электроны, принято называть зоной проводимости.Запрещённая зона — область значений энергии, которыми не может обладать электрон в идеальном (бездефектном) кристалле. Ширина запрещённой зоны — это ширина энергетического зазора между дном зоны проводимости и потолком валентной зоны, в котором отсутствуют разрешённые состояния для электрона.
Проводник, представляет собой вещество с частично заполненной зоной валентных электронов, внутри которой электроны имеют значительную свободу перемещения от атома к атому. Наконец,полупроводники — это кристаллические вещества с заполненной валентной зоной, и в этом они подобны изоляторам, однако разность энергий между валентным уровнем и следующим, проводящим энергетическим уровнем у них настолько незначительна, что электроны преодолевают ее при обычных температурах чисто в силу теплового движения.
8 билет
1 вопрос
Закон прямолинейного распространения света : в прозрачной однородной среде свет распространяется по прямым линиям. В связи с законом прямолинейного распространения света появилось понятие световой луч, которое имеет геометрический смысл как линия, вдоль которой распространяется свет. Реальный физический смысл имеют световые пучки конечной ширины. Световой луч можно рассматривать как ось светового пучка. Поскольку свет, как и всякое излучение, переносит энергию, то можно говорить, что световой луч указывает направление переноса энергии световым пучком. Также закон прямолинейного распространения света позволяет объяснить, как возникают солнечные и лунные затмения.
2 вопрос
Спонтанное и индуцированное излучение
Атомы и молекулы находятся в определенных энергетических состояниях, находятся на определенных энергетических уровнях. Для того, чтобы изолированный атом изменил свое энергетическое состояние, он должен либо поглотить фотон (получить энергию) и перейти на более высокий. энергетический уровень, либо излучить фотон и перейти в более низкое энергетическое состояние
Если в области, где находится возбужденный атом отсутствует электромагнитное поле, то процесс перехода атома в нижнее состояние, сопровождаемый излучением фотона и характеризуемый постоянной составляющей вероятности перехода, называется спонтанным излучением.
Спонтанное излучение не когерентно так как при этом различные атомы излучают независимо друг от друга.
Интенсивность спонтанного излучения убывает по экспонентциальному закону.
Схема действия квантового генератора приведена на рис. 362. Пространство между зеркалами заполнено активной средой, т. е. средой, содержащей больше возбужденных атомов, чем невозбужденных. Среда усиливает проходящий через нее свет, начало которому дает спонтанное излучение одного из атомов. Большое усиление достигается, когда угол a очень мал так что свет испытывает много отражений и все лучи накладываются, усиливая друг друга. Излучение генератора выходит наружу через зеркало 2. Такой генератор излучает свет с частотой
n=(W—W')/h, где W — W' — разность энергий уровней,
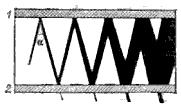
Рис. 362. Схема действия оптического квантового генератора: 1, 2 — плоскопараллельные зеркала; зеркало 2 слегка прозрачно. (Угол a на рисунке сильно преувеличен.)
участвующих в процессе. Построены генераторы и усилители, действующие в диапазоне коротких радиоволн, инфракрасного, видимого и ультрафиолетового света.
Так как при излучении света атомы переходят с верхнего уровня на нижний, генерация приводит к быстрому уменьшению избытка населенности верхнего уровня. Если не восполнять уменьшение, то действие генератора прекратится, как только избыточная населенность снизится до некоторого предельного уровня.
9 билет
1 вопрос
Простейшим для расчета и практически очень важным случаем является фраунгоферова дифракция на длинной прямоугольной щели (Дифракция Фраунгофера на щели). Ширину щели обозначим через b, ее длину будем считать бесконечной. Пусть на щель нормально падает плоская монохроматическая волна (рис. 5.7.1). Световое поле за щелью найдется по принципу Гюйгенса как результат интерференции когерентных вторичных волн, исходящих из различных точек волнового фронта на щели. Вторичные волны, излучаемые полоской волнового фронта ширины dx, параллельной щели, складываясь, дают цилиндрическую волну, осью которой является эта полоска. Зависимость этой волны от направления ее распространения, определяемого углом j должен предполагаться малым.Однако необходимо учесть разности фаз между волнами, исходящими из различных полосок. Разумеется, речь идет о фазах колебаний на бесконечном расстоянии от щели. Волна, исходящая из dx под углом j, опережает по фазе волну того же направления, исходящую из середины щели О, на kx sinj.
Поэтому результирующее поле в бесконечности, создаваемое всей щелью, представиться интегралом
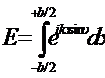
Здесь опущены все множители, не являющиеся на относительное распределение волнового поля по направлениям. Вычислив интеграл, получим
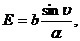
Где введено обозначение
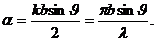
Отсюда для распределения интенсивности света по направлениям найдем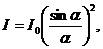
Где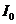 - интенсивность в направлении падающей волны. Обе функции обращаются в максимум, равной единице, при a=0. При - интенсивность в направлении падающей волны. Обе функции обращаются в максимум, равной единице, при a=0. При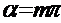 , где m=1,2 они равны 0. Между двумя соседними минимумами располагаются максимумы различных порядков. Их положения определяются трансцендентным уравнением a cos-sina=0. Практически можно считать, что максимумы располагаются посередине между соседними минимумами. , где m=1,2 они равны 0. Между двумя соседними минимумами располагаются максимумы различных порядков. Их положения определяются трансцендентным уравнением a cos-sina=0. Практически можно считать, что максимумы располагаются посередине между соседними минимумами.
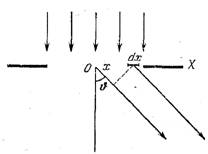
Рис. 5.7.1. Дифракция Фраунгофера на щели
Дифракция Фраунгофера на дифракционной решетке. Условия минимумов и максимумов.
Большое практическое значение имеет дифракция, наблюдаемая при прохождении света через одномерную дифракционную решетку - систему параллельных щелей равной ширины, лежащих в одной плоскости и разделенных равными по ширине непрозрачными промежутками. Рассматривая дифракцию Фраунгофера на щели, мы видели, что распределение интенсивности на экране определяется направлением дифрагированных лучей. Это означает, что перемещение щели параллельно самой себе влево или вправо не изменит дифракционной картины. Следовательно, если перейти от одной щели ко многим (к дифракционной решетке), то дифракционные картины, создаваемые каждой щелью в отдельности, будут одинаковыми.
Рассмотрим дифракционную решетку. На рис. 7.1 для наглядности показаны только две соседние щели MN и CD. Бели ширина каждой щели равна а, а ширина непрозрачных участков между щелями b, то величина d=a+b называется постоянной (периодом) дифракционной решетки. Пусть плоская монохроматическая волна падает нормально к плоскости решетки. Так как щели находятся друг от друга на одинаковых расстояниях, то разности хода лучей, идущих от двух соседних щелей, будут для данного направления 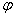 одинаковы в пределах всей дифракционной решетки: одинаковы в пределах всей дифракционной решетки: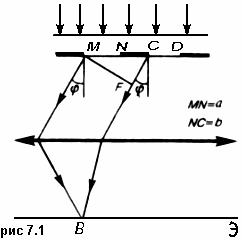
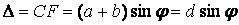 (7.1) (7.1)
Очевидно, что в тех направлениях, в которых ни одна из щелей не распространяет свет, он не будет распространяться и при двух щелях, т. е. прежние (главные) минимумы интенсивности будут наблюдаться в направлениях, определяемых условием ((6.2) 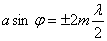 (m=1,2,3,…)): (m=1,2,3,…)):
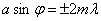 (m = 1, 2, 3, ...). (7.2) (m = 1, 2, 3, ...). (7.2)
Кроме того, вследствие взаимной интерференции световых лучей, посылаемых двумя щелями, в некоторых направлениях они будут гасить друг друга, т. е. возникнут дополнительные минимумы. Очевидно, что эти дополнительные минимумы будут наблюдаться в тех направлениях, которым соответствует разность хода лучей 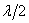 , , 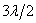 , ..., посылаемых, например, от крайних левых точек М и С обеих щелей. Таким образом, с учетом (7.1) условие дополнительных минимумов: , ..., посылаемых, например, от крайних левых точек М и С обеих щелей. Таким образом, с учетом (7.1) условие дополнительных минимумов:
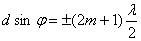 (m = 1, 2, 3, ...) (m = 1, 2, 3, ...)
Наоборот, действие одной щели будет усиливать действие другой, если
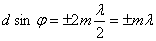 (m=0, 1, 2, ...), (7.3) (m=0, 1, 2, ...), (7.3)
т. е. выражение (7.3) задает условие главных максимумов.
т. е. между двумя главными максимумами располагается один дополнительный минимум. Аналогично можно показать, что между каждыми двумя главными максимумами при трех щелях располагается два дополнительных минимума, при четырех щелях - три и т. д.
10 билет
2 вопрос
Волнова́я фу́нкция, или пси-функция 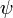 — комплекснозначная функция, используемая в квантовой механике для описания чистого состояния системы. Является коэффициентом разложения вектора состояния по базису (обычно координатному): — комплекснозначная функция, используемая в квантовой механике для описания чистого состояния системы. Является коэффициентом разложения вектора состояния по базису (обычно координатному):
Волновая функция 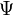 по своему смыслу должна удовлетворять так называемому условию нормировки, например, в координатном представлении имеющее вид: по своему смыслу должна удовлетворять так называемому условию нормировки, например, в координатном представлении имеющее вид:
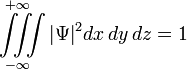
Это условие выражает тот факт, что вероятность обнаружить частицу с данной волновой функцией где-либо во всём пространстве равна единице. В общем случае интегрирование должно производиться по всем переменным, от которых зависит волновая функция в данном представлении
Физический смысл приписывается квадрату её модуля 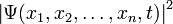 , который интерпретируется как плотность вероятности , который интерпретируется как плотность вероятности 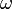 (для дискретных спектров — просто вероятность) обнаружить систему в положении, описываемом координатами (для дискретных спектров — просто вероятность) обнаружить систему в положении, описываемом координатами 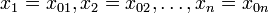 в момент времени в момент времени 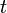 : :
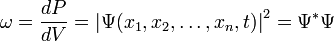 . .
Тогда в заданном квантовом состоянии системы, описываемом волновой функцией 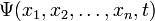 , можно рассчитать вероятность , можно рассчитать вероятность 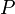 того, что частица будет обнаружена в любой области пространства конечного объема того, что частица будет обнаружена в любой области пространства конечного объема 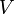 : : 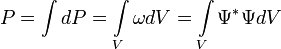 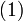 . .
14 билет
2 вопрос
Энергетический спектр (закон дисперсии) — зависимость энергии частицы от импульса. Для свободной частицы закон дисперсии зависит квадратично от импульса.
Как известно, гармоническим осциллятором называется система, способная совершать гармонические колебания. Рассмотрим одномерный гармонический осциллятор, совершающий колебания вдоль оси 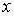 под действием возвращающей квазиупругой силы под действием возвращающей квазиупругой силы 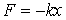 . Потенциальная энергия такого осциллятора имеет вид . Потенциальная энергия такого осциллятора имеет вид
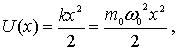
|
(4.77)
|
где 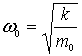 - собственная частота классического гармонического осциллятора. Таким образом, квантово-механическая задача о гармоническом осцилляторе сводится к задаче о движении частицы в параболической потенциальной яме (4.77) . - собственная частота классического гармонического осциллятора. Таким образом, квантово-механическая задача о гармоническом осцилляторе сводится к задаче о движении частицы в параболической потенциальной яме (4.77) .
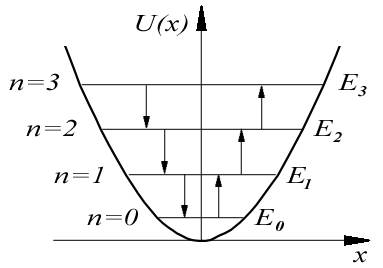
Отметим, что энергетические уровни гармонического осциллятора, в отличие, например, от случая прямоугольной потенциальной ямы, являются эквидистантными, т.е. расположены на одинаковом энергетическом расстоянии 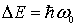 друг от друга (рис.4.25) . друг от друга (рис.4.25) .
20 билет
1 вопрос
Фотоэффектом называют процесс испускания электронов телами, на которые действует свет. В твёрдых и жидких телах выделяют внешний и внутренний фотоэффект.
В работе Эйнштейна содержалась важная новая гипотеза. Ученый выдвинул гипотезу о том, что свет существует только в виде квантованных порций. Из представления о свете как о фотонах следует формула Эйнштейна для фотоэффекта:
h ν = Aion+ Aout+ mv2/2,
Aion - работа по ионизации атомов вещества,
Aout - работа необходимая для выхода электрона из вещества,
m - кинетическая энергия вылетающего электрона,
ν - частота падающего фотона с энергией
h - постоянная Планка.
МНОГОФОТОННЫЙ ФОТОЭФФЕКТ - термин, объединяющий ряд фотоэлектрических явлений, при к-рых изменение электропроводности, возникновение эдс или эмиссия электронов происходят вследствие поглощения электроном вещества (т. е. в связанном состоянии) двух или более фотонов в одном элементарном акте. Многофотонный вариант отличается тем, что электроны вещества приобретают необходимую энергию в процессе многофотонного поглощения, в то время как при "обычном" фотоэффекте требуемое возбуждение электронов достигается за счёт однофотонного поглощения. Это обстоятельство обусловливает гл. особенности M. ф.: 1) M. ф. наблюдается при достаточно высоких интенсивностях / падающего излучения, достижимых лишь с помощью лазеров; 2) величина фотоотклика вещества (фотоэдс, фототек) при M. ф. пропорциональна /т, где т - порядок фотоэффекта, т. е. число фотонов, поглощаемых в одном акте; 3) зависимость M. ф. от частоты излучения отражает спектральные характеристики многофотонного поглощения.
21 билет
2 вопрос
Во́лны де Бро́йля — волны, связанные с любыми микрочастицами и отражающие их волновую природу. В 1924 году[1] французский физик Луи де Бройль высказал гипотезу о том, что установленный ранее[1] для фотонов корпускулярно-волновой дуализмприсущ всем частицам — электронам, протонам, атомам и так далее, причём количественные соотношения между волновыми и корпускулярными свойствами частиц те же, что и для фотонов. Таким образом, если частица имеет энергию E и импульс, абсолютное значение которого равно p, то с ней связана волна, частота которой ν = E / h и длина волны λ = h / p, где h — постоянная Планка.
Для частиц не очень высокой энергии, движущихся со скоростью 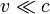 (скорости света), импульс равен (скорости света), импульс равен 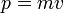 (где (где 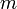 — масса частицы), и — масса частицы), и 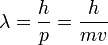 . Следовательно, длина волны де Бройля тем меньше, чем больше масса частицы и её скорость. Подтвержденная на опыте идея де Бройля о двойственной природе микрочастиц — корпускулярно-волновом дуализме — принципиально изменила представления об облике микромира. Поскольку всем микрообъектам (за ними сохраняется термин «частица») присущи и корпускулярные, и волновые свойства, то, очевидно, любую из этих «частиц» нельзя считать ни частицей, ни волной в классическом понимании. Возникла потребность в такой теории, в которой волновые и корпускулярные свойства материи выступали бы не как исключающие, а как взаимно дополняющие друг друга. В основу такой теории — волновой, или квантовой, механики — и легла концепция де Бройля. Это отражается даже в названии «волновая функция» для величины, описывающей в этой теории состояние системы. Квадрат модуля волновой функции определяет вероятность состояния системы, и поэтому о волнах де Бройля часто говорят[3]как о волнах вероятности (точнее, амплитуд вероятности). Для свободной частицы с точно заданным импульсом p (и энергией . Следовательно, длина волны де Бройля тем меньше, чем больше масса частицы и её скорость. Подтвержденная на опыте идея де Бройля о двойственной природе микрочастиц — корпускулярно-волновом дуализме — принципиально изменила представления об облике микромира. Поскольку всем микрообъектам (за ними сохраняется термин «частица») присущи и корпускулярные, и волновые свойства, то, очевидно, любую из этих «частиц» нельзя считать ни частицей, ни волной в классическом понимании. Возникла потребность в такой теории, в которой волновые и корпускулярные свойства материи выступали бы не как исключающие, а как взаимно дополняющие друг друга. В основу такой теории — волновой, или квантовой, механики — и легла концепция де Бройля. Это отражается даже в названии «волновая функция» для величины, описывающей в этой теории состояние системы. Квадрат модуля волновой функции определяет вероятность состояния системы, и поэтому о волнах де Бройля часто говорят[3]как о волнах вероятности (точнее, амплитуд вероятности). Для свободной частицы с точно заданным импульсом p (и энергией 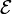 ), движущейся вдоль оси x, волновая функция имеет вид[1]: ), движущейся вдоль оси x, волновая функция имеет вид[1]:
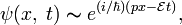
где 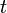 — время, — время, 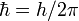 . .
В этом случае 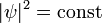 , то есть вероятность обнаружить частицу в любой точке одинакова. , то есть вероятность обнаружить частицу в любой точке одинакова.
22 билет
1 вопрос
Проводилось исследование отражения электронов от монокристалла никеля. Установка включала в себя монокристалл никеля, сошлифованный под углом, и установленный на держателе. На плоскость шлифа направлялся перпендикулярно пучок монохроматических электронов. Скорость электронов определялась напряжением 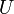 на электронной пушке: на электронной пушке:
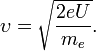
Под углом 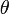 к падающему пучку электронов устанавливался цилиндр Фарадея, соединённый с чувствительным гальванометром. По показаниям гальванометра определялась интенсивность отражённого от кристалла электронного пучка. Вся установка находилась в вакууме. к падающему пучку электронов устанавливался цилиндр Фарадея, соединённый с чувствительным гальванометром. По показаниям гальванометра определялась интенсивность отражённого от кристалла электронного пучка. Вся установка находилась в вакууме.
В опытах измерялась интенсивность рассеянного кристаллом электронного пучка в зависимости от угла рассеяния 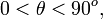 от азимутального угла от азимутального угла 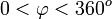 , от скорости , от скорости 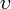 электронов в пучке. электронов в пучке.
. При различных значениях углов и скоростей, в отражённых лучах наблюдаются максимумы и минимумы интенсивности. Условие максимума:
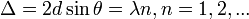
Здесь 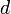 — межплоскостное расстояние. — межплоскостное расстояние.
Таким образом наблюдалась дифракция электронов на кристаллической решётке монокристала.
В 1928 году Г. П. Томсон и независимо от него П. С. Тартаковский получили дифракционную картину при прохождении электронного пучка через металлическую фольгу Г. П. Томсон пропускал тонкий монохроматический пучок быстрых электронов сквозь монокристаллическую фольгу толщиной ∼10-5 см. П. С. Тартаковский использовал поток менее быстрых электронов.
Пучок электронов, ускоренный разностью потенциалов, проходил через тонкую металлическую фольгу и попадал на фотопластинку. Электрон при ударе о фотопластинку оказывал на нее такое же действие, как и фотон. Все электроны укладывались на фотопластинке точно по кругу, то есть образовывалась дифракционная картина Сходство с полученной в таких же условиях рентгенограммой, было идеальным.
Для частиц не очень высокой энергии, движущихся со скоростью 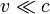 (скорости света), импульс равен (скорости света), импульс равен 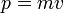 (где (где 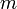 — масса частицы), и — масса частицы), и 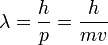 . Следовательно, длина волны де Бройля тем меньше, чем больше масса частицы и её скорость . Следовательно, длина волны де Бройля тем меньше, чем больше масса частицы и её скорость
2 вопрос
Интерференцию света можно объяснить, рассматривая интерференцию волн Необходимым условием интерференции волн является их когерентность, т. е. согласованное протекание во времени и пространстве нескольких колебательных или волновых процессов. Этому условию удовлетворяют монохроматические волны — неограниченные в пространстве волны одной определенной и строго постоянной частоты. Так как ни один реальный источник не дает строго монохроматического света, то волны, излучаемые любыми независимыми источниками света, всегда некогерентны.
Оптической длиной пути между точками А и В прозрачной среды; расстояние, на которое свет (Оптическое излучение) распространился бы в вакууме за время его прохождения от А до В. Оптической длиной пути в однородной среде называется произведение расстояния, пройденного светом в среде с показателем преломления n, на показатель преломления:
l = nS
Для неоднородной среды необходимо разбить геометрическую длину на столь малые промежутки, что можно было бы считать на этом промежутке показатель преломления постоянным:
dl = nds
Полная оптическая длина пути находится интегрированием:
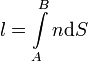
Оптическая разность хода - это разность оптических длин путей световых волн, имеющих общие начальную и конечную точки. В кристаллических анизотропных средах разность хода возникает из-за разных скоростей двух лучей в направлении, отличном от оптической оси
1.Для разделения световой волны используют двойную призму (бипризму) с малым преломляющим углом 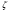 . Источником света является ярко освещенная щель S, параллельная преломляющему ребру бипризмы. В силу малости преломляющего угла бипризмы (несколько угловых минут ) все лучи отклоняются на один и тот же угол . Источником света является ярко освещенная щель S, параллельная преломляющему ребру бипризмы. В силу малости преломляющего угла бипризмы (несколько угловых минут ) все лучи отклоняются на один и тот же угол 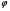 независимо от угла падения, при этом отклонение происходит в сторону основания каждой из призм, составляющих бипризму. В результате образуются две когерентные волны, виртуально исходящих из мнимых источников независимо от угла падения, при этом отклонение происходит в сторону основания каждой из призм, составляющих бипризму. В результате образуются две когерентные волны, виртуально исходящих из мнимых источников 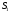 и и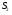 , лежащих в одной плоскости с реальным источником , лежащих в одной плоскости с реальным источником Смещение изображений источника Смещение изображений источника 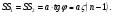 Тогда расстояние между мнимыми источниками Тогда расстояние между мнимыми источниками  Ширина интерференционной полосы Ширина интерференционной полосы 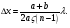 Область перекрытия когерентных пучков, исходящих из двух мнимых копий источника S, равна Область перекрытия когерентных пучков, исходящих из двух мнимых копий источника S, равна 
2.В установке бизеркала Френеля две когерентные волны получают при отражении от двух зеркал, плоскости которых образуют двугранный угол  ,где ,где 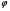 - очень малый угол. Источник – узкая освещенная щель - очень малый угол. Источник – узкая освещенная щель 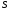 , параллельная грани двугранного угла. Отраженные от зеркал пучки падают на экран, и в области перекрытия возникает интерференционная картина в виде полос, параллельных щели. Как и в любой системе плоских зеркал, все три источника (реальный и два мнимых) находятся на одинаковом расстоянии от ребра двугранного угла, то есть на окружности с центром в ребре. При повороте зеркала на угол , параллельная грани двугранного угла. Отраженные от зеркал пучки падают на экран, и в области перекрытия возникает интерференционная картина в виде полос, параллельных щели. Как и в любой системе плоских зеркал, все три источника (реальный и два мнимых) находятся на одинаковом расстоянии от ребра двугранного угла, то есть на окружности с центром в ребре. При повороте зеркала на угол 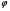 световой луч смещается на световой луч смещается на  , поэтому , поэтому  Используя малость угла Используя малость угла 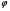 ,получим расстояние между мнимыми источниками ,получим расстояние между мнимыми источниками 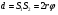 и ширину интерференционной полосы и ширину интерференционной полосы 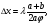 где где  Хотя при отражении от зеркала происходит фазовый сдвиг Хотя при отражении от зеркала происходит фазовый сдвиг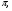 дополнительной разности фаз не возникает, так как сдвигаются фазы обоих пучков. дополнительной разности фаз не возникает, так как сдвигаются фазы обоих пучков.
23 билет
2 вопрос
Закон Брюстера — закон оптики, выражающий связь показателя преломления с таким углом, при котором свет, отражённый от границы раздела, будет полностью поляризованным в плоскости, перпендикулярной плоскости падения, а преломлённый луч частично поляризуется в плоскости падения, причем поляризация преломленного луча достигает наибольшего значения. Легко установить, что в этом случае отраженный и преломленный лучи взаимно перпендикулярны. Соответствующий угол называется углом Брюстера.
Закон Брюстера: 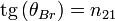 , где n21 — показатель преломления второй среды относительно первой, θBr — угол падения (угол Брюстера). , где n21 — показатель преломления второй среды относительно первой, θBr — угол падения (угол Брюстера).
|
 Скачать 162.04 Kb.
Скачать 162.04 Kb.