|
|
Вероятность 9. 7. распределения вероятностей непрерывных случайных величин равномерное распределение|
ЛЕКЦИЯ 9
Распределения вероятностей непрерывных случайных величин. Равномерное распределение. Показательное распределение и его числовые характеристики. Функция надежности. Характеристическая функция.
7.1. Равномерное распределение
На практике встречаются случайные величины, о которых заранее известно, что они могут принять какое-либо значение в строго определенных границах, причем в этих границах все значения случайной величины имеют одинаковую вероятность (т.е. обладают одной и той же плотностью вероятности).
К подобным случайным величинам относится погрешность округления, например при снятии показаний с измерительных приборов, если производится округление до ближайшего целого деления. Тогда ошибка округления есть случайная величина, которая может принимать с постоянной плотностью вероятности любое значение между двумя соседними целыми делениями. Например, мы записываем значение напряжения 220 В, хотя реально это значение находится, допустим, между 215 и 225 В.
Распределение вероятностей называют равномерным, если на интервале, которому принадлежат все возможные значения случайной величины, плотность распределения постоянна:

Так как
 , ,
то C=1/(b–a). Таким образом, плотность вероятности равномерного распределения имеет вид
 (7.1) (7.1)
Построим функцию распределения F(x) для равномерного распределения:
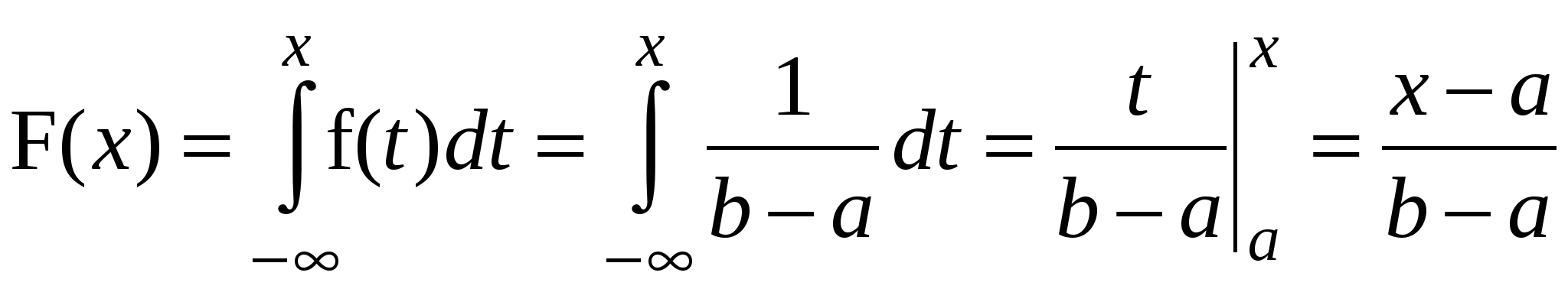 . .
Отметим, что при x<a функция F(x)=0 и при x>b функция F(x)=1.

 
Рис. 7.1
(7.2)
Вычислим основные числовые характеристики равномерного распределения. Математическое ожидание:
 . .
Таким образом, математическое ожидание случайной величины, распределенной равномерно на отрезке [a,b], совпадает с серединой этого отрезка.
Дисперсию находим по формуле
 . .
Так как рассматриваемое распределение симметрично относительно математического ожидания, то для него все центральные моменты, имеющие нечетный порядок, равны нулю. Следовательно, коэффициент асимметрии такого распределения равен нулю:
 . .
Вычислим теперь эксцесс равномерного распределения
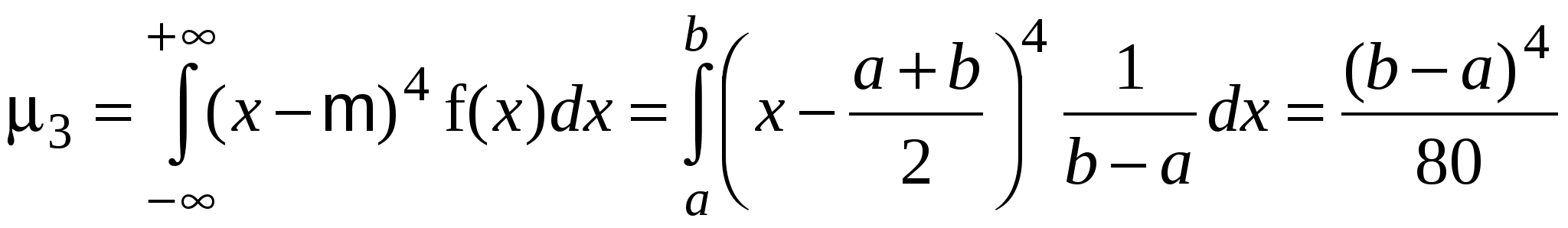 . .
Тогда
 . .
Вопрос: Что можно сказать о медиане и моде равномерного распределения?
7.2. Показательное распределение
Непрерывная случайная величина X называется распределенной по показательному (экспоненциальному) закону, если ее плотность распределения вероятностей задается формулой
 (7.3) (7.3)
 
Рис. 7.2
Показательное распределение часто встречается в теории массового обслуживания (например, X – время ожидания при техническом обслуживании или длительность телефонных разговоров, ежедневно регистрируемых на телефонной станции) и в теории надежности (например, X – срок службы радиоэлектронной аппаратуры).
Найдем функцию распределения показательного распределения:
 . .
Итак
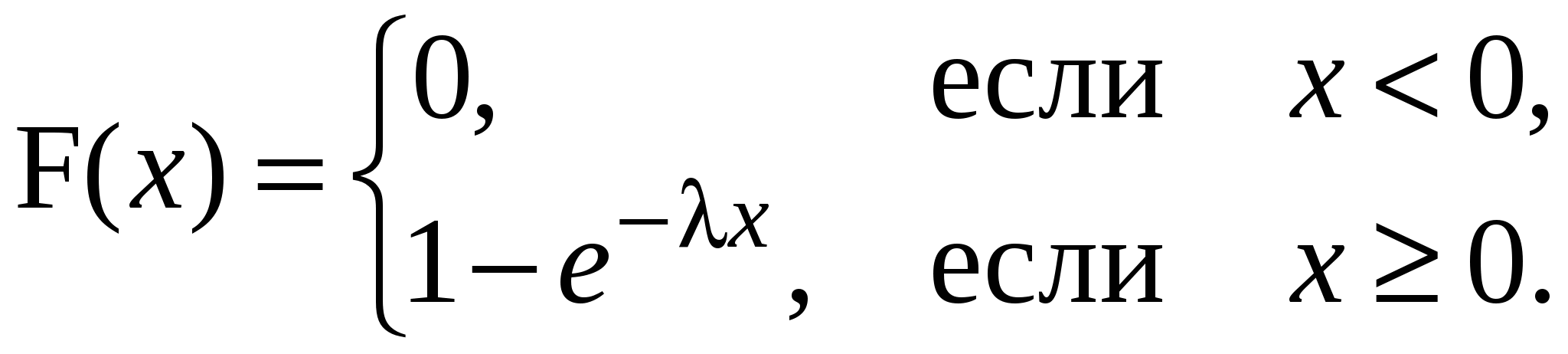 (7.4) (7.4)
График плотности распределения и функции распределения для показательного распределения показаны на рис. 7.2.
Пусть T – непрерывная случайная величина, означающая длительность времени безотказной работы устройства. Функцией надежностиR(t) называется функция, определяющая вероятность безотказной работы устройства в течение времени не меньшей t:
 (7.5) (7.5)
Поскольку F(t)=P(T<t), то
 . .
Если случайная величина имеет показательное распределение, то
 (7.6) (7.6)
где – интенсивность отказов, т.е. среднее число отказов в единицу времени.
Показательное распределение обладает весьма важным свойством, характерным только для этого распределения: для любых чисел x1и x2выполняется равенство
 (7.7) (7.7)
Следствием этого свойства является т.н. свойство "отсутствия последействия", т.е. вероятность безотказной работы устройства на некотором интервале не зависит от времени предшествующей работы, а зависит только от его длительности.
Действительно, пусть A – безотказная работа на интервале (0,t0), B – безотказная работа на интервале (t0,t0+t). Тогда AB – безотказная работа на интервале (0,t0+t). Поскольку длительности времен безотказной работы для событий A, B и AB, соответственно, равны t0, t, t0+t, то

Найдем условную вероятность того, что устройство будет работать безотказно на интервале (t0,t0+t) при условии, что он уже пробовал безотказно в течение предшествующего интервала (0,t0):
 . .
В результате получилось, что P(B)=PA(B), т.е. в случае показательного закона вероятность безотказной работы устройства "в прошлом" не сказывается на величине вероятности его безотказной работы "в ближайшем будущем".
Например, при допущении метеориты распределены равномерно в пространстве и во времени, вероятность попадания метеорита в космический корабль не зависит от того, попали или нет в него метеориты до начала рассматриваемого интервала времени. Отсюда следует, что случайные моменты попадания метеоритов в космический корабль распределены по показательному закону.
Можно доказать и обратное утверждение: если случайная величина обладает свойством отсутствия последействия, то она обязана иметь показательное распределение. Таким образом, отсутствие последействия является характеристическим свойством показательного распределения.
Отметим, что показательное распределение тесно связано с распределением Пуассона, а именно: если времена между последовательными наступлениями некоторого события представляют собой независимые показательно распределенные (с одним и тем же параметром ) случайные величины, то число наступлений этого события за время t распределено по закону Пуассона с параметром t. Отметим также, что дискретным аналогом показательного распределения является геометрическое распределение.
Найдем числовые характеристики показательного распределения: математическое ожидание:
 , ,
дисперсию:
 , ,
среднее квадратичное отклонение:
 . .
Таким образом, для показательного распределения характерно, среднее квадратичное отклонение численно равно математическому ожиданию. Нетрудно убедится, что коэффициент асимметрии и эксцесс для показательного распределения являются постоянными величинами:
A = 2, E = 9.
Пример 7.1. Время распределения состава через горку –случайная величина, подчиненная показательному закону. Пусть =6 – среднее число поездов, которые горка может расформировать за 1 ч. Определить вероятность того, что время расформирования состава: а) меньше 30 мин; б) больше 10 мин, но меньше 40 мин.
Решение. а) Здесь нужно использовать функцию распределения показательного распределения F(t)=P(T<t)=1–e–t. Вероятность того, что расформирование состава займет менее 30 мин = 0,5 ч есть
 . .
б) Здесь нужно использовать формулу
 . .
Вероятность того, что расформирование состава займет больше =
10 мин =1/6 ч, но меньше =40 мин = 2/3 ч, равно

Пример 7.2. Вероятность безотказной работы радиоэлемента распределена по показательному закону  (t>0). найти вероятность того, что радиоэлемент проработает безотказно не менее 50 ч. (t>0). найти вероятность того, что радиоэлемент проработает безотказно не менее 50 ч.
Решение. Используя функцию надежности R(t)=e–t, получим

7.3*. Характеристическая функция
Мы говорили в предыдущих лекциях, что в теории вероятностей широко используются методы различных разделов математического анализа. Простейшие методы дифференциального и интегрального исчислений мы уже использовали при решении различных задач теории вероятностей. Сейчас мы познакомимся с методом характеристических функций, который в математическом анализе известен под именем преобразования Фурье.
Характеристической функцией случайной величины называется математическое ожидание случайной величины eit.
Если есть НСВ с плотностью распределения f(x), то характеристическая функция будет иметь вид
 (7.8) (7.8)
Из этой формулы видно, что характеристическая функция отличается от преобразования Фурье плотности распределения только лишь множителем  . .
Если есть ДСВ, то характеристическая функция будет иметь вид
 . (7.9) . (7.9)
Перечислим некоторые свойства характеристических функций:
1) f(0) = 1, |f(t)| < 1.
2) Если =a+b, то
 . .
3) Если 1 и 2 – независимые случайные величины и =1+2, то
 . .
Данное свойство является тем основным свойством, благодаря которому характеристические функции нашли такое широкое применение в теории вероятностей. При суммировании независимых случайных величин их плотности распределения преобразуются по формуле свертки. Но формула свертки весьма неудобна для исследования, гораздо проще заменить ее простым перемножением характеристических функций.
4) Если случайная величина имеет абсолютный момент n-го порядка, то характеристическая функция дифференцируема n раз, причем для kn
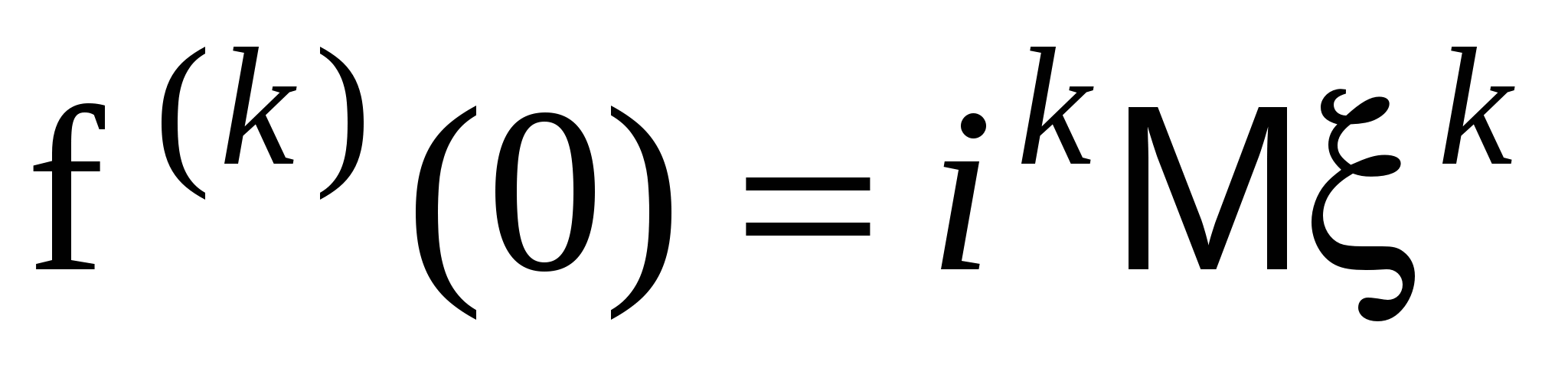
Используя свойство 4 можно получить выражения для математического ожидания и дисперсии, которые выражаются через производные логарифма характеристической функции. Если
 , (7.10) , (7.10)
то
 (7.11) (7.11)
Важнейшей особенностью характеристической функции f(t) является тот факт, что она однозначно определяет функцию распределения F(x). А именно справедлива следующая формула:
Теорема обращения. Для любых точек непрерывности x1и x2функции распределения F(x)
 . .
Отметим, что по своей сути формула обращения представляет собой разновидность обратного преобразования Фурье. Таким образом, определение характеристической функции вместе с формулой обращения устанавливает взаимно однозначное соответствие между функцией распределения и характеристической функцией.
Замечание. Между характеристическими и производящими функциями одной и той же случайной величины существует взаимосвязь, которая выражается равенством  . Отметим, что производящая функция, по сути дела, обладает теми же свойствами, что и характеристическая функция, однако с производящими функциями проще обращаться. . Отметим, что производящая функция, по сути дела, обладает теми же свойствами, что и характеристическая функция, однако с производящими функциями проще обращаться.
Пример__7.4.'>Пример__7.3.'>Пример 7.3. Найти характеристическую функцию биномиального распределения.
Решение. Пусть – ДСВ, подчиненная биномиальному закону распределения и принимающая значения 0, 1, 2, … n. Тогда характеристическая функция будет иметь вид
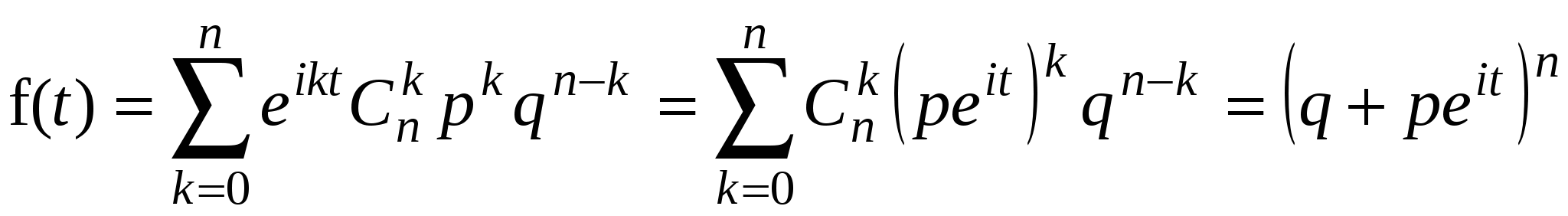 . .
Используя характеристическую функцию, найдем математическое ожидание и дисперсию биномиального распределения. Поскольку
 , ,
 , ,  , ,
то, как и следовало ожидать,

Пример 7.4. Найти характеристическую функцию распределения Пуассона.
Решение. Пусть – ДСВ, подчиненная закону распределения Пуассона и принимающая значения 0, 1, 2, … n. Тогда характеристическая функция будет иметь вид
 . .
Отсюда, в частности следует, что если =1+2, то ее функция распределения будет иметь вид
 . .
В силу взаимно однозначного соответствия между функцией распределения и характеристической функцией случайная величина распределена по закону Пуассона с параметрами 1+2.
Пример 7.5. Найти характеристическую функцию показательного распределения.
Решение. Пусть – НСВ, подчиненная показательному закону распределения. Тогда характеристическая функция будет иметь вид
 . .
Вычислим начальный момент n-го порядка случайной величины , распределенной по показательному закону. Воспользовавшись свойством 4, получим
 . . |
|
|
 Скачать 0.54 Mb.
Скачать 0.54 Mb.

 (7.1)
(7.1)



