ВычМат лаба1. Лаба1.отчет. Аппроксимация дискретных данных методом наименьших

• Название: Аппроксимация дискретных данных методом наименьших
• Анкор: ВычМат лаба1
• Дата: 27.09.2022
• Размер: 0.59 Mb.
• Имя файла: Лаба1.отчет.docx
• Тип: Отчет; #699020

Санкт-петербургский Политехнический университет Петра Великого

Институт материалов, машиностроения и транспорта

Высшая школа машиностроения
ОТЧЕТ
По лабораторной работе №1

Дисциплина: Вычислительная математика

Тема: Аппроксимация дискретных данных методом наименьших

квадратов

(Вариант 7)

Студент группы 3331505/00001 А. Ю. Карелин

Преподаватель А. Ю. Скрябнев

Санкт-Петербург

2021

1. Задание

1. В соответствии с номером варианта задания аппроксимировать таблично

заданные значения неизвестной функции методом наименьших квадратов

полиномами 1, 2, 3 и 4 степеней. При этом:

• 
  Для полиномов 1, 2, 3 и 4 степеней найти их коэффициенты путем решения систем линейных уравнений.
  
• 
  Для полиномов 1 и 2 степени также найти коэффициенты с помощью функции regress.
  
• 
  Для полинома 3-й степени также найти коэффициенты с помощью функции linfit.
  
• 
  Для полинома 4-й степени также найти коэффициенты с помощью функции interp.
  

2. Построить совмещенный график заданных узлов и всех полиномов.

3. Построить график суммы квадратов отклонений полиномов во всех узлах

в зависимости от степени полинома

2. Цель работы

Целью работы является получение навыков аппроксимации дискретных данных полиномом и исследование погрешностей аппроксимации в зависимости от степени полинома.

3. Краткие теоретические сведенья.

Метод наименьших квадратов применяют, когда необходимо вывести формулу аппроксимирующей кривой, описывающей некоторую зависимость, полученную в результате, например, эксперимента. Поскольку экспериментальные данные получают, как правило, с некоторой погрешностью, то обычно находят аппроксимирующую кривую, не проходящую через экспериментальные точки. В то же время она учитывает исследуемую закономерность, сглаживая случайные выбросы результатов эксперимента. В качестве аппроксимирующей функции может использоваться линейная комбинация F(x) любых функций:



где 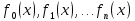набор любых функций, называемых базисными; – набор коэффициентов.

Довольно часто в качестве базисных функций используют комбинацию из степенной последовательности аргумента . При этом аппроксимирующая функция будет являться алгебраическим полиномом. Именно этот случай и рассматривается в работе.

Пусть некоторая функция задана таблицей значений y_i в узлах x_i (i=0,1, 2,…,m), где (m+1) – количество узлов, а m – число интервалов разбиения заданного промежутка.



Требуется определить коэффициенты полинома



Таким образом, чтобы сумма S квадратов отклонений полинома P(x) от значений y_i аппроксимируемой функции в заданных точках была бы минимальной, т.е.



Если степень полинома n=m, то искомый полином будет интерполяционным и пройдет через все узлы и отклонения будут нулевыми. Стремясь понизить степень полинома, принимают ni, y_i). Сумма квадратов отклонений зависит от коэффициентов полинома . Поскольку функция S принимает только положительные значения и имеет минимум, вычислим частные производные по всем переменным и приравняем их нулю:



Получаем систему уравнений



Выполнив суммирование, собрав коэффициенты при каждом и перенеся не содержащие их суммы в правую часть, получим СЛАУ относительно неизвестных



В матричной форме эту систему можно записать как aꞏC= b, где: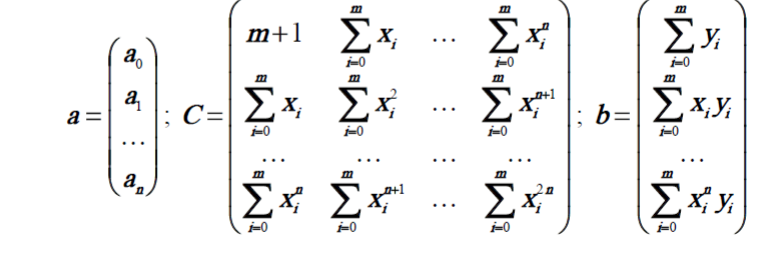



Решение этой системы позволяет найти все коэффициенты

4. 
   Выполненное задание
   

4.1)Задание узлов и их значений, а также составления матрицы и вектора.



4.2) Нахождения коэффициентов полиномов 1 – 4 степеней путем решения СЛАУ


4.3) Нахождения коэффициентов полиномов 1, 2 степени с помощью функции regress



4.4) Нахождения коэффициентов полинома 3 степени с помощью функции linfit



4.5) Нахождения коэффициентов полинома 4 степени с помощью функции interp



4.6) Построить совмещенный график заданных узлов и всех полиномов.



4.6) Построить график суммы квадратов отклонений полиномов во всех узлах в зависимости от степени полинома.

5. 
   Вывод.
   

В ходе выполнения лабораторной работы был освоен метод аппроксимации наименьшими квадратами. Из проделанных вычислений становится ясно, что чем выше степень полинома, тем точнее получается аппроксимации, но степень полинома, должна быть меньше степени функции, иначе полином будет интерполяционным и пройдет через все узлы и отклонения будут нулевыми.