Автоматизация анализа устойчивости САУ. Автоматизация анализа устойчивости сау
 Скачать 119.41 Kb. Скачать 119.41 Kb.
|
|
«Российский университет транспорта» (МИИТ) «Институт транспортной техники и систем управления» (ИТТСУ) Кафедра «Управление и защита информации» Практическая работа №4 по дисциплине: «Автоматизированное проектирование средств и систем управления» на тему: «Автоматизация анализа устойчивости САУ» Выполнил: Ст.гр. . Проверил: к.т.н, доцент . Москва – 2018 Одним из первых вопросов, возникающих при исследовании и проектировании линейных систем управления, является вопрос об их устойчивости. Линейная система называется устойчивой, если при выведении ее внешними воздействиями из состояния равновесия (покоя) она возвращается в него после прекращения внешних воздействий. Если после прекращения воздействия система не возвращается к состоянию равновесия, то она является не устойчивой. Для нормального функционирования системы управления необходимо, чтобы она была устойчивой, так как в противном случае в ней возникают большие ошибки. Определение устойчивости обычно приводят на начальном этапе создания системы управления. Это объясняется двумя причинами: Проведение анализа устойчивости не вызывает больших трудозатрат; Неустойчивые системы могут быть скорректированы, т.е. преобразованы в устойчивые с помощью добавления специальных корректирующих звеньев. Критерий устойчивости Рауса-Гурвица Один из способов анализа линейной стационарной динамической системы на устойчивость, разработанный немецким математиком Адольфом Гурвицом. Наряду с критерием Рауса является представителем семейства алгебраических критериев устойчивости, в отличие от частотных критериев, таких, как критерий устойчивости Найквиста — Михайлова. Достоинством метода является принципиальная простота, недостатком - необходимость выполнения операции вычисления определителя, которая связана с определенными вычислительными тонкостями (например, для больших матриц может появиться значительная вычислительная ошибка). Метод работает с коэффициентами характеристического уравнения системы. Пусть  передаточная функция системы характеристическое уравнение системы. Представим характеристический полином U(s) в виде Из коэффициентов характеристического уравнения строится определитель Гурвица по алгоритму: по главной диагонали слева направо выставляются все коэффициенты характеристического уравнения от a1 до an; от каждого элемента диагонали вверх и вниз достраиваются столбцы определителя так, чтобы индексы убывали сверху вниз; на место коэффициентов с индексами меньше нуля или больше n ставятся нули. Размерность матрицы Гурвица определяется максимальной степенью при s в характеристическом уравнении (т.е. n).  Тогда согласно критерию Гурвица: Для того, чтобы динамическая система была устойчива, необходимо и достаточно, чтобы все n главных диагональных миноров определителя Гурвица были положительны, при условии a0 > 0. Эти миноры называются определителями Гурвица. Критерий устойчивости Найквиста В 1932 году Найквист предложил принципиально новый критерий устойчивости. В отличие от критерия Гурвица, который устанавливает принадлежность корней к левой полуплоскости для любого полинома или алгебраического уравнения, критерий Найквиста предназначен для исследования устойчивости только замкнутых систем. Критерий Найквиста — это графоаналитический критерий. Характерной его особенностью является то, что вывод об устойчивости или неустойчивости замкнутой системы делается в зависимости от вида амплитудно-фазовой (а. ф. х.) или логарифмических частотных характеристик (л. ч. х.) разомкнутой системы. Помимо исследования устойчивости по виду указанных характеристик можно оценить и некоторые качественные показатели замкнутой системы, например, запас устойчивости. Более того, появляется возможность указать, как и за счет каких средств неустойчивая замкнутая система может быть сделана устойчивой и как можно повысить качество устойчивой замкнутой системы. Передаточная функция:  При подстановке p = jω получается частотная передаточная функция разомкнутой системы Частотная передаточная функция разомкнутой системы представляет собой комплексное число. Представим себе систему управления в разомкнутом состоянии в виде некоторого звена с передаточной функцией W(p). Если на вход этого звена подавать сигнал ошибки в виде гармонических колебаний х = Xmax sin ωt, с амплитудой Хmах и частотой ω, то в установившемся режиме на выходе управляемая величина будет изменяться также по гармоническому закону у = Ymax sin (ωt + ψ) с амплитудой Ymax, той же частотой и фазовым сдвигом ψ. Модуль частотной передаточной функции представляет собой отношение амплитуд выходной и входной величин:𝐴(𝜔) =𝑌𝑚𝑎𝑥/𝑋𝑚𝑎𝑥 а аргумент —сдвиг фаз ψ. При постоянном значении Хmах амплитуда Ymах зависит от частоты входного сигнала: Ymах = Ymах (ω). От частоты зависит и сдвиг фаз, или фаза: ψ = ψ(ω).  Если изменять частоту входного воздействия от 0 до ∞ и откладывать на комплексной плоскости точки, соответствующие получающимся комплексным числам, то геометрическое место этих точек образует амплитудно-фазовую характеристику разомкнутой системы . На амплитудно-фазовой характеристике для удобства могут отмечаться точки, соответствующие определенным частотам, например ω1 , ω2 , ω3 и т. д. Вдоль кривой иногда рисуют стрелки, которые показывают направление возрастания частоты ω. В реальных системах всегда удовлетворяется условие m < n. Поэтому при частоте, стремящейся к бесконечности, модуль частотной передаточной функции стремится к нулю и точка с частотой ω → ∞ попадает в начало координат. 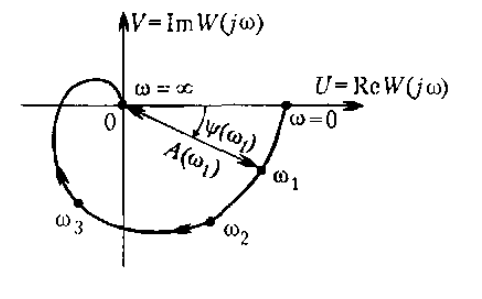 Это также частотный критерий, позволяющий судить об устойчивости системы, замкнутой единичной отрицательной обратной связью, по амплитудно-фазовой частотной характеристике разомкнутого контура. Предварительно требуется исследование устойчивости разомкнутой системы, как правило, по алгебраическим критериям. Для устойчивых и неустойчивых в разомкнутом состоянии систем формулировки критерия разные. Если система устойчива в разомкнутом состоянии, то для устойчивости в замкнутом состоянии необходимо и достаточно, чтобы амплитудно-фазовая частотная характеристика разомкнутого контура не охватывала точку с координатами (-1, j0). Для систем, неустойчивых в разомкнутых состояниях, критерий Найквиста имеет такую формулировку: если разомкнутая система неустойчива и имеет m корней в правой полуплоскости, то для устойчивости в замкнутом состоянии необходимо и достаточно, чтобы амплитудно-фазовая характеристика разомкнутого контура охватывала точку с координатами (-1, j0) m/2 раз. Если система имеет местные обратные связи, то необходимо проверить устойчивость внутренних контуров любым критерием. Пример: задана передаточная функция системы управления Исследовать её на устойчивость. Сделаем замену s = jω и найдём АФЧХ: 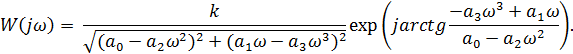 Кривая пересекает ось -1, если arctg φ = π . В этом случае - a3ω3 + a1ω = 0. Следовательно, ω2 = а1 /a3 . При а1 / а3 = 1 ω = 1 и А(1) = k /(а0 - а2). Система может быть устойчивой или неустойчивой в зависимости от соотношения величин k, а2 , а0. Замкнутая система устойчива, если A(Ω) < 1. Таким образом, условие устойчивости замкнутой системы. 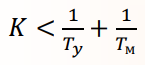 Критерий устойчивости Михайлова Описанные выше критерии устойчивости не работают, если передаточная функция системы имеет запаздывание, то есть может быть записана в виде 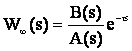 , ,где t - запаздывание. В этом случае характеристическое выражение замкнутой системы полиномом не является и его корни определить невозможно. Для определения устойчивости в данном случае используются частотные критерии Михайлова и Найквиста. Порядок применения критерия Михайлова: 1) Записывается характеристическое выражение замкнутой системы: Dз(s) = A(s) + B(s).e-ts. 2) Подставляется s = jw: Dз(jw) =Re(w) + Im(w). 3) Записывается уравнение годографа Михайлова Dз(jw) и строится кривая на комплексной плоскости. Для устойчивой АСР необходимо и достаточно, чтобы годограф Михайлова (см. рис.), начинаясь при w = 0 на положительной вещественной полуоси, обходил последовательно в положительном направлении (против часовой стрелки) при возрастании w от 0 до ¥ n квадрантов, где n - степень характеристического полинома. Если годограф Михайлова проходит через начало координат, то говорят, что система находится на границе устойчивости.  |
