Задачи по матлогике. Будет ли логичным следующее рассуждение Намеченная атака удастся, если захватить
 Скачать 199.23 Kb.
|
|
1.) Будет ли логичным следующее рассуждение: Намеченная атака удастся, если захватить противника врасплох или его позиции плохо защищены. Захватить противника врасплох можно только, если он беспечен. Он не будет беспечен, если его позиции плохо защищены. Следовательно, намеченная атака не удастся. Не будет Введем следующие обозначения: A – победа B – противник захвачен врасплох C – позиции плохо защищены A = B  C, если мы примем C = 1 и B = 0, то A = 1, следовательно, атака удастся и рассуждение не логично.2.) Провести исследование булевой функции f (x, y, z) ((z y) x)((xy) (z x)) : А.) Построим таблицу функции
Б.) Построим СДНФ этой функции 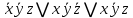 Упростим полученное выражение с помощью метода минимизирующих карт,
Минимизированная ДНФ 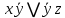 Построим многочлен Жегалкина 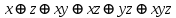 Построим таблицу двойственной функции
Построим СКНФ двойственной функции  Проверим исходную функцию на принадлежность основным классам замкнутости
3.) Привести формулу логики предикатов сначала в ПНФ, затем в СНФ: F = x(yP(y, α) ↔ Q(x)) ПНФ: F = x(yP(y, α) ↔ Q(x)) = x((yP(y, α) → Q(x))&(Q(x) → yP(y, α))); F = x((yP(y, α) → Q(x))&(Q(x) → yP(y, α))) = x((yP(y, α) Q(x))&(Q(x) yP(y, α))) = x((yP(y, α) Q(x))&(Q(x) yP(y, α))); F = x((yP(y, α) Q(x))&(Q(x) yP(y, α))) = x((yP(y, α) Q(x))&(Q(x) yP(y, α))) = x((yP(y, α) Q(x)) (Q(x) yP(y, α))) = x(yP(y, α)&Q(x) Q(x)&yP(y, α)) = x(yP(y, α)&Q(x) Q(x)&yP(y, α)) = x(yP(y, α)&Q(x) Q(x)&yP(y, α)); F = x(yP(y, α)&Q(x) Q(x)&yP(y, α)) = x(wP(w, α)&Q(x) Q(x)&yP(y, α)); F = x(wP(w, α)&Q(x) Q(x)&yP(y, α)) =xwy(P(w, α)&Q(x) Q(x)&P(y, α)); КНФ: F = xwy(P(w, α)&Q(x) Q(x)&P(y, α)) = xwy((P(w, α) Q(x)&P(y, α))&(Q(x) Q(x)&P(y, α))) = xwy((P(w, α) Q(x))&(P(w, α) P(y, α))&(Q(x) P(y, α))) 2. Приведем ПНФ формулы к СНФ F = xwy((P(w, α) Q(x))&(P(w, α) P(y, α))&(Q(x) P(y, α))) = = xw((P(w, α) Q(x))&(P(w, α) P(f(x, w), α))&(Q(x) P(f(x, w), α))) – СНФ. 4.) Машина Тьюринга имеет алфавит из трех символов2,1,* (символ означает отсутствие символа на ленте), два состоянияq0 ,q2 , из которых q0 – начальное состояние, q2 – конечное. Символ R означает сдвиг читающей головки вправо по ленте, L – влево, E – головка остается на месте. В начальный момент головка указывает на крайний левый символ записи. Команды машины задаются набором: q0 2 q01R, q01 q0 2L, q0* q2 2E. Какой результат даст машина на наборе22122?  Ответ: 222222 5.) Пусть A , . Построить алгоритм Маркова, который приписывает символ к концу слова. Припишем * слева к слову P, затем перегоним его через все буквы слова    6. Построить конечный автомат, распознающий язык L над алфавитом {a, b}, длина слов которого кратна трем.    a, b a, b a, b q3 q2 q1 q0    7. Описать конечный автомат, распознающий язык, заданный регулярным выражением: (а + b + cd*)* Строим граф для выражения a + b  a q4 q3   ϵ ϵ q2  q8  ϵ ϵ b q7 q6  ϵ Строим граф для выражения cd*  c   ϵ q12 d q11 q10 ϵ q9    ϵ Соединяем построенные автоматы ϵ  a q4 q3    ϵ ϵ q8    ϵ b ϵ ϵ q2  ϵ ϵ q7 q6   ϵ ϵ q13 q14 q1 q0       ϵ ϵ c   ϵ q12 d q10 q11 q9   ϵ ϵ 8. Построить порождающую грамматику для языка L = {(ac)n (cb)n, n > 0}. Зададим КС-грамматику для этого языка. S → aсSсb и S → aссb. Пример aсaсaссbсbсb: S → aсSсb → aсaсSсbсb → aсaсaссbсbсb. 9. Описать язык, который определяет КС грамматика S::= 0|S0S. Удовлетворяет ли она условию однозначности ветвления по первому символу. <буква>::= <цифра>|(<буква><цифра><буква>). <буква>::= S, <цифра>::= 0. Грамматика удовлетворяет условию однозначности ветвления по первому символу, так как L(<буква>) ≠ L(<цифра>), то есть L(<буква>) ∩ L(<цифра>) = . 10. Для грамматики, заданной следующими правилами вывода, построить эквивалентный ей конечный автомат: S → bS|aA|a|b, A → aA|bS|a 1) Sb → S 2) Sa → A 3) Sa → F 4) Sb → F 5) Аa →А 6) Аb →S 7) Аa →F a a b     b A S   a b  a F 11.) Дана инфиксная скобочная форма записи арифметического выражения: a b*c d e f Перевести ее в постфиксную форму. abc*+def--/ |
1
1