информатика. Курсовая. Численное интегрирование методом левых прямоугольников
 Скачать 189.79 Kb. Скачать 189.79 Kb.
|
|
НИЖЕГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ им. Р.Е. Алексеева ИТС Кафедра: «Высшая математика» Курсовая работа по информатике Тема: «Численное интегрирование методом левых прямоугольников» Вариант № 6 Выполнил: студент группы 19-ЭТКз-1 ФИО Проверила: Шувалова Т.Е. Нижний Новгород 2022 Оглавление Введение 3 1.Постановка задачи численного интегрирования 4 2.Метод левых прямоугольников 8 3.Блок-схема метода левых прямоугольников вычисления интеграла 10 4.Контрольный пример 11 5.Программа на языке Pascal и результаты вычисления интеграла 12 6.Вычисления интеграла и графики в программе MathСad 13 7.Вычисления интеграла и графики в EXCEL 14 Вывод 16 Список литературы 17 ВведениеЧисленные методы (вычислительные методы, методы вычислений) — раздел вычислительной математики, изучающий приближенные способы решения типовых математических задач, которые либо не решаются, либо трудно решаются точными аналитическими методами (вычислительная математика в узком смысле). Примерами типовых задач являются численное решение уравнений, численные дифференцирование и интегрирование и др. Численное интегрирование (или квадратура) — представляет собой вычисление значения определённого интеграла (как правило, приближённое). Под численным интегрированием понимают набор численных методов для нахождения значения определённого интеграла. Численное интегрирование применяется, когда: Сама подынтегральная функция не задана аналитически. Например, она представлена в виде таблицы значений в узлах некоторой расчётной сетки. Аналитическое представление подынтегральной функции известно, но её первообразная не выражается через аналитические функции. В этих двух случаях невозможно вычисление интеграла по формуле Ньютона — Лейбница. Также возможна ситуация, когда вид первообразной настолько сложен, что быстрее вычислить значение интеграла численным методом. Точное нахождение первообразной (или интеграла) произвольных функций — процедура более сложная, чем дифференцирование, то есть нахождение производной. Зачастую выразить интеграл в элементарных функциях невозможно. Основная идея большинства методов численного интегрирования состоит в замене подынтегральной функции на более простую, интеграл от которой легко вычисляется аналитически. Постановка задачи численного интегрированияПусть требуется вычислить интеграл 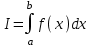 (1) (1)Из курса математического анализа известно, что для непрерывной на отрезке [a,b] функции f интеграл (19) существует и равен разности значений для первообразной F для функции fв точках b и a: 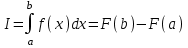 . (2) . (2)Однако в подавляющем большинстве практических задач первообразную Fне удается выразить через элементарные функции. Кроме того, функция f часто задается в виде таблицы ее значений для определенных значений аргумента. Все это порождает потребность в приближенных методах вычислении интеграла (1), которые можно условно подразделить на аналитические и численные. Первые заключаются в приближенном построении первообразной и дальнейшем использовании формулы (2). Вторые позволяют непосредственно найти числовое значение интеграла, основываясь на известных значениях подынтегральной функции (а иногда и ее производной) в заданных точках, называемых узлами. В настоящей главе остановимся лишь на численных методах интегрирования функций. Сам процесс численного определения интеграла называется квадратурой, а соответствующие формулы – квадратурными. Задача: На отрезке [a,b] в узлах 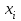 заданы значения заданы значения 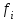 некоторой функции f, принадлежащей определенному классу F. Тре6уется приближенно вычислить интеграл (1). Так обычно ставится задача численного интегрирования в том случае, когда подынтегральная функция задана в виде таблицы. некоторой функции f, принадлежащей определенному классу F. Тре6уется приближенно вычислить интеграл (1). Так обычно ставится задача численного интегрирования в том случае, когда подынтегральная функция задана в виде таблицы.Один из способов решения сформулированной задачи основан на использовании различных квадратурных формул вида 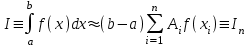 (3) (3)С известным остаточным членом 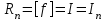 или его оценкой. или его оценкой.В общем случае, как узловые точки 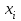 , так и весовые множители (веса) , так и весовые множители (веса) 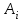 заранее не известны и подлежат определению при выводе каждой конкретной квадратурной формулы на основе предъявляемых к ней требований. заранее не известны и подлежат определению при выводе каждой конкретной квадратурной формулы на основе предъявляемых к ней требований.Алгоритм решения задачи: 1) Выбирают конкретную квадратурную формулу (3) и вычисляют 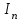 . Если значения функции . Если значения функции 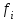 заданы приближенно, то фактически вычисляют лишь приближенное значение заданы приближенно, то фактически вычисляют лишь приближенное значение 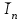 для точного для точного 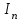 . .2) Приближенно принимают, что 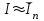 3) Пользуясь конкретным выражением для остаточного члена или оценкой его для выбранной квадратурной формулы, вычисляют погрешность метода: 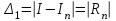 . .4) Определяют погрешность вычисления 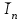 : :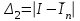 по погрешности приближения значений 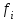 . .5) Находят полную абсолютную погрешность приближенного значения 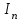 : :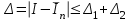 . .6) Получают решение задачи в виде 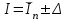 . .Используемые в алгоритме квадратурные формулы строятся на основании тех или иных критериев, определяющих положение узловых точек и величины весовых множителей. Такими критериями могут быть: представление интеграла в виде интегральной суммы; аппроксимация подынтегральной функции (например, многочленом) и последующее интегрирование аппроксимирующей функции; требование, чтобы формула (3) была абсолютно точной для определенного класса функций, и др. Метод левых прямоугольниковКак известно, определенный интеграл в силу своего построения есть предел интегральных сумм: 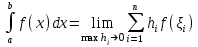 , (4) , (4)каждая, из которых соответствует некоторому разбиению 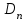 : : 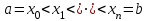 отрезка отрезка 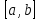 и произвольному набору точек и произвольному набору точек 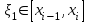 для каждого разбиения; для каждого разбиения; 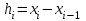 . .Ограничиваясь конечным числом слагаемых в правой части равенства (4) и принимая в качестве набора 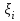 те или иные значения аргумента из отрезков те или иные значения аргумента из отрезков 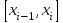 , можно получить различные формы приближенного интегрирования. Так, принимая в качестве набора , можно получить различные формы приближенного интегрирования. Так, принимая в качестве набора 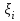 значения левых или правых концов отрезков значения левых или правых концов отрезков 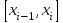 , получим соответственно формулу левых или правых прямоугольников , получим соответственно формулу левых или правых прямоугольников 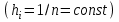 : :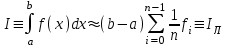 , (5) , (5)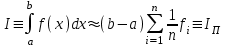 . (6) . (6)Наиболее часто используемой формулой, основанной на идее представления определенного интеграла в виде интегральной суммы, является формула прямоугольников, где в качестве 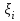 берут середины отрезков берут середины отрезков 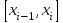 . Для равномерной сетки . Для равномерной сетки 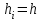 эта формула имеет следующий вид: эта формула имеет следующий вид: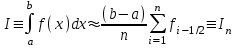 , (7) , (7)где 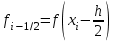 ; ;  ; ;  . .Выражение для остаточного члена квадратурной формулы (7): 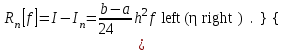 (8) (8)Таким образом, оценку погрешности квадратурной формулы (7) можно представить в следующем виде: 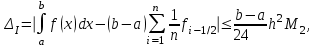 (9) (9)где 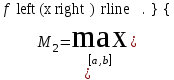 Суммарная вычислительная погрешность 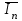 составит составит 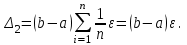 (10) (10)Эта погрешность не зависит от числа разбиений отрезка интегрирования, а пропорциональна только его длине. Блок-схема метода левых прямоугольников вычисления интеграла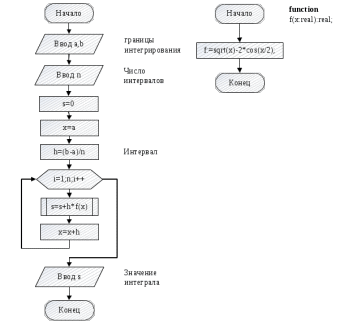 Рис. 1 Блок-схема вычисления интеграла методом левых прямоугольников Контрольный примерТребуется вычислить значение определенного интеграла 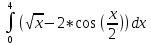 методом левых прямоугольников при n= 4; 8; 16. Пусть n = 4 h = (b-a)/n = 1 Формула левых прямоугольников (первая формула прямоугольников): f(x) = x^0,5-2*cos(x/2) f(0) = -2 f(1) = 1^0,5-2*cos(1/2) = -0,7552 f(2) = 2^0,5-2*cos(1) = 0,3336 f(3) = 3^0,5-2*cos(1,5) = 1,5906 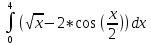 = 1*(-2-0,7552+0,3336+1,5906) = -0,83098 = 1*(-2-0,7552+0,3336+1,5906) = -0,83098Аналогичные расчеты для n = 8, 16. Аналитическое вычисление интеграла Представим исходный интеграл, как сумму интегралов: а) Это табличный интеграл: б) Это табличный интеграл: Вычислим определенный интеграл: F(0) = 0 = 1,696 Программа на языке Pascal и результаты вычисления интегралаКод программы Program Integral; Uses Crt; var a,b,s,x,h,s1,d,e:real; n,i: integer; function f(x:real):real; begin f:=sqrt(x)-2*cos(x/2); end; Begin clrscr; writeln('вычисление определенного интеграла'); writeln('методом левых прямоугольников'); a:=0; //нижняя граница b:=4; //верхняя граница write('Число интервало = '); readln(n); s:=0; x:=a; h:=(b-a)/n; for i:=1 to n do begin s:=s+h*f(x); x:=x+h; end; writeln('интеграл равен ', s:10:7); readln; end. 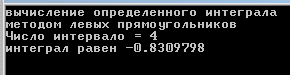 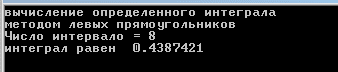 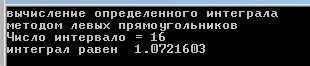 Вычисления интеграла и графики в программе MathСad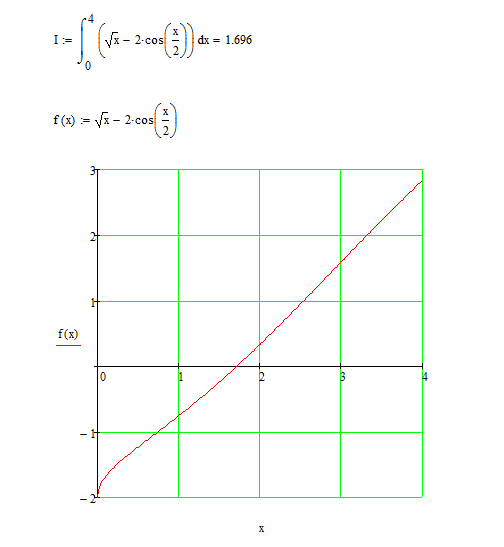 Рис. 2 Расчеты в MathCad Вычисления интеграла и графики в EXCELРасчеты в Excel 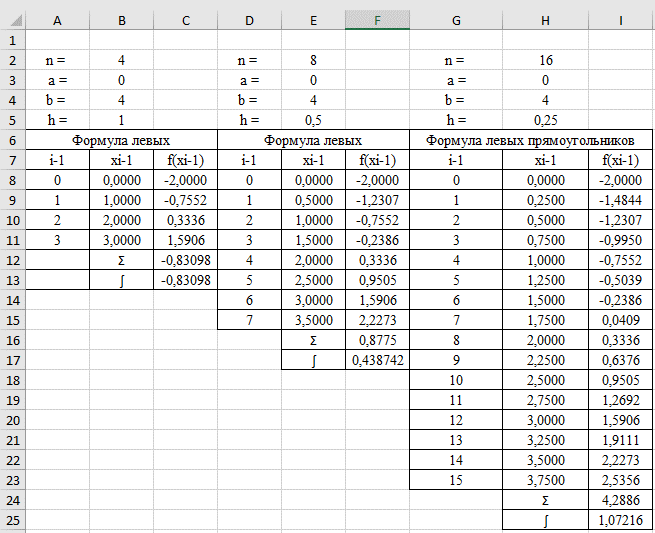 Рис. 3 Расчеты в Excel  Рис. 4 График подинтегральной функции ВыводВ работе рассмотрен метод левых прямоугольников для вычисления заданного определенного интеграла. Аналитическим способом получено точное значение интеграла = 1,696. Вычисление в пакете MathCad дает такое же значение. Расчеты сделанные с помощью программы, написанной на языке программирования Pascal, а также в Excel при заданном числе интервалов n = 4,8,16 дают очень большую погрешность. Это связано с тем, что недостатком метода левых прямоугольников является его сравнительно невысокая точность. Для повышения точности необходимо увеличивать значение n до 1...10 тысяч. Можно слегка модифицировать нашу программу, чтобы добиться нужной точности, допустим 0,001. Для этого будем наращивать n до тех пор, пока, разница значений интеграла на текущем и предыдущем шаге не станет меньше 0,001. 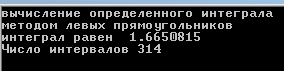 А если взять 0.000001, то 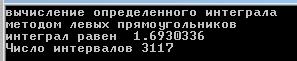 Как видим, для того, чтобы получить значение интеграла, которое бы отличалось от точного в третьем знаке, нам понадобилось разбить отрезок интегрирования на 3117 частей. Список литературы1. Заварыкин В.М., Житомирский В.Г., Лапчик М.П. Численные методы. М.: Просвещение, 1990. 2. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. М.: Наука, 1987. 3. Амосов А.А., Дубинский Ю.А., Копченова Н.В. Вычислительные методы для инженеров. М.:Высш. шк., 1994. 4. Волков Е.А. Численные методы. М.: Наука,1982. 5. КалиткинН.Н.Численные методы. М.: Наука,1978. 6. Шуп Т. Решение инженерных задач на ЭВМ. М.: Мир,1982. 7. Васильков Ю.В., Василькова Н.Н. Компьютерные технологии вычислений в математическом моделировании. М.: Финансы и статистика, 1999. 8. Абрамов, В. Г. Введение в язык паскаль / В.Г. Абрамов, Н.П. Трифонов, Г.Н. Трифонова. - М.: Наука, 2013. - 320 c. 9. Андреева, Т. А. Программирование на языке Pascal / Т.А. Андреева. - М.: Интернет-университет информационных технологий, Бином. Лаборатория знаний, 2013. - 240 c. |
