Конспект по математике на тему _Виды чисел. Действия с числами_.. Действия с рациональными и действительными числами

• Название: Действия с рациональными и действительными числами
• Дата: 04.04.2023
• Размер: 54.49 Kb.
• Имя файла: Конспект по математике на тему _Виды чисел. Действия с числами_..docx
• Тип: Документы; #1037525

Действия с рациональными и действительными числами

Действия с обыкновенными дробями

Вспомним определение:

Обыкновенная дробь – это число вида 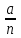, где а и n – натуральные числа.

Или:

Обыкновенная дробь – это число, состоящее из одной или нескольких частей (долей) единицы.

На примерах вспомним основные действия с дробями:

1)

Это смешанные числа с различными знаменателями. Чтобы их сложить, сначала необходимо привести дроби к неправильным:



Затем, выясняем, что наименьшим общим знаменателем (НОЗ), будет число 21 (если вы затрудняетесь найти НОЗ, достаточно заданные знаменатели перемножить). Тогда, первую дробь умножаем на 3, чтобы получить 21, а вторую на 7:



После этого, можно записать дроби на одной дробной черте и сложить числители:



В ответе дробь можно оставить в таком виде, целое не извлекать.

2)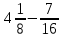

При вычитании выполняем аналогичные действия:



В данном случае, наименьшее общее число, на которое делились бы оба знаменателя -16. Поэтому, необходимо умножить на 2 только первую дробь:



3)

При умножении нужно перемножить числители и знаменатели обеих дробей:



Если есть такая возможность, то перед умножением нужно числа, стоящие в числителе и знаменателе, неважно, в каком порядке, сократить, разделив на одно и то же число: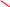



4)

При делении, дроби можно умножить, перевернув вторую дробь. Иногда этот метод называют умножением «крест – накрест» или просто «крестом»:

,

Замечаем, что числа 12 и 18 можно разделить на 6 (сократить), а 35 и 25 – на 5:



5)

Умножать смешанные числа нельзя, сначала их надо привести к неправильным дробям, а затем выполнять умножение:



6)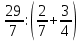

По правилам, сначала выполняется сложение в скобках, затем – деление. Можно эти действия объединить в одной записи: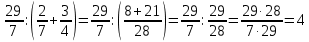



7)

В этом примере сначала выполняется деление, затем сложение. Обращаю ваше внимание, что при делении положительного числа на отрицательное, получится отрицательный знак:



В этом примере не было необходимости приводить смешанное число к неправильной дроби.

8)

Выполним действия в знаменателе:



Разделим числитель исходной дроби на найденный знаменатель:



Обратите внимание: если 1 умножать на обыкновенную дробь, то результатом будет сама дробь без изменений.

Если 1 делить на обыкновенную дробь, то она просто переворачивается.

Действия с конечными десятичными дробями

Конечная десятичная дробь - это любая дробь, которую можно представить в виде: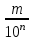

, где m - целое число, а n – натуральное.

Для записи ее используют десятичную запись, когда целая часть отделяется от дробной с помощью запятой.

Например: ; ; ; ;

Количество нулей равно количеству чисел после запятой

число 3,27 можно записать: ; число - 2,3 можно записать: .

В виде конечной десятичной дроби можно представить и некоторые обыкновенные дроби не имеющие знаменатель 10, 100, 1000…

Например, .

Чтобы получить знаменатель 100, надо числитель и знаменатель этой дроби умножить на 25:

;

;

Но не все обыкновенные дроби можно привести к конечным десятичным, например дроби со знаменателями 3, 5, 6, 7,… Эти числа, и многие другие, ни при каком умножении не привести к знаменателю , это бесконечные периодические дроби, о которых мы будем говорить позже.

Основные правила действий с конечными десятичными дробями

Чтобы выполнить сложение и вычитание десятичных дробей, их записывают одну под другой так, чтобы одинаковые разряды были друг под другом, а запятая под запятой, и сложить или вычесть числа так, как слагают или вычитают натуральные числа:

1,234 13,10

+ 3,317 - 0,37

4,551 12,73

Чтобы умножить десятичную дробь на натуральное число, надо:

1) умножить ее на это число, не обращая внимания на запятую;

2) в полученном произведении отделить столько цифр справа, сколько их отделено запятой в десятичной дроби.

Чтобы умножить десятичную дробь на 10, 100, 1000 и т.д., надо в этой дроби перенести запятую вправо на одну, две, три и т.д. цифры. Например: 12,733 ∙ 10 = 127,33.

Чтобы разделить десятичную дробь на натуральное число, надо:

1) разделить дробь на это число, не обращая внимания на запятую;

2) поставить в частном запятую, когда кончится деление целой части.

Чтобы разделить десятичную дробь на 10, 100, 1000,…, надо перенести запятую в этой дроби на столько цифр влево, сколько нулей стоит после единицы в делителе.

Например: 0,358 : 10 = 0,0358; 12,733 : 10 = 1,2733.

Чтобы умножить число на 0,1; 0,01; 0,001 (это то же самое, что разделить его на 10, 100, 1000), надо перенести запятую влево на столько цифр, сколько нулей стоит перед единицей в множителе.

Например: 12,733 ∙ 0,1 = 1,2733

Чтобы разделить десятичную дробь на 0,1; 0,01; 0,001, надо перенести запятую вправо на столько цифр, сколько в делителе стоит нулей перед единицей, т.е. умножить ее на 10, 100, 1000.

Например: 2,467 : 0,01 = 2,467 ∙ 100 = 246,7;

12,733 : 0,1 = 127,33.

Примеры.

1)

Разность в скобках можно найти устно, выполнив соответственно вычитание целых и дробных частей:



Умножение можно выполнить несколькими способами:

- можно выполнить столбиком умножение заданных чисел;

-можно выполнить умножение столбиком целых чисел и в ответе отделить запятой две последние цифры;

- можно привести эти числа к обыкновенным дробям и выполнить умножение:

2) 3,8 + 1,08 : 0,9

Сначала выполняем деление, легче это сделать в обыкновенных дробях, (но можно столбиком):



Теперь выполним сложение: 3,8 + 1,2 = 5

3)

Сначала выполним сложение в знаменателе:



Умножим числитель и знаменатель на 10 и выполним деление:



4)

Так как максимальное количество знаков после запятой в знаменателе и равно 4, умножим числитель и знаменатель (не каждое число), на 10000, чтобы привести числа к целым:



5)

Обратите внимание, при затруднении выполнения действий умножения или деления, целое число всегда можно представить, как дробь: .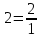
Смешанные примеры
Если в примере даны и конечные десятичные дроби и обыкновенные дроби, то их сначала нужно привести к одному виду: либо конечной десятичной либо к обыкновенной, для этого надо посмотреть на знаменатель обыкновенной дроби: можно ли его привести к 10, 100, 1000 и т.д. Если нет, то однозначно вычисления должны идти в обыкновенных дробях.

1)

В этом примере дробь не привести к конечной десятичной, поэтому приведем 0,99 к обыкновенной: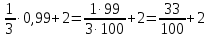



А теперь можно вернуться к конечной десятичной дроби: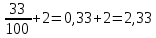



2)

3)

В этом примере обыкновенную дробь лучше привести к конечной десятичной, умножив ее числитель и знаменатель на 2: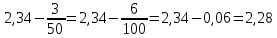



4)

Преобразование алгебраических выражений и дробей

Если дробь содержит алгебраическое выражение – выражение, содержащее буквенные неизвестные, то правила выполнения действий не меняются.

1)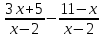

Эти дроби имеют одинаковый знаменатель, значит можно найти разность числителей. Но! Вычесть надо не число, а выражение, поэтому заключим его в скобки:



Раскроем скобки и приведем подобные:



В таком виде дробь сокращать нельзя! Поэтому, это – ответ.

2)

В этом выражении в знаменателе второй дроби неизвестные располагаются в другом порядке. Перепишем эту дробь, расположив неизвестные в нужном порядке: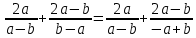



Теперь знаменатели не совпадают по знакам. Вынесем знак «-» за скобки в знаменателе второй дроби:



Этот минус изменит знак всей второй дроби (так как при делении положительного числа на отрицательное, имеем отрицательный результат):

.

3)

4)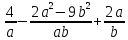

Заметим, что общим знаменателем всех трех дробей является произведение ab. Умножим первую дробь на b, а третью на a: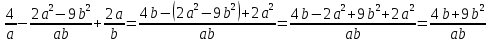



Сократить такую дробь можно только при вынесении общего множителя в числителе: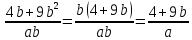



5)

Заметим, что при умножении знаменателей получается выражение:

– это выражение можно свернуть по формуле сокращенного умножения «разность квадратов»:



Приведем выражение в скобках к НОЗ и выполним все действия: