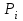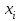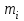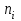ДГМ. Экзаменационный билет 307
 Скачать 0.52 Mb. Скачать 0.52 Mb.
|
|
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 307 1. В одном ящике 8 белых и 12 красных шаров, в другом ящике 10 белых, 5 черных и 5 красных шаров. Из первого переложили неизвестный шар во второй, а затем из второго достали два шара. а) В какую теоретическую схему “укладывается" эта задача? б) Записать соответствующую расчетную формулу и пояснить смысл входящих в нее величин. в) Какие значения для данного условия принимают величины, входящие в указанную выше формулу? г) Какова вероятность того, что оба шара красные. Решение. а) Если событие А может произойти только при выполнении одного из событий 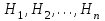 , которые образуют полную группу несовместных событий, то вероятность события А вычисляется по формуле полной вероятности. , которые образуют полную группу несовместных событий, то вероятность события А вычисляется по формуле полной вероятности.б) По условию из первого переложили неизвестный шар во второй, тогда возможны два случая: 1) переложили белый шар; 2) переложили красный шар. Применима формула полной вероятности 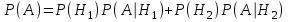 . .Событие А = «Из второго ящика достали два красных шара» ( из г)). Гипотезы: 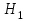 = «Во второй ящик переложили из первого белый шар». = «Во второй ящик переложили из первого белый шар».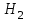 = «Во второй ящик переложили из первого красный шар». = «Во второй ящик переложили из первого красный шар».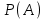 - вероятность события А, - вероятность события А, 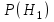 , , 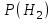 - вероятности гипотез, - вероятности гипотез, 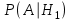 , , 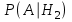 - условные вероятности события А, при условии что имели место гипотезы - условные вероятности события А, при условии что имели место гипотезы 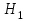 , , 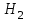 . .в) Всего в первом ящике имеется 8+12=20 шаров, тогда вычислим вероятности гипотез 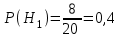 , , 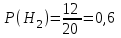 . .Вычислим условные вероятности события А. Если имела место гипотеза 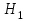 , то во втором ящике стало 10+1=11 белых, 5 черных и 5 красных шаров, всего 11+5+5=21, значит , то во втором ящике стало 10+1=11 белых, 5 черных и 5 красных шаров, всего 11+5+5=21, значит 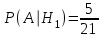 . .Если имела место гипотеза 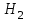 , то во втором ящике стало 10 белых, 5 черных и 5+1=6 красных шаров, всего 10+5+6=21, значит , то во втором ящике стало 10 белых, 5 черных и 5+1=6 красных шаров, всего 10+5+6=21, значит 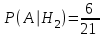 . .г) Вычислим 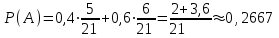 . .Ответ: а) формула полной вероятности, б) 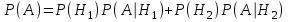 , ,в) 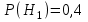 , , 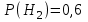 , , 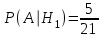 , , 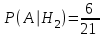 , ,г) 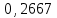 . .2. Вероятность рождения мальчика равна 0,51. Найти вероятность того, что а) среди 10 новорожденных 5 мальчиков, б) среди 100 новорожденных мальчиков от 45 до 55. в) среди 1000 от 450 до 550. г) Сравнить полученные результаты и прокомментировать. Решение. а) Имеем повторение испытаний. Вероятность появления события – рождение мальчика в каждом эксперименте постоянна и равна 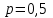 . Тогда имеем схему Бернулли (это биномиальное распределение). . Тогда имеем схему Бернулли (это биномиальное распределение).Формула Бернулли определяет вероятность появления ровно т раз события А в серии из 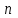 независимых испытаний, в каждом из которых вероятность появления события А равна р: независимых испытаний, в каждом из которых вероятность появления события А равна р: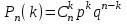 , где , где 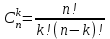 , , 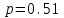 - вероятность рождения мальчика, - вероятность рождения мальчика, 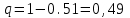 - вероятность рождения девочки. - вероятность рождения девочки.По условию 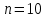 , , 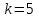 , тогда вычислим , тогда вычислим 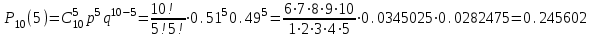 б) Найдем вероятность того, что при 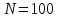 количество мальчиков составить от 45 до 55. количество мальчиков составить от 45 до 55.Количество испытаний 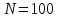 велико и применение формулы Бернулли в данном случае проблематично из-за сложных вычислений. велико и применение формулы Бернулли в данном случае проблематично из-за сложных вычислений.Вероятность того, что в 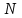 испытаниях событие наступит не менее испытаниях событие наступит не менее 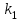 и не более и не более 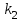 раз находится по формуле: раз находится по формуле: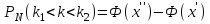 , где , где 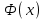 - функция Лапласа, ее значения определяются с помощью таблицы. - функция Лапласа, ее значения определяются с помощью таблицы. 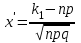 , , 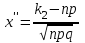 , тогда , тогда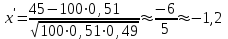 , , 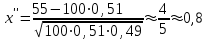 . . Учитывая, что функция Лапласа нечетная получим: 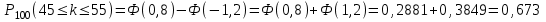 . .в) Найдем вероятность того, что при 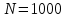 количество мальчиков составить от 450 до 550. количество мальчиков составить от 450 до 550.Количество испытаний 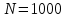 велико и применение формулы Бернулли в данном случае проблематично из-за сложных вычислений. велико и применение формулы Бернулли в данном случае проблематично из-за сложных вычислений.Вероятность того, что в 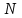 испытаниях событие наступит не менее испытаниях событие наступит не менее 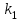 и не более и не более 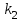 раз находится по формуле: раз находится по формуле: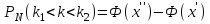 , где , где 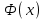 - функция Лапласа, ее значения определяются с помощью таблицы. - функция Лапласа, ее значения определяются с помощью таблицы. 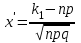 , , 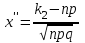 , тогда , тогда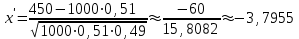 , , 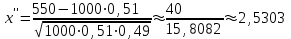 . . Учитывая, что функция Лапласа нечетная получим: 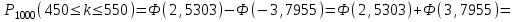 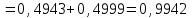 . .г) Если количество испытаний невелико, то следует применять теорему Бернулли, которая дает возможность точно рассчитать вероятность, если имеем большое количество испытаний, то следует применять приближенные формулы (локальная и интегральная теорема Лапласа и теорема Пуассона) в п. а) вычислена вероятность что родилось ровно 5 мальчиков, среди 10 новорожденных, в .п б) и в) приближенно вычислено, что количество мальчиков среди новорожденных составляет от 45 до 55 и от 450 до 550 соответственно от общего количества 100 и 1000. На основании в) можно утверждать, что при практически достоверно, что среди 1000 новорожденных количество мальчиков будет находиться в пределах от 450 до 550. Ответ: а) 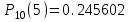 , , б) 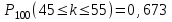 , ,в) 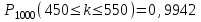 . .г) Если количество испытаний невелико, то следует применять теорему Бернулли, которая дает возможность точно рассчитать вероятность, если имеем большое количество испытаний, то следует применять приближенные формулы (локальная и интегральная теорема Лапласа и теорема Пуассона). На основании в) можно утверждать, что при практически достоверно, что среди 1000 новорожденных количество мальчиков будет находиться в пределах от 450 до 550. 3. СВ 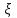 равномерно распределена на отрезке равномерно распределена на отрезке 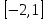 . Найти плотность вероятности СВ . Найти плотность вероятности СВ 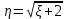 . Построить график функции . Построить график функции 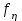 . . Решение. Запишем функцию плотности распределения для случайной величины 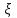 , равномерна распределенной на отрезке , равномерна распределенной на отрезке 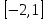 : : 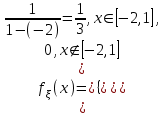 . .Функция 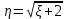 монотонна на отрезке монотонна на отрезке 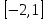 , она строго возрастает. , она строго возрастает.Применим формулу 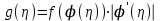 , где , где 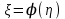 - обратная функция к - обратная функция к 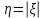 . .Из 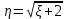 находим, что находим, что 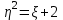 , значит , значит 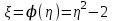 , тогда , тогда 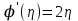 , откуда , откуда 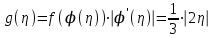 . .Определим, что при 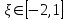 величина величина 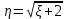 , , 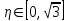 , тогда , тогда 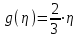 . .Обобщая полученные данные, найдем что 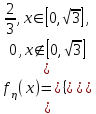 Построим график найденной функции. 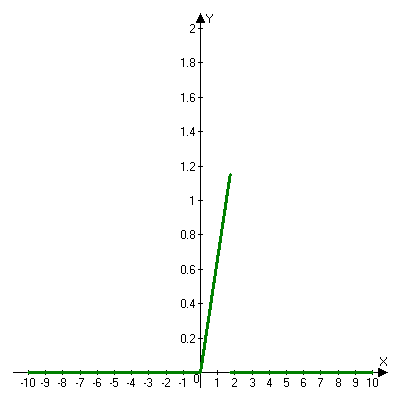 Рис.1. Ответ: 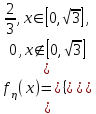 , рис.1. , рис.1.4. Задана двумерная СВ 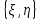 : :Таблица 1.
Найти а) безусловные законы распределения и центр, б) условный закон распределения 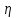 при при 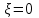 и, в) условное матожидание, и, в) условное матожидание,г) распределение 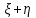 Решение. Заданное распределение не является совместным законом распределения СВ 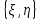 , поскольку сумма всех вероятностей равна , поскольку сумма всех вероятностей равна 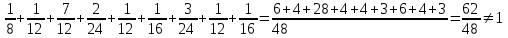 , заметим, что если вместо , заметим, что если вместо 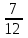 ( при ( при 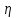 =-1 и =-1 и 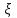 =1) положить =1) положить 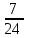 , то получим , то получим 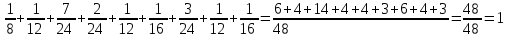 . .Все дальнейшие расчеты будем производить для совместного распределения (иначе не получим ряды распределения) при 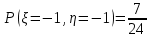 Таблица 2.
Для того, что бы найти безусловный закон распределения 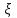 выполним сложение вероятностей по столбцам. выполним сложение вероятностей по столбцам.Таблица3.
Для того, что бы найти безусловный распределения 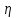 выполним сложение вероятностей по строкам. выполним сложение вероятностей по строкам.Таблица 4.
Вычислим математические ожидания 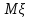 и и 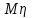 . .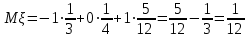 , ,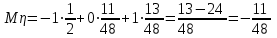 . .Центр распределения: 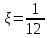 , , 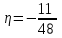 . .Б) найдем условный закон распределения 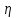 при при 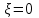 . .В таблице 3 найдено 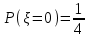 . .Условный закон распределения случайной величины 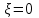 , найдем применяя формулу , найдем применяя формулу 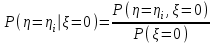 тогда тогда 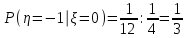 , , 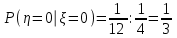 , , 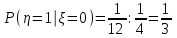 То есть Таблица 5.
В) Найдем условное математическое ожидание 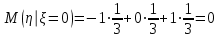 . .г) Найдем закон распределения СВ 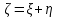 . .Вычислим все возможные суммы и запишем их вероятности 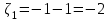 , , 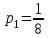 , , 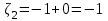 , , 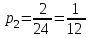 , , 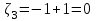 , , 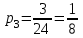 , ,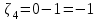 , , 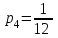 , , 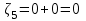 , , 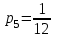 , ,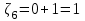 , , 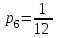 , , 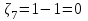 , , 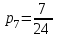 , , 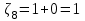 , , 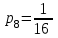 , , 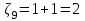 , , 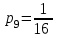 , , Объединим одинаковые значения и вычислим 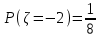 , , 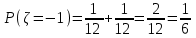 , , 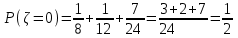 , , 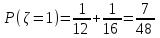 , , 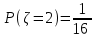 Таблица 6.
Ответ: заданное распределение не является законом распределения, рассматриваем распределение из таблицы 2. а) таблица3, таблица 4, центр 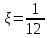 , , 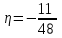 . .б) таблица 5, в) 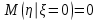 , г) таблица 6. , г) таблица 6.5. Задан статистический ряд Таблица 7.
а) Построить гистограмму. Найти 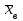 , моду, медиану и , моду, медиану и 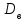 . .б) Оценить доверительный интервал для 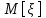 с надежностью с надежностью 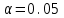 Решение. а) Построим гистограмму частот заданного ряда распределения, отметив на оси абсцисс – интервалы распределения, а на оси ординат их частоты и построим прямоугольники. 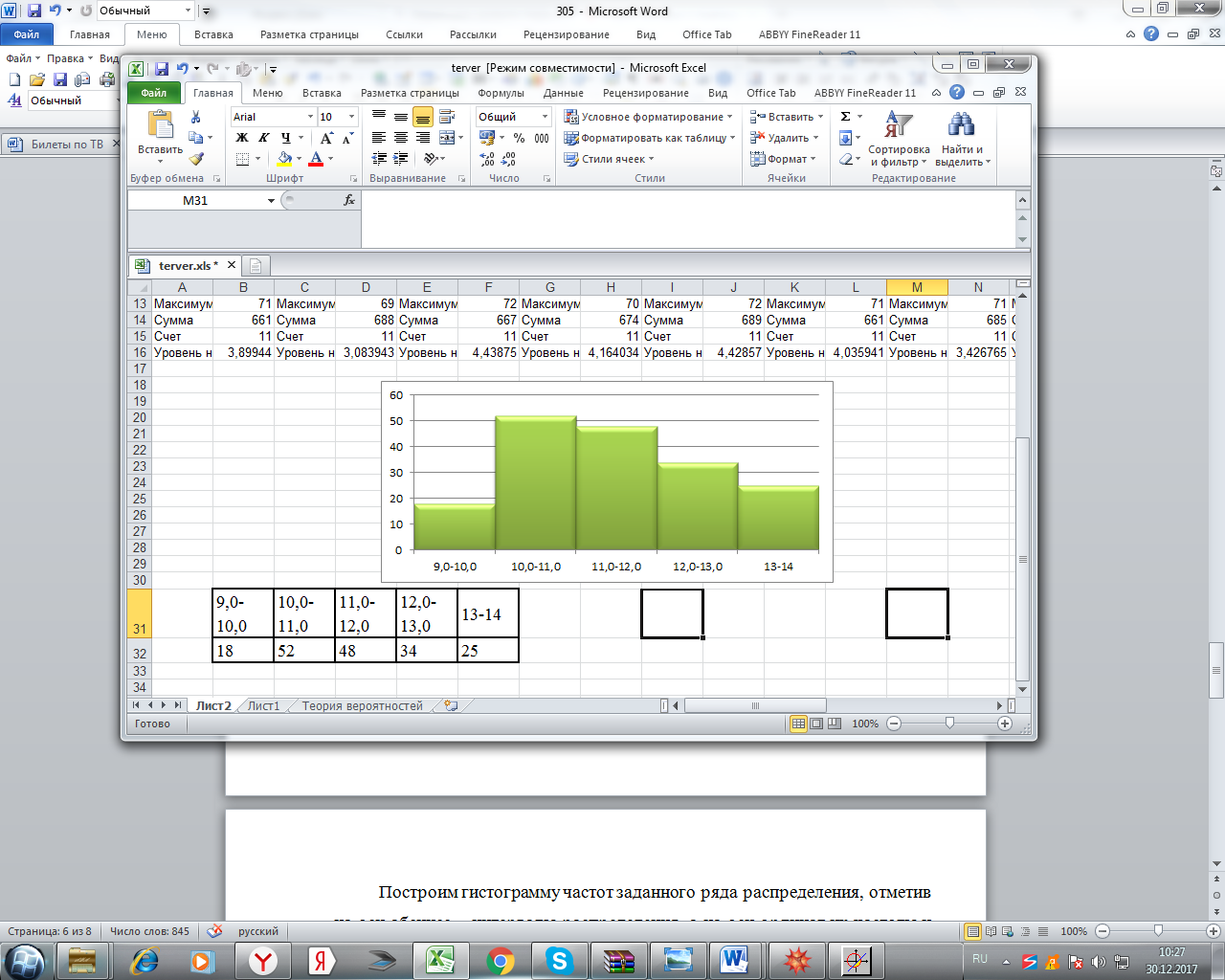 Рис.2. Для вычисления числовых характеристик перейдем от интервального ряда к вариационному, взяв в качестве вариант середины интервалов. Выборочный ряд распределения имеет вид. Таблица 8.
Объем выборки 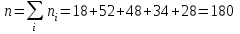 . .Выборочное среднее 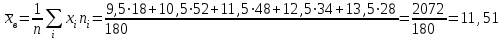 . .Выборочная дисперсия 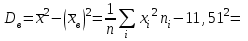 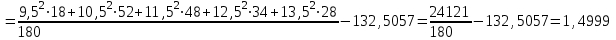 Для дискретного ряда вычислим моду и медиану Для дискретного ряда вычислим моду и медиану Мода – это значение, которое встречается в выборке наиболее часто, тогда мода 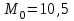 . .Медиана – это значение варианты, которое делит ранжированный ряд на две равные по численности совокупности (в нашем случае – это полусумма вариант, которые находятся на 89 и 90 месте) , 18+52=70, 70++48=118, тогда 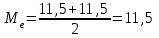 . .Для интервального ряда вычислим моду и медиану. В отличие от дискретных вариационных рядов определение моды и медианы по интервальным рядам требует проведения определенных расчетов на основе следующих формул: 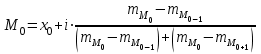 , , где 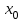 – нижняя граница модального интервала (модальным называется интервал, имеющий наибольшую частоту); – нижняя граница модального интервала (модальным называется интервал, имеющий наибольшую частоту); 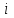 – величина модального интервала; – величина модального интервала; 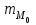 – частота модального интервала; – частота модального интервала; 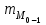 – частота интервала, предшествующего модальному; – частота интервала, предшествующего модальному; 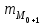 – частота интервала, следующего за модальным. – частота интервала, следующего за модальным. Тогда 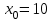 , , 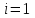 , , 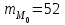 , , 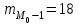 , , 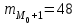 . .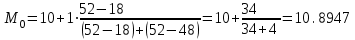 . .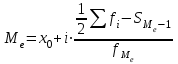 где 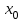 – нижняя граница медианного интервала (медианным называется первый интервал, накопленная частота которого превышает половину общей суммы частот); – нижняя граница медианного интервала (медианным называется первый интервал, накопленная частота которого превышает половину общей суммы частот); 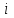 – величина медианного интервала; – величина медианного интервала; 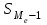 – накопленная частота интервала, предшествующего медианному; – накопленная частота интервала, предшествующего медианному; 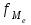 – частота медианного интервала. – частота медианного интервала. 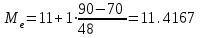 . .б) Доверительный интервал, покрывающий неизвестное математическое ожидание 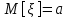 с вероятностью с вероятностью 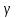 имеет вид: имеет вид: 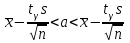 , где , где 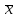 - среднее генеральной совокупности, - среднее генеральной совокупности, 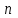 - объем выборки, - объем выборки, 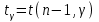 - для различных значений n и γ приведено в специальных таблицах, связанных с распределением Стьюдента, - для различных значений n и γ приведено в специальных таблицах, связанных с распределением Стьюдента, 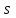 - исправленное среднеквадратическое отклонение. - исправленное среднеквадратическое отклонение.Для 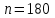 - объем выборки, и - объем выборки, и 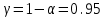 находим находим 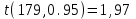 , вычислим , вычислим 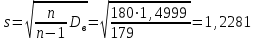 тогда 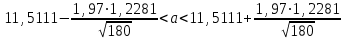 . .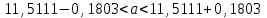 . .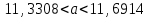 или или 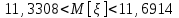 . .Ответ: рис.2., 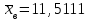 , , 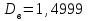 , для дискретного ряда , для дискретного ряда 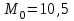 , , 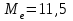 , для интервального ряда , для интервального ряда 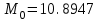 , , 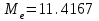 , , б) 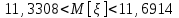 . . |