Метод конечных элементов. Физические основы метода. Физические основы метода
 Скачать 146.1 Kb. Скачать 146.1 Kb.
|
|
Физические основы метода МКЭ является универсальным методом решения задач механики сплошной среды, в том числе механики упругого твердого тела, а также расчета строительных, авиационных, ракетных, машиностроительных и других конструкций. Это обусловлено инвариантностью метода по отношению к геометрии конструкции, условиям ее закрепления и нагружения, а также высокой степенью приспособленности к автоматизации основных этапов расчета. Основная процедура МКЭ состоит в представлении перемещений конечных элементов через перемещения их узлов с помощью некоторых функций, называемых базисными функциями. Таким образом, полная потенциальная энергия 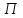 конечно-элементной модели конструкции является функцией ее узловых перемещений конечно-элементной модели конструкции является функцией ее узловых перемещений 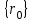 . . В состоянии равновесия конструкции 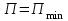 . Необходимое условие этого записывается в виде вариационного уравнения Лагранжа . Необходимое условие этого записывается в виде вариационного уравнения Лагранжа 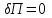 , что приводит к системе в итоге линейных алгебраических уравнений , что приводит к системе в итоге линейных алгебраических уравнений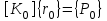 , , где 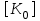 , , 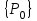 – соответственно матрица жесткости и вектор внешних узловых сил (вектор нагрузки) конечно-элементной модели конструкции. Смысл полученной системы уравнений состоит в равновесии внутренних и внешних узловых сил отмеченной модели. – соответственно матрица жесткости и вектор внешних узловых сил (вектор нагрузки) конечно-элементной модели конструкции. Смысл полученной системы уравнений состоит в равновесии внутренних и внешних узловых сил отмеченной модели.8.2. Матрица жесткости и вектор нагрузки конечного элемента Имеется некоторый конечный элемент (КЭ). Форма КЭ пока не конкретизируется. Представим перемещения 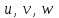 произвольной точки КЭ в виде произвольной точки КЭ в виде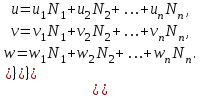 (8.1) (8.1) Здесь 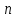 – число узлов; – число узлов; 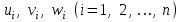 – перемещения узлов; – перемещения узлов; 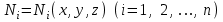 – базисные функции. – базисные функции.Введем вектор, содержащий узловые перемещения КЭ: 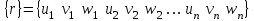 . . Имея данный вектор выражения (8.1) можно представить в виде 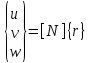 , , где 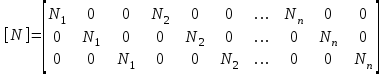 . . Подставляя данное представление в выражение (7.1) и принимая обозначения 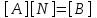 , , 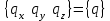 , получаем полную потенциальную энергию КЭ: , получаем полную потенциальную энергию КЭ: 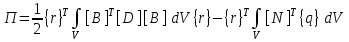 . . В состоянии равновесия КЭ 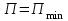 . Необходимое условие этого записывается в виде вариационного уравнения Лагранжа . Необходимое условие этого записывается в виде вариационного уравнения Лагранжа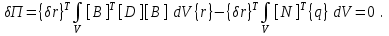 Отсюда с учетом условия 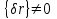 получаем систему уравнений получаем систему уравнений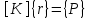 , , где 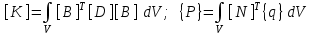 (8.2) (8.2)– соответственно матрица жесткости и вектор внешних узловых сил (вектор нагрузки) конечного элемента. С помощью формул (8.2) выражение для 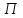 можно представить в виде можно представить в виде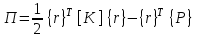 . . 8.3. Матрица жесткости и вектор нагрузки ферменного конечного элемента Ферменный КЭ (рис. 8.1) применяется для моделирования прямолинейных стержней, находящихся в одноосном однородном напряженном состоянии. Элемент имеет два узла. Считается, что площадь поперечного сечения 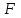 постоянна по длине элемента, а перемещение постоянна по длине элемента, а перемещение 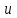 произвольной точки линейно зависит от его локальной координаты произвольной точки линейно зависит от его локальной координаты 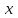 : : 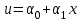 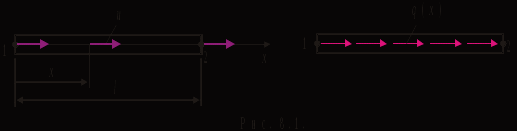 Постоянные 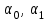 определяются из условий: определяются из условий: 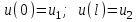 . Это дает систему уравнений 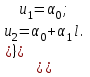 Отсюда следует: 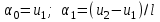 . Подставляя . Подставляя 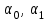 в исходное выражение для u, получаем в исходное выражение для u, получаем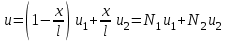 . (8.3) . (8.3) Здесь 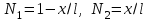 – базисные функции. – базисные функции.Выражение (8.3) можно записать в виде 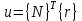 , , где 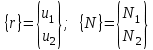 . . Для нахождения матрицы жесткости и вектора нагрузки ферменного КЭ воспользуемся общими формулами (8.2) полагая в них 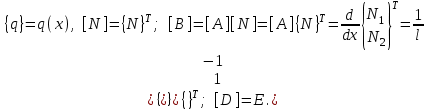 Таким образом, получаем 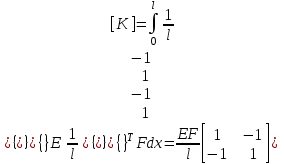 . . 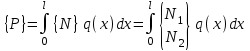 . . Будем считать, что нагрузка 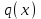 распределена в пределах элемента по линейному закону: распределена в пределах элемента по линейному закону: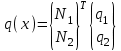 . . Подставляя этот результат в выражение для 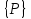 , получаем , получаем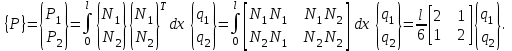 8.4. Матрица жесткости и вектор нагрузки балочного конечного элемента Балочный КЭ (рис. 8.2) применяется для моделирования поперечного изгиба стержней. Узловыми перемещениями элемента являются прогибы 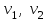 и углы поворота и углы поворота 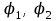 его узлов. На элемент действует погонная нагрузка его узлов. На элемент действует погонная нагрузка 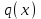 . .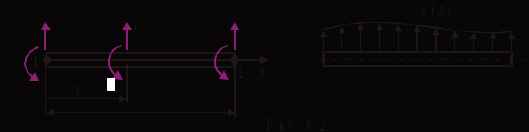 Представим прогиб 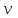 в пределах элемента в виде в пределах элемента в виде 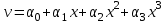 . . Постоянные 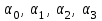 определяются из условий: определяются из условий: 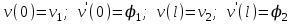 . . Это дает систему уравнений 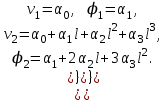 Отсюда следует: 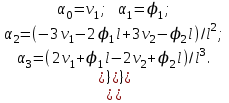 Подставляя это в выражение для 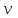 и собирая слагаемые, содержащие и собирая слагаемые, содержащие 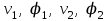 , получаем , получаем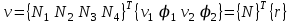 . . Здесь 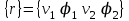 – вектор узловых перемещений КЭ; – вектор узловых перемещений КЭ; 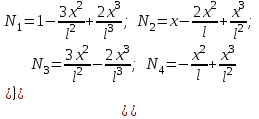 – базисные функции. Для получения матрицы жесткости элемента воспользуемся первой формулой в (8.2), полагая в ней 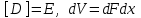 : :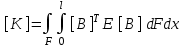 . (8.4) . (8.4)Матрица 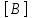 связывает деформацию связывает деформацию 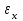 в произвольной точке M поперечного сечения элемента (рис. 8.3) с вектором узловых перемещений в произвольной точке M поперечного сечения элемента (рис. 8.3) с вектором узловых перемещений 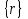 : :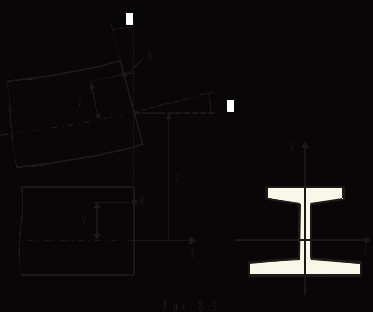 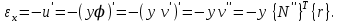 Отсюда следует: 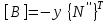 . С учетом этого выражение (8.4) принимает вид . С учетом этого выражение (8.4) принимает вид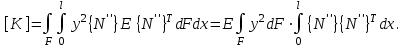 . (8.5) . (8.5)Интеграл по площади 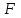 представляет момент инерции сечения относительно оси представляет момент инерции сечения относительно оси 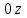 (рис. 8.3): (рис. 8.3): 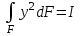 .Произведение .Произведение 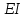 – жесткость элемента на изгиб. Выражение (8.5) с учетом этого получается таким: – жесткость элемента на изгиб. Выражение (8.5) с учетом этого получается таким: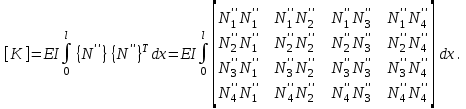 После нахождения интегралов получаем окончательное выражение для вычисления матрицы жесткости балочного КЭ: 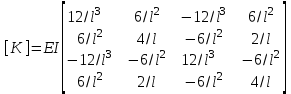 . . Вектор нагрузки вычисляется по второй формуле в (8.2) при 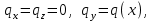 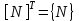 с заменой в ней с заменой в ней 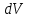 на на 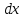 : : 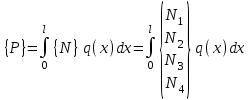 . . Для вычисления вектора 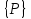 необходимо иметь зависимость необходимо иметь зависимость 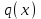 . Будем считать ее линейной: . Будем считать ее линейной: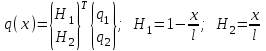 . . Это дает 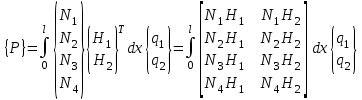 . . После нахождения определенных интегралов окончательно получаем 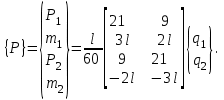 8.5. Матрица жесткости и вектор нагрузки рамного конечного элемента Рамный КЭ (рис. 8.4) применяется для моделирования стержней конструкции, работающих на растяжение-сжатие и изгиб. Вектор 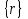 содержит продольные перемещения содержит продольные перемещения 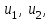 прогибы прогибы 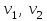 и углы поворота и углы поворота 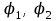 узлов элемента: узлов элемента: 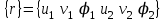 . .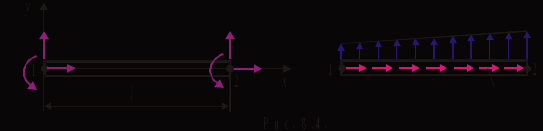 Из рис. 8.4 видно, что от перемещений 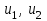 в элементе возникает только продольная сила в элементе возникает только продольная сила 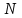 , а от , а от 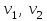 , , 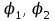 – только поперечная сила – только поперечная сила 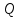 и изгибающий момент и изгибающий момент 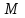 . Таким образом, состояния растяжения-сжатия и изгиба элемента являются независимыми. Это дает возможность сформировать матрицу жесткости . Таким образом, состояния растяжения-сжатия и изгиба элемента являются независимыми. Это дает возможность сформировать матрицу жесткости 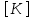 рамного КЭ из коэффициентов жесткости ферменного и балочного элементов: рамного КЭ из коэффициентов жесткости ферменного и балочного элементов: 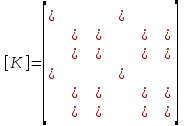 . . Символы 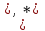 означают коэффициенты жесткости соответственно ферменного и балочного элементов. Аналогично формируется вектор нагрузки рамного КЭ: означают коэффициенты жесткости соответственно ферменного и балочного элементов. Аналогично формируется вектор нагрузки рамного КЭ: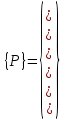 . . Символы 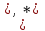 означают внешние узловые силы соответственно ферменного и балочного элементов. означают внешние узловые силы соответственно ферменного и балочного элементов. |
