курсовая. Союнов_Производная26.04.22. Физикоматематический факультет Кафедра математики и методики преподавания математики
 Скачать 0.67 Mb. Скачать 0.67 Mb.
|
|
Учреждение образования «Белорусский государственный педагогический университет имени Максима Танка» Физико-математический факультетКафедра математики и методики преподавания математикиПРИМЕНЕНИЕ ПРОИЗВОДНОЙ ПРИ РЕШЕНИИ ЗАДАЧ
Минск, 2022 ОГЛАВЛЕНИЕ ВВЕДЕНИЕ……………………………………………………………………….3 ГЛАВА 1. ПОНЯТИЯ НЕОБХОДИМЫЕ ДЛЯ РЕШЕНИЯ ЗАДАЧ С ПОМОЩЬЮ ПРОИЗВОДНОЙ………………………………………………….4 1.1. Исторические сведения………………………………………………4 1.2. Понятие производной, ее геометрический и физический смысл…..4 1.3. Понятие дифференциала функции…………………………………...6 ГЛАВА 2. ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ К РЕШЕНИЮ ЗАДАЧ……….8 2.1. Исследование функций и построение их графиков………………..8 2.2. Нахождение наибольшего и наименьшего значения функции, решение прикладных задач (задач на оптимум)……………………………….9 2.3. Определение периода функции……………………………………...10 2.4. Нахождение величины угла между прямыми и кривыми…………………………………………………………………………..11 2.5. Применение производной при решении задач в разных науках….12 2.5.1 Задачи по геометрии…………………………………………122.5.2 Задачи по физике……………………………………………..152.5.3. Решение экономических задач……………………………...17 2.6. Вычисление пределов функции с помощью правила Лопиталя…..18 2.7. Отбор кратных корней уравнения…………………………………..19 ЗАКЛЮЧЕНИЕ…………………………………………………………...21 СПИСОК ЛИТЕРАТУРЫ………………………………………………...22 ВВЕДЕНИЕ Рассматриваемая тема является одним из разделов курса алгебры и начала анализа. Она имеет широкое применение в таких науках как физика, геометрия и др. Математический аппарат этой темы помогает при вычислении определенных и неопределенных интегралов и пределов функций, при доказательстве неравенств, помогает в исследовании функций в высшей математике. Кроме того, данная тема имеет свою историю, ей занимались Термин «производная» является буквальным переводом на русский французкого слова derive, которое ввел в 1797 г. Ж. Лагранж (1736-1813); он же ввел современные обозначения  . Такое название отражает смысл понятия: функция . Такое название отражает смысл понятия: функция 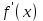 происходит из происходит из  , является производным от , является производным от  . И. Ньютон называл производную функцией флюксией, а саму функцию- флюентой. Г. Лейбниц говорил о дифференциальном отношении и обозначал производную как . И. Ньютон называл производную функцией флюксией, а саму функцию- флюентой. Г. Лейбниц говорил о дифференциальном отношении и обозначал производную как  . Символ . Символ  Лейбниц выбрал для обозначения дифференциала функции Лейбниц выбрал для обозначения дифференциала функции  . .Дифференциальное исчисление создано И. Ньютоном и Г. Лейбницем сравнительно недавно, в конце XVII столетия. Тем более поразительно, что за долго до этого Архимед не только решил задачу на построение касательной к такой сложной кривой, как спираль, но и сумел найти максимум функции  . В XVII в. на основе учения Г. Галилея о движении активно развивалась кинематическая концепция производной. . В XVII в. на основе учения Г. Галилея о движении активно развивалась кинематическая концепция производной.Эта тема интересна и мне. Цель моей работы – расширить свой кругозор и научиться решать задачи по данной теме. Чтобы достигнуть цели, мне пришлось решить следующие исследовательские задачи. 1. Подобрать и изучить материал по этой теме. 2. Из изученного материала выбрать главное. 3. Систематизировать основной материал в форме реферативно-поисковой работы. 4. Научиться решать задачи по теме. ГЛАВА 1. ПОНЯТИЯ НЕОБХОДИМЫЕ ДЛЯ РЕШЕНИЯ ЗАДАЧ С ПОМОЩЬЮ ПРОИЗВОДНОЙ 1.1 Исторические сведения Ряд задач дифференциального исчисления был решен еще в древности. Они встречались у Евклида. Ряд таких задач был решен Архимедом, разработавшим способ проведения касательной, примененный им к спирали, но применимый для других кривых. Основное понятие дифференциального исчисления – понятие производной – возникло в XVII в. В связи с необходимостью решения ряда задач из физики, механики и математики. Дифференциальное исчисление было создано Исаак Ньютоном и Готфрид Вильгельм Лейбницем на основе двух задач: 1) о разыскании касательной к произвольной линии2) о разыскании скорости при произвольном законе движения. Еще раньше понятие производной встречалось в работах итальянского математика Никколо Тартальи (около 1500 - 1557 гг.) - здесь появилась касательная в ходе изучения вопроса об угле наклона орудия, при котором обеспечивается наибольшая дальность полета снаряда. В 17 веке на основе учения Галилео Галилея о движении активно развивалась кинематическая концепция производной. Различные изложения стали встречаться в работах у Рене Декарта, французского математика Жиль де Роберваля, английского ученого Кинг Грегори. Большой вклад в изучение дифференциального исчисления внесли Гийом Франсуа Лопиталь, Даниил Бернулли, Жозеф Луи Лагранж, Леонард Эйлер, Иоганн Карл Фридрих Гаусс. [2] 1.2 Понятие производной, ее геометрический и физический смысл Понятие производной Пусть y = f(x) есть непрерывная функция аргумента x, определенная в промежутке (a; b), и пусть х0 - произвольная точка этого промежутка Дадим аргументу x приращение ∆x, тогда функция y = f(x) получит приращение ∆y = f(x + ∆x) - f(x). Предел, к которому стремится отношение ∆y / ∆x при ∆x → 0, называется производной от функции f(x). y'(x)= 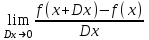 Геометрический смысл производной. Теперь дадим не менее важное геометрическое истолкование производной. Для этого нам, прежде всего, потребуется определение касательной к кривой в данной точке.  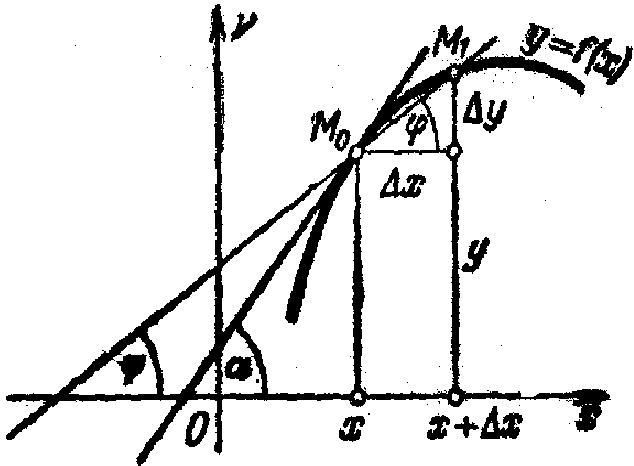 Рис. 1. Рис. 2. Пусть имеем кривую и на ней фиксированную точку 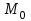 . Возьмем на кривой точку . Возьмем на кривой точку  и проведем секущую и проведем секущую (рис. 1). Если точка (рис. 1). Если точка  неограниченно приближается по кривой к точке неограниченно приближается по кривой к точке 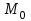 , то секущая , то секущая  занимает различные положения занимает различные положения 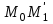 , ,  и т. д. и т. д.Если при неограниченном приближении точки  , по кривой к точке , по кривой к точке 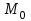 с любой стороны секущая стремится занять положение определенной прямой с любой стороны секущая стремится занять положение определенной прямой 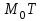 , то эта прямая называется касательной к кривой в точке , то эта прямая называется касательной к кривой в точке 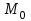 . .Определение 1. Прямая заданная уравнением  называется касательной к графику функции  в точке в точке 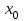 . . Рассмотрим функцию  и соответствующую этой функции кривую и соответствующую этой функции кривую . .В прямоугольной системе координат (рис. 2). При некотором значении 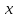 функция имеет значение функция имеет значение  . Этим значениям . Этим значениям 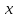 и и 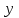 на кривой соответствует точка на кривой соответствует точка 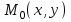 . Дадим аргументу . Дадим аргументу 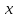 приращение приращение 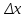 . Новому значению аргумента . Новому значению аргумента 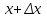 соответствует «наращенное» значение функции соответствует «наращенное» значение функции 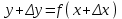 . Соответствующей ему точкой кривой будет точка . Соответствующей ему точкой кривой будет точка  . Проведем секущую . Проведем секущую  и обозначим через и обозначим через 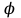 угол, образованный секущей с положительным направлением оси угол, образованный секущей с положительным направлением оси 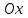 . Составим отношение . Составим отношение 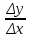 . Из рисунка 2 непосредственно усматриваем, что . Из рисунка 2 непосредственно усматриваем, что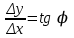 . .Если теперь 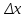 будет стремиться к нулю, то точка будет стремиться к нулю, то точка  перемещаться вдоль кривой, приближаясь к перемещаться вдоль кривой, приближаясь к 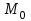 . Секущая . Секущая  будет поворачиваться вокруг точки будет поворачиваться вокруг точки 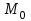 и угол и угол 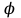 будет меняться с изменением будет меняться с изменением 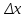 . Если при . Если при 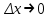 угол угол 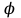 стремиться к некоторому пределу стремиться к некоторому пределу  , то прямая, проходящая через , то прямая, проходящая через 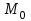 и составляющая с положительным направлением оси абсцисс угол и составляющая с положительным направлением оси абсцисс угол  , будет искомой касательной. Нетрудно найти ее угловой коэффициент: , будет искомой касательной. Нетрудно найти ее угловой коэффициент: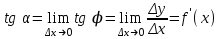 . .Следовательно, 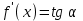 , ,т.е. значение производной 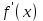 при данном значении аргумента при данном значении аргумента 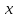 равняется тангенсу угла, образованного с положительным направлением оси равняется тангенсу угла, образованного с положительным направлением оси 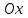 касательной к графику функции касательной к графику функции  в соответствующей точке в соответствующей точке 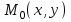 . .Физический смысл производной заключается в скорости изменения функции. Пусть s = s(t) — закон прямолинейного движения. Тогда v(t0) = s'(t0) выражает мгновенную скорость движения в момент времени t0. Вторая производная a(t0) = s''(t0) выражает мгновенное ускорение в момент времени t0.Вообще производная функции y = f(x) в точке x0 выражает скорость изменения функции в точке x0, то есть скорость протекания процесса, описанного зависимостью y = f(x). [4, 680c] 1.3 Понятие дифференциала функции Пусть функция fдифференцируема в точке x, т.е. пусть ее приращение может быть записано в виде  , ,где 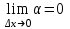 . Это приращение состоит из двух слагаемых: . Это приращение состоит из двух слагаемых: 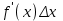 , пропорционального , пропорционального 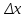 , и , и 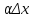 , зависимость которого от , зависимость которого от 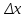 сложнее, так как сложнее, так как  тоже зависит от тоже зависит от 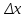 . Слагаемое . Слагаемое 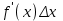 называют дифференциалом функции f и обозначают df, называют дифференциалом функции f и обозначают df, . . Таким образом, дифференциал функции равен произведению ее производной на приращение аргумента. Дифференциал- от латинского слова differentio- разность. Теорема 2. Если функция f дифференцируема в точке x, причем производная от f не обращается в нуль в этой точке, то дифференциал функции f и ее приращение являются при 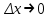 эквивалентными бесконечно малыми, т.е. эквивалентными бесконечно малыми, т.е.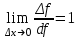 . .Доказательство. Мы имеем  и и  . Так как . Так как 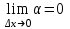 , то , то . .Поскольку дифференциал эквивалентен при 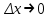 приращению функции, причем он в отличие от приращения пропорционален (а не только «почти пропорционален») приращению аргумента, то дифференциал функции является главной линейной частью приращения. приращению функции, причем он в отличие от приращения пропорционален (а не только «почти пропорционален») приращению аргумента, то дифференциал функции является главной линейной частью приращения.Заметим, что 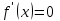 , то дифференциал функции fв точке , то дифференциал функции fв точке 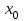 равен нулю. В этом случае равен нулю. В этом случае 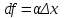 и поэтому приращение является бесконечно малой более высокого порядка, чем и поэтому приращение является бесконечно малой более высокого порядка, чем 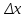 : :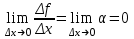 . .Заметим, что дифференциал может быть и больше, чем приращение функции (это будет иметь место, если 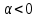 ). ). Пример 1. Найдем приращение и дифференциал функции 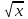 при x=1, при x=1, 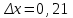 . .Решение. Так как 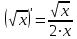 , то , то  . .При 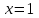 , , 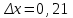 имеем имеем 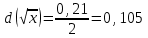 . .Приращение же функции 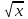 при x=1, при x=1, 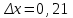 равно равно 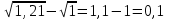 . .Найдем дифференциал для функции f, где f(x)=x. Так как 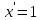 , то , то 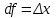 . Поскольку для этой функции f(x)=x, то пишут . Поскольку для этой функции f(x)=x, то пишут 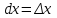 . Таким образом, считают дифференциал независимой переменной равным приращению этой переменной. В соответствии с этим формулу обычно записывают в следующем виде: . Таким образом, считают дифференциал независимой переменной равным приращению этой переменной. В соответствии с этим формулу обычно записывают в следующем виде:  . В приложениях функции обычно записывают в виде . В приложениях функции обычно записывают в виде  , обозначая буквой x аргумент, а буквой y- значение функции. При такой записи производную от функции f обозначают , обозначая буквой x аргумент, а буквой y- значение функции. При такой записи производную от функции f обозначают  или или 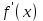 . Соответственно дифференциал функции y=f(x) обозначают . Соответственно дифференциал функции y=f(x) обозначают 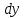 , причем употребляют как запись , причем употребляют как запись  , так и запись , так и запись 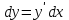 . .Из формулы  следует, что следует, что 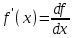 . .Запись  (или (или  ) используется для обозначения производной функции f.[2, 416c] ) используется для обозначения производной функции f.[2, 416c]ГЛАВА 2. ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ К РЕШЕНИЮ ЗАДАЧ 2.1. Исследование функций и построение их графиков Пример 2. Исследовать и построить график функции  Решение. Функция существует для всех 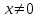 . .Функция не является ни четной, ни нечетной, так как  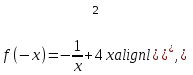 то есть  и и 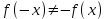 . .В точке х=0 функция имеет разрыв в точке х=0. При этом  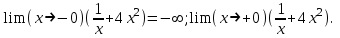 Находим производную: 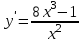 и приравниваем ее к нулю: и приравниваем ее к нулю: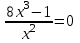 . Точка . Точка 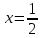 будет критической. будет критической.Проверим достаточные условия экстремума в точке 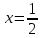 . Так как знаменатель производной всегда положителен, то достаточно проследить за знаком числителя. Получаем: . Так как знаменатель производной всегда положителен, то достаточно проследить за знаком числителя. Получаем: 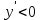 при при 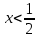 и и 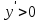 при при 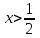 . Следовательно, в точке . Следовательно, в точке 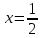 функция имеет минимум, ее значение в точке функция имеет минимум, ее значение в точке 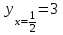 . .Точек пересечения с осью ОY нет, так как данная функция не определена при х=0. Чтобы найти точки пересечения кривой с осью ОХ, нужно решить уравнение 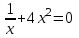 . .Тогда  или или  . .Получим, что при  функция убывает; х= функция убывает; х= y=0; y=0;  функция убывает; при функция убывает; при  функция убывает; при х= функция убывает; при х= функция имеет минимум y=3; при функция имеет минимум y=3; при  функция возрастает. функция возрастает.График данной функции представлен на рисунке.  Кривая, рассмотренная в этой задаче называется «Трезубец Ньютона». 2.2. Нахождение наибольшего и наименьшего значения функции, решение прикладных задач (задач на оптимум) Пример 3. Из бревна, имеющего радиус R, сделать балку наибольшей прочности. Решение: Составляем функцию, выражающую необходимое условие. В данной задаче высота балки (представляющей собой прямоугольник, вписанный в окружность радиуса R и ширины х), равна  . Поэтому прочность такой балки равна . Поэтому прочность такой балки равна 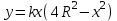 . При этом х изменяется от 0 до 2R. . При этом х изменяется от 0 до 2R.Функция 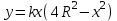 обращается в нуль при х=0 и х=2R и положительна между этими значениями. Значит она имеет максимум, лежащий между 0 и 2R. Но производная этой функции обращается в нуль при х=0 и х=2R и положительна между этими значениями. Значит она имеет максимум, лежащий между 0 и 2R. Но производная этой функции 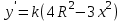 обращается в нуль на отрезке обращается в нуль на отрезке 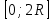 лишь при лишь при  . Это и есть оптимальное значение ширины b балки. Высота h балки такой ширины равна . Это и есть оптимальное значение ширины b балки. Высота h балки такой ширины равна  и отношение и отношение  равно равно  . Именно такое отношение высоты вытесываемой балки к ее ширине предписывается правилами производства строительных работ. . Именно такое отношение высоты вытесываемой балки к ее ширине предписывается правилами производства строительных работ.Пример 4. Требуется построить открытый цилиндрический резервуар вместимостью 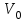 . Материал имеет толщину d. Какими должны быть размеры резервуара (радиус основания и высота), чтобы расход материала был наименьшим? . Материал имеет толщину d. Какими должны быть размеры резервуара (радиус основания и высота), чтобы расход материала был наименьшим?Решение. Радиус основания внутреннего цилиндра обозначим через х, высоту внутреннего цилиндра через h. Объем дна и стенки резервуара  С другой стороны, по условию 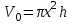 , откуда , откуда  Подставляя в (*), находим  Полученную функцию 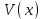 нужно исследовать на экстремум при х>0: нужно исследовать на экстремум при х>0: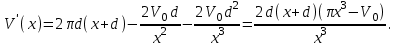 Единственный положительный корень производной – это точка 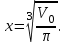 Она и дает решение задачи. При этом Она и дает решение задачи. При этом 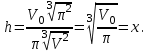 2.3. Определение периода функции Пример 5. Является ли периодической функция 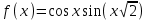 ? ?Решение Воспользуемся следующим утверждением: если дифференцируемая в каждой точке числовой прямой функция имеет период Т, то ее производная также имеет период Т. Предположим, что данная функция  является периодической с периодом Т. Применяя формулу является периодической с периодом Т. Применяя формулу , ,получаем  где где 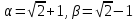 . Имеем . Имеем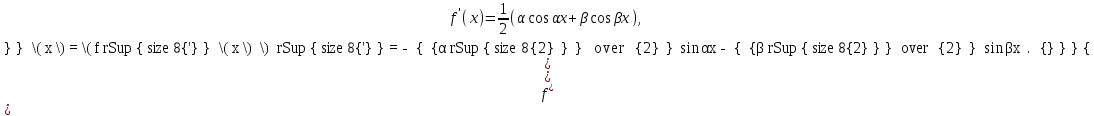 Поскольку по предположению функция  имеет период Т, то функция имеет период Т, то функция 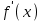 , а следовательно, и функция , а следовательно, и функция 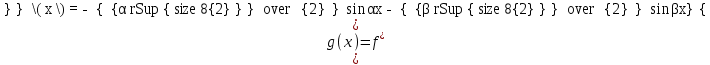 также имеют период Т. также имеют период Т.Значит, и функция 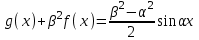 Также имеет период Т. Отсюда следует, что существует число  , , 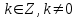 , такое, что Т= , такое, что Т= . Аналогично показывается, что существует число . Аналогично показывается, что существует число 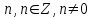 , такое, что Т= , такое, что Т=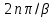 . .Но тогда 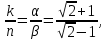 т.е. число 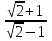 является рациональным, что неверно. Следовательно, данная функция не является периодической. является рациональным, что неверно. Следовательно, данная функция не является периодической.2.4. Нахождение величины угла между прямыми и кривыми. Углом между графиками функций  и и  в точке их пересечения называется угол между касательными к их графикам в этой точке (рис.). в точке их пересечения называется угол между касательными к их графикам в этой точке (рис.).Пример 6. Найти угол между графиками функций  и и  в точке их пересечения (с положительной абсциссой). Решение. Абсциссы точек пересечения данных графиков удовлетворяют уравнению  И тем самым следующей системе: 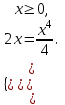 Отсюда находим, что графики функций пересекаются в двух точках, абсциссы которых равны 0 и 2. Найдем тангенсы углов наклона касательных к обоим графикам функций в точке с абсциссой, равной 2. Имеем 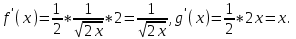 Отсюда 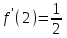 и и  Так как Так как 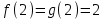 , то уравнения касательных к графикам функций , то уравнения касательных к графикам функций  и и  в точке (2;2) соответственно имеют вид в точке (2;2) соответственно имеют вид и и 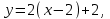 т.е.  и и  Следовательно, величина угла  между касательными удовлетворяют уравнению между касательными удовлетворяют уравнению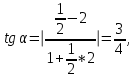 и тем самым графики функций и тем самым графики функций  и и  в точке с абсциссой х=2 пересекаются под углом, равным в точке с абсциссой х=2 пересекаются под углом, равным 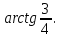 [3, 496 c] [3, 496 c] |
