лекция. СТРЭС -Л 1-4ТВ. Функциональные преобразования случайных величин в задачах анализа рэс
 Скачать 79.69 Kb. Скачать 79.69 Kb.
|
|
ЛЕКЦИЯ 4. ФУНКЦИОНАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ СЛУЧАЙНЫХ ВЕЛИЧИН В ЗАДАЧАХ АНАЛИЗА РЭС 4.1.Плотность вероятности монотонной функции случайного аргумента 4.1.1Функциональное преобразование случайной величины На практике часто одна случайная величина 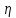 бывает связана с другой бывает связана с другой 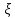 известной функциональной зависимостью известной функциональной зависимостью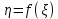 (4.1) (4.1)и требуется найти закон распределения 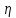 если известно распределение случайного аргумента если известно распределение случайного аргумента 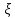 . Выражение (4.1) является расширенным понятием функции на случай, когда аргументом является случайная величина. . Выражение (4.1) является расширенным понятием функции на случай, когда аргументом является случайная величина.Для нахождения 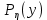 ,если известна ,если известна 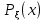 , рассмотрим сначала случай, когда функция , рассмотрим сначала случай, когда функция 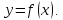 (4.2) (4.2)Связывающая между собой возможные значения x и y соответственно случайные величины 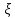 и и 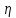 ,является непрерывной монотонной функцией (рис.4.1.а). Это означает, что производная dy/dx не меняет значения между x и y имеется однозначная связь. ,является непрерывной монотонной функцией (рис.4.1.а). Это означает, что производная dy/dx не меняет значения между x и y имеется однозначная связь.    y y    y+dy y+dyy       +dy y +dy y  y y  0 x x+dx x x1 x2 x3 x1+dx1 x2+dx2 x3+dx3 а) б) рис.4.1. Монотонная и немонотонная функциональные зависимости В силу однозначной связи между 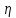 и и 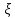 вероятность нахождения вероятность нахождения 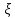 на интервале [х;x+dx]: на интервале [х;x+dx]:P(y< 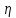 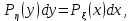 Куда 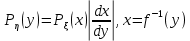 (4.4) (4.4)Абсолютного значения производной [dx/dy] поставлен потому. Что любая плотность вероятности по своему определению не может быть отрицательной, а производная dx/dy может быть и больше, и меньше нуля. Кроме того, чтобы справа была зависимость только от x необхожимо в 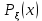 x выразить через y:x= x выразить через y:x=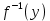 , где , где  функция обратная f. функция обратная f.4.2 .Плотность вероятности немонотонной функции случайного аргумента Если же функция 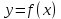 немонотонная (рис.4.1.б), то вероятность нахождения немонотонная (рис.4.1.б), то вероятность нахождения 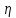 на интервале [ на интервале [ < <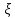 < < +d +d ], или на интервале [ ], или на интервале [ < <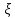 < < +d +d ], или на интервале [ ], или на интервале [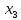 < <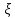 < <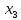 +d +d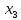 ], но на каком-то одном из них, то есть задача сводится к случаю нахождения вероятности трех несовместных событий. Применяя формулу (7.3) к данному случаю имеем ], но на каком-то одном из них, то есть задача сводится к случаю нахождения вероятности трех несовместных событий. Применяя формулу (7.3) к данному случаю имеемP(y< 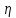  < <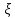 < < +d +d )+( )+( < <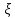 < < +d +d )+( )+(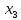 < <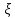 < <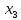 +d +d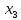 ) )К плотностям вероятности и методика рассмотрения задана в монотонном случае, имеем:  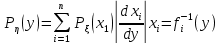 (4.5) (4.5)где формула (4.5) сообщена на случай, когда число неоднозначностей в общем случае будет n. Таким образом, можно сформулировать следующее правило определения 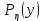 , если известны , если известны 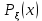 и зависимость у = f(х). и зависимость у = f(х).1. Провести анализ у= f(х), в результате которого определено число неоднозначностей n и найти производные dxi/dy по каждому участку неоднозначности. 2. Воспользоваться формулами (4.4), если n = 1, или (4.5) общем случав и найти 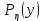 , выразив каждое хi через , выразив каждое хi через 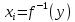 . .3. По заданному интервалу [  ] существования случайной величины ] существования случайной величины 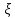 найти интервал [а,b] на основании функциональной зависимости. найти интервал [а,b] на основании функциональной зависимости.4.3.Чиловые характеристики функции случайного аргумента Получив 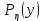 , числовые характеристики , числовые характеристики 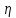 можно определить в можно определить в соответствии с их определением. Например, для математического ожидания я дисперсии имеем выражения: 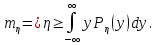 (4.7) (4.7) (4.8) (4.8)Если же в задаче по заданным y=f(x) и 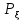 (х) требуется найти только (4.7), (4.8) и не ставится вопрос об определении (х) требуется найти только (4.7), (4.8) и не ставится вопрос об определении 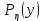 , то в этом случае , то в этом случае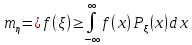 (4.9) (4.9)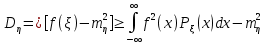 (4.10) (4.10)Другими словами, для определения только 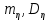 в задачах по диффернециальному преобразованию находить в задачах по диффернециальному преобразованию находить 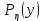 не обязательно. не обязательно.4.4. Функциональное преобразование системы двух случайных величин Пусть двумерная случайная величина ( 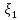 , ,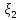 ) функционально ) функциональносвязана с другой двумерной случайной величиной ( 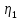 , ,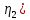 так, что прямые и обратные зависимости их возможных значений (X1,X2 )(У1, так, что прямые и обратные зависимости их возможных значений (X1,X2 )(У1,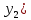 . . Прямые зависимости: 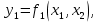 (4.11) 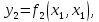 Кратные зависимости: 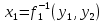 , ,(4.12) 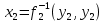 . .Пусть прямые и обратные зависимости являются однозначными, непрерывными и дифференцируемыми. Примерами таких функциональных преобразований служат поворот прямоугольных координат или преобразование прямоугольных координат в полярные и обратно. Поставим задачу найти двумерную плотность вероятности 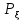 =2(y1,y2)= =2(y1,y2)=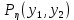 , если известна плотность вероятности аргументов , если известна плотность вероятности аргументов  = = 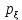 (x1,x2) и заданы функциональные зависимости (x1,x2) и заданы функциональные зависимости(7.11),(7.12). Применив методику, изложенную выше, получим Р(У1< 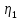 <У1+dy1;У2< <У1+dy1;У2<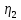 <У2+dy2)=P(x1< <У2+dy2)=P(x1<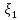 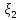 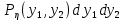 = =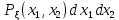 , ,откуда 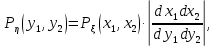 где знак абсолютного значения поставлен из соображения объяснения условия 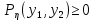 . .Из математического анализа известно, что соотношение I J2= 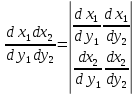 является якобианом преобразования, который выражается через делитель второго порядка. Таким образом, 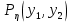 = = 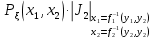 то есть плотность вероятности 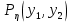 при функциональном преобразовании определяется произведением двумерной плотности вероятности аргументов на абсолютное значение якобиана преобразования при выражении аргументов через функции. при функциональном преобразовании определяется произведением двумерной плотности вероятности аргументов на абсолютное значение якобиана преобразования при выражении аргументов через функции.4.5. Двумерная плотность вероятности модуля и аргумента случайного вектора при гауссовских проекциях. (пример) Рассмотрим случайный вектор, у которого проекции в прямоугольной системе координат являются случайными величинами 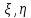 . Поставим задачу найти двумерную плотность вероятности модуля А и аргумента (т.е. фазы) Ф этого случайного вектора в случае если . Поставим задачу найти двумерную плотность вероятности модуля А и аргумента (т.е. фазы) Ф этого случайного вектора в случае если 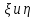 являются независимыми гауссовскими случайными величинами при являются независимыми гауссовскими случайными величинами при 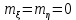 и при одинаковых дисперсиях и при одинаковых дисперсиях 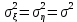 , так что двумерная плотность вероятности определяется выражением (6.43). , так что двумерная плотность вероятности определяется выражением (6.43).По своему геометрическому смыслу поставленная задача сводится к определению плотности вероятности полярных координат случайной точки, если её прямоугольные координаты являются независимыми величинами. Прямые и обратные зависимости между возможными значениями координат а, 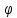 и прямоугольных координат х, у (рис.7.1) определяются следующими выражениями. и прямоугольных координат х, у (рис.7.1) определяются следующими выражениями.а= 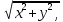 где а где а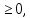 (7.17) 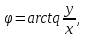 где –x< где –x<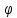 обратные: х=асоs 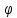 y=asin y=asin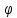 (7.18) (7.18)Воспользуемся формулой(7.16), которая для данного случая представляется в виде P(a, 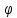 )=p(x,y) )=p(x,y)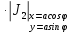 (7.19) (7.19) p(a) p(a)    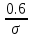    y а y а   x x a) 0 a) 0 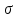 ma a ma ap( 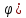  б) б)       - 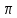 0 0 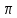 в) Якобиан преобразования будет равен 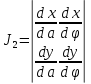 = = =a =a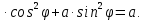 (7.20) (7.20) Подставив (7.20) в (7.19), получим P(а, 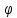 )= )=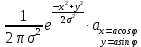 = = , (7.21) , (7.21) где а 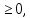 – –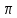 < <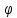 < <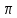 \'7.24> \'7.24>Формула (7.21) определяет искомую двумерную плотность вероятности модуля и фазы случайного вектора при гауссовских проекциях с нулевым математическим ожиданием и одинаковыми дисперсиями. Для нахождения отдельно р(а) или р( 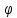 ) нужно проинтегрировать р(а, ) нужно проинтегрировать р(а,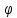 ) по всем возможным значениям ) по всем возможным значениям 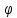 или а (лекция 6). Тогда или а (лекция 6). Тогда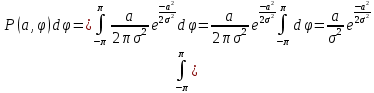 (7.22) (7.22) Полученная зависимость р(а) носит название распределения (рис.7.2.б). Говорят, что длина вектора при рассмотрении в гауссовских проекциях с нулевым средним и одинаковыми дисперсиями имеет распределение Релея, в котором параметр 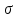 играет роль моды, а математическое ожидание и дисперсия соответсвенно медианы: играет роль моды, а математическое ожидание и дисперсия соответсвенно медианы: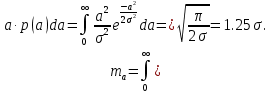 (7.23) (7.23)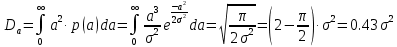 (7.24) (7.24)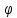 в свою очередь в свою очередь р( 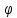 )= )=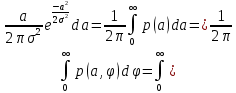 (7.25) (7.25)так как 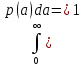 по условию нормировки. по условию нормировки. Из (7.25) следует что р( 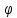 ) не зависит от ) не зависит от 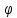 и имеет постоянное значение и имеет постоянное значение 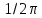 на интервале от на интервале от 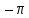 до до 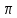 . Говорят, что фаза или аргумент вектора имеет равномерное распределение, так что согласно (5.23) и (5.24) лекции 5, имеем . Говорят, что фаза или аргумент вектора имеет равномерное распределение, так что согласно (5.23) и (5.24) лекции 5, имеем 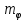 = =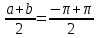 =0 =0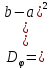 = =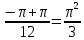 Полученный результат имеет радиотехническую интерпретацию. Любой узкополосный процесс может быть представлен вектором, которого модуль соответствует амплитуде (огибающей), a аргументом в фазе колебаний. Если ортогональные составляющие этого узкополосного процесса независимы и имеют гауссовское распределение с левыми математическими ожиданиями и одинаковыми дисперсиями, огибающая процесса имеет релеевское распределение, а фаза распределяется равномерно на интервале [ 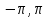 ]. ].ЗАКЛЮЧЕНИЕ В лекции выведены соотношения для плотности вероятности числовых характеристик случайной величины и системы двух случайных величин, полученных в результате функционального, в общем случае нелинейного, преобразования. Приведены примеры преобразований системы случайных величин при переходе от прямоугольной полярной системы координат и при суммировании случайных величин. Раскрыта методика моделирования на ЭВМ случайной величины, имеющий заданный закон распределения. |
